ГРАФТАР ТЕОРИЯСЫНЫҢ ЭЛЕМЕНТТЕРІ

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 53 бет
Таңдаулыға:

МАЗМҰНЫ

КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..3
1 ГРАФТАР ТЕОРИЯСЫНЫҢ ЭЛЕМЕНТТЕРІ ... ... ... ... ... ... ... ... ... ... ... ...8
0.1 Графтар теориясының негізгі ұғымдары және анықтамалары ... ... ... ... ... ... ..8
0.2 Графтардың берілу тәсілдері, сандық сипаттамалары ... ... ... ... ... .. ... ... ... .14
0.3 Эйлерлік және гамильтондық графтар ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..1 8
1.4 Графтардағы қысқа жолды табу. Дейкстр алгоритмі ... ... ... ... ... ... .. ... ... ... 28
2 ҚОЛДАНБАЛЫ ЕСЕПТЕРДІ ШЕШУДЕ ГРАФТАРДЫ ҚОЛДАНУ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...33
2.1 Коммивояжер есебін Тармақ және шекара әдісімен шешу ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..33
2.2 Желілік қойылымдағы көлік есебін шешу. Потенциалдар әдісі ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 35
2.3 Желілік жоспарлауда графтардың қолданылуы ... ... ... ... ... ... . ... ... ... ... ... .41
2.4 Графтар қолданылып шығарылатын экономикалық есептер ... ... ... ... ... . 41
ҚОРЫТЫНДЫ ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...62
ҚОЛДАНЫЛҒАН ДЕРЕКТЕР ТІЗІМІ ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... .64

КІРІСПЕ

Графтар теориясы XVIII ғасырдың 30-шы жылдарының ортасында математиканың өз алдына бір саласы ретінде басталып, осы уақытқа дейін қарқынды дамып келе жатқан ғылым.
Графтар теориясы объектілерді реттеудің моделін құрып, әр түрлі саладағы есептерді жалпылау және шешімін табуда қолданылатын қарапайым, тиімді және қуатты құрал болып табылады. Жеке жағдайда, мұндай есептерге байланыс желілерін зерттеу және жобалау, электрлік желілерді талдау, баспа схемаларын талдау, электрлік және монтаждау схемаларын жобалау есептері, бағдарламалардың блок-схемалары, автоматтарды зерттеу, календарлық жоспарлау есептері, материалдық-техникалық жабдықтауды қамтамасыз ету және жоспарлау, ақпараттарды іздеу, ақпараттар теориясы, коммуналдық қызмет көрсету мекемелерін орналастыру, ойындар теориясы, биология, генеалогия, бас қатырғыш ойындар, заттың химиялық құрамын анықтау, экономикалық есептердің алуан түрлері және басқалар жатады.
Графтар теориясының табиғаты жағынан әртүрлі күрделі жүйелерді талдау және жобалау жұмыстарындағы кең түрде қолданылулары оның жедел түрде дамуына жол ашып отыр.
Қарапайым тілмен айтқанда, граф дегеніміз нүктелер (төбелер) және оларды қосатын сызық кесінділерінің (қабырғалардың) жиыны.
Немесе, берілген нүктелерді бір-бірімен қосатын сызықтар тобы граф деп аталады. Берілген нүктелерді графтың төбелері дейді де, төбелерді екі-екіден қосатын сызықтарды графтың қабырғалары дейді. Қабырға немесе қыр түзу де, қисық сызық та болуы мүмкін. Мысалы, Алматы, Көкшетау, Семей, Талдықорған қалаларын алайық, оларды қысқаша А, К, С, Т әріптерімен белгілейік. Сонда Алматы-Семей жолы АС, Көкшетау-Талдықорған жолы КТ,..., т.с.с. болады (темір жол, қара жол, су жолы, әуе жолы-бәрібір). Бұл жолдардың схемасы граф құрастырады, схемадағы А, К, С, Т нүктелері графтың төбелері АС, АК, ... , СТ сызықтары графтың қабырғалары рөлін атқарады. Мұндай графтың төбелері үшінші дәрежелі болады. Төбелері сызықтар арқылы қосылмаған толымсыз графтар да кездеседі. Оларды жетпей тұрған қабырғаларын сызып, толықтыруға болады.
Төбелері бір жазықтықта жататын графтар жазық графтар болып табылады, төбелері бір жазықтықта жатпайтын графтар кеңістік графтары болады.
Кеңістік графтарын жазық графтарға жіктеуге болады. Әдетте жазық графтар қабырғалары төбелерде ғана қиылысатындай етіліп сызылады. Графтардың алдын-ала берілген шарттарды қанағаттандыратын арнайы түрлері де бар. Мысалы, бағдарлы графтарда қабырғаларының бағдары - төбелерден өту реті бойынша айтылады, қабырғаларының салмағы бар графтарда тиісті қабырғаларының ұзындығы, өткізу қабілеті т.с.с. көрсетіледі. Кейбір қабырғалары бірнеше рет есептелетін (еселі қабырғалар), кейбір төбелері айрықша рөл атқаратын (полюстер) графтар да қарастырылады.
Граф ұғымының орнына "желі" ұғымы жиі қолданылады.
Бұл әсіресе графтағы негізгі таза құрылымдық қатынастардан басқа графты құрайтын нүктелер мен сызықтардың кейбір сандық сипаттамалары берілген жағдайға байланысты. Мысал ретінде, электр желісі, жобадағы жұмыстарды орындау желісі т.б.
Мұнда желі қабырғаларына энергия, шығын және ағынның анықталған сандық сипаттамалары сәйкестікке қойылады. Мұндай қолданылулардың негізгі мақсаты ғылыми және техникалық есептерді графтар теориясы тілінде тиімді жаза білу және есептерді тұжырымдамасы мен шығарылу барысындағы графтарды қолданудың әртүрлі тәсілдерін білу.
Күрделі комплексті жұмыстар моделі біздің ғасырымыздың 50-ші жылдарында жинақталып іске қосылып, қолданыла бастады. Америкада желілік модель американ әскери-теңіз флотының су асты қайықтарына жарық беріп тұратын "Поларис" деп аталатын баллистикалық ракетаны жасау барысында қолданылды. Жұмыс Американың 48 штатында 6000 фирманың қатысуымен орындалды, желілік график құрамында 10000 оқиға болды. АҚШ-та желілік жоспарлау және басқару әдісі кең қолданылады, алғаш шыққан және кең қолданыс тапқан басқару жүйесі "ПЕРТ" деп аталады. "ПЕРТ" жүйесін игермеген бірде-бір фирма контракт ала алмайтын болған. Америкалық экономистер пікірінше графтар теориясын қолдана отырып құрылған желілік модельдеу жұмыстар комплексінің орындалу ұзақтығын үш есеге дейін қысқартуға мүмкіндік береді.
Біздің елімізде желілік жоспарлау және басқару деп аталатын бірнеше жүйе бар. Бұл жүйелер негізі де желілік график болып табылады. ЖЖБ көмегімен ТМД елдеріндегі ірі-ірі құрылыс жұмыстары, алып заводтар, ЖЭЦ т.б. салынды. Қазіргі жағдайда да мекемелер, құрылыс фирмалары, ғылыми зерттеу, жобалау институттары т.б. осы жүйе бойынша жұмыс жасайды. Желілік графиктің немесе оның бөліктерінің көрнектілігі жалпы жүйенің болмысын, барлық жұмыстардың бір-бірімен байланысын қабылдауды жеңілдетеді, жобаны іске асыру барысындағы жұмыстар процесін қысқартуға көмектеседі.
Бұл зерттеу жұмысында қарастырылатын графтардағы экстремалды есептерді шешу әдістері графтар теориясының негізгі классикалық есептерінің бірі болып табылады. Графтардағы экстремалды есептер дегеніміз - желіде қандай да бір граф арқылы берілген сандық функцияның ізделінді ең үлкен немесе ең кіші мәнін табу есептері болып табылады. Мұндай есептерге қысқа жолды іздеу есептері, тағайындау есептері, коммивояжер есебі, желідегі максимал ағынды есептеу, тұйық сызықты ажырату есебі секілді есептерді жатқызуға болады.
Бүгінде бұл есептерді шешудің көптеген алгоритмдері белгілі.
Мұндай мағынадағы есептер олардың әртүрлі практикалық мақсаттарда қолданылуларымен маңызды. Мысалы, қандай да бір екі қиылыс арасындағы қысқа жолды іздеу орындалатын GPS-навигаторларда, граф төбелері ретінде қиылыстар, ал жолдар олардың арасында жатқан қабырғалар орнында болады. Қиылыстардың арасындағы барлық жолдардың қосындысы ең аз болу керек, сонда ғана қысқа жол табылды деп есептеледі.
Графтағы экстремалды есептер бағытталған, бағытталмаған немесе аралас графтар үшін анықталуы мүмкін. Жұмыста қарапайым түрде бағытталмаған граф үшін есептің қойылуы қарастырылады.
Зерттеу жұмысы тақырыбының өзектілігі - жұмыста негізі қарапайым идеялар мен элементтер: нүкте, оларды қосатын сызықтар бола тұрып, олардан көлемді, күрделі формалар тұрғызып және ол формаларды қызықты қасиеттері бар формаға, күрделі жобаға айналдыратын графтар теориясының жұмыс принциптеріне түсінік беріледі, бұл теория өз алдына жеке теория болғанымен ғылым мен математиканың басқа салаларымен тығыз байланыста екендігі, қоғам мүшелерінің күнделікті жұмыс жоспарларын, жалпы өмірлік идеясын құру, іске асыру барысында осы теория элементтерін қолдануға болатындығы көрсетіледі. Компьютерлік жүйелерді, телефон байланысын, тұрбалар жүргізу және жол құрылысын жобалау т.б. жұмыстарында шығынды, жұмсалатын қаржыны минималдау қажеттілігі туындайды. Осыған байланысты аз ұзындықтағы маршрутты, жолды анықтау есебі туындайды. Бұл есеп қай кезде де өзекті мәселе болып табылады және оны шешуде әртүрлі әдістер қолданылады. Жұмыста графтардағы экстремалды есептердің қойылуы, есептердің оңтайлы шешімдерін табудың Дейкстр (2), Форд-Фалкерсон, Литлл алгоритмдері баяндалып, оларды практикада қолданылуы есептер көмегімен түсіндіріледі.
Графтар теориясын олардың негізгі ұғымдары мен анықтамаларын, геометриялық кескінделуін, графтарды беруде қолданылатын матрицаларды, графтардың қасиеттерін білмей, қолданылу жағдайларын қарастырмай оқып-үйрену мүмкін емес. Сондықтан да диссертация жұмысы барысында жүргізілген зерттеу мақсаты - графтар теориясының негізгі ұғымдарын, анықтамалары мен теоремаларын талдап, зерттей келе қолданалы есептерді шешуде графтардың қолданылуымен, графтар теориясының әдістерімен танысу және оларды практикада қолдана білу болып табылады. Сонымен қатар, графтар теориясында қолданылатын матрицалар түрлеріне түсінік беру, графтарды ЭЕМ-да беруге қолайлы болатын матрицалар түрінде кескіндеу болып табылады.
Диссертация жұмысының зерттеу пәні және нысаны - соңғы жылдарда қарқынды дамып, математикалық кибернетиканың негізіне айналған, қолданбалы математиканың бөлімі болып табылатын дискретті математика пәнінің нысандарының бірі - графтар теориясының негізгі ұғымы - граф, графтардағы ара қашықтық, қысқа жол, оны іздеу есебі, коммивояжер есебінің оңтайлы шешімдерін табу жолдары, транспорттық есептердегі максимал ағындарды есептеу мәселелері болып табылады.
Зерттеу міндеттері:
а) Дискретті математика пәні және оның бөлімдерімен танысу;
ә) Графтар теориясының негізгі нысаны, анықтама, теоремаларымен, пайда болу тарихымен танысу, оқып-үйрену;
б) Графтартың қолданбалы есептерді шешуде қолданылу әдістерімен танысу және оларды практикада қолдана білу.
Зерттеудің әдістемелік негізіне Қазақстан Республикасындағы 2011-2020 жылдарға арналған білім беруді дамытудың мемлекеттік бағдарламасы, қазіргі кезеңдегі оқыту әдістемесі және математика ғылымдарының жетістіктері, дидактиканың оқыту ұстанымдары, отандық және шетелдік математик ғалымдардың оқыту нәтижесінде білім алушының ақыл-ой, танымдық қабілеттерін дамыту туралы іргелі теориялық қағидалары, мамандыққа сәйкес білім берудің мемлекеттік стандарты, бағдарламалар, оқулықтар, оқу құралдары, оқытудың жаңа технологиялары туралы ғылыми-әдістемелік еңбектер негіз болды.
Зерттеудің теориялық негіздерін шетелдік және отандық Джеймс Андерсон, Судоплатов С.В., Овчиникова Е.В., Нефедов В.Н., Осипова В.А., Горбатов В.А., Березина Л.Ю., Джумадильдаев А.С., Қ. Жетпісов., Г. И. Салғараева., Алексеев В.Е., Таланов В.А. тәрізді белгілі ғалымдардың дискретті математика, графтар теориясы саласындағы еңбектері құрайды.
Мәселенің зерттелу деңгейі - графтар теориясының математикалық пән болып қалыптасуы Эйлердің 1736 жылғы Кенигсберг көпірлері туралы әйгілі тұжырымдамасынан бастау алған, алайда бұл мақала одан кейінгі жүз жыл бойына жалғыз ғана мақала болып есептелді. Графтар теориясы өткен ғасырдың орта шамасында жаратылыстану ғылымдарының (физика, электротехника, химия, биология) және бас қатыру ойындары әсерінен Англияда қайта жаңғырды. Олардың ішіндегі ең маңыздысы 1850 жылдары де-Морганның графтарды бояу, төрт бояу есебі. Соңғы кезде графтар теориясы білім-ғылымның әртүрлі саласы мамандарының қызығушылығын туындатып отыр. Графтардың дәстүрлі физика, химия, биология саласындағы қолданылуларымен қатар, оның экономикада, әлеуметтануда, лингвистикада, топологияда, топтар теориясында, ықтималдықтар теориясында, психологияда да қолданылатындығы белгілі болды. Графтар теориясы элементтері мен қазіргі уақытта қарқынды дамып отырған теориялық кибернетика (автоматтар теориясы, амалдарды зерттеу, кодтау теориясы, ойындар теориясы, бағдарламалау) арасындағы байланыс өте маңызды орын алады.
Графтар теориясының, жалпы дискретті математика курсының негізін қалаған, қазіргі дискретті математика саласына қомақты үлес қосқан ағылшын математигі, философ Б.Рассел, ағылшын математигі А.Тьюринг, америкалық математиктер А.Чёрч, К.Гёдель, Э.Пост, С.Клини, Дж.Андерсон, польшалық математиктер Л.Лукасевич, С.Мостовской, совет математиктері А.А.Марков, И.И.Жегалкин, П.С.Новиков, В.М.Глушков, Нефедов В.Н., Осипова В.А. ресейлік ғалымдар С.В.Яблонский, О.Б.Лупанов, Ю.И.Журавлев, О.Оре, О.И. Мельников есімдерін атауға болады.
Зерттеу әдістері. Жұмыс тақырыбына сәйкес жүргізілген зерттеу барысында ғылыми және әдістемелік әдебиеттерді талдау, баяндау, жүйелеу, талдау, салыстыру, тұжырымдау, минимальдау, зерттеу нәтижелерін қорытындылау, мәліметтерді сапалық және сандық тұрғыда сараптау, жинақтау әдістері қолданылды.
Ғылыми жаңашылдығы. Студенттердің дүниетанымын кеңейтуге, логикалық ойлау мәдениетін дамытуға игі әсер ететін дискретті математиканың және оның негізгі тарауларының бірі графтар теориясының негізгі анықтама, теоремалары, қазіргі замандағы қолданылу жағдайлары, графтар теориясының қолданбалы есептерді шешуде қолданылуы көрсетілді, қысқа жолды іздеуде Дейкстр алгоритмі, коммивояжер есебін шешуде, желілік жоспарлауда, көлік есебін шешуде графтардың қолданылуы көрсетілді.
Диссертация жұмысының теориялық маңыздылығы - теориялық кибернетика саласы бойынша білім алушылар мен мамандар үшін графтар теориясының маңызды мәселелерінің бірі болатын графтардағы экcтремалды есептердің қойылуымен, есептің теориялық және практикалық тұрғыдан жүйелі түрде баяндалуымен анықталады.
Диссертация жұмысының практикалық маңыздылығы - графтар теориясы программалау теориясында, есептегіш машиналар жасауда, физикалық, химиялық және технологиялық процестерді зерттеуде, лингвистикада, халық шаруашылығын жоспарлау сияқты алуан түрлі жұмыстарда қолданылады. Олай болса, әрбір жас заман ағымына сай жан-жақты дамыған, білімді, білікті азамат боламын десе, қарапайым идеялар негізінде үлкен игі істерге бастайтын графтар теориясынан және оның негізгі классикалық есептерінің бірі болып табылатын графтардағы экстремалды есептердің қойылу жағдайларынан, қолданбалы есептерді шешуде графтардың қолданылуынан , сонымен қатар олардың қолданбалы мүмкіндігінен хабары болғаны дұрыс.
Диссертация жұмысының құрылымы. Жұмыс кіріспеден, 2 бөлімнен, қорытынды және пайдаланылған деректер тізімінен тұрады.

1 ГРАФТАР ТЕОРИЯСЫНЫҢ ЭЛЕМЕНТТЕРІ

3.1 Графтар теориясының негізгі ұғымдары және анықтамалары

Ресейдің батысында Калининград қаласы бар, бұрын ол Кенигсберг деп аталды. Қала арқылы Преголь өзені ағып өтеді. Ол екі жеңге бөлінеді және аралды айналып өтеді. XVIII ғасырда қалада 1-суретте көрсетілгендей орналасқан жеті көпір болды.

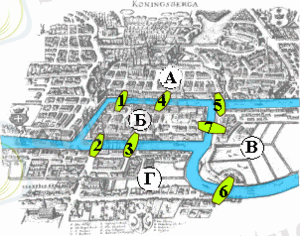
1-сурет. Кеннигсберг

Бір күні қала тұрғыны өзінің танысынан барлық көпірлерден олардың әрқайсысында тек бір рет болып, серуендеу басталған жерге оралатындай етіп өте алады ма деп сұрады. Көптеген қалалықтар бұл міндетті қызықтырды, алайда ешкім шешім қабылдай алмады. Бұл мәселе түрлі ел ғалымдарының назарын аударды. Бұл мәселені белгілі математик Леонард Эйлер шешеді. Сонымен қатар, ол осы нақты міндетті шешіп қана қоймай, сондай-ақ осындай міндеттерді шешудің жалпы әдісін ойлап тапты. Сондықтан графтар теориясының негізін қалаушы Леонард Эйлер деп саналады.
Көптеген қолданбалы есептерде түрлі объектілер арасындағы байланыс жүйелері зерттеледі. Объектілер төбелер деп аталады және нүктелер немесе дөңгелекшелермен белгіленеді, ал төбелер арасындағы байланыстар нүктелердің жұптарын қосатын кесінділермен белгіленеді; және бұл кесінділер қабырғалар деп аталады. Мұндай жүйелерді қарастыру граф ұғымына әкеледі.
V- бос емес жиын, 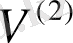- осы жиынның екі элементтен тұратын барлық ішкі жиыны, яғни, 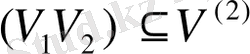, егер 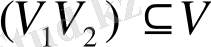болсын.
Анықтама. G= 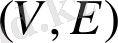жұбы бағытталмаған граф ( немесе граф) деп аталады. Мұндағы .
V жиынының элементтері графтың төбелері деп аталады, ал E жиынының элементтері графтың қабырғалары деп аталады.
Графтардың E,V әріптермен белгілену себебі ағылшын сөздерінің бас әріптерінен алынған. Яғни vertex- төбе, edge- қабырға деген мағыналарды білдіреді екен.
1-мысал. Келесі графты қарастырайық.

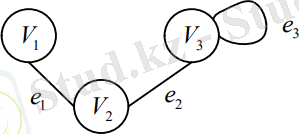
1-сурет. Графтың мысалы

Мұндағы төбелер жиыны болады, ал қабырғалар жиыны 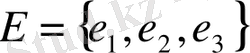болады. Мұнда

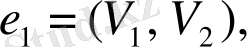
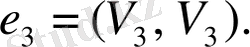
Анықтама. Егер е қабырғасы 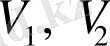төбелерін қосатын болса, яғни 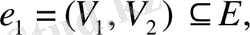онда 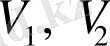төбелері іргелес деп аталады, ал 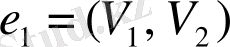қабарғасы 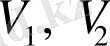төбелеріне инцидентті деп аталады.

Анықтама. Егер V және E жиындары ақырлы болса, онда G ақырлы граф деп аталады.
Егер е қабырғасы 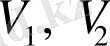төбелеріне инцидентті болса, онда мұндай төбелер е қабырғасының шекаралық нүктелері деп аталады.
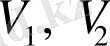Егер төбелері е қабырғасына инцидентті болса және 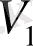төбесі 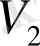төбесінмен беттессе, яғни қабырғаның басы мен соңы бір төбеде орналасса, онда е қабырғасы ілмек деп аталады. Бұл жағдайда төбесі өз-өзіне ірелес болып табылады. 1-суреттегі 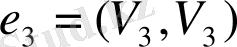қабырғасы ілмекке мысал болады.
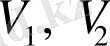төбелері біруақытта 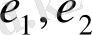қабырғаларына инцидентті болса, онда 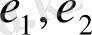қабырғалары параллель қабырғалар деп аталады.
Егер 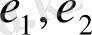қабырғаларының ең болмағанда бір шекаралық нүктесі болса, онда 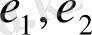қабырғалары іргелес деп аталады.
Іргелестік - екі ұқсас элементтің арсындағы қатынас ( төбелер арасындағы немес қабырғалар арасындағы) болып табылады. Инциденттік - әртүрлі элемент арасындағы қатынасты қатынасты көрсетеді.
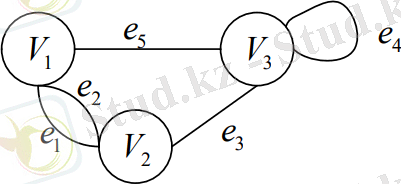
2-мысал. Келесі графты қарастырайық.

2-сурет.

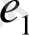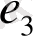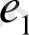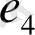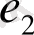Суреттегі графта көріп отырғанымыздай, және қабырғалары параллель болады, және қабырғалары сыбайлас болып табылады. және , және 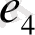сыбайлас қабырғалар бола алмайды, 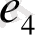қабырғалы ілмек болып табылады.
Анықтама. V төбесіне инцидентті қабырғалар саны (ілмек екі рет есептеледі) V төбесінің дәрежесі деп аталады және деп белгіленеді. Егер болса, V төбесі оқшауланған болып саналады. Егер қабарға ілмек болатын болса, онда 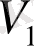төбесінің дәрежесі 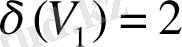болады.
3-мысал. Граф төбелерінің дәрежелерін табайық.

3- сурет.

,

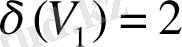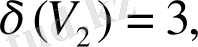
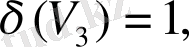
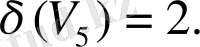
Анықтама. Графтың барлық төбесі оқшауланған болса, онда граф ерекше (бос) деп аталады.
4 - мысал. Ерекше графқа мысал қарастырайық.

4 - сурет. Ерекше граф.

G=(V, E) және 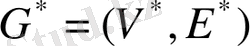графтарды қарастырайық және 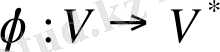биекциясы ( өзара бірмәнді бейнелеу) бар болсын.
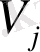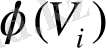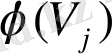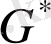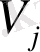Анықтама. Егер G графының кез-келген және төбелері үшін олардың және бейнелері графында сыбайлас болады, сонда, тек сонда ғана және төбелері G графында сыбайлас болса. Бұл биекция G графының графы үшін изорморфизмі деп аталады. Егер осындай биекция бар болатын болса, онда G графы графына изоморфты болады.
5 - мысал. Изоморфты графтарға мысал келтірейік.

5 - сурет. Изоморфты графтар

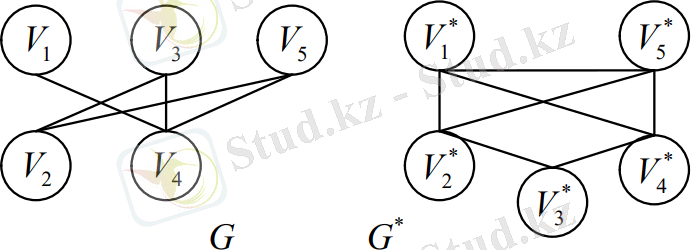
6 - сурет. Изоморфты емес графтар.

G және 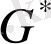графтарындағы төбелер саны бірдей, бірақ төбелердің дәрежелері әртүрлі. Мысалы, G графындағы 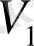төбесінің дәрежесі бірге тең. 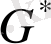графында дәрежесі екіден кем болатын төбе жоқ.
Теорема. Ақырлы графта тақ дәрежелі төбелердің саны жұп болады.
Дәлелдеу. Егер төбе тақ дәрежелі болатын болса, оған инцидентті қабырғалар саны тақ дегенді бәлдіреді. Графтардағы осындай төбелердің саны жұп болатындығын дәлелдейік.
G=(V, E) ақырлы графты қарастырайық. және сәйкесінше төбелердің және қабырғалардың саны болсын.
- таңбасы жиынның қуатын білдіреді, яғни жиындағы элементтер санын білдіреді.
Тұжырым:
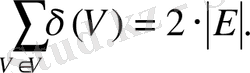
V төбелер жиынын екі жиынға бөлейік:
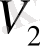- жұп дәрежелі төбелердің жиыны, 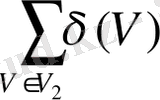- дәрежелері жұп болатын төбелердің дәрежелерінің қосындысы.
- тақ дәрежелі төбелердің жиыны, - дәрежелері тақ болатын төбелердің дәрежелерінің қосындысы.

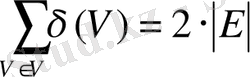тұжырымы бойындша, бұл қосынды жұп болады. 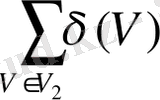қосындысы да жұп болады.
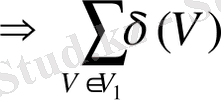- жұп сандардың қосындысы жұп болғандықтан, қосынды жұп болады.
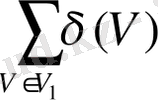қосындысында тақ сандар бір-біріне қосылады. 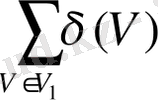қосындысы жұп болу үшін қосылғыштардың саны жұп болу керек. Дәрежесі тақ болатын төелердің саны жұп болады.
Анықтама. Кез келген екі төбесі сыбайлас болатын графты толық граф (ілмексіз) деп атайды. n төбеден тұратын толық графтың 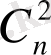қабырғасы болады.
Комбинаторикада - n элементтен k терулер санын білдіреді. Терулер саны келесі формуламен анықталады:
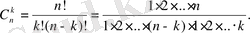Cонда, - ні былайша есептейміз:

Анықтама. Граф толық (ілмекпен) деп аталады, егер кез-келген екі төбесі сыбайлас болса, сонымен қатар әрбір төбеде ілмек болса. Мұндай графтардағы қабырғалар санын қайталанатын терулер формуласымен есептейміз, яғни 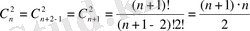қабырға.
Анықтама. графы графының ішкі графы деп аталады, егер төмендегі екі шарт орындалса:
1.
2. Егер қабырғасы және қабырғаларына инцидентті болса, онда қабырғасыда 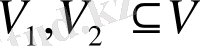қабырғаларына да инцидентті болады.

Маршруттар, жолдар, циклдер
Анықтама. 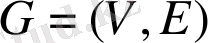графының 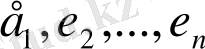қабырғаларының ақырлы тізбегі ұзындығы n-ге тең маршрут деп аталады, егер төбелеріне қабырғасы инцидентті болатын төбелер тізбегі бар болса. Егер 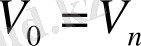болса, онда маршрут тұйық деп аталады.
Анықтама. Барлық қабырғалары әртүрлі болатын маршрутты жол деп атайды. Тұйық жол - цикл деп аталады. Қарапайым тұйық жол - қарапайым цикл деп атайды.
Байланыс
Анықтама. Егер графтағы кез-келген төбелердің жұбы кем дегенде бір тізбекпен байланысқан болса, онда мұндай графты байланысқан граф деп атайды. Қарама-қарсы жағдайда байланыспаған граф деп аталады.
7 - мысал.

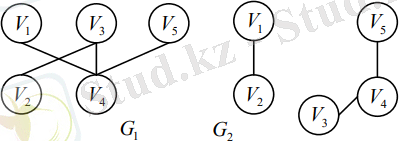
7 - сурет. Байланысқан және байланыспаған графтар. 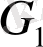- байланысқан граф, 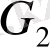- байланыспаған граф.

Ағаштар және ормандар.
Анықтама. Төбенің әрбір жұбын байланыстыратын тек бір ғана тізбегі бар, циклі жоқ графты ағаштар деп атайды. Сонымен ағаш деп циклі жоқ байланысқан графтарды атаймыз. Ағаштар T әрпімен белгіленеді.
k компоненттен тұратын, циклі жоқ графты орман деп атайды және F әрпімен белгіленеді.
T-ағылшын тіліндегі tree сөзінен бас әрібі, ағаш деген мағына білдіреді.
F- ағылшын тіліндегі forest сөзінің бас әрібі, орман деген мағына білдреді.
8 - мысал.

8 - сурет. Ағаштар.

және ағаш болып табылады. ағашында әрбір төбенің екі қабырғасы болғандық бинарлы ағаш деп аталады. және ағаштары екі ағаштан тұратын F орманын құрайды.

9 - сурет. Ағаш және граф. графта цикл болғандықтан ағаш бола алмайды.

Анықтама. Егер T ағашы G графының ішкі графы болса, онда T ағашына тиісті G графының қабырғасы T ағашының бұтағы деп аталады, ал T ағашына тиісті емес қабырғасы T ағашына қатысты хорда деп аталады.
10 - мысал. Бұтаққа және хордаға мысал келтірейік.

10 - сурет. Граф және ағаш.

Суретте T ағашы G графының ішкі графы болып тұр. T ағашы G графында қабырғаларын алып тастау арқылы пайда болған. Сондықтан G графының қабырғалары T ағашының бұтақтары болып саналады. қабырғалары T ағашына қатысты хорда болады.

Бағытталған графтар туралы түсінік

Көптеген жағдайларда графтың қабырғаларына бағыт беруге тура келеді. Бағытталған графтың бағытталмаған графтан айырмашылығы - бағытталмаған графтың қабырғаларының шекаралық нүктелері реттелмеген жұп құрайды. Бағытталған графтарда доғаның шекаралық нүктесі реттелген жұп құрайды.
Анықтама. Егер G=(V,E) графының қабырғалары реттеліп жұптасқан төбелер арқылы анықталатын болса, онда G=(V,E) графы бағытталған граф деп аталады. Мұндағы V- бос емес төбелер жиыны,
төбесімен сыбайлас дейміз, ал e доғасы төбесіне теріс инцидентті және төбесіне оң инцидентті деп аталады.
11 - мысал. Бағытталған графтарға мысалдар қарастырайық.

11 - сурет. Бағытталған графтар
графында төбесі төбесіне сыбайлас болады, ал e доғасы төбесіне теріс инцидентті, төбесіне оң инцидентті болады. графында төбесі төесімен сыбайлас, бірақ төбесі төбесімен сыбайлас емес, e доғасы төбесіне теріс инцидентті, төбесіне оң инцидентті болады.
графында доғасы төбесіне теріс инцидентті, төбесіне оң инцидентті болып саналады. доғасы төбесіне оң инцидентті, төбесіне теріс инцидентті болады және және төбелері бір-бірімен сыбайлас болады.
Анықтама. Егер доғасы төбесіне оң инцидентті және төбесіне теріс инцидентті болса, онда төбесі бастаптқы төбе деп аталады, ал төбесі ақырғы төбе деп аталады.

12 - сурет. Графтағы оң және теріс инциденттілік.

Суреттегі графта e доғасы төбесіне оң инцидентті, төбесіне теріс инцидентті болып тұр. e доғасы үшін төбесі бастапқы төбе, төбесі ақырғы төбе болады.
Анықтама. болғандағы доғасы ілмек деп аталады және деп белгіленеді. Бұл жағдайда V төбесі өз-өзіне сыбайлас болып табылады.

13 - сурет. Графтағы ілмек.

Суреттегі графта V төбесі өз-өзіне сыбайлас болады және доғасы ілмек болады.
Анықтама. Егер және доғаларының екеуініңде -бастапқы төбесі, - ақырғы төбесі болса, онда және доғалары қатаң параллель деп аталады.
Егер доғасының -бастапқы төбесі, - ақырғы төбесі болса және керісінше, доғасының - бастапқы төбесі, - ақырғы төбесі болса, онда онда және доғалары қатаң емес параллель деп аталады.

13 - сурет. Графтағы қатаң және қатаң емес параллель доғалар.
Суреттегі графта доғасының -бастапқы төбесі, - ақырғы төбесі болғандықтан, доғасының - бастапқы төбесі, - ақырғы төбесі болғандықтан және доғалары қатаң емес параллель болады. және доғалары қатаң параллель болады.
Егер доғасының бастапқы төбесімен доғасының ақырғы төбесі сәйкес келсе, онда және доғалары сыбайлас деп аталады.

14 - сурет. Графтағы доғалардың сыбайлас болуы.

1.2. Графтардың берілу тәсілдері, сандық сипаттамалары

Өлшенбеген, байланысқан, бағытталмаған G=(V,E); графын қарастырайық.
және арасындағы қарапайым тізбектің ең қысқа ұзындығы (қабырғалар саны). Егер және бір-бірімен байланыспаған болса, онда деп санаймыз. Мұндай қашықтық келесі метрикалық аксиомаларды қанағаттандырады:
1.
2.
3.
4.
Анықтама. төбесінің экцентриситеті деп шамасы аталады. Яғни төбесінен ең алшақ төбесіне дейінгі қашықтық төбесінің эксцентритеті деп аталады.
Анықтама. шамасы G=(V,E) графының диаметрі деп аталады. Яғни ең үлкен экцентритеттің өлшемі диаметр деп аталады.
Анықтама. Егер болса, яғни ең үлкен эксцентритеті бар төбе перифериялық төбе деп аталады.
Анықтама. шамасы G=(V,E) графының радиусы деп аталады. Яғни ең кіші экцентритеттің өлшемі граф радиусы болады.
Егер болса онда төбесі орталық төбе деп аталады.
Графты берудің бірнеше тәсілдері бар
1. Графикалық түрде.
2. Төбелер және қабырғалар жиыны түрінде.
3. Инциденттік матрица түрінде
4. Сыбайластық матрицасы түрінде.

Егер граф онша үлкен болмаса, графикалық түрде көрсетуге болады. Бағытталмаған графта қабырғалар сызық түрінде бейнеленеді, ал бағытталған графта көрсеткі (стрелка) арқылы бейнеленеді.
Графтарды төбелер және қабырғалар жиыны түрінде көрсетуге болады. Мысалы:
V={a,b,c,d,e},
E={(a,b),(a,c),(a,e),(b,c),(b,d)(c, e)(d,e)}.

Бағытталмаған графтың инциденттік матрицасы

n, төбеден тұратын және m, қабырғадан тұратын G=(V,E) графы болсын.
G=(V,E) графы үшін инциденттік матрицасы төмендегідей жазылады:

Мұндағы

Қасиеттері:
1.
Матрицаның әрбір бағанында екі бірлік болады. Егер ілмек болса, онда екі бірлік емес, екінің өзі болады. Матрицаның i-ші бағанының қосындысы екіге тең болады.

Матрицаның i-ші жолының қосындысы - ге тең болады.
2. Графты екі немесе одан көп байланыссыз компоненттерге бөлуге болатын кезде, бірінші компоненттің төбесі бірінші, екінші компоненттің төбесі екінші компоненттің төбесі екінші тағы сол сияқты нөмірленетін жағдайда, инциденттік матрица блок-диагональ түрінде болады.

15 - сурет. Байланыспаған граф.
Суреттегі граф үшін инциденттік матрицасын құрайық. қабырғасы және төбелерін қосатын болғандықтан бірінші бағандағы бірінші және екінші жолға 1-ді жазамыз. қабырғасы төбесінде ілмек болғандықтан бесінші бағандағы төртінші жолға 2-ні жазамыз. Осылайша толтырылғаннан кейін берілген графтың инциденттік матрицасы мынадай болады:

Бағытталмаған графтың сыбайластық матрицасы
n, төбеден тұратын G=(V,E) графы болсын.
G=(V,E) графы үшін сыайластық матрицасы төмендегідей жазылады:

Мұндағы - төбесіне бір уақытта инцидентті қабырғалар саны және
Қасиет. Бағытталмаған графтың сыайластық матрицасы әрқашанда бас диагональға қарағанда симметриялы матрица болады.

16 - сурет. Байланыспаған граф.
Cуреттегі графтың сыбайластық матрицасын құрайық. және төбелері бір қабырға арқылы байланысқандықтан бірінші жолдың бірінші бағанына және екінші жолдың бірінші бағанына 1- ді жазамыз. және төбелері екі қабырға арқылы байланысқандықтан төртінші жолдағы бесінші бағанға және бесінші жолдағы төртінші бағанға 2 - ні жазамыз. Егер графта ілмек бар болатын болса, онда ілмек сыбайласқтық матрицасында 1 цифрымен жазылады. Осылайша жазып болғаннан кейін сыбайластық матрицасы төмендегіше болады:

Сыбайластық матрицасы бас диагональға қарағанда симметриялы матрица болып тұр.

Бағытталған графтың инциденттік матрицасы
n, төбеден тұратын және m, қабырғадан тұратын G=(V,E) бағытталған графы болсын.
G=(V,E) бағытталған графының инциденттік матрицасы төмендегідей болады:

Мұндағы - дегеніміз:
0, егер доғасы төбесіне инцидентті болмаса;
1, егер доғасы төбесіне оң инцидентті болса;
-1, егер доғасы төбесіне теріс инцидентті болса;
2, доғасы төбесіне ілмек болса.

Бағытталған графтың сыбайластық матрицасы
n, төбеден тұратын G=(V,E) бағытталған графы болсын.
G=(V,E) бағытталған графтың сыбайластық матрицасы деп төмендегі матрица аталады:

Мұндағы - төбесінен төесіне бағытталған доғалар саны.

17 - сурет. Бастапқы граф.
Суреттегі бағытталған графтың инциденттік матрицасын құрамыз. доғасы төбесінен төбесіне қарай бағытталған, сондықтан бірінші бағанның біріні жолына 1-ді және бірінші бағанның екіні жолына -1-ді жазамыз. доғасы ілмек болғандықтан төртінші төртінші жолына 2-ні жазамыз. G=V,E бағытталған графтың инциденттік матрицасы төмендегіше болады:

Енді G=V,E бағытталған графтың сыбайластық матрицасын құрамыз. доғасы төбесінен төбесіне қарай бағытталғандықтан бірінші бағанның бірінші жолына 1-ді жазамыз. төбесінде ілмек болғандықан төртінші бағанның төртінші жолына 1-ді жазамыз және бұл бас диагональ бойындағы жалғыз бірлік болады.

Инциденттік және сыбайластық матрицаларының негізгі қасиеттері:
1. Бағытталмаған графтың инциденттік матрицасы симметриялы болады. Бағытталған графта бұл мүлде басқаша болады.
2. Бағытталмаған графтың сыбайластық матрицасындағы i-ші жолдың немесе i-ші бағанның элементтерінің қосындысы төбесінің дәрежесіне тең.
3. Бағытталған графтың сыбайластық матрицасындағы i-ші жолдың элементтерінің қосындысы төбесінен шығатын доғалардың санына тең.
4. Бағытталған графтың сыбайластық матрицасындағы i-ші бағанның элементтерінің қосындысы төбесіне келетін доғалардың санына тең.
5. Бағытталған графтың инциденттік матрицасындағы жолдардың қосындысы нөлдік жол болып табылады.

Сыбайластық тізімі

Сыбайластық тізімі әлсіз байланысқан графтың сыбайластық матрицасында көптеген нөлдерді сақтамау үшін қолданылады.
Анықтама. V төбелерінің сыбайластық тізімі деп жиынын айтады.

18 - сурет. Бастапқы граф.

Суреттегі графтың сыбайластық тізімін табайық. Сыбайластық тізімі төмендегіше болады:

1.3 Эйлерлік және гамильтондық графтар
Эйлерлік графтар
Графтар теориясының математиканың бөлімі ретінде дамуы Кеннигсерг көпірі туралы есеппен байланысты. Кеннингсберг (Калининград) қаласы Преголь өзенінің жағалауларында және екі аралында орналасқан. Қалада аралдарды өз-өзімен байланыстыратын және қаланың жағалауымен байланыстыратын жеті көпір болды. Үйден шығып, әрбір көпірден тек бір рет өтіп үйге қайтып келуг болама деген сұрақ туындады.

19 - сурет. Калининград көпірі.
Өзеннің құрғақ бөліктерін графтың төбесі ретінде A,B,C,D әріптерімен белгілейік. Ал мұндағы көпірлер қабырғалар болады.

20 - сурет. Калиниград көпірінің граф түріндегі көрінісі.

Сұрақ: Әрбір көпірден тек бір рет өтіп алғашқы нүктеге қайтып келуге болама?
Бұл есептің шешімі жоқ екенін Л. Эйлер дәлелдеді.
Анықтама. Егер цикл графтың барлық қабырғаларын қамтыса онла ол цикл эйлерлік цикл деп аталады. Эйлерлік циклі бар байланысқан граф эйлерлік граф деп аталады.

21 - сурет. Эйлерлік планарлы графтар.

Эйлерлік графтардың төбелерінің дәрежелері жұп екендігі туралы теорема.
Байланысқан граф эйлерлік граф деп аталады, тек сонда ғана барлық төбелерінің дәрежесі жұп болса.
Дәлелдеу.
1. Қажеттілік. G графы эйлерлік граф болсын. Бұл графтың байланысқан және барлық төбелерінің дәрежелері жұп екенін дәлеледейік. Бұл графтың эйлерлік циклі a) барлық қабырғаларды қамиды (демек, граф байланысқан) және б) төбеге бір қабырған келеді және бір қабырға шығады. Мұндай графтың әрбір төбесі жұп санды қабырғаларға инцидентті болады, демек әрбір төбенің дәрежесі жұп болады. Төбе арқылы өтетін қабырға осы төбенің дәрежесіне екі бірлік қосады.
2. Жеткіліктілік. Граф байланысқан және барлық төбелерінің дәрежесі жұп болсын. Осы графтың эйлерлік граф екенін дәлелдейік. Кез-келген төбесінен тізбесін құрамыз және әрбір жаңа қабырғалар арқылы тізбесін жалғастырамыз. Егер тізбесі төбесіне қайтып келсе, тізбесін құру аяқталады. Демек - цикл. Еер циклі графтың барлық қабырғаларын қамтитын болса, онда бұл эйлерлік цикл болады. Қарама - қарсы жағдайда G графынан циклін алып тастаймыз. Сонда графын аламыз. G графының және циклінің төбелерінің дәрежесі жұп болғандықтан графының да төбелерінің дәрежесі жұп болады. G графы байланысқан болғандықтан, және графтарының ең болмағанда бір ортақ төбесі болуы керек. Бұл төбені деп белгілейміз. G графында циклін құрған сияқты, графында цикл құрамыз.

22 - сурет. Эйлерлік графта төбелердің дәрежесі жұптығы туралы теоремаға иллюстрация.

циклі және төбелерінің арасын екі бөлікке бөледі. Оларды және деп белгілейміз және жаңа циклін аламыз. Егер - эйлерлік цикл болмаса, онда онда салуды жалғастырамыз. G графы ақырлы болғандықтан, құрылымды салу аяқталған кезед эйлерлік цикл аламыз.
Анықтама. Графтағы эйлерлік жол жеп аталады, егер кез-келген жол графтың қабырғаларынан тек бір рет өтсе.
Эйлерлі жол тақ дәрежелі төбеден басталып, басқа тақ дәрежелі төбеден аяқталады. Эйлерлік жол графта табылады сонда, тек сонда ғана, граф байланысқан және тақ дәрежелі төбелердің саны екіден артық болмағанда. Эйлерлік жол эйдерлік циклден қабырғаны жою арқылы алынады.

Гамильтондық графтар

Анықтама. Бағытталмаған байланысқан графтың барлық төбесін өзіне қамтитын қарапайым цикл гамильтондық цикл деп аталады.
Гамильтондық циклі бар граф гамильтондық граф деп аталады.
Гамильтондық сөзінің шығу тарихы математик Уильям Роуэн Гамильтон есімімен байланысты. 1959 жылы ол өзінің достарына Жер шарындағы саяхат атты ойынды ойнауды ұсынады. Гамильтон ойын үшін 20 төбеден тұратын граф салды. Әрбір төбе бір қаланы білдіреді. Ойынның мақсаты - әрбір қалада тек бір рет болып үйге қайтып келу. Ойынның мақсатынан көріп отырғанымыздай бұл барлық төбеден өтетін қарапайым циклді іздеуге алып келеді.

23 - сурет. Жер шарындағы саяхат графы.

Суретте гамильтондық циклі бар граф көрсетілген. Бұл графтың барлық төбесі барлық төбе қамтылатын рет бойынша нөмірленген.
Анықтама. Бағытталмаған графтағы графтың әрбір төбесі арқылы тек бір рет өтетін тізбені гамитольтондық тізбе деп атайды.

24 - сурет. Гамильтондық тізбе.

25 - сурет. Гамильтондық циклі және тізбесі жоқ балық графы.

1 - кесте. Эйлерлік және гамильтондық графтардың айырмашылығы

Эйлерлік цикл
Гамильтондық цикл
Эйлерлік цикл әрбір қабырғадан тек бір рет өтеді
Гамильтондық цикл әрбір төбеден тек бір рет өтеді
Эйлерлік цикл бір төбеден бірнеше рет өтуі мүмкін
Гамильтондық цикл кейбір қабырғалардан өтпеуі мүмкін

Гамильтондық циклдің бар болуының жеткілікті шарты.
Бағытталмаған графта гамильтондық циклдің бар болуының бірнеше жеткілікті шарттары бар.
1. Оре теоремасы. G=(V,E), графының кез - келген сыбайлас емес төбелер жұбы үшін теңсіздігі орындалса, онда G графы гамильтондық граф болып табылады.
2. Теорема. G=(V,E), графының кез - келген төбеcі үшін теңсіздігі орындалса, онда G графы гамильтондық граф болып табылады.
3. Кез-келген 4-байланысты планарлы граф гамильтондық граф болып табалады.

1.4 Графтардағы қысқа жолды табу. Дейкстр алгоритмі

Графтардағы қысқа жолды табу есебі графтар теориясының маңызды классикалық есебі болып табылады. Бұл есеп графтың кез қандайда бір төбесінен басқа кез - келген төбелерге дейінгі ең қысқа қашықты табудан тұрады.
Мұндай есептер классын шешу үшін қабырғаларына салмақтары жазылған өлшенген графтар (бағытталған графтар) қарастырылады. Қысқа жол табу есебін шешудің жалпы тәсілін американдық математик Ричард Беллман жасаған және мұндай есеп түрін динамикалық бағдарламалау деп атауды ұсынған. Қысқа жолды табу есебін келесідей тұжырымдауға болады: жолдар жиынының тиімділік критериі ретінде анықталған кейбір аддитивті функцияны минимумға немесе максимумға жеткізетін және берілген графтағы берілген екі төбені жалғастыратын жолдарды табу. Көбінесе бұл функция жолдың ұзындығы ретінде түсіндіріледі.
Графтардағы ең қысқа жолдың болуы үшін ұзындығы теріс болатын контурлардың жоқ болуы қажетті және жеткілікті.
Графтардағы ең қысқа жолды табудың әдістерінің бірі - Дейкстр алгоритмі болып саналады. Бұл алгоритм көбінесе белгі салу алгоритмі деп те аталады.
қабырғалары өлшенген, бағытталған граф берілсін. Жолдың басталу төбесін s (s төбесі) және жолдың аяқталу төбесін t (t төбесі) арқылы белгілейміз. s төбесінен төбесіне дейінгі қысқа жолдың бағалу мақсатында Дейкстр алгоритмінің жұмысы барысында бағытталған граф төбесіне саны (белгі) жазылады. Егер төбесіне қандай бір қадамнан кейін саны (белгі) жазылса, бұл G графта салмағы болтаын s төбесінен төбесіне дейін жол бар дегенді білдіреді. Белгілер екі жағдайда болуы мүмкін - уақытша немесе тұрақты. Уақытша белгінің тұрақты белгіге өтуі s төбесінен тиісті төбеге дейін қысқа жол табылғанын білдіреді. Дейкстр алгоритмінде барлық қабырғалардың салмағы оң болуы керек. Дейкстр алгоритмі екі этаптан тұрады. Бірінші кезеңде ең қысқа жол табылады, екінші кезеңде s төбесінен t төбесіне дейінгі табылған қысқа жол тұрғызылады.
Дейкстр алгоритмі
1 этап. Қысқа жол ұзындығының табылуы.
1 қадам. Төбелерге алғашқы белгіні салу
деп аламыз және бұл белгіні тұрақты деп есептейміз. қалған төбелер үшін деп алып, бұл белгіні уақытша деп есептейміз.
2 қадам. Белгілерді өзерту.
Ағымдағы төбені деп белгілейміз және бастапқыда деп аламыз. төбесі үшін келесі әрбір уақытша белгісі бар төбесінің белгісін келесі ереже бойынша өзгертеміз:

3 қадам. Уақытша белгінің тұрақты белгіге ауысуы.
Уақытша белгісі бар төбелердің ішінен белгісінің мәні ең кіші болатын төбесін таңдаймыз
уақытша белгі
Бұл белгіні тұрақты белгіге ауыстырамыз және деп аламыз.
4 қадам. 1 этаптың аяқталғандығын тексеру.
Егер онда s төбесінен t төбесіне дейінгі қысқа жолдың ұзындығы. Қарама - қарсы жағдайда 2 қадамға қайта ораламыз.
2 этап. Қысқа жолды құру
5 қадам. Біртіндеп қысқа жол қабырғаларын іздеу.
төбесінне тікелей алдыңғы және тұрақты белгісі бар төбелердің ішінде төбесін таңдаймыз және ол келесі шартты қанағаттандыруы керек:

доғасын ізделінді жолға қосамыз және деп есептейміз.
6 қадам. 2 этаптың аяқталғанын тексеру
Егер болса, қысқа жол табылған болып табылады - ол бесінші қадамда алынған және кері ретпен салынған доғалар тізбегін құрайды. Қарама - қарсы жағдайда 5 қадамға қайта ораламыз.
Мысал. Құрылыс компаниясының 1 қоймасы және 6 құрылыс алаңы бар. Бұл граф түрінде көрсетілген. 7-ші түйін (төбе) қойма және қалғандары құрылыс алаңдары. Қоймадан нөмірі бірінші құрылыс ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.