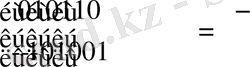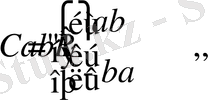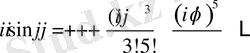Коши-Риман теңдеулерінің шешімдері және элементар голоморфтық функциялар


Мазмұны
Кіріспе . . . 3
1-тарау. Элементар голоморфтық функциялар
1. 1. Комплекс жазықтығының топологиясы . . . 10
1. 2. Дәрежелік қатарлардың комплекс жазықтығында жинақтылығы . . . 12
1. 3. Комплекс айнымалы экспоненциалдық функция . . . 13
1. 4. Тригонометриялық және гиперболалық функциялар . . . 16
1. 5. Комплекс айнымалы логарифмдік функция . . . 19
1. 6. Комплекс айнымалы жалпы дәрежелік функция . . . 20
1. 7. Кері тригонометриялық және кері гиперболалық функциялар . . . 22
2-тарау . Коши - Риман теңдеуінің шешімдерін зерттеу
2. 1. Голоморфты функциялар . . . 23
2. 2. Голоморфты функцияның әртүрлі интерпретациясы . . . 27
2. 3. Голоморфты функцияның гидродинамикалық интерпретациясы . . . 28
2. 4. Комплекс айнымалы функцияны интегралдау . . . 31
2. 5. Кошидың интегралдық теоремасы . . . 32
2. 6. Кошидің интегралдық формуласы . . . 38
2. 7. Голоморфты функцияның дәрежелік қатарға жіктелуі . . . 39
Қорытынды. . . . 42
Пайдаланылған әдебиеттер . . . 43
Кіріспе
Комплекс сандардың шығу тарихы
Жаңа теорияны меңгеру барысында, оның пайда болуының және қалыптасуының нақты тарихи жағдайын ескеру керек. Комплекс сандар, функциялар, комплекстік айнымалылардан және тіпті комплекстік анализдің алғашқы түрінен қазіргі осы шақтың түріне өте ұзақ эволюциялық жолдан өтіп келді. Комплекс сандардың тарихы шиеленіске толы. Алғашқы рет жорамал сандарды Дж. Кардано (1545) енгізген, бірақ оларды қолдануға жарамсыз деп есептеген. Кубтық теңдеуді шешу кезінде жорамал сандардың қажет екенін Р. Бомбелли (1572) көрсетті. 17-18 ғасырларда келесі түрдегі сан

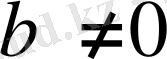 болғанда жорамал деп аталды. Алайда 17 ғасырдың өте атақты ғалымдарына жорамал сандардың қажеттілігі белгісіз және жұмбақ болды. И. Ньютон жорамал бөлікті сандар ұғымына қоспаған. 1707-1724 жылдары жаттығуларда жорамал бөліктің қолданылуын системалық түрде М. Муавр және Р. Котес бастады.
болғанда жорамал деп аталды. Алайда 17 ғасырдың өте атақты ғалымдарына жорамал сандардың қажеттілігі белгісіз және жұмбақ болды. И. Ньютон жорамал бөлікті сандар ұғымына қоспаған. 1707-1724 жылдары жаттығуларда жорамал бөліктің қолданылуын системалық түрде М. Муавр және Р. Котес бастады.
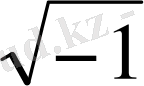 -ді
-ді
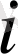 арқылы Л. Эйлер (1777) белгіледі. К. Гаусс (1799) комплекс сандардың жиыны алгебралық екенін дәлелдеді. Комплекс сандар ұғымын Л. Карно (1803) енгізді. Комплекс сандардың геометриялық интепретациясын К. Вессель (1799) және Ж. Арган (1803) енгізді 1851 жылы Б. Риман докторлық диссертациясын «Комплекс айнымалы функциялар теориясы» тақырыбында қорғады. Осы күнді ”
Комплекс айнымалы функциялар теориясы
” жаңа диссиплинаның туылу күні деп немесе КАФТ деп атайды. Совет үкіметі кезінде ең алғаш докторлық диссертацияны КАФТ бойынша А. И. Маркушевич қорғады, Семейдегі мектепті бітірген. Қазақстанда КАФТ бөлімдерін академик Н. К. Блиев пен М. Отелбаеваның жұмыстарынан көрініс табады. Ең алғаш КАФТ лекциясын қазақ тілінде Б. Тулегенов оқыды.
арқылы Л. Эйлер (1777) белгіледі. К. Гаусс (1799) комплекс сандардың жиыны алгебралық екенін дәлелдеді. Комплекс сандар ұғымын Л. Карно (1803) енгізді. Комплекс сандардың геометриялық интепретациясын К. Вессель (1799) және Ж. Арган (1803) енгізді 1851 жылы Б. Риман докторлық диссертациясын «Комплекс айнымалы функциялар теориясы» тақырыбында қорғады. Осы күнді ”
Комплекс айнымалы функциялар теориясы
” жаңа диссиплинаның туылу күні деп немесе КАФТ деп атайды. Совет үкіметі кезінде ең алғаш докторлық диссертацияны КАФТ бойынша А. И. Маркушевич қорғады, Семейдегі мектепті бітірген. Қазақстанда КАФТ бөлімдерін академик Н. К. Блиев пен М. Отелбаеваның жұмыстарынан көрініс табады. Ең алғаш КАФТ лекциясын қазақ тілінде Б. Тулегенов оқыды.
Қазіргі кезде математиканы комплекс сандарсыз елестету өте қиын. КАФТ математиканың ең әдемі бөліктерінің бірі. Бұл курстың мақсаты математиканың осы бөлігінің әдемілігін және қуаттылығын көрсету. Осының арқасында комплекс анализдің дамуы, яғни Риман кеңістігіндегі функциялар теориясы, комплекс айнымалының көптеген функциялар теориясын дамытты.
Нақты сандар жиынының кеңейтілуінің қажеттілігі
Натурал сандар үлкен емес сандарды санауға қажет.
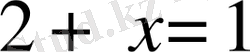 теңдеуінің натурал сандар жиынында шешімі жоқ, сондықтан натурал сандар жиынының дамуына қиындық соқты. Содан оның кеңейтілуі ұғымы пайда болды. Ол бүтін сандар жиыны деп аталды.
теңдеуінің натурал сандар жиынында шешімі жоқ, сондықтан натурал сандар жиынының дамуына қиындық соқты. Содан оның кеңейтілуі ұғымы пайда болды. Ол бүтін сандар жиыны деп аталды.
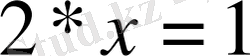 өрнегінің бүтін сандар жиынында жиынында шешімі жоқ. Осыдан бүтін сандар жиынының кеңейтілуіне келді. Оның кеңейтілуі рационал сандар жиыны болды.
өрнегінің бүтін сандар жиынында жиынында шешімі жоқ. Осыдан бүтін сандар жиынының кеңейтілуіне келді. Оның кеңейтілуі рационал сандар жиыны болды.
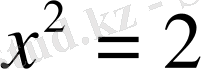 теңдеуінің рационал сандар жиынында шешімі жоқ, сондықтан рационал сандар жиынының кеңейтілуі ұғымы пайда болды. Оның кеңейтілуі нақты сандар жиыны болды
1
.
теңдеуінің рационал сандар жиынында шешімі жоқ, сондықтан рационал сандар жиынының кеңейтілуі ұғымы пайда болды. Оның кеңейтілуі нақты сандар жиыны болды
1
.
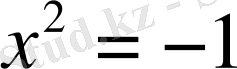 теңдеуінің нақты сандар жиынында шешімі жоқ, сондықтан нақты сандар жиынының кеңейтілуі мәселесі туындады
2
. Оның кеңейуі комплекс сандар болды. Бірақ бұдан комплекс сандар жиыны нақты сандар жиынының барлық қасиетіне ие бола бермейтінін айта кетейік. Нақты сандардың келесі қасиеттері бар.
теңдеуінің нақты сандар жиынында шешімі жоқ, сондықтан нақты сандар жиынының кеңейтілуі мәселесі туындады
2
. Оның кеңейуі комплекс сандар болды. Бірақ бұдан комплекс сандар жиыны нақты сандар жиынының барлық қасиетіне ие бола бермейтінін айта кетейік. Нақты сандардың келесі қасиеттері бар.
- Қосу мен көбейту амалдарына қарағанда коммутативті қасиеті
- Көбейту амалына қатысты қосу амалының дистрибутивтілігі
- Ассоциативтік
- Бірлік және нөлдік элементтің бар болуы
- Кері және теріс элементтің бар болуы
Сонымен қатар кез-келген екі нақты санның тізбек қатынасына бағынышты болғанына қарамастан, комплекс сандар жиыны реттелмеген.
Комплекс сандардың түрпаттары
Нақты сандардың түрпаттары әр түрлі екенін көрсетейік.
- Нақты сан ол ондық бөлшек.
- Нақты сан ол сан осіндегі нүкте.
- Нақты сан ол тесілген шеңбердегі нүкте.
Жоғарыда айтылған жиындар бір бірімен изоморфты, яғни әрбір жиындар жұбының арасында қосу мен көбейту амалдарын сақтайтын өзара бір мәнді сәйкестік бар. Математикада жеке объектілер емес, өзара изоморфты объектілердің кластары зерттеледі.
Мысалы: ехр(х) = -1
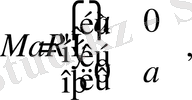
жиыны да нақты сандарға изоморфты яғни М жиынының элементтері нақты сан болып табылады.
Мақсаты:
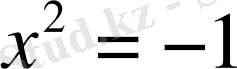 теңдеуі нақты сандар жиынында есептеу, яғни берілген теңдеуді ең болмағанда бір нақты сандардың ішінен іске асыру.
теңдеуі нақты сандар жиынында есептеу, яғни берілген теңдеуді ең болмағанда бір нақты сандардың ішінен іске асыру.
Теорема1.
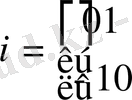 матрицасы
матрицасы
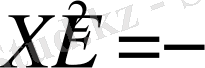 матрицалық теңдеуді қанағаттандырады.
матрицалық теңдеуді қанағаттандырады.
Дәлелдеуі матрицалық қатынастарын тікелей тексеруінде жатады.
Арнайы матрица жиынын енгізейік:
Теорема 2.
М жиыны мен
 матрица кеңейтілуі С ға тең
матрица кеңейтілуі С ға тең
Дәлелдеуі Егер
 , болса онда
, болса онда
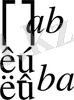 түріндегі матрица
түріндегі матрица
 жиынына тиісті болады. Егер
жиынына тиісті болады. Егер
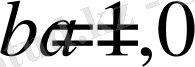 болса, онда
болса, онда
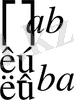 түріндегі матрица
і
матрицасымен беттеседі. Осылай
түріндегі матрица
і
матрицасымен беттеседі. Осылай
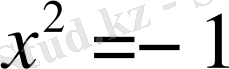 теңдеуі шешілетен нақты сандар жиынының кеңейтілуі С құрылады. Осындай кеңейтілулер көп.
теңдеуі шешілетен нақты сандар жиынының кеңейтілуі С құрылады. Осындай кеңейтілулер көп.
Комплекс сандардың алгебралық түрде жазылуы
Комплекс сан бұл арнайы
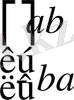 түріндегі матрица екені өткен дәрістен белгілі. Ыңғайымызға қарай бұл матрицаны екі бекітілгек матрицаның сызықтық комбинациясы ретінде алайық.
түріндегі матрица екені өткен дәрістен белгілі. Ыңғайымызға қарай бұл матрицаны екі бекітілгек матрицаның сызықтық комбинациясы ретінде алайық.
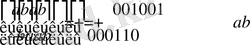
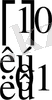 бірлік матрицасы М жиынына тиісті болғандықтан
бірлік матрицасы М жиынына тиісті болғандықтан
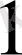 санына сәйекс келеді және оны жәй ғана бірлік деп атайтын боламыз. Екінші
санына сәйекс келеді және оны жәй ғана бірлік деп атайтын боламыз. Екінші
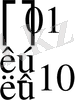 матрицасы 1 теоремада енгізілген i матрицасына сәйкес келеді және бұдан былай жорамал бірлік деп аталатын болады.
матрицасы 1 теоремада енгізілген i матрицасына сәйкес келеді және бұдан былай жорамал бірлік деп аталатын болады.
Тұжырым 1. Кез келген комплекс санды бір мен жорамал бірлік екеуінің сызықты комбинациясы түрінде жазуға болады.
Яғни:
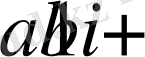
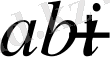 түрінде жазуға болады.
түрінде жазуға болады.
Сызықтық комбинациясының коэфициенттері нақты сандар екенін естен шығармау керек. Бірліктің алдындағы коэффициент комплекс санның нақты бөлігі деп, ал жорамал бірліктің алдындағы коэффициент жорамал бөлік деп аталады .
Міне осы комплекс санныңжазылуының алгебралық түрі.
Комплекс сандарды қосу мен азайту мүшелеп орындалады.
- Қосындының нақты бөлігі қосылғыштардың нақты бөліктерінің қосындысына тең
- Қосындының жорамал бөлігі қосылғыштардың жорамал бөліктерінің қосындысына тең
- ,
Келтірілген көбейту ережесін есте сақтау қиын. Сондықтан келесі жақшаны ашқан дұрыс:
ескерсек,
.
Комплекс сандардың тригонометриялық түрде жазылуы
Алдыңғы дәрісте келіскендей, комплекс сан-бұл
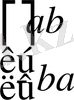 . түріндегі арнайы матрица.
. түріндегі арнайы матрица.
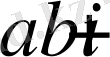 комплекс саны алгебралық түрде көрсетілген, яғни әрбір комплекс санның екі мінездемесі бар: нақты және жорамал бөліктер. Басқаша айтқанда комплекс сан
комплекс саны алгебралық түрде көрсетілген, яғни әрбір комплекс санның екі мінездемесі бар: нақты және жорамал бөліктер. Басқаша айтқанда комплекс сан
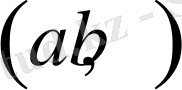 нақты сандар жұбымен бірмәнді анықталады. (a, b) жұбы жазықтықтағы вектрорды анықтайтын белгі.
нақты сандар жұбымен бірмәнді анықталады. (a, b) жұбы жазықтықтағы вектрорды анықтайтын белгі.
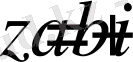 комплекс саны полярлық координаталар жүйесінде
комплекс саны полярлық координаталар жүйесінде
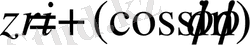 түрінде жазылады, мұндағы
түрінде жазылады, мұндағы
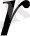
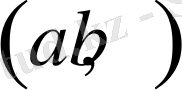 векторының ұзындығы,
векторының ұзындығы,

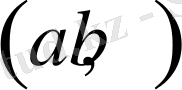 векторының бағытына сәйкес бұрыш. 1 суретте егежей тегежейлі көрсетілген.
векторының бағытына сәйкес бұрыш. 1 суретте егежей тегежейлі көрсетілген.
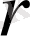 ді модулі деп, ал
ді модулі деп, ал
 бұрышын
бұрышын
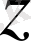 комплекс санның айғағы деп аталады, әрі сәйкес
комплекс санның айғағы деп аталады, әрі сәйкес
 және
және
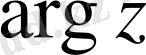 деп белгілейді. . Мысалы
деп белгілейді. . Мысалы
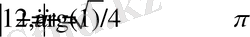 .
.
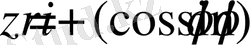 ұсынылуын комплекс санның тригонометрикалық түрі деп атайды.
ұсынылуын комплекс санның тригонометрикалық түрі деп атайды.
Комплекс сандардың көрсеткіштік түрде жазылуы
Комплекс санның әртүрлі ұсынуын еске түсірейік
- түрінде матрицаның дербес жағдайы,
- жорамал бірлігі мен нақты бірлігінің сызықты комбинациясы,
- полярлық координаталар системасында.
Бұл бөлімде комплекс сандар үшін жаңа түсінік енгіземіз.
Жаттығу 1. Жорамал бірліктің дәрежесі тек қана төрт мән қабылдайды.
Дәлелдеу
. Алдымен матрицалардың көбейтіндісімен келесі теңдіктерді тексереміз.
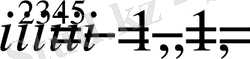 . Одан кейін
. Одан кейін
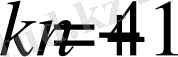 үшін теңдіктер қатарын жазамыз
үшін теңдіктер қатарын жазамыз
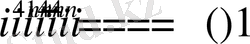 . Дәл осылай жолмен к ның кез келген мағынасында жазамыз
. Дәл осылай жолмен к ның кез келген мағынасында жазамыз
Жаттығу 2.
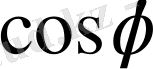 тригонометрикалық функциясы үшін Тейлор қатарының жазылуы сәйкес келеді, жорамал бірлігі үшін
тригонометрикалық функциясы үшін Тейлор қатарының жазылуы сәйкес келеді, жорамал бірлігі үшін
 сәйкес келеді.
сәйкес келеді.
Дәлелдеу.
Алдымен стандартты Тейлор қатарының ашылуын жазамыз:
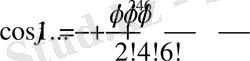 . . 5 жаттығу бойынша жорамал бірлігінің жұп дәрежелері +1 және -1 сандарын кезекпен қабылдап отырады. Бұдан біз 6 жаттығудағы тезисті аламыз. 6 жаттығудың дәлелдеуін келесіде дәлелдейді.
. . 5 жаттығу бойынша жорамал бірлігінің жұп дәрежелері +1 және -1 сандарын кезекпен қабылдап отырады. Бұдан біз 6 жаттығудағы тезисті аламыз. 6 жаттығудың дәлелдеуін келесіде дәлелдейді.
Жаттығу 3.
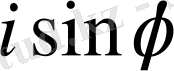 Тейлор қатарына жіктеледі.
Тейлор қатарына жіктеледі.
Мұнда таңбалардың кезектесуі болмайды.
Өткен жаттығулардың тривальдық салдары.
Теорема3.
Жорамал аргуменді бар экспонентал функцияны тригонометриялық функциялардың сызықты комбинациясы түрінде жазуға болады, яғни барлық нақты
 де
де
 теңдігі дұрыс.
теңдігі дұрыс.
Дәлелдеу . 3-жаттығудан келесі теңдік белгілі
жаттығудан
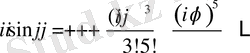 Екі теңдіктің оң жақтарын қосып, экспоненттің Тейлор қатарына жіктелуін аламыз. Үшінші теореманың салдары ретінде комплекс санның экспоненті
Екі теңдіктің оң жақтарын қосып, экспоненттің Тейлор қатарына жіктелуін аламыз. Үшінші теореманың салдары ретінде комплекс санның экспоненті
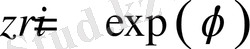 , көрінісін аламыз. Мұндағы
, көрінісін аламыз. Мұндағы
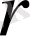 - комплекс санның модулі деп аталады, ал
- комплекс санның модулі деп аталады, ал
 комплекс санның аргументі деп аталады.
комплекс санның аргументі деп аталады.
Комплекс сандарға қолданылатын амалдардың герметриялық интерпретациясы
Сонымен комплекс сандар бірнеше түрде көрініс табады, матрицалық, алгебралық, көрсеткіштік және тригонометриялық. Матрицалық түрі комплекс сандардың бар екенін түсіндіретіні көрсетілді. Енді алгебралық түрдің комплекс сандардың қосындысының геометриялық түсіндірмесі арқылы ақиқат екенін көрсетейік . Экспонентті түр көбейту мен комплекс саннан алынған қандай да бір дәрежедеі түбірді тапқанда керек. Тригонометрикалық түрді қолданып Муавр формуласын жазған дұрыс.
Комплекс сандардың қосындысы векторлардағыдай үшбұрыш ережесі арқылы іске асады. Қосындыны алгебралық түрде жазған ыңғайлырақ:
Көбейтіндінің геометриялық интерпретациясы
Комплекс санның көбейтіндісін экспоненциалдық формуланы қолданып жазған дұрыс.
Комплекс сандардың аргументтерінің геометриялық қосындысының мағынасы: үлкен аргументті бұрыштың кіші аргументке тең бұрышқа санның сағат тіліне қарсы бағытқа бұрылуы. Суретте

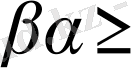 , болатындай
, болатындай
 бұрышқа бұрылған.
бұрышқа бұрылған.
Жаттығу 4. Бөлудің геометриялық интерпретациясын көрсет.
Натурал дәрежелі түбірлердің геометриялық бейнесі комплекс сандардан болады.
 , болғандықтан
, болғандықтан
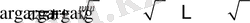 немесе
немесе
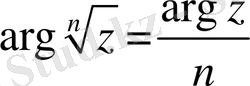 . Яғни түбірлерінің бірінің аргументтерін табу үшін
. Яғни түбірлерінің бірінің аргументтерін табу үшін
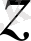 аргументін
аргументін
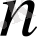 ге бөлу керек. Басқаша айтқанда
ге бөлу керек. Басқаша айтқанда
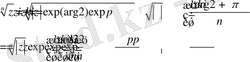
М ұндағы
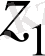 -бірінші түбір. Бұдан шығатын қорытынды, келесі түбірлер бірінші түбірден аргументтің мәнімен ғана ерекшкелінеді. Басқаша айтқанда, келесі түбірлерді бірінші түбірді
-бірінші түбір. Бұдан шығатын қорытынды, келесі түбірлер бірінші түбірден аргументтің мәнімен ғана ерекшкелінеді. Басқаша айтқанда, келесі түбірлерді бірінші түбірді
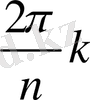 . Бұрышқа бұрғанда алынады. Мұндай бұрулар жазықтықта
. Бұрышқа бұрғанда алынады. Мұндай бұрулар жазықтықта
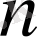 . ге тең болуы мүмкін. Сонымен, барлық түбірлер бір шеңбердің бойында жатады, және бұл шеңберді
. ге тең болуы мүмкін. Сонымен, барлық түбірлер бір шеңбердің бойында жатады, және бұл шеңберді
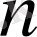 бөлікке бөледі. Келесі суретте 4 дәрежелі жорамал бірліктен алынған түбірлер көрсетілген. .
бөлікке бөледі. Келесі суретте 4 дәрежелі жорамал бірліктен алынған түбірлер көрсетілген. .
Комплекс санда берілген
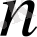 -дәрежелі алгоритм арқылы табуға болады.
-дәрежелі алгоритм арқылы табуға болады.
- санның аргументін ге бөлеміз және жазықтықта бұрышқа сәйкес аламыз.
- берілген санның модуліне тең түбірдің ұзындығын сәулеге өлшейміз.
Сол ұзындыққа сәйкес белгіленген нүкте арқылы және координат басы центрі болатын шеңбер саламыз. Шеңберді
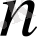 бөлікке бөлеміз, бөліну нүктесі сәуледегі белгіленген нүкте мен сәйкес келуі керек.
бөлікке бөлеміз, бөліну нүктесі сәуледегі белгіленген нүкте мен сәйкес келуі керек.
Дипломдық жұмыстың мақсаты: Коши - Риман теңдеулер жүйесінің шешімдерін, яғни голоморфты функцияларды зерттеу.
 1-тарау. Элементар голоморфтық функциялар
1-тарау. Элементар голоморфтық функциялар
1. 1 . Комплекс жазықтығының топологиясы
Әрбір комплекс санның модулі бар. Кереметтілігі, екі санның айырымының модулі келесі қасиеттерге ие болуы:
- Теріс еместігі, яғникез-келгенүшін;
- сонда және тек сонда ғанаболса;
- симметриялығы, яғникез-келгенүшін;
- үшбұрыш теңсіздігі, яғникез-келгенүшін.
Соңғы қасиет, екі санның айырымының модулі осы сандардың барлық мүмкін болатын ара-қашықтығында минимумға жететінін білдіреді. Басқаша айтқанда, экстремалды қатынасы орындалады.
Айырымның модулі
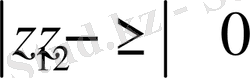 көрсетілген экстремалды қасиетке ие болғандықтан, оны осы сандар арасындағы қашықтығы деп атайды, ал минимумға жететін кесіндіні -геодезиялық сызық. Элементтер арасындағы қашықтықты енгізісімен, жинақтылық, шек, үзіліссіздік және т. б. түсініктерін енгізуге болады. Сонымен бірге, математикалық анализ курсында берілген анықтамалар сөзбе-сөз қайталанады. Бірақ мағынасы бойынша кейде нақты анализде болғаннан айырмашылығы болуы мүмкін.
көрсетілген экстремалды қасиетке ие болғандықтан, оны осы сандар арасындағы қашықтығы деп атайды, ал минимумға жететін кесіндіні -геодезиялық сызық. Элементтер арасындағы қашықтықты енгізісімен, жинақтылық, шек, үзіліссіздік және т. б. түсініктерін енгізуге болады. Сонымен бірге, математикалық анализ курсында берілген анықтамалар сөзбе-сөз қайталанады. Бірақ мағынасы бойынша кейде нақты анализде болғаннан айырмашылығы болуы мүмкін.
- жазықтығындағы ашық шар, мұндағы- оның центрі, ал- радиусы. нүктесінің маңайы.
- Жиынның ішкі нүктесі болады, егер нүкте өзінің қандай да бір маңайымен бірге жиынға тиісті болса.
- Ашық жиын тек ішкі нүктелерден тұрады. Кез-келген ашық жиын, центрлері жиынның нүктелерінде болатын қандай да бір ашық шарлардың бірігуі болып табылады.
- Тұйық жиын - бұл ашық жиынның толықтауышы. Кез-келген тұйық жиын, центрлері жиынның сыртында жататын ашық шарлардың толықтауыштарының қиылысуы болып табылады.
- Топология - бұл барлық ашық жиындардың жиыны. Анықтама бойынша бос жиынды ашық жиын деп санаймыз.
- Комплекссанын комплекс сандардыңтізбегінің шегі деп айтамыз, егер центрінүктесінде жататын әрбір ашық шар үшін бүкіл тізбек, мүмкін оның элементтерінің ақырлы санынан басқа, осы шарға тиісті болса. Онда тізбек жинақты дейді.
- Комплекссаны, шегі, ол функцияның анықталу облысының шектік нүктесі болады, егер центрінүктесінде жататын әрбір ашық шар үшін, мүмкін болатын-бейнелері, алдын-ала таңдап алынған центрі-да жататын ашық шарда тесілген маңайы бар болса.
- Нүктедегі функцияның шегі осы нүктедегі функцияның мәніне сәйкес келгенде, функция сәйкес нүктеде үзіліссіз болады.
Математикалық анализ курсынан белгілі анықтамаларды жалғастыруға болады. Математикалық анализ нәтижелерін комплекс анализге де көшіруге болатын бір диаграмманы көрсеткен дұрысырақ болады.
Диаграммада өзара-бірмәнді сәйкестік тек комплекс жазықтығы мен
 жиынының арасында ғана емес, сонымен қатар, комплекс мағыналы функциялар мен екі айнымалы бойынша нақты мәнді жұптар арасында бар екенін көреміз. Сондықтан комплекс айнымалы функцияның жинақтылығын, үзіліссіздігін зерттеу жұмысын, екі айнымалыдан алынған нақты функция жұбын зерттейтін эквивалентті есеппен алмастыруға болады. Мысалға,
жиынының арасында ғана емес, сонымен қатар, комплекс мағыналы функциялар мен екі айнымалы бойынша нақты мәнді жұптар арасында бар екенін көреміз. Сондықтан комплекс айнымалы функцияның жинақтылығын, үзіліссіздігін зерттеу жұмысын, екі айнымалыдан алынған нақты функция жұбын зерттейтін эквивалентті есеппен алмастыруға болады. Мысалға,
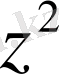 функциясы комплекс жазықтығында үзіліссіз, себебі
функциясы комплекс жазықтығында үзіліссіз, себебі
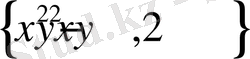 функциялар жұбы үзіліссіз.
функциялар жұбы үзіліссіз.
Қорытындысында университеттердің оқулықтарында жазылмайтын үзіліссіздік критериін берейін. Бірақ критерий экономикада, нақты айтқанда қолдану теориясында қолданылады, егер пайдалылық функциясының үзіліссіздігі дәлелденген жағдайда.
Теорема 4 . Функция анықталу облысында үзіліссіз, сонда және тек сонда ғана, егер мәндер жиынына қатысты әрбір тұйықтың түпбейнесі анықталу облысына қатысты тұйық болса.
1. 2 . Дәрежелік қатарлардың комплекс жазықтығында жинақтылығы
Толық баяндама үшін дәрежелік қатарлардың жинақтылығын нақтырақ зерттейік.
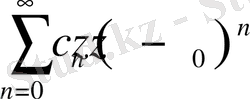 дәрежелік қатарын қарастырайық. Дәрежелік қатарлар нақты анализде керемет қасиеттер қатарына ие болғанын еске түсірейік:
дәрежелік қатарын қарастырайық. Дәрежелік қатарлар нақты анализде керемет қасиеттер қатарына ие болғанын еске түсірейік:
- Центрінүктесінде болатын симметриялы жинақтылық интервалы бар және бұл интервалдың сыртында жинақсыз;
- Формалды дифференциялдау жинақтылық интервалының радиусын кішіретпейді және үлкейтпейді;
- Жинақтылық интервалының ішінде дәрежелік қатар бірқалыпты жинақталады.
Көрсетілген қасиеттер комплекс жазықтығындағы дәрежелік қатарлар үшін де күшін сақтайды, егер жинақтылық интервалын жинақтылық дөңгелегімен алмастырсақ. Оның үстіне, математикалық анализ курсының дәрежелік қатарлар үшін дәлелдеулері де сақталады, егер абсолют шаманы комплекс санының модулі деп түсінсек.
Жаттығу 5.
Егер дәрежелік қатар
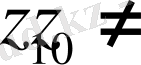 нүктесінде жинақталса, онда ол барлық
нүктесінде жинақталса, онда ол барлық
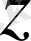 үшін бірқалыпты жинақталады, олар үшін келесі теңсіздік орындалады
үшін бірқалыпты жинақталады, олар үшін келесі теңсіздік орындалады
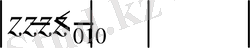 .
.
Дәлелдеу үшін қатарды эквивалентті түрде
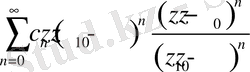 жазып, және
жазып, және
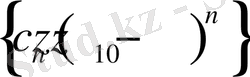 тізбегі шектелген,
тізбегі шектелген,
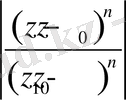 модулі бірден кіші екенін еске түсірген жеткілікті.
модулі бірден кіші екенін еске түсірген жеткілікті.
Бұдан салдар ретінде жинақтылық дөңгелегінің бар болуы шығады. Мұндағы жинақтылық радиусын Коши-Адамар формуласымен табуға болатынын ескерте кетейік. Кейінірек, жинақтылық радиусы үшін формула орынды екені дәлелденеді.
Тұжырым 2. Жинақтылық радиусы, центрден қатар қосындысының ең жақын жатқан ерекше нүктесіне дейінгі ара-қашықтығына тең. Басқаша айтқанда, жинақтылық дөңгелегінің шекарасында қатардың ерекше қосындысының болуы қажет.
Қатар қосындысы ерекше нүктеде шектелмеген немесе голоморфтылықтың бұзылуы басқа бір себептен болатынын еске салайық.
Ұқсас тұжырым нақты сандардан алынған дәрежелік қатарлар үшін орындалмауы мүмкін, егер жинақтылықты осьте қарастырсақ. Мысалға,
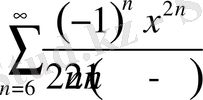 қатарының бірге тең жинақтылық радиусы бар, әрі қатар
қатарының бірге тең жинақтылық радиусы бар, әрі қатар
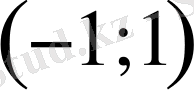 интервалының шекарасында жинақты.
интервалының шекарасында жинақты.
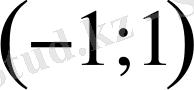 интервалдың сыртында қатардың жинақталуына не кедергі болғаны түсініксіз. Сол уақытта,
интервалдың сыртында қатардың жинақталуына не кедергі болғаны түсініксіз. Сол уақытта,
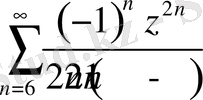 дәрежелік қатардың, ерекше нүкте ретінде жорамал бірлігі бар қосындысы бар. Бұтақтанудың арқасында көрсетілген нүктеде жинақтылық
дәрежелік қатардың, ерекше нүкте ретінде жорамал бірлігі бар қосындысы бар. Бұтақтанудың арқасында көрсетілген нүктеде жинақтылық
1. 3. Комплекс айнымалы экспоненциалдық функция
Экспоненциалдық функцияның анықталуы. Комплекс айнымалы экспоненциалдық функцияны e z (expzқылы да белгілейді) нақты аргументті экспоненциалдық функция е х сияқты мына шектік арақатынаспен
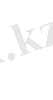
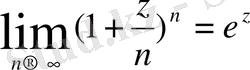 (1. 1)
(1. 1)
анықтауға болады.
 үшін осы шектің бар болғандығын дәлелдейік. Ол үшін
үшін осы шектің бар болғандығын дәлелдейік. Ол үшін
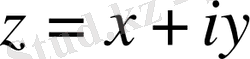 екенін еске алып, комплекс сандар тізбегі
екенін еске алып, комплекс сандар тізбегі
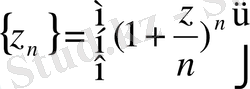 -нің шегі де е
z
комплекс саны болады деп ұйғарып, ол комплекс санды тригонометриялық формада былайша жазайық:
-нің шегі де е
z
комплекс саны болады деп ұйғарып, ол комплекс санды тригонометриялық формада былайша жазайық:
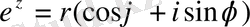 . Ендігі мақсатымыз осы r мен
. Ендігі мақсатымыз осы r мен
 -ді табу; олар мына шектерден
-ді табу; олар мына шектерден
 ,
,
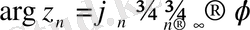 табылатыны белгілі. Сондықтан
табылатыны белгілі. Сондықтан
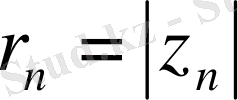 шегін табу үшін алдымен z
n
-нің өзін біраз түрлендіріп алайық:
шегін табу үшін алдымен z
n
-нің өзін біраз түрлендіріп алайық:
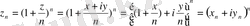 ,
,
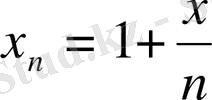 ,
,
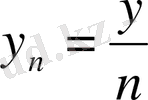 .
.
Сөйтіп, z n комплекс саны х n +iy n -нің натурал n дәрежесі ретінде қаралады. Сонда
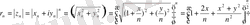 ;
;
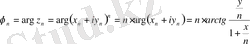 .
.
Мына теңдеулерден :
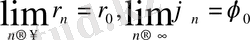
 шек тапсақ, онда r мен
шек тапсақ, онда r мен
 табылар еді:
табылар еді:
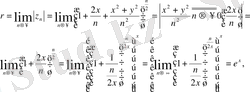
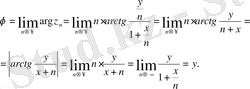
Демек, (1. 1) шегі бар, ол шек
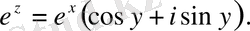 (1. 2)
(1. 2)
Міне комплекс аргументі экспоненциалдық функция expz осылай анықталады. Сөйтіп,
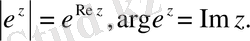
Бұл (1. 2) өрнегінен экспоненциалдық функция мен тригонометриялық функциялар өзара тығыз байланысты екені көрінеді және (1. 2) -нің оң жағы expz функциясының тригонометриялық формасы болып табылады.
Экспоненциалдық функцияның негізгі қасиеттері
1 0 . expz=e z бүкіл комплекс жазықтықта аналитикалық функция. Шынында да (1. 1) -дің нақты және жорамал бөліктері
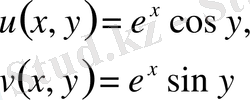
бүкіл комплекс жазықтықта Коши-Риманның шарттарын қанағаттандырады.
2
0
. Экспоненциалдық функцияның мәні бүкіл комплекс жазықтықта нольге айналмайды, яғни бүкіл комплекс жазықтықта expz функциясының нольдері жоқ. Шынында да, керісінше
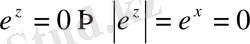 болуы мүмкін емес. Сөйтіп,
болуы мүмкін емес. Сөйтіп,
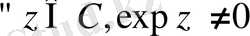 .
.
3
0
. expz үшін әдеттегі дифференциалдау ережесі сақталады. Шынында да,
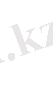
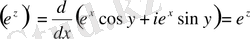 және
және
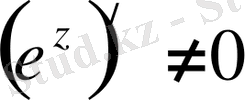 болғандықтан
болғандықтан
 бүкіл комплекс жазықтықта конформды.
бүкіл комплекс жазықтықта конформды.
4 0 . Экспоненциалдық функция үшін қосу теоремасы
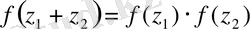
әділ, яғни
 (1. 3)
(1. 3)
Шынында да, егер z k =x k +iy k (k=1, 2) болса, онда нақты аргументті e x және тригонометриялық функциялардың қосу формулалары бойынша
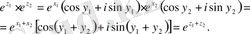
Сөйтіп,
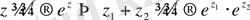 . Демек, (1. 3) бойынша
. Демек, (1. 3) бойынша
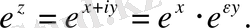
Осында
 болғанда және (1. 2) -ден Эйлер формулалары
болғанда және (1. 2) -ден Эйлер формулалары
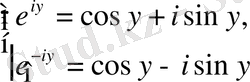 (1. 4)
(1. 4)
шығады. Сөйтіп,
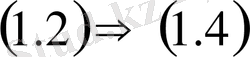 . Егер (1. 4) -те
. Егер (1. 4) -те
 болса, онда
болса, онда
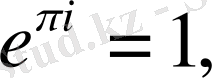 ал
ал
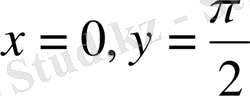 болса, немесе
болса, немесе
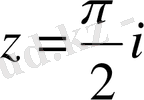 болса, онда
болса, онда
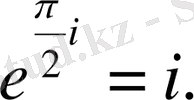 Әр түрлі сандардың арасындағы мұндай таңғаларлықтай байланысты есте қалдырған жөн.
Әр түрлі сандардың арасындағы мұндай таңғаларлықтай байланысты есте қалдырған жөн.
Осы (1. 4) Эйлер формулалары арқылы тригонометриялық формадағы комплекс сан
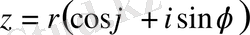 ықшамды түрде жазылады:
ықшамды түрде жазылады:
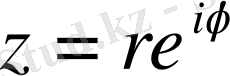 немесе
немесе
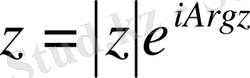 (1. 5)
(1. 5)
Бұл (1. 5) -тің оң жағын комплекс сан z-тің көрсеткіштік формасы деп атайды.
Сөйтіп, комплекс сан алгебралық, тригонометриялық және көрсеткіштік формада жазылады. Егер (1. 5) -ті n натурал санға дәрежелесе
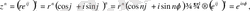
ал бұл кейінгі теңдік Муавр формуласының көрсеткіштік формасы.
5
0
. Экспоненциалдық функция e
z
периодты функция, оның периоды таза жорамал сан
 -ге тең.
-ге тең.
Шынында да, қосу теоремасы (1. 3) жәнеЭйлер формулалары (1. 4) бойынша
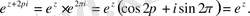 Сөйтіп,
Сөйтіп,
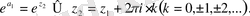 (1. 6)
(1. 6)
Бұдан экспоненциалдық функция бүкіл комплекс жазықтықты бірпарақты болмайтынын көреміз. Бұл expz функциясы
 облысында бірпарақты болуы үшін
облысында бірпарақты болуы үшін
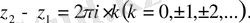 (1. 7)
(1. 7)
теңдігін қанағаттандыратын нүктелер ол облыстың нүктелері болмауы керек, өйткені бұл (1. 7) теңдікті қанағаттандыратын комплекс жазықтықтың
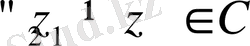 нүктелерінде expz мәндері (1. 6) бойынша өзара тең болады. Ендеше геаметриялық тұрыдан қарағанда ені
нүктелерінде expz мәндері (1. 6) бойынша өзара тең болады. Ендеше геаметриялық тұрыдан қарағанда ені
 -ге тең, ОХ осіне параллель мына D жолақтардың әрқайсысында
-ге тең, ОХ осіне параллель мына D жолақтардың әрқайсысында
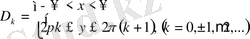 (1. 8)
(1. 8)
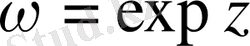 мәндері әр түрлі болады (2-сурет) .
мәндері әр түрлі болады (2-сурет) .
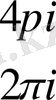
Сонымен, мұндай
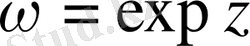 көппарақты функция қатарына жатады, ал ол (1. 8) жолақтардың әрқайсысындағана бірпарақты болады. Шынында да,
көппарақты функция қатарына жатады, ал ол (1. 8) жолақтардың әрқайсысындағана бірпарақты болады. Шынында да,
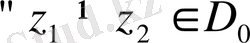 екі нүктесі
екі нүктесі
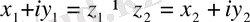 болса (2-сурет), онда
болса (2-сурет), онда
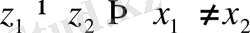 бірақ,
бірақ,
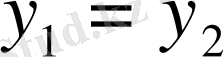 болса да
болса да
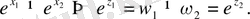
Ал егер
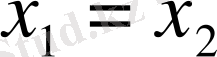 бірақ
бірақ
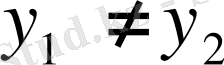 болса,
болса,
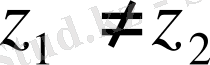 болады да, сонда
болады да, сонда
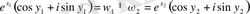 . Олай болса, бүкіл комплекс жазықтықта аналитикалық экспоненциалды функция expz (1. 8) жолақтардың әрқайсысында бірпарақты болады екен. Бұл ұйғару expz- тің конформды бейнесін қарағанда пайдаланылады.
. Олай болса, бүкіл комплекс жазықтықта аналитикалық экспоненциалды функция expz (1. 8) жолақтардың әрқайсысында бірпарақты болады екен. Бұл ұйғару expz- тің конформды бейнесін қарағанда пайдаланылады.
1. 4. Тригонометриялық және гиперболалық функциялар
Тригонометриялық және гиперболалық функциялардың анықталуы, арасындағы байланыс . Эйлер формулаларындағы (1. 4) у -тің орнына комплекс санның жалпы түрі z - ті қойсақ, сонда олардан комплекс айнымалылы тригонометриялық функциялар анықталады:
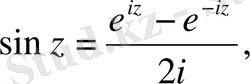
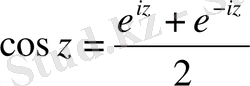 . (1. 9)
. (1. 9)
Гиперболалық синус, косинус нақты аргументті гиперболалық функциялар сияқты анықталады:
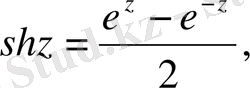
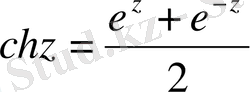 . (1. 10)
. (1. 10)
Осы (1. 9) және (1. 10) арқылы басқа тригонометриялық және гиперболалық функциялар анықталады да, олардың арасындағы байланыс та табылады:

Сөйтіп, комплекс айнымалылы тригонометриялық, гиперболалық және көрсеткіштік функцияларбір-бірімен өзара байланысты екен. Сондықтан да григонометриялық және гиперболалық функциялардың негізгі қасиеттері көрсеткіштік функцияның сәйкес қасиеттерінен шыға келеді.
Тригонометриялық және гиперболалық функциялардың негізгі қасиеттері. 1˚. Комплекс айнымалылы тригонометриялық синус және косинустың периодтары 2π-ге тең.
Тригонометриялық функциялардың бұл қасиеттері (3. 9) формулаларынан шығады. Шынында да,
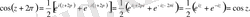
Басқа тригонометриялық функциялардың периодтары нақты аргументті функциялардың периодтарындай екені осы сияқты тексеріледі. Ал гиперболалық функциялардың периоды 2 π i -ге тең екені байқалады.
Тригонометриялық және гиперболалық функциялар үшін кәдуілгі дифференциалдау формуласы орындалады:
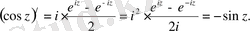
Осы сияқты (sin z ) ′=cos z , (sh z ) ′=ch z .
2˚.
 Equation. 3
- жұп функция, ал
Equation. 3
- жұп функция, ал
 Equation. 3
- тақ функция. Шынында да (1. 9) -дан
Equation. 3
- тақ функция. Шынында да (1. 9) -дан
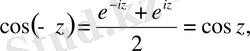
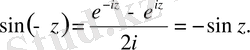
3˚. Комплекс айнымалылы синус пен косинус үшін нақты айнымалылы тригонометриялық функциялардың негізгі тепе-теңдіктері де орындалады:
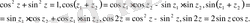
Шынында да,
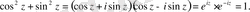 Ал
Ал
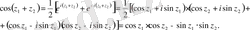
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz