Бос жиын

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 15 бет
Таңдаулыға:

М.Өтемісұлы атындағы Батыс Қазақстан университеті

Реферат

Тақырыбы: Жиын

Орындаған: Пимно у13тобы студенті
Жұмалиева Н.Е
Тексерген: Ерболат Б.Е

Орал 2022ж
Жоспар

I. Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 2
II. Негізгі бөлім
1.1 Жиындардың жазылуы мен оның берілу тәсілдері ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... .3
1.2 Бос жиындар ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...5
1.3 Тең жиындар ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...5
1.4 Ішкі жиындар ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..5
1.5 Жиындардың графикалық иллюстрациясы (сипаттамасы.) ... ... ... ... ... . ... ... ... ... ... ... ... 7
1.6 Универсал жиын ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..7
1.7 Жиындардың қиылысуы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .8
1.8 Жиындардың бірігуі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 8
1.9 Жиынның толықтауышы. Жиындардың айырмасы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 9
2. Кортеж ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .10
2.1 Реттелген жұптар ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..11
2.2 Жиындардың декарттық көбейтіндісі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..11
2.3 Жиындар элементтерінің арасындағы сәйкестіктер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..12
III. Қорытынды бөлім ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .13
Пайдаланылған әдебиеттер

Кіріспе

Математикада XIX ғасырдың екінші жартысында жиын ұғымы пайда болды. Жиын ұғымының математикаға енуі жиын теориясын қалыптастырды. Жиын теориясының негізін қалаушы неміс математигі Георг Кантор (1845-1918) болды.
Жиын ұғымы математикада негізгі (анықтауға болмайтын, бастапқы) ұғым болып саналады. Сондықтан оны тек мысылдармен ғана түсіндіруге болады. Мысалы, қайсыбір класс оқушыларының жиыны туралы, әлемдегі планеталар жиыны туралы айтуға болады. Жиын сөзі математикада жиынтық, класс, жинақ, коллекция деген сөздердің, яғни қайсыбір нәрселер жиынтығын сипаттайтын сөздердің орнына қолданылады, оның үстіне қарастырылып отырған жиынтықты бір ғана нәрсе болуы немесе бірде-бір нәрсе болмауы мүмкін. Жиын құратын кез-келген нәрселер (адамдар, үйлер, кітаптар, елдер, геометриялық фигуралар, сандар т. б.) оныңэлементтері деп аталады. Мысалы, 3 саны - бір таңбалы натурал сандар жиынының элементі. Жиын мен оның элементтерінің арасындағы элементті болады деген байланысты тиісті сөзінің көмегімен де білдіруге болады. Мысалы, 3 саны бір таңбалы натурал сандар жиынына тиісті деп айтуға болады. Соңғы сөйлемде символдың көмегімен қысқаша жазуға болады: 3ÏА. Бұл жазуда А әрпі арқылы бір таңбалы натурал сандар жиыны белгіленген (жиынды латын алфавитінің бас әріптерімен белгілейді), ал Î белгісі тиісті сөзін алмастырады. Жалпы аÎА жазуы а нәрсесі А жиынының элементті, немесе а нәрсесі А жиынына тиісті, немесе А жиынында а элементі бар деп оқылады. аÏА жазуын а нәрсесі А жиынына тиісті емес, немесе А жиынында а элементті жоқ, немесе а нәрсесі А жиынының элементі емес деп оқуға болады. Жиын элементтерінің саны шектеулі де, шектеусіз болуы мүмкін. Мысалы, қайсыбір педучилище оқушыларының жиының элементтерінің саны шектеулі, ал түзудегі нүктелер жиыны шектеусіз. Жиын ұғымы және онымен байланысты басқа да ұғымдар математиканы алғаш оқытудың негізі болады және онда кеңінен пайдаланылады. Кейбір оқулықтарда жиын термині кездеспейді, бірақ бұл ұғым айқындалмаған түрде пайдаланылады, ал бір қатар эксперимент кітаптарда жиын ұғымы символикасымен қоса айқын түрде пайдалалынылады. Сан, натурал сандарды қосу және көбейту амалдары және олардың қасиеттері, геометриялық фигура сияқты маңызды ұғымдардың қалыптасуы мектептегі математика курсында теориялық - жиындық негізде жүзеге асады.

2
Жиындардың жазылуы мен оның берілу тәсілдері

Егер әрбір нәрсе туралы оның жиынға тиісті немесе тиісті емес екендігін айта алатын болсақ, онда жиын берілген деп саналады.
Жиынды оның барлық элементтерін атау арқылы анықтап беруге болады. Егер де а, b, c, d - әр түрлі нәрселердің белгіленулері болса, онда осы нәрселердің жиынын А={ а, b, c, d } түрінде жазып, оны А жиыны а, b, c, d элементтерінен тұрады деп оқиды.Әр нәрсе жиынға тек бір рет қана енеді. Мысалы, 32 545 882 санының әр түрлі цифрларынан тұратын жиын {3, 2, 5, 4, 8}, ал есеп деген сөздегі әр түрлі әріптер жиыны {e, c, п} түрінде жазылады.
Жиынның берілуінің тағы бір тәсілі оны құрайтын нәрселердің ортақ қасиетін атау болып табылады. Мұндай қасиеттіcипаттамалық қасиет деп атайды. Мысалға, 7-ден кем натурал сандардың А жиынын қарастырайық. Бұл жерде А жиынының барлық элементтерінің ортақ қасиеті, атап айтқанда, олардың натурал және 7-ден кіші сан болуы аталып отыр.
Қарастырылып отырған А жиынының элементтерін атап шығу қиындыққа түспейді: А={1, 2, 3 ,4, 5, 6} Жиынның осылай берілу тәсілі математикада жиі қолданылады. Мысалға радиусы r, центрі О болатын шеңбердің центрі О және радиусы r болатын шеңбер деп жазықтықтың О нүктесінен r қашықтықта жататын нүктелер жиынын атайды деген анықтамасын еске түсірейік. О-дан r қашықтықта және бір жазықтықта жату - центрі О және радиусы r болатын шеңбердің барлық нүктелеріне тән қасиет және бұл қасиетке шеңберге тиісті емес бірде бір нүкте ие бола алмайды.Элементтердің сипаттамалық қасиеті көрсетілген жиынды былай жазуға болады: фигуралық жақшалар ішіне алдымен элементтерінің белгіленуін жазады. Содан кейін вертикаль сызықша қояды да сызықшадан соң осы жиын элементтеріне және тек соларға ғана тән қасиетті жазады. Мысалы, 7-ден кіші натурал сандар жиыны А былайша жазылады: А={xx- натурал сан, x7} Сонымен, қандай да бір жиын берілген болуы үшін не оның элементтерін атап шығу, не оның элементтеріне тән қасиетті көрсету керек. Екінші тәсіл біріншіге қарағанда жалпылау екенін айта кетеміз. Мәселе мынада: жиынның элементтерін атап шығу осы жиын шектеулі болғанда ғана мүмкін, ал жиын элементтерінің ортақ қасиетін жиын шектеулі болғанда ғана мү мкін, ал жиын элементтерінің ортақ қасиетін жиын шектеулі болса да, шектеусіз болса да көрсетуге болады.Бірақ кейбір кезде шектеусіз жиынды да бірінші тәсілді пайдаланып жазып көрсетуге болады. Мысалы, барлық натурал сандар жиынын N әрпі арқылы белгілеп мына түрде N=

3
{1, 2, 3, 4, ...} жазуға болады. Әрине жиынды тек көп нүктелер орнында не болатыны белгілі жағдайда ғана осы түрде жазуға болады. Барлық натурал сандардан және нольден тұратын жиынды N0 арқылы белгілеп, былай жазады: N0={1, 2, 3, 4, ...} Бұл жиынды оң бүтін сандар жиыны деп атайды. Барлық бүтін сандар жиынын Z әрпі арқылы белгілеу келісілген: Z={..., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5...}
Математиканы оқып-үйрену барысында шешуге тура келетін көптеген есептер элементтерінің ортақ қасиеті көрсетілген жиынды табумен байланысты болады. Бірнеше мысалдар келтірейік.
1-мысал. х(х-1)=0 теңдеуінің барлық түбірлерінің жиынын табу керек. Ізделінді А жиынының барлық элементтеріне тән ортақ қасиет -х(х-1)=0 теңдеуінің түбірі болу, яғни А жиынын А={x x(x-1)=0} түрінде жазуға болады. x(x-1)=0 - теңдеуін шешеміз. Екі х және х-1 сандарының көбейтіндісі, тек сол сандардың біреуі ноль болғанда ғана, нольге тең болатындықтан х1=0, х2=1 екендігін табамыз. Демек, А={0, 1}. 2-мысал. х5 теңсіздігінің шешімдерінің жиының табу керек. Ізделінді жиынды С деп белгілесек, оның барлық элементтеріне тән қасиет х5 теңсіздігінің шешімі болу, яғни С={x x5} болады. Бұл жерде C жиыны шектеусіз, оның элементтерін сандық түзу бойында көрсеткен ыңғайлы (1-сурет). 5 саны С жиынына тиісті болмағандықтан суретте оған сәйкес нүкте ақ күйінде қалдырылды.
Бастауыш кластардағы қазіргі математика оқулықтарында элементтері берілген белгілі қасиетке ие болатын жиындарды табу қажет болатын көптеген есептер бар. Мысалы, ²7-ге бөлгенде қалдықтары 1 болатын үш сан жазыңыздар², ²65- тен үлкен 75-тен кіші сандарды жазып шығыңыздар² деген сияқты есептер. Осыларға ұқсас есептерді бастауыш класс оқушылары қазақ тілі сабақтарында ²Қазақ алфавитіндегі барлық дауысты дыбыстарды атап шығыңыздар²; ²Берілген сөйлемдегі барлық зат есімдерді сызыңыздар²; ²Жаттығудағы барлық сын есімдерді көшіріңіздер² т. с. с. тапсырмаларды орындағанда да шешеді.

4
Бос жиын
Әр түрлі жиындардың арасында бірде бір элементі жоқ жиынды да кездестіруге болады. Мысалы, сіздің топтағы тенниспен айналысатын оқушылардың тізімін немесе, қысқаша айтқанда, сіздің топтағы теннисші - оқушылардың Т жиының құру керек дейік. Бірақ топта ондай оқушы жоқ болып шықты. Ендеше Т жиынында бірде бір элемент жоқ. Бірде бір элемент жоқ жиынды бос жиын деп атайды және оны Æ белгісімен белгілейді. Бос жиынмен теңдеулерді шешуде де кездестіруге болады. Мысалы, 3х-7=3(х+5) теңдеуінің түбірлерінің жиынын іздестіру керек болсын. Берілген теңдеу қажетті түрлендірулер арқылы 0xх=22 теңдігіне келтіріледі. Ал бұл теңдік хтің ешқандай мәнінде де тура емес. Бұл жағдайда берілген теңдеудің түбірі жоқ немесе басқаша айтқанда, берілген теңдеудің түбірлерінің жиыны бос жиын дейді.

Тең жиындар
Егер А және В екі жиын бірдей элементтерден тұратын болса, онда оларды тең жиындар деп атайды және А=В түрінде жазады. Мысалы, А={3, 5, 7, 9} және В={7, 3, 9, 5} жиындары өзара тең, өйткені бірдей элементтерден тұрады. Элементтерінің орындарын ауыстарғаннан жиын өзгермейді. Жиындардың тең болу ұғымы мына жағдаймен байланысты: бір ғана жиын мүлдем әр түрлі сипаттамалық қасиеттер көмегімен берілуі мүмкін. Мысалы А={1, 2, 3, 4, 5} жиынын және 5 сандарының аралығындағы натурал сандар жиыны немесе х6 теңсіздігінің натурал шешімдерінің жиыны деп те қарастыруға болады.

Ішкі жиындар
Айталық, А - сіздің мектептегі барлық оқушылар жиыны, ал В - сіздің кластағы оқушылар жиыны болсын. Әрине, В жиыны А жиынынның бір бөлігі, немесе, басқаша айтқанда, В жиыны А жиынына кіреді. Мұндай жағдайда В жиынын А жиынының ішкі жиыны деп атайды. Дәлірек айтсақ: В жиынының әрбір элементі А жиынына тиісті болғанда және тек сонда ғана, В жиыны А жиынының ішкі жиыны деп аталады, оны ВÌА (немесе АÉВ) түрінде жазып, ²В жиыны А жиынының ішкі жиыны² деп оқиды. Ì белгісі жиындар арасындағы ²ішкі жиыны болады² деген мағынадағы байланыстықты көрсетеді. Әрбір А жиыны өзінің ішкі жиыны болып табылады деп есептейді: АÌА. Сондайақ бос жиын Æ кез келген А жиының ішкі жиыны болады деп есептеледі: ÆÌА. А жиынының бос емес В ішкі жиыны А жиынымен дәлме-дәл келмейтін болса, онда оны меншікті ішкі жиын
5
деп атайды. А жиынының А және Æішкі жиындарын оның меншікті емес ішкі жиындары деп атайды. Мысалы, А={2, 4, 8} жиынының алты меншікті ішкі жиыны бар. {2}, {4}, {8}, {2, 4}, {2, 8}, {4, 8}; екі меншікті емес ішкі жиыны бар: {2, 4, 8} және Æ. Егер де АÌВ, ал ВÌС болса, онда АÌС екендігіне көз жеткізу қиын емес. Шынында да, А жиынының әрбір элементі В жиынына, ал сонымен қатар В жиынының әрбір элементі С жиынына тиісті. Ұғымдар немесе нәрселер жиынтықтарының әр түрлі бөліктерін қарастырғанда біз әрдайым ішкі жиын ұғымын пайдаланым отырамыз. Қазақ тілінде сөйлемдегі барлық сөздер жиынының әр түрлі ішкі жиындарын - сын есімдері, зат есімдері, етістіктерді, т. с. с. қарастырамыз. География және тарих сабақтарында барлық елдер, барлық қалалар т. с. с. жиындарының әр түрлі ішкі жиындарын оқимыз. Осы сияқты күнделікті өмірде де ішкі жиын ұғымымен пайдаланамыз. Мысалы, қайсыбір елді мекендегі бір көше бойындағы үйлер сол елді мекендегі барлық үйлер жиынының ішкі жиыны болады; сіздің пәтердің тұрғындары сіздің үйдің барлық түрғындары жиынының ішкі жиыны, бір бөлмедегі орындықтар жиыны - сіздің пәтеріңіздегі барлық орындықтар жиынының ішкі жиыны болып табылады т. с. с.
Ішкі жиын ұғымы математикада кеңінен пайданылады. 1-ден 10-ға дейінгі сандар жиынын натурал сандар жиынының ішкі жиыны, ал натурал сандар жиынының өзін барлық бүтін сандар жиынының ішкі жиыны деп қарауға болады. Ромбылар, квадраттар, тік төртбұрыштар жиындары параллелограмдар жиынының әр түрлі ішкі жиындары болып табылады. ²Берілген сөйлемдегі барлық зат есімдерді сызыңдар²; ²Әр түрлі ағаштардың арасынан мәңгі көгеріп тұратындарын атаңыздар², ²1-ден 10-ға дейінгі сандардың 2-ге бөлінетіндерін көрсетіңіздер²; ²Берілген сандардың арасынан үш таңбалы сандарды көрсетіңіздер²; ²Әр түрлі фигуралардың арасынан үшбұрыштарын табыңыздар²деген сияқты тапсырмаларды орындату арқылы қазақ тілі сабағында да, табиғаттану сабағында да, математика сабағында да төменгі класс оқушыларын жиынның бөліктерін ажырата білуге үйретеміз.

6
Жиындардың графикалық иллюстрациясы (сипаттамасы.) Эйлер-Венн диаграммалары
Кез келген жиынды графикалық түрде кескіндеуге болады. Ол үшін тұйық контур сызамыз да, жиынның элементтері осы контурдың ішіндегі нүктелермен кескінделген деп түсінеміз. Суретте нүктелерді жекелеп көрсету міндетті емес. Мысалы, 9-суретте біз А және В жиындарының элементтерін көрмесек те, тіпті олардың қандай жиындар екенін білмесек те, бұл сурет В жиыны А жиынының құрамына енетінін, яғни ВÌА екенін айтып тұр. Мұндағы А қайсыбір мектеп оқушыларының жиыны, ал В - осы мектептің екінші кластары оқушыларының жиыны, ал В 5-ке бөлінетін барлық натурал сандар жиыны болуы мүмкін.

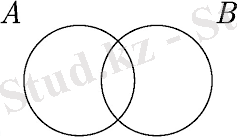
Жиындарды осылай кескіндеу тәсілі Эйлер дөңгелектері немесе Венн диаграммалары деп аталады. Осындай кескіндеулерді біз Эйлер-Венн диаграммалары деп атайтын боламыз.

Универсал жиын

А-қайсыбір мектептегі ұл балалар жиыны, В-осы мектептегі қыз балалар жиыны, ал С-осы мектептің спортсмендерінің жиыны болсын. Осы аталған жиындардың барлығын мектептің барлық оқушыларының жиынының ішкі жиындары деп қарастыруға болады. Барлық жиындары бір ғана I жиынының ішкі жиындары ретінде қарастыратын жағдай аз кездеспейді. Осындай I жиынын универсал жиын деп атайды. Ендеше, егер I - мектептің барлық оқушыларының жиыны болса, онда АÌI, ВÌI, СÌI болады. Универсал I жиынын тік төртбұрыш түрінде, ал оның ішкі жиындарын - осы тік төртбұрыштың ішіндегі дөңгелектер түрінде кескіндеуге келісейік. Онда біздің қарастырып отырған I, А, В, С жиындарын графикалық түрде мынадай (10- сурет) етіп кескіндеуге болады.
7
Жиындарға қолданылатын амалдар. Жиындардың қиылысуы
Екі жиынның элементтерінен жаңа жиындар құруға болады. А={0, 2, 4, 6} және В={-2, -1, 0, 1, 2} екі жиын берілген болсын. Элементтері берілген ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.