Кеңістіктегі түзулер мен жазықтықтардың теңдеулері және өзара қатынастары


РЕФЕРАТ
тақырыбы: Кеңістіктегі түзулер және жазықтықтар
Орындаған: Сатаева С
Тексерген: Ажымбаев Д
2022 жыл
Мазмұны
КІРІСПЕ
Геометрия (көне грекше: γεωμετρία; көне грекше: γῆ - жер и көне грекше: μετρέω - «өлшеу») - математиканың кеңістіктік пішіндер (формалар) мен қатынастарды, сондай-ақ, оларға ұқсас басқа да пішіндер мен қатынастарды зерттейтін саласы. Ғылым ретінде Ежелгі Грекияда математиканың бір бөлігі болып қалыптасқан, оның алғашқы аксиомалары Эвклидтың «Бастама» кітабында сипатталған.
Геометрия табиғатты зерттеуде, техниканы дамытуда қуатты құрал болып табылады. Ол математикалық анализге, механикаға, физикаға, астрономияға, геодезияға, картографияға, кристаллографияға, тағыда басқа ғылымдарға елеулі ықпал етеді.
Конустың қималары: шар, эллипс, парабола, гипербола
Фигуралар - кеңістіктік пішіндер болып есептеледі. Геометрия тұрғысынан сызық - “сым” емес, шар - “домалақ дене” емес, олардың барлығы да - кеңістіктік пішіндер. Ал кеңістіктік қатынастар - фигуралардың мөлшері мен орналасуын анықтайды. Мысалы, центрлері ортақ, радиустары 3 см және 5 см шеңберлер қиылыспайды, “біріншісі екіншісінің ішінде жатады” дегенде - шеңберлердің мөлшері мен орналасуы жөнінде айтылып тұр. Мұнда бірінші шеңбер - кішісі, екіншісі - үлкені, біріншісі екіншісінің ішінде орналасқан. Осыған орай кеңістіктік қатынастар “үлкен”, “кіші”, “ішінде”, “сыртында” сөздері арқылы анықталған. “Тең”, “параллель”, тағыда басқа сөздер де кеңістіктік қатынастарды сипаттайды. [1]
Дененің шекарасы - бет. Ол денені қаптап, қоршап, шектеп, кеңістіктен бөліп тұрады. Бет шектеусіз жұқа болып есептеледі. Жіңішке жіп, бір тал қыл, сәуле, сым, тағыда басқа негізінде шектеусіз жіңішке сызық ұғымы шыққан. Геометриялық денелерді ойша топшылап, шектеусіз кішірейте беруге болады. Осыдан нүкте ұғымы шығады. Нүкте дененің әбден кішірейіп, тоқтаған шектік жағдайы деп есептеледі. Геометрия тұрғысынан алғанда нүктені одан әрі кішірейтуге болмайды. Геометриялық денелердің, беттердің, сызықтардың және нүктелердің кез келген жиыны фигура деп аталады. Айтылып отырған негізгі ұғымдар - нүкте, сызық, бет, дене дүниедегі заттардан (яғни, материядан) алынған. Бірақ материяның физикалық қасиеттерінен абстракцияланған. Мысалы, призма жөніндегі теоремаларды ағаштан, тастан, металдан жасалған призмалардың бәріне де және әрдайым қолдана беруге болады. Геометрия алғашқы кезде фигуралардың мөлшерлерін, өзара орналасу тәртібін, бір түрден екінші түрге көшу жолдарын зерттейтін ғылым болды. Онда фигуралардың түрлендірілуі берілген фигура мен кейін пайда болған фигураның арасындағы белгілі бір қатынастар ретінде түсіндірілді. Мұндай түсінік осы күнгі геометрияда да бар. Алайда қазіргі геометрия байырғы түсініктер шебінен ұзап шығып кетті. Соңғы ғасырларда геометрияның үйреншікті ұғымдары мен қағидаларын талдау, жалпылау, жартылай өзгерту және одан әрі абстракциялау нәтижесінде математиканың бірталай жемісті теориялары шықты. Геометрияның жаңа салаларының көпшілігі ертеде қалыптасқан дәстүрлі салаларына мүлдем ұқсамайды. Мысалы, Георг Фридрих Бернхард Риман кеңістігіндегі “ара қашықтық”, Гильберт кеңістігіндегі “призма” ұғымдарын, жалпы түрде алғанда, ешқандай сурет, модель бойынша сипаттауға болмайды. Оларды дүниеде кездесетін нақты нәрселердің пішіндері мен қатынастары арқылы түсіндіру өте қиын. Сөйтсе де, Геометрияның байырғы салалары жаңа салаларының қарапайым дербес көріністері болып табылады. Сөз болып отырған жаңа теориялардың қайшылықсыздығы мұқият дәлелденген және олар күмәнсіз. Соңғы салалар да, тарихи жағынан геометрия шаңырағының астында туғандықтан және олардың заңдары бұрынғы геометрияның заңдарына сырттай ұқсас болғандықтан, геометрияға жатқызылады. Сөйтіп, геометрияның өрісі мүлдем кеңейіп кетті. Оның жоғарыда келтірілген анықтамасына “сондай-ақ, оларға ұқсас басқа да пішіндер мен қатынастарды зерттейтін” деген сөздер сондықтан қосылған. Осылай кең мағынада түсінген жағдайда ғана геометрия математиканың көптеген саласымен астасып жатады.
- Кеңістіктегі түзудің теңдеулеріТүзудің векторлық теңдеуі
Түзудің кез-келген
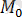 нүктесі және осы түзуге параллель
нүктесі және осы түзуге параллель
 векторымен анықталады.
векторымен анықталады.
 векторы түзудің бағыттауыш векторы деп аталады.
векторы түзудің бағыттауыш векторы деп аталады.
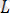 түзуі өзінің
түзуі өзінің
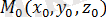 нүктесімен және
нүктесімен және
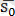 бағыттауыш векторымен берілсін. Түзудің бойынан кез-келген
бағыттауыш векторымен берілсін. Түзудің бойынан кез-келген
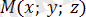 нүктесін белгілеп алайық.
нүктесін белгілеп алайық.
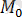 және
және
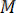 нүктелерінің радиус векторларын
нүктелерінің радиус векторларын
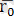 және
және
 арқылы белгілейік.
арқылы белгілейік.
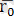 ,
,
 ,
,
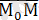 үш векторы
үш векторы
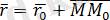
қатынасымен байланысты. L түзуінің бойында жатқан
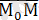 векторы
векторы
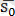 бағыттауыш векторына параллель, сондықтан
бағыттауыш векторына параллель, сондықтан
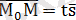 , мұндағы t-параметр деп аталатын скалярлық көбейткіш, ол түзудің М нүктесінен тәуелді әр түрлі мәндер қабылдайды. (1. 1) формуласын
, мұндағы t-параметр деп аталатын скалярлық көбейткіш, ол түзудің М нүктесінен тәуелді әр түрлі мәндер қабылдайды. (1. 1) формуласын
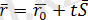
түрінде жазуға болады. Бұл шыққан теңдеуді түзудің векторлық теңдеуі деп аталады.
1. 2. Түзудің параметрлік теңдеуі
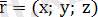 ,
,
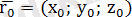 ,
,
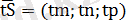 ескере отырып (1. 2) теңдеуін
ескере отырып (1. 2) теңдеуін
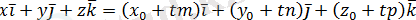
түрінде жазуға болады. Бұдан
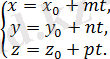
теңдігі шығады. Бұл теңдеуді түзудің параметрлік теңдеуі деп атайды.
1. 3. Түзудің канондық теңдеуі
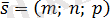 векторы L түзуінің бағытауыш векторы, ал M
0
(x
0
; y
0
; z
0
) нүктесі осы түзуде жататын нүктесі. L түзуінің бойындағы M(x; y; z) нүктесін M
0
нүктесімен қосып,
векторы L түзуінің бағытауыш векторы, ал M
0
(x
0
; y
0
; z
0
) нүктесі осы түзуде жататын нүктесі. L түзуінің бойындағы M(x; y; z) нүктесін M
0
нүктесімен қосып,
 векторына параллель
векторына параллель
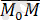 векторын жүргіземіз. Сондықтан,
векторын жүргіземіз. Сондықтан,
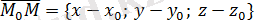 және пропорционал болады:
және пропорционал болады:
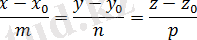
(1. 4) теңдеуі түзудің канондық теңдеуі деп аталады.
1. 4. Екі нүкте арқылы өтетін кеңістіктегі түзудің теңдеуі
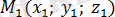 және
және
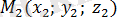 нүктелері арқылы өтетін L түзуі берілсін. Бағыттауыш
нүктелері арқылы өтетін L түзуі берілсін. Бағыттауыш
 векторы ретінде
векторы ретінде
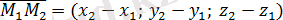 векторын алуға болады, яғни
векторын алуға болады, яғни
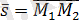 . Түзу M
1
(x
1
; y
1
; z
1
) нүктесі арқылы өтетін болғандықтан, (1. 4) теңдеуі бойынша, L түзуінің теңдеуі келесі түрде болады
. Түзу M
1
(x
1
; y
1
; z
1
) нүктесі арқылы өтетін болғандықтан, (1. 4) теңдеуі бойынша, L түзуінің теңдеуі келесі түрде болады
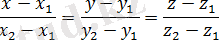
(1. 6) теңдеуі берілген екі нүкте арқылы өтетін түзудің теңдеуі деп аталады.
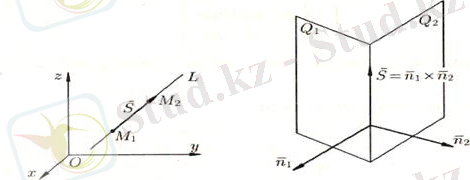
1. 5. Түзудің жалпы теңдеуі
Кеңістіктегі түзудің теңдеуі параллель емес екі жазықтық қиылсықанда пайда болған сызық арқылы беріледі
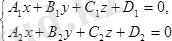
теңдеулер жүйесін қарастырайық. Бұл жүйенің әрбір теңдеуі жазықтықты анықтайды. Егер жазықтықтар параллель емес болса, онда (1. 7) жүйесі, координаталары осы жүйенің әрбір теңдеуін қанағаттандыратын, кеңістіктегі геометриялық орны болатын L түзуін анықтайды. (1. 7) жалпы теңдеуінен (1. 4) канондық теңдеу түріне келтіруге болады. (1. 7) жүйесіндегі теңдеулеріндегі координаталардың кез-келген біреуін нөлге теңестіріп, L түзуінің M
0
нүктесінің координаталарын табамыз. L түзуі
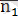 және
және
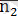 векторларына перпендикуляр болғандықтан, L түзуінің
векторларына перпендикуляр болғандықтан, L түзуінің
 бағыттауыш векторы ретінде
бағыттауыш векторы ретінде
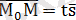 векторлық көбейтіндісін алуға болады:
векторлық көбейтіндісін алуға болады:
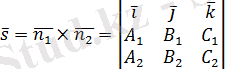
- Кеңістіктегі жазықтық теңдеуі
Қарапайым беттердің бір түрі жазықтық. O xyz кеңістіктегі жазықтықты әр түрлі түрде беруге болады. Олардың әрқайсысына сәйкес теңдеулері болады.
2. 1 Берілген нүкте арқылы өтетін, берілген векторға перпендикуляр жазықтықтың теңдеуі
O
xyz
кеңістігінде
 жазықтығы
жазықтығы
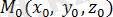 нүктесімен және осы жазықтыққа перпендикуляр
нүктесімен және осы жазықтыққа перпендикуляр
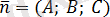 векторымен берілген.
векторымен берілген.
 жазықтығының теңдеуін қорытып шығарайық. Жазықтықтан кез-келген
жазықтығының теңдеуін қорытып шығарайық. Жазықтықтан кез-келген
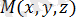 нүктесін алайық және
нүктесін алайық және
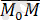 векторын құрайық.
векторын құрайық.
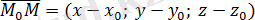
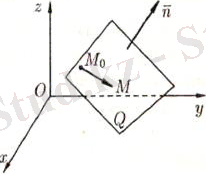
М нүктесі
 жазықтығында қалай орналассада
жазықтығында қалай орналассада
 және
және
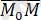 векторлары өзара перпендикуляр болады, сондықтан олардың скаляр көбейтіндісі нөлге тең:
векторлары өзара перпендикуляр болады, сондықтан олардың скаляр көбейтіндісі нөлге тең:
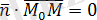 , яғни
, яғни
 жазықтығының кез-келген нүктесі (10. 2) теңдеуін қанағаттандырады, ал
жазықтығының кез-келген нүктесі (10. 2) теңдеуін қанағаттандырады, ал
 жазықтығында жатпайтын нүктелер қанағаттандырмайды. (10. 3) теңдеу берілген.
жазықтығында жатпайтын нүктелер қанағаттандырмайды. (10. 3) теңдеу берілген.
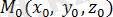 нүктесі арқылы өтетін,
нүктесі арқылы өтетін,
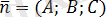 нормаль векторына перпендикуляр жазықтықтың теңдеуі деп аталады. x, y, және z координаталарына байланысты жазықтықтың теңдеуі бірінші дәрежелі болады.
нормаль векторына перпендикуляр жазықтықтың теңдеуі деп аталады. x, y, және z координаталарына байланысты жазықтықтың теңдеуі бірінші дәрежелі болады.
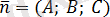 векторы жазықтықтың нормаль векторы деп аталады.
векторы жазықтықтың нормаль векторы деп аталады.
(2. 2) теңдеудегі
A
,
B
,
C
коэффициенттеріне мәндер беріп,
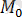 нүктесі арқылы өтетін кез-келген жазықтықтың теңдеуін алуға болады. Берілген нүкте арқылы өтетін жазықтықтар жиынын жазықтықтар байланысы деп, ал (2. 2) -жазықтықтар байланысының теңдеуі деп аталады.
нүктесі арқылы өтетін кез-келген жазықтықтың теңдеуін алуға болады. Берілген нүкте арқылы өтетін жазықтықтар жиынын жазықтықтар байланысы деп, ал (2. 2) -жазықтықтар байланысының теңдеуі деп аталады.
2. 2 Жазықтықтың жалпы теңдеуі
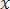 ,
,
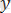 және
және
 үш белгісізді бірінші дәрежелі теңдеуді қарастырайық:
үш белгісізді бірінші дәрежелі теңдеуді қарастырайық:
Осы теңдеуді
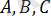 коэффициенттерінің бірдей нөлге тең емес болсын, мысалы, B
коэффициенттерінің бірдей нөлге тең емес болсын, мысалы, B
 0, онда (2. 2) теңдеуін былайша жазуға болады:
0, онда (2. 2) теңдеуін былайша жазуға болады:
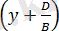 +C (z-0) =0
+C (z-0) =0
(2. 4) және (2. 2) теңдеулерін салыстырып, біз (2. 3) және (2. 4) теңдеулері
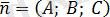 нормаль векторы бар.
нормаль векторы бар.
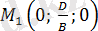 нүктесі арқылы өтетін жазықтықтың теңдеулері екенін көрініп тұр. (2. 3) теңдеуі O
xyz
координаталар жүйесіндегі қандай да бір жазықтықты анықтайды. (2. 3) теңдеуі жазықтықтың жалпы теңдеуі деп аталады.
нүктесі арқылы өтетін жазықтықтың теңдеулері екенін көрініп тұр. (2. 3) теңдеуі O
xyz
координаталар жүйесіндегі қандай да бір жазықтықты анықтайды. (2. 3) теңдеуі жазықтықтың жалпы теңдеуі деп аталады.
Жазықтықтың жалпы теңдеуінің дербес жағдайы
1. Егер
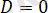 болса, онда жазықтық
болса, онда жазықтық
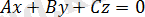 түрінде болады. Бұл теңдеуді O(0; 0; 0) нүктесі қанағаттандырады. Демек бұл жағдайда жазықтық координаталардың бас нүктесі арқылы өтеді.
түрінде болады. Бұл теңдеуді O(0; 0; 0) нүктесі қанағаттандырады. Демек бұл жағдайда жазықтық координаталардың бас нүктесі арқылы өтеді.
2. Егер
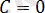 болса, онда жазықтық
болса, онда жазықтық
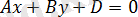 .
.
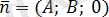 нормаль векторы
нормаль векторы
 осіне перпендикуляр болады. Демек, жазықтық
осіне перпендикуляр болады. Демек, жазықтық
 осіне параллель; егер
осіне параллель; егер
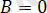 болса, онда
болса, онда
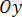 осіне параллель; егер
осіне параллель; егер
 болса, онда
болса, онда
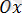 осіне параллель болады.
осіне параллель болады.
3.
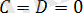 болса, онда жазықтық O(
0; 0; 0
) нүктесі арқылы өтіп
болса, онда жазықтық O(
0; 0; 0
) нүктесі арқылы өтіп
 жазықтығына параллель болады, яғни
жазықтығына параллель болады, яғни
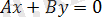 жазықтығы
жазықтығы
 осі арқылы өтеді. Тура осылайша
осі арқылы өтеді. Тура осылайша
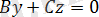 және
және
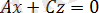 жазықтықтары сәйкес
жазықтықтары сәйкес
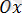 және
және
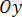 осьтері арқылы өтеді. p>
осьтері арқылы өтеді. p>
4. Егер
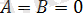 онда, (10. 3) теңдеуі
онда, (10. 3) теңдеуі
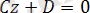 түріне келеді, яғни
түріне келеді, яғни
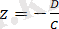 . Бұл O
xy
жазықтығына параллель жазықтық. Тура осылайша,
. Бұл O
xy
жазықтығына параллель жазықтық. Тура осылайша,
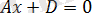 және
және
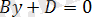 жазықтықтары сәйкес,
жазықтықтары сәйкес,
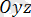 және
және
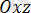 жазықтықтарына параллель жазықтықтарды анықтайды.
жазықтықтарына параллель жазықтықтарды анықтайды.
5.
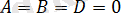 болса, онда (2. 3) теңдеуі
болса, онда (2. 3) теңдеуі
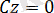 түріне келеді, яғни
түріне келеді, яғни
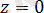 . Бұл
. Бұл
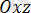 жазықтығының теңдеуі. Тура осылайша,
жазықтығының теңдеуі. Тура осылайша,
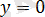 -
-
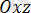 жазықтығының теңдеуі,
жазықтығының теңдеуі,
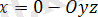 жазықтығының теңдеуі.
жазықтығының теңдеуі.
2. 3 Берілген үш нүкте арқылы өтетін жазықтықтың теңдеуі
Кеңістікте бір түзудің бойында жататын үш нүкте бір ғана жазықтықты анықтайды. Бір түзуде жатпайтын
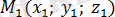 ,
,
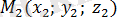 және
және
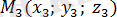 нүктелері арқылы өтетін
нүктелері арқылы өтетін
 жазықтығының теңдеуін табайық.
жазықтығының теңдеуін табайық.
Жазықтықтан қалауымызша кез-келген M( x; y; z ) нүктесін алайық және
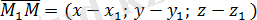 ,
,
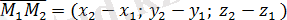 ,
,
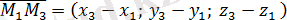
(2. 5)
векторларын құрайық. Бұл векторлар
 жазықтығында жатады, олар компланарлы векторлар. Векторлардың компланар шартын қолданып (олардың аралас көбейтіндісі нөлге тең),
жазықтығында жатады, олар компланарлы векторлар. Векторлардың компланар шартын қолданып (олардың аралас көбейтіндісі нөлге тең),
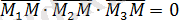 , аламыз, яғни
, аламыз, яғни
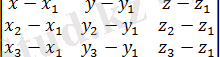 =0
=0
(2. 6) теңдеуі берілген үш нүкте арқылы өтетін жазықтықтың теңдеуі.
2. 4 Жазықтықтың кесінділер арқылы берілген теңдеуі
Жазықтық
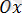 , Oy және
, Oy және
 осьтерін
осьтерін
 ,
,
 және
c
кесінділерін қияды, яғни ол
A(a; 0; 0), B(0; b; 0), C(0; 0; c)
нүктелері арқылы өтеді. Осы нүктелердің координаталарын (2. 5) теңдеуіне қойып, келесі анықтауышты аламыз
және
c
кесінділерін қияды, яғни ол
A(a; 0; 0), B(0; b; 0), C(0; 0; c)
нүктелері арқылы өтеді. Осы нүктелердің координаталарын (2. 5) теңдеуіне қойып, келесі анықтауышты аламыз
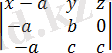 =0
=0
Анықтауышты ашып bcx-abc+abz+acy =0 аламыз, яғни bcx+acy+abz=abc немесе
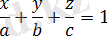
(2. 7) теңдеуі координаталар осьтеріндегі жазықтық кесінділер бойынша теңдеуі деп аталады. Бұл теңдеу жазықтықтарды салғанда қолданған ыңғайлы.
2. 5 Жазықтықтың нормаль теңдеуі
ОК=р
болсын, болсын онда
 бірлік векторының O
x
, O
y
, O
z
остерімен жасайтын бұрыштары
бірлік векторының O
x
, O
y
, O
z
остерімен жасайтын бұрыштары
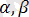 және
және
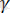 болады. Онда
болады. Онда
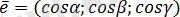 жазықтықпен кез-келген M(
x
;
y
;
z
) нүктесін алып, оны координаталар басымен қосайық. Сонда
жазықтықпен кез-келген M(
x
;
y
;
z
) нүктесін алып, оны координаталар басымен қосайық. Сонда
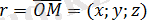 векторын аламыз:
векторын аламыз:
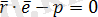
(2. 8) -теңдеуі векторлық формадағы жазықтықтың нормаль теңдеуі деп аталады.
 және
және
 векторларының координаталары белгісіз, (2. 8) теңдеуін
векторларының координаталары белгісіз, (2. 8) теңдеуін
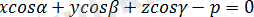
(2. 9) теңдеуі координаталық формадағы жазықтықтың нормаль теңдеуі.
(2. 3) жазықтықтың жалпы теңдеуін (2. 9) нормалдық теңдеуіне келтіруге болады, яғни (2. 3) теңдеудің екі жағында
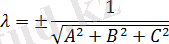
нормалдық көбейткішке көбейтеміз, мұндағы таңбасы жазықтықтың жалпы теңдеуінің D бос мүшесінe қарама-қарсы таңбасы алынады.
2. 6 Жазықтықтар. Негізгі есептері
Екі жазықтық арасындағы бұрыш. Екі жазықтықтың параллель және перпендикуляр болу шарттары
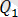 және
және
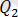 жазықтығы берілсін.
жазықтығы берілсін.
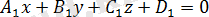 ,
,
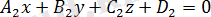 ,
,
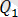 және
және
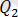 жазықтықтарының арасындағы бұрыш осы жазықтықтарынан құралған екі жақты бұрыш ұғымымен түсіндіріледі.
жазықтықтарының арасындағы бұрыш осы жазықтықтарынан құралған екі жақты бұрыш ұғымымен түсіндіріледі.
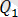 және
және
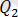 жазықтықтарының арасындағы бұрыш, осы жазықтықтардың
жазықтықтарының арасындағы бұрыш, осы жазықтықтардың
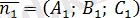 және
және
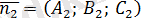 нормаль векторларының арасындағы бұрышқа тең. Сондықтан
нормаль векторларының арасындағы бұрышқа тең. Сондықтан
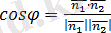 немесе
немесе
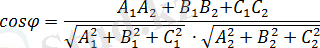
... жалғасы
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz