Деформация туралы

Жоспар

Мазмұны

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..4
1. Деформация туралы ұғым
1.1 Серпімді дене түсінігі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...5
1.2 Тартылу кезіндегі күштер және деформациялар ... ... ... ... ... ... ... ... ... ... ... ... 8
1.3 Деформацияланған денелердегі құбылыстар картинасы ... ... ... ... ... ... ... ...12
1.4 Материялдардың қасиеттері ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..14
1.5 Ішкі күштер және кернеу ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...15

2. Деформацияның түрлері және параметрлері
2.1 Серпімді денедегі кернеу. Жалпы жағдай ... ... ... ... ... ... ... ... ... ... ... ... ... ... 22
2.2 Дененің кіші деформациялары ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..29
2.3 Кернеулер мен деформациялар арасындағы тәуелділік ... ... ... ... ... ... ... ... .34
2.4Созылу иілу кезіндегі серпімділік модулін анықтау ... ... ... ... ... ... ... ... ... ... 42
2.5 Иілу кезіндегі серпімділік модулін анықтау ... ... ... ... ... ... ... ... ... ... ... ... ... 45
2.6 Айналу кезіндегі жылжу модулін анықтау ... ... ... ... ... ... ... ... ... ... ... ... ... ..46
2.7 Серпімділік модулін иілтіру әдісімен анықтау ... ... ... ... ... ... ... ... ... ... ... ... 47

3. Экперимент жасау

Қорытынды ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .55
Пайдаланылған әдебиеттер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .56

Пән: Физика
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 54 бет
Таңдаулыға:

Мазмұны

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... ... ... ... ..4
1. Деформация туралы ұғым
1.1 Серпімді дене
түсінігі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ...5
1.2 Тартылу кезіндегі күштер және
деформациялар ... ... ... ... ... .. ... ... ... ... ... ... ..8
1.3 Деформацияланған денелердегі құбылыстар
картинасы ... ... ... ... ... ... .. ... .12
1.4 Материялдардың
қасиеттері ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ... 14
1.5 Ішкі күштер және
кернеу ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ... .15

2. Деформацияның түрлері және параметрлері
2.1 Серпімді денедегі кернеу. Жалпы
жағдай ... ... ... ... ... ... ... . ... ... ... ... ... ... ...22
2.2 Дененің кіші
деформациялары ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ... 29
2.3 Кернеулер мен деформациялар арасындағы
тәуелділік ... ... ... ... ... ... . ... ... 34
2.4Созылу иілу кезіндегі серпімділік модулін
анықтау ... ... ... ... ... ... ... ... ... ... 42
2.5 Иілу кезіндегі серпімділік модулін
анықтау ... ... ... ... ... ... ... ... ... ... ... ... ... 45
2.6 Айналу кезіндегі жылжу модулін
анықтау ... ... ... ... ... ... ... ... ... ... ... ... ... ..46
2.7 Серпімділік модулін иілтіру әдісімен
анықтау ... ... ... ... ... ... ... ... ... ... ... ... 47

3. Экперимент жасау

Қорытынды ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .55
Пайдаланылған әдебиеттер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... . ... 56

Кіріспе

Физика-материя қозғалысының жалпы және қарапайым формаларын,

қасиеттерін зерттейтін ғылым.Әлемде, жер бетінде және жерден тыс нақты өмір
сүретіндердің баршасын ғылымда материя деп атайды.Физикалық шамалармен
тәжірибе жасау негізінде физикалық заңдар ашылады.Физикада анықталған
іргелі заңдардың өзінің күрделілігі мен орнықтылығы жөнінен кез келген
құбылыстарды зерттеу басталатын деректерден әлде қайда асып
түседі.Табиғаттағы әр бір нәрсе материялық қозғалыста болады.Бұл
қозғалыстар және сол қозғалыстардағы денелер бір біріне ұқсамайды .Оларға
әсер етуші күштер де өзгеше.Ньютон механикасы сонша зор құбылыстар класын-
денелер қозғалысын дұрыс сипаттаған, физика тарихында (тіпті жалпы ғылымда
( алғашқы тұтас, теория болды.Ньютон замандастары бұл теорияға қайран
қалды.Ньютон заңдары адамға қозғалысты тек зерттеп, біліп қана қоймай, оны
басқаруға да мүмкіндік береді.Бұл заңдар ешқашан да және ешбір жағдайда да
бұзылмайды.Сондай-ақ қазіргі физика электрондық есептеуіш машиналарын одан
әрі қарқынды дамудың, қимыл әрекет шапшаңдаудың және сенімділігін
арттырудың жаңа жолдары мен әдістерін ашып отыр.
Қазақстан Республикасының білімін дамытудың Мемлекеттік жоспарын ары
қарай іске асыру барысында және Қазақстанның білім жүйесінің функциясын
эффективті іске асыру үшін, Қазақстаның дүние жүзінің білім кеңістігінде
тианақты жоғарғы, орнында болуы Елбасы Нұрсұлтан Әбішұлы Назарбаевтің
дамыған елу елдің біріне айналу жоспарын жеделдетер деп сеніммен
қараймыз.Сондай – ақ қазіргі физиканың ғылыми техникалық ревалюцияға шешуші
үлес қосатынымызға да сеніміміз зор.

1.1 Серпімді дене түсінігі .

Күштің өзгеруіне байланысты дененің формасы өзгереді немесе
деформацияланады. Қатты денелердің механикасын оқу барысында біз, дене
деформациясын қозғалысқа аз әсер ететіндіктен ескермедік. Бірақ, көптеген
басқа есептерде мұның барлығын ескеруімізге тура келеді. Бұл таруда біз
денеге әсер ететін күштер және олар арқылы туындайтын деформацияларды
қарастыратын боламыз.
Ең алдымен біз мынаны ескеруіміз керек, яғни, денеге күш әсер
еткенде, ол тыныштықта ма әлде бірқалыпсыз қозғалыста ма, оған байланыссыз
дене деформацияланады. Мысалы: Сызғыштың екі ұшына оны тартатын тең және
қарама-қарсы күштер әсер етсін, бұл күштердің ұлғаюы барысында сызғыш
созылады, сызғыштың жеке бөлшектерінің арасындағы қашықтық та ұлғаяды,
сызғыш деформацияланады. Сызғыштың ұштарына түсірілген күштердің ұлғаюымен
барлық жеке бөлшектердің арасындағы қашықтық ұлғаяды.
Енді тура осы сызғыштың бір ұшына күш әсер етеді делік. Осы күштің
әсерінен сызғыш үдеумен қозғала бастайды, осы себепті де онда деформация
туындайды. Бірақ бұл жолғы деформацияның сипаттамасы басқа. Біріншісінде
деформация сызғыштың барық бөлігіне бір текті әсер етсе, екіншісінде
сызғыштың әр түрлі бөліктері әр түрлі деформацияланатын болады,сызғыштың
күш көп әсер ететін бөлігі көбірек деформацияланады.
Сызғыштың деформациялануын схема түрінде (1- суретте( көрсетілгендей
елестетуге болады, яғни пружина (серіппе) арқылы байланысқан массалар
түрінде модельдің соңғы массасына сырттан күш әсер еткенде,тізбек үдеумен
қозғалады; әр бір серіппеге әсер ететін күш бірінен – біріне өткен сайын
азаяды. Қандай-да бір серіппені тартатын күш барлық массаларға үдеу береді,
сондықтан да серіппелердің деформациялары әр түрлі болды. Осы себепті де
біртекті сызғыштың әр түрлі бөліктеріндегі тартылулар бірдей болмайды.
Деформацияланған дененің әр түрлі бөліктеріндегі күштер ішкі күштер немесе
күштену деп атайды.
Бұл мысалдар деформацияны талдау кезінде оның әсер ету сызығы бойынша
жылжытуға болмайтындығын көрсетеді. Деформация бірінші масса немесе үшінші
массаға күш түсірілу түсірілмеуіне байланысты әр түрлі болады.

(1-сурет)
Деформация түсірілген күштің немесе салмақтың өзгеруіне байланысты
өзгереді. Тұрақты күш әсер еткенде өзгеріссіз қалады.
Күштер мен деформацияларды біріктіретін заңдар өте күрделі, өйткені
әдетте күш пен деформация арасындағы байланыс біртексіз және түсрілген
күштің шамасына және сипатына байланысты.
Тек серпімді денеде және күш шамасының өзгеруінің белгілі диапазонында,
күштер деформацияны бірдей анықтайды немесе керісінше.Күш және деформацияны
байланыстыратын заңдылықтарды анықтау үшін біртекті өзектің (немесе
цилиндрдің) өз осі бойынша созылуы немесе сығылуы түріндегі қарапайым
деформацияны қарастырамыз. Ұзын болат өзектің немесе сымның созылу
тәжібелерінің нәтижесін қарастырамыз. (2-сурет). Егер өзектің материалы
біртекті болса, кез келген күште бірдей созылатын болады. Өзек ε
салыстырмалы ұзаю деп аталатын созылу деформациясымен сипатталатын болады:

(1)
мұндағы ( l1 - бастапқы l1- ұзындығы бар болған, өзектің кез келген
кесіндісінің ұзаюы. Кез келген кесінді үшін, сонымен бірге сым үшін де ε
шамасы бірдей болады және Ғ тарту күшінің шамасына тәуелді болады. Ғ
күшінің әсерінен өзекте ішкі күштер, күштенулер туындайды.Өзекті ойша
бірнеше бөліктерге бөлеміз және оның тепе-теңдік шарттарын қарастырамыз.

((-сурет( (3-сурет(
Тепе-теңдік шартынан бұл бөліктің ұштарына өзектің көрші бөліктерінен
әсер ететін күштер бір-біріне тең және қарама-қарсы екендігі шығады. Бұл
кез келген өзек кесіндісіне орынды болғандықтан, сәйкесінше өзектің кез
келген көлденең кесімінде Ғ –ке тең күштену туындайды.
Ғ күштенуді көлденең кесімнің бетіне түсірілген күш ретінде,
беттік күш ретінде қабылдауға болады. Егер материал бір текті болса,
күштену көлденең кесімнің жүзіне тең әсер етеді деп есептеуге болады.
Көлденең кесімнің ауданына әсер ететін күштенуді кернеу деп атайды және оны
( – мен белгілейді. Созылып жатқан өзекте туындайтын ( кернеу мынаған тең:
(=
(2)
мұндағы S-өзектің көлденең кесімінің ауданы. Тәжірибелердің көрсетуі
бойынша ε салыстырмалы деформация ( кернеумен анықталады.
Ғ тарту күшін немесе ( кернеуді жаймен көбейтіп отырамыз және өзектің
ұзаюын немесе ε салыстырмалы деформацияны өлшейміз. Осы тәжірибелерге
сүйене отырып 4-суретте көрсетілген ( кернеу мен ε салыстырмалы деформация
арасындағы тәуелділікті аламыз.
1.2 Тартылу кезінегі күштер және деформациялар.

Онша көп болмаған күштенуде ( кернеу және ε деформация шамамен бір-
біріне пропорционал болады. Осылайша П нүктесіне шейін созлады. Әрі қарай
деформация жылдам өсе бастайды да қисық ε деформация өсіне қарай иіледі, ал
Т нүктесінен бастап біраз бөлікте деформация өсіне шамамен параллель болып
барады – керену өспейді, ал деформация өседі. Қисық участкісіне сай
деформация (немесе кернеу) ауданы (Т-дан басталатын) ағымдық ауданы немесе
пластикалық деформация ауданы деп аталады.

((-сурет(
Әрі қарай, ε деформациясының өсуінен кернеу қисығы аздап ұлғаяды, Р
максимум нүктесіне жетеді, содан соң үзіледі. Қисықтың соңы өзектің
бөлінуіне сәйкес келеді; әрине тартушы күштің шамасы ( р – максималь
керенуге сәйкес келетін Ғ= ( р Ғ шамаға жеткенде бөліну болады.
( (ε) диаграммасын алып, тура осы материалдың жаңа үлгісін алып,
келесідегідей ретпен тәжірибелер жүргіземіз: үлгіге қайсы бір ( кернеуге
шейін салмақ түсіреміз. Содан соң біртіндеп салмақты азайтамыз, нәтижелерді
үзбей жазып отырамыз. Бұл тәжірибелердің нәтижелелері күш пен деформация
арасындағы біртекті тәуелділікті көрсетеді. Салмақ түсіру кезінде алынған (
(ε) қисығы салмақ алынғаннан кейінгісіне сәйкес келсе, деформация кернеуді
біртекті анықтайды және керісінше. Мұндай тәжірибелердің бірнешеуін орындап
көреміз,әрқайсысында максималь кернеудің мәнін үлкейтіп, содан соң азайтып
отырамыз. Тез арада біз ( у –дің бірнеше максималь мәнінен соң салмаққа
сәйкес келетін қисықтар, салмақ алынғаннан кейінгі қисыққа дәлме-дәл
түспейтіндігіне көз жеткіземіз. Тура сол мәндегі кернеуде салмақты алу
кезінде деформацияның үлкен мәнін аламыз, үлгіден салмақты мүлдем алып
тастаған кезде деформацияның мәні нөлге тең болмайды-өзекте, басқаша
айтқанда қалдық деформациялар туындайды.
0 бөлікке тура келетін кернеу мен деформацияның аз мәндеріндегі аудан-
берілген болат материалының серпімді деформациясының ауданы болып табылады.
ε у – ден кіші осындай деформацияларда, болат өзек созылу кезінде серпімді
дене сияқты болып қалады. ( п және ( т мәндерінің аралығында сыналып жатқан
материалды созу кезіндегі серпімділік шегіне сәйкес келетін нүктелер
жатады.
Берілген материал үшін серпімділік шегіне жетпейтін деформациялар
кезінде дене серпімді болып қалады. Тек қана серпімді деформациялар
аймағында немесе жай серпімді аймақта ғана кернеулер мен деформациялар
біртекті байланысқан.
4- суреттегі ( (ε) қисықтың бастапқы бөлігі түзу сызықты береді; бұл
бөлікте жобамен П нүктесіне дейін кернеумен деформацияның тәуелділігін тура
пропорционалдықтың қарапайым заңымен ұсынуға болады.

( = Е ( ε
(3)

бұл тәуелділікті Гук заңы деп аталады. Пропорционалдықтың тұрақты
коэффициенті Е Нм2 немесе Нмм2 пен өлшеніп, Юнг модулі деп аталады және
берілген материалдың тікелей сипаттамасы болып табылады. (көптеген
техникалық анықтамаларда Юнг модулі кгс мм 2 бірлікпен берлген). Гук заңы
орын алатын область пропорционалдық області деп аталады, ал ( п және ε п
деформация бағынатын шамалар пропорционалдық шектері деп аталады. Болат
үшін пропоционалдық шегі серпімділік шегіне жақын жатады, бірақ олар сәйкес
келмеулері де мүмкін.
Серпімділік шегінен кейінгі деформация-кернеу қисығының бөлігі
пластикалық деформация ауданы деп аталады, және мұндай деформациялар
кезінде дене серпімсіз болып табылады.
Егер деформация шамасын пластикалық деформация ауданына жататын
қайсыбір ε0 шамасына дейін жеткізіп, жүкті алатын болсақ, деформация шамасы
4-суретте көрсетілгендей біраз азаяды. Жүкті (салмақты) мүлдем алып
тастайтын болсақ қалдық деформация (0 тура ((0-нің мәніне жететін
болады.Қалдық деформациялар пластикалық ауданындағы бастапқы деформацияға
дерлік тең болады. Бұл оауданда әдетте екі түрлі нүкте қарастырылады:
ағымдық шегі (Т немесе ( т нүктесі) және беріктік нүктесі (Р немесе ( р
нүктесі). Ағымдылық шегіне жеткенде материал жұқара бастайды; бұл
салмақтың өспей, деформацияның ұлғаюын
білдіреді. ( р беріктік шегі – үлгі бұзыла қоймайтын максимальды кернеу;
бұл шектен асып кетсе үлгі бұзыла бастайды.
Созу және сығу кезіндегі деформациялар өте қарапайым. Өзектен ойша
бөлініп алынған куб, мұндай деформация кезінде параллепипедке айналады.
Бұдан кубтың көлденең қимасы да өзгереді, сонымен бірге өзектіңде көлденең
қимасы өзгереді: созу кезінде көлденең қима азаяды, ол сығылу кезінде
ұлғаяды, мұның барлығын тәжірибе жүзінд көру керек.
(5-сурет( (6-сурет(

Созу кезінде диаметрдің азаюын байқау өте оңай, алдын ала металл сақина
кигізілген резина түтікшені созу арқылы. Егер түтікшені вертикаль ұстап
тартатын болсақ, онда сақина біраз тартқан соң төмен түсіп кетеді. (5-
сурет).
Тәжірибелер өзектің көлденең қимасының азаюы ( ұзаю деформациясына
пропорционал. Егер кубтың көлденең шекарасын сақтап тұратын қабырғаның
салыстырмалы қысқаруын (п арқылы белгілейтін болсақ, онда

( п = μ (
(4)

мұндағы μ –ді көлденең сығу модулі немесе Пуассон коэффициенті деп аталады.
Көлденең сығу модулі Юнг модулі сияқты материалдардың серпімділік
қасиеттерін анық сипаттайды.
Қарапайым ойлаулардан соң мынадай пікірге келуге болады, яғни біртекті
изотроп материалдың көлденең сығу модулі μ12 болады.
Кубтың созлмай тұрғандағы көлемі а3 болсын. Егер кубтың қабырғалары
өзек өсіне паралель болса, онда деформациядан соң көлем мынаған тең болады.

а3*(1+() (1-( п) = а3 (1+() (1-μ () 2 = а 3 (1+(-2 μ ( + μ2 ( 2-2 μ (
2 + μ 2 ( 3) (5(

Созу кезінде көлем азаймайды, сондықтан

( (1-2 μ) + өте аз шамалар ≥0;
(6)

Бұдан (0 екендігін біліп, аз шамаларды ескермей мынаны аламыз.

( ≤ 12
(7)

1.3 Деформацияланған денелердегі құбылыстар картинасы

Деформацияланып жатқан денеде өтетін физикалық процесстер өте күрделі және
бұл облыстағы көптеген сұрақтар осы уақытқа дейін зерттелмеген.
Жоғарыда айтылған құбылыстардың барлығы металлдарға тиісті.
Рентгеноскопиялық зерттеулер көрсеткендей жай жағдайда металлдар бір-
бірінен салыстырмалы түрде кіші, әртүрлі орналасқан ұсақ кристаллдардың
жиынтығын береді. Кристаллдарда атомдар кристалл торлардың бойымен,
реттілікпен орналасқандығы белігілі. Мысалы алюминийдің кристалл торы бір-
біріне жанасып тұрған,бірдей ұяшықтардың жиынтығынан тұрады. Әр бір ұяшық
кубтәріздес болып, бұрыштарына атомдар орналасқан, және әр куб қырының
центрінде бір атом орналасады. Кристалл торлардың мұндай құрылымы
ценрленген қырлы куб торлар деп аталады.
Әрине, егер материалдың үлгісі толығымен тек кристаллдан
(монокристаллдан) тұратын болса, онда оның әр бағыттағы серпімдлік
қасиеттері әртүрлі болады. Мұндай денелер анизотропты денелер деп аталады.
Ал шын мәнінде ұсақ кристаллдар хастикалық түрде орналасқан және бір-біріне
салыстарғанда әртүрлі бағытта бағытталған (7- сурет).
Сондықтан металлдың серпімділік қасиеттері әр түрлі бағытта да бірдей және
металл изотропты дене болып табылады. Пластикалық деформация кезінде
монокристаллдардың кейбір белгілі жазықтық маңында сырғанауы байқалады.
Кристалл бөлшектер мұнда сырғанау жазықтықтарында бір-біріне қатысты оңай
қозғалады және осы жағдайда (қалыпта) салмақ, алынған сонда қала береді.
Пластикалық деформация кезінде денені құрайтын ұсақ кристаллдар да осы
процесс жүреді.

Металлдағы деформация картинасын былайша елестетуге болады. Серпімді
деформация аймағында кристаллдар қозғалмай және бұзылмай өздерінің
формаларын өзгертеді. Салмақ алынған соң олар өздерінің бастапқы
қалыптарына келеді. Пластикалық деформация аймағында кристаллдар формаларын
(пішіндерін) жоғалтып қана қоймай бір-біріне қатысты сырғанап, сынады да.
Бұл өзгерістер салмақ алынған соң да өз қалпына келмейді, дене
деформацияланған дене болып қала береді де, онда қалдық деформациялар
туындайды.
Пластикалық деформациялардың технологияда алатын орны көп: пластикалық
деформациялардың арқасында металлдардан құйма бұйымдар, ию, штамповка жасау
мүмкіндігі туып отыр. Егер металл тек серпімді деформациялы болғанда,
аталған тәсілдер арқылы металлдан еш нәрсе істеу мүмкін болмас еді.
Мынаны ескеруіміз керек, яғни пластикалық деформация күйіне
жеткізілген және салмақ түсірілген үлгі, деформациядан соң өзгертілген
серпімді қасиеттерге ие болады. Егер тағы да салмақ түсірсек,
пропорционалдық шегі ұлғаятындығын көреміз. Мысалы, болат сымды жасар
алдында, оның беріктігін арттыратын өңдеу жүргізіледі. Металлдар және басқа
материалдардың механикалық қасиеттерін белгілі тәсілмен өңделген және
белгілі өлшем мен пішіні бар өзекті созу арқылы анықталады. Созуды
гидравликалық пресс принципі бойынша жұмыс істейтін арнайы машиналарда
амалға асырады.

(8-сурет(
1.4 Материялдардың қасиеттері

Поршень цилиндріндегі қысымнан тартушы күшті анықтайды, ал дәл прибормен
өлшенген поршеннің қозғалуы стержень деформациясын анықтауға мүмкіндік
береді. Принципінде тура осындай әдіспен өзекті сығу кезіндегі деформация
мен кернеудің тәуелділігі анықталады, ол үшін өзекті қысқа және жуан етіп
алады. Металлдар үшін Юнг модулі сығу кезінде де созу кезінде де бірдей
болып қалады. 9 а –суретте кәдімгі болат үшін деформация –кернеу қисығы
сипатталған. Сығу кезінде пропорционалдық шегі созуға қарағанда басқа мәнге
ие болады және пластикалық деформация аймағындағы қисық сәл басқаша болады.

Басқа материалдар үшін кернеу-деформация қисығы тіпті басқаша түр
алады. Мысалы: 9 б – суретте шойын үшін осы қисық көрсетілген. Созу кезінде
шойынның пластикалық деформация аймағы болмайды. Серпімділік шегіне
жеткенде білінер-білінбес ағымдылық аймағы басталады да үлгі бұзыла
бастайды. Мұндай материалдар морт материалдар деп аталады, олардың иілгіш
материалдарға қарағанда пластикалық деформация аймағы аз болады.
Иілгіш және морт материалдардың қасиеттеріндегі мұндай айырмашылықтарды
білу практикада өте қажет болады. Егер иілгіш материалдан жасалған машина
жұмыс істеп жатқанда керену кейбір жерлерде серпімділік шегінен өтетін
болса машина бұзылмайды,ал машина морт материалдан жасалған болса, істен
шығады.Сығу кезінде шойында дерлік пропорционалдық аймағы болмайды, Е-нің
өте аз мәндерінде де кернеу-деформация тәуелділігі сызықты емес болады. 9 в-
г – суретте кейбір материалдар үшін кернеу-деформация тәуелділігі
көрсетілген.Мәрмәр, бетон сияқты морт материалдар техникада созуға
қарағанда сығуға шыдамды болады, яғни сығу кезінде беріктік шектері созу
кезіндегіге қарағанда жоғарлау болады.

(9-сурет(

Материялдардың серпімді қасиеттерін білген жағдайда ғана төзімді
машина,құрап және басқаларды құруға болады.

1.5 Ішкі күштер және кернеу

Сыртқы күштер әсер етіп тұрған кез келген қатты денедегі күштену мен
кернеуді былайша қарастырған оңай: дененің кез келген бөлігін бөліп аламыз.
Бұл бөлініп алынған бөлшекке дененің басқа бөліктерінен күш әсер ете
бастайды, немесе бөлініп алынған бөлшектің бетінде кернеу болады. Кернеулер
белгілі бір шарттарға бағынады, яғни осы бөлініп
алынған бөлшекке әсер ететін күштер дене тыныштықта тұрғанда нөлге тең
болуы керек немесе бөлшектің массасы мен оның қозғалысы кезіндегі үдеудің
көбейтіндісіне тең болуы керек, сонымен бірге бұл күштердің моменттеріне де
қатысты өте орынды шарттар бар. Егер күштер мен моменттердің проекцияларын
үш координата остері бойынша қарастыратын болсақ, берілген бөлшекке әсер
ететін күштерді қанағаттандыратын алты теңдеуді аламыз: үшеуі –күштердің
проекциялары үшін, үшеуі –үш осьтің айналасындағы моменттер үшін. Бұл
шарттар деформациядан мүлдем тәуелсіз және серпімді аймақта да, пластикалық
деформация аймағында да бірдей болып келед.
Біртекті өзекті созған кездегі кернеуді қарастырамыз. Ойша осы
өзектен оның өсіне перпендикуляр етіп призма пішіндес бөлшек кесіп аламыз.
Сонда призманың төрт қырындағы кернеу нөлге тең болады да, тек негізіндегі
кернеу (0, қарама қарсы бағытталған және негізге нормаль. Олар мынаған тең:
( 0 =
(8)
мұндағы Ғ-көлденең қимадағы күштену, ал S- көлденең қиманың ауданы. Егер
өзек біртекті болса, онда (0 кернеу бүкіл көлденең қима үшін бірдей және
өзек тыныштықта тұрғандағы кез келген көлденең қима үшін бірдей болады.

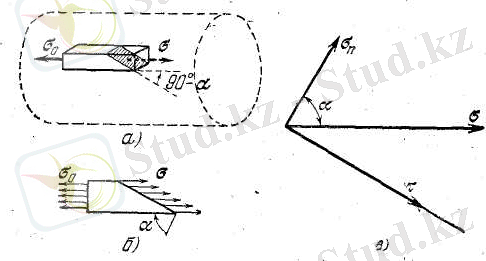
(10-сурет(
Жалпы жағдайда қатты денедегі кернеу өзі жатқан участкіге қандай да
бір бұрышпен бағытталған болады. Біздің жағдайымызда бөлініп алынған
бөлшекті мүлдем басқаша елестетуге болады, мысалы призманы жазық бойлап
кесіп алған соң, оған жүргізілген нормаль мен өзек осінің арасында α бұрыш
пайда болатын етіп. Сонда призманың көлденең кесіміндегі ( (0 –ге тең
болмай қалады, ал ( өзектің осіне 900 бұрышпен бағытталған болады. (
кернеудің шамасын кесіп алынған бөлшектің тепе-теңдік шартынан анықтаймыз.
Бұдан көретініміз, бөлшекке әсер ететін күштер тепе-тең және қарама-қарсы,
бұдан.

( 0 S = (
немесе
( = (0 cos (
(9(

мұндағы S-призманың нормал қимасының ауданы ( кернеудің қима жазықтығына
нормаль құраушысы ( п және тангенциял құраушысы ( бар (10,в сурет(.Нормаль
құраушысына тең
( п = ( cos ( = ( 0 cos 2 (
(10(

ал тангенциаль құраушысы:
( = ( sin ( = (0 cos ( sin (
(11(

Олар қима ауданының нормалімен өзек осінің арасындағы ( бұрышқа
тәуелді.Қима ауданын ( бұрыштыңәр түрлі мәндерінде алып және (9(,(10( және
(11( формулаларына сәйкес кернеудің әр түрлі мәндерін аламыз.Аудан мен өзек
өсінің арасындағы бұрыш 450 болғанда тангенциалды құраушының мәні (02-ге
тең, ең үлкен көрсеткішті береді; әрине,бұл жағдайда нормаль құраушының да
сондай болады.(11-сурет(

(11-суерет(

Осыдан қатты дененің созылу процесі өте күрделі екендігін көруге болады.

2.Деформацияның түрлері және параметрлері

Жылжу кезіндегі таза деформацияны, мысалы, біртекті дөңгелек өзекті
(стерженді) айналдыру кезінде, өзектің бір негізі басқа бір негізіне
қатысын φ бұрышпен өз осінің маңында айналғанда көруге болады. Бұл кезде
пайда болатын деформацияны алдын ала ортоганалды сызықты тор кигізілген
резина түтікті айналдыру арқылы көруге болады. Мұндай айналдыру кезінде
цилиндрдің шеңбері бойымен сызықтар пішімдерімен жоғалтпайды, ал ось
бойымен орналасқан сызықтар винт тәріздес пішінге енеді. (12, а-б сурет).
Түтікшені ойша айналу кезінде винттік (бұрғылық) сызықтың кесімін
дисктің ішінде тура деп есептеуге
болатындай етіп, жұқа дисктерге бөлеміз. Дисктен сақина, ал сақинадан
кішкене куб бөліп аламыз. (15, б-сурет). Диск өте жұқа болғандықтан
түтікшенің деформациясы кезінде кубтың жоғарғы қыры төменгісіне қарағанда
жылжиды (бүйір қырлары қисаяды), бүйір қырларымен төменгі қырларының
арасындағы бұрыш түзуден айырмашылығы бар болып қалады. Кубтың деформациясы
жылжудың таза деформациясы болып табылады, мұнда тек параллелепипедтің
бұрыштары ғана өзгереді.

(12-сурет(
Жылжу деформациясы параллелепипед қырларындағы жанама кернеулерден ғана
туындайды. Қабырғалары 1 см болған, төрт қырына жанама күштенулер қойылған
кубты алайық (13 а - сурет).

(13-сурет(
Кубтың тепе-теңді шартын ескере отырып, барлық жанама кернеулер
мынаған тең дейміз:
(1 = (2 = (3 = (4 = (

Жанама күштенулердің әсерінен кубтың сәйкес қырларының арасындағы
бұрыштар ( кіші бұрыштарына азаяды. (13, б-сурет). ( бұрышпен анықталатын
куб деформациясының шамасы заңды түрде кубтың сәйкес қабырғаларындағы (
жанама кернеулердің шамасымен байланысты. Берілген материал үшін ( және (
арасындағы байланыс, тура сол материал үшін ( және ( арасындағы
тәуелділікпен бірдей (14 - сурет).Серпімділік аймағында сызықтық участка
бар, онда
(= G(
(12)

G коэффиценті жылжу модулі деп аталады, және Нм2 өлшем бірлікпен өлшенеді.

(14-сурет(

Енді дөңгелек қималы өзекті айналдыру кезінде туындайтын деформациямен
күштенуді қарастырамыз; бұл деформацияларды біз жоғарыда аздап қарастырдық.
Өзектің ұзындығы l0,диаметрі D болсын да жылжу модулі G –ға тең
материалдан жасалған болсын және (0 бұрышқа М моментпен айналдырылған
болсын. Кез келген қимадағы ішкі күштер моменті өзекті айналдыратын күш
моменті М3-ке тең болады.
Ойша кесіп алынған өзектің В бөлігін қарастырамыз (15, а - сурет);В
тыныштықта тұрғандықтан күш моменті нөлге тең болады.

(15-сурет(
Бұл бөлікке бір ұшынан сыртқы күштердің моменті М3, ал екінші ұшынан
қимаға жанама ішкі күштердің моменті М әсер етеді.
Одан әрі өзек қимасындағы жанама кернеулер қалай тарағандығын және
деформациямен қалай байланысқандығын анықтаймыз. Қозғалмайтын негізден l
қашықтықтағы dl өте аз биіктікті дискті өзектен қырқып аламыз да,бұл
дисктің төменгі негізгі ( бұрышқа, ал жоғарғысы (+d( бұрышқа бұрылды
делік. Бұл дисктен ішкі радиусы г ал сыртқы радиусы r +dr сақина қиып
аламыз (15, б –сурет). Сонда сақинадан қиып алынған кубтардың жылжу
деформациялары бірдей болады, яғни барлығы dα бұрышқа бұрылады. Дисктің
жоғарғы негізгі төменгі негізіне салыстырғанда, деформацияланбай d( бұрышқа
бұрылса, онда жылжу бұрышы dα сақина радиусы г-ге пропорционал. Сақинаның
жоғарғы негізінің төменгі негізіне қарағанда жылжуы маныған тең
dа = dl d( = r d(.
( 14)

Сондықтан жылжу бұрышы

d( = r ,
(15)

немесе сақинаның жылжу бұрышы сақинаның радиусымен айналдыру бұрышынан
өзектің ұзындығы бойынша алынған туындыға көбейтіндісіне тең . Енді ауданы
2(rdr болған сақинаның беттік жазықтығындағы жанама күштенуді анықтаймыз;
(13) және (15) формулалары бойынша кернеу ( мынаған тең:

( = Gd( = Gr
(16)

сондықтан сақина бетіндегі күштену

((2(r dr =
(17)

өзек осіне қатысты күштенудің моментімынаған тең:

d(=
(18)

Енді диск бетіндегі күштену моменттерін қосамыз немесе (18) формуланы r
бойынша интегралдаймыз:

(=
(19)
Бұл момент өзекті айналдыратын М3 моментке тең болуы керек, әйтпесе бір-
біріне табыстырылған екі дисктегі моменттер бір-біріне тең.
(19) теңдеу егер өзек біртекті болса,онда өзекті айналдыру бұрышының
туындысы өзек бойында тұрақты болып қалады.Бір-бірінен l0 қашықтықта
орналасқан өзектің дөңбек қимасыныңайналу бұрышы мынаған тең

(0= , немесе =
(20)

(20) өрнекіті (19) формулаға қойып,(0 бұрыштың М3 моментке тәуелділік
формуласын аламыз:

М3= (0=
(21)

(D4G32l0 шама айналу кезіндегі өзек қатаңдығының коэффициенті деп аталады.

2.1 Серпімді денедегі кернеу. Жалпы жағдай

Алдынғы қарастырылған мысалдар әр түрлі аудандарда әр түрлі кернеулер
болатындығын, бірақ олар бір-бірімен байланысты екендігін көрсетеді. Жалпы
жағдайда, кез келген салмақты мүмкін болған кернеулердің жиынтығы нүкте
қиылысында екінші рангтың симметриялық тензорының компоненттерін беретін
алты шамамен анықталады. Кернеу және басқа да физикалық шамаларды
сипаттауда тензорларды қолдану өте ыңғайлы.
Әр түрлі берілген нүктеден өтетін кернеулердің өзара байланысын
көрсету үшін, осы нүктенің маңайындағы денеден кесіп алынған шексіз кіші
тетраэдрдың тепе-теңдігі қарастырылады. Дененің қарастырылып отырған
нүктесінде тік бұрышты координаталар жүйесінің басы орналасқан делік (16-
сурет), оларды 1,2,3 деп және осы осьтердің векторларының проекцияларын
сәйкес цифрлық индекстермен белгілейміз. Нормаль ( бірлік векторымен
белгіленген аудан, О нүктесінің маңынан өтіп, координаталық жазықтармен
бірге АВСО тетраэдрін құрайды.

(16-сурет(
Бұл тетраэдрдың қырларына дененің қалған бөліктерінен күштену әсер етеді.
dS тең АВС қырының ауданы 1- оське нормаль қыр ауданы dS1 – мен мынадай
теңдікпен байданысқандығын ескертеміз.: dS1=(1dS, мұндағы ν1- ν мен 1-ось
арасындағы бұрыш косинусы. Осыған сәйкес, dS2= ν1dS және dS3= ν1dS;
мұндағы dS1, dS2 және dS3 1,2 және 3 осьтерге сәйкес тетраэдр қырларының
ауандары. dS аудандағы күштенулерді (( dS арқылы белгілейміз. (( - осы
аудандағы кернеу (вектор(.

(17-сурет( (18-сурет(
Әдетте созылатын нормаль кернеулер оң, ал сығатындары-теріс болып
есептелінеді. Координаталық жазықтықтардағы аудандардың оң жағы деп ось
үшін бағытталған жағын айтады, бұл осьтің бірлік векторы терістен оңға
бағытталған. dS ауданның оң жағы тетраэдрдің сыртында жатады. (17- сурет).
Тетраэдр бетіне әсер ететін күштердің тепе-теңдігі мынадай жағдайда орын
алады.

(( dS - (1dS1 - (2 dS2 - (3 dS3 = 0
(22(

(бұл жерде кернеулердің таңбалары ескеріледі(.
Көрнекілік үшін 18-суретте барлық күштенулер (1,2( жазықтықтарға паралель
болатын (жазықтық( жағдайында күштену векторларын көрсетеміз;бұл жағдайда
тетраэдрдің орнына призманы алуға болады, ал векторлардың барлығы
жазықтықта жатады. (22( теңдеу бұл жағдайда мынадай түрге енеді.

(( dS - (1 dS1 - (2 dS2 = 0

Тетраэдрдің іші үшінші ретті, ал сырты екінші ретті шексіз кіші шама
болғандықтан, оның ішіндеі бөлшектерге түсірілетін заттың тығыздығына
пропорционал күштерді ескермеуге болады.
Егер (22) теңдікті dS –ке бөлетін болсақ, ол мынадай түрге кіреді.

(( = (1 (1 +(2 (2 +(3 (3
(23)

мұндағы (1, (2, (3-нормальді dS ауданға бағыттаушы косинустар. Бұл өрнек
түріне қарай келесі өрнекке сәйкес келеді.
а( = (1 а1 + (2 а2 + (3 а3 = (а

Бұл өрнек вектордың анықтамасын береді. а1, а2, а3 – векторлар
проекцияларын-скалярлар. Координата осіне түсірелітін 3 проекцияны біле
отырып ( кез келген бағыттағы вектор проекциясы анықталады.
(23)формула екінші рангтың тензорын анықтау үшін қолданылады: (1, (2,
(3 үш вектор (( -векторын-кернеуді анықтайды.Координата осьтеріне нормаль
үш аудандағы үш кернеу вектор белгі болса,онда (нормальді аудандағы кез
келген кернеуді анықтауға болады.Үш вектор тоғыз санның-осы векторлардың
координата осьтеріндегі проекцияларының жиынтығын береді.(1, (2, (3
векторларын компоненттерде жазамыз:
(1 = (11е1 + (21е2 + (31е3;
(2 = (12е1 + (22е2 + (32е3;
(24)
(3 = (13е1 + (23е2 + (33е3;
Индекстердің ретіне назар аударыңыз:біріншісі-ось номері,екіншісі-ауданның
номері е1, е2, е3 - 1,2,3 координата осьтерінің сәйкес бірлік векторлары.
Бірдей индексті координаталар: (11, (22, (33 - кернеу ауданына
түсірілгеннормальдар,әр түрлі индекстілер; (12, (31,... - жанама
кернеулер.
(24)-тегі (1, (2, (3 векторларының мәндерін (23) теңдеуге қойып
көреміз,содан соң оны біртіндеп е1, е2, е3-ке көбейтіп шығамыз,осьтердің
ортаганальдығын ескере отырып (егер і=k болса, еі еk=1,және і(k болса, еі
еk= 0).Барлығын орнына қойып болған соң келесі теңдеуді аламыз:
(1( = (11 (1 + (12 (2 +
(13(3;
(2( = (21 (1 + (22 (2 +
(23(3; (25)
(3( = (31 (1 + (32 (2 +
(33 (3;

Бұл теңдіктер жүйесін Г тензордың көмегімен былайша жазуға болады.
((=Г(
(26)

яғни, аудандағы ( нормальды кернеу векторы Г тензордың ( нормаль векторына
көбейтіндісіне тең. Г тензор мына матрица арқылы беріледі:
(11 (12
(13
Г= (21 (22 (23
(27)
(31 (32 (33

координата осіндегі вектор проекциялары (1, (2, (3 оның компоненттері
болып табылады. Байқаған болсаңыз. (23), (25) және (27) формулалары бір
ұғымды өрнектейді.
(25) және (26) тегі (ік компонентерінің жазылуына назар аударыңыз.
Координаттар жүйесін түрлендіру кезінде (ік тензорының компоненталары хіхк
сәйкес координата нүктелерінің көбейтіндісі түрінде түрленетіндігін
көрсетеді. Бұл (ік сандарының жиынтығы тензорды беретіндігін білдіреді.

(18-сурет(
(22) шарт өте қажет, бірақ АВСО тетраэдрдің тепе-теңдігі үшін
жеткіліксіз. Тетраэдрдің жазықтығына кез келген оське қатысты әсер ететін
барлық күштердің моменттерін талап ету керек. Оңайлату үшін dS ауданының
ауырлығының центрінен өтетін және үшінші координаталық оське параллель
оське әсер ететін күштердің моменттерінің нольге теңдігін қарастырамыз. dS
өте аз аудан болғандықтан кернеуді тұрақты деп аламыз, сондықтан әр бір dS
аудандағы күштенудің тепе-тең әсер етушісі ауданның ауырлық центріне
түсірілген. 18-суретте 3 ось бойынша тетраэдрдің жоғарыдан қарағандағы түрі
көрсетілген. Таңдалынған ось (18 суретте с нүктесі) dS3 ауданынан
өтетіндігін байқау қиын емес, сондықтан (( dS және (3 dS3 күштенулер осьтен
өтеді және момент бермейді. (1 dS1 және (2dS2 күштенулердің моменттерін
қарастыру қалды. Бұдан
(21 - dS1 h1 - (12 - dS2 h2 = 0

мұндағы h1 және h2 - dS1 және dS2 аудандары мен мен с осінің арасында
қашықтық. Егер тетраэдрдің а1, а2, а3 қабырғалары әр бір ось бойынша
бағытталған болса, онда dS1=12 а1 а2, dS2=12 а1 а3 Осыны және а1 = 3h2,
а1 = 3h1, екендігін ескере отырып, мынаны табамыз

(12=(21
(28)

3 – оське нормаль dS1 және dS2 аудандардың жанама кернеулерінің
компоненттері, осы осьтің ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.