ЕМЕС, НЕМЕСЕ және ЖӘНЕ логикалық операцияларының теориясы мен цифрлық құрылғылардағы қолданылуы


Алматы қ. Білім басқармасы
«Халықаралық бизнес және коммуникация колледжі» мекемесі
1306000 - Радиоэлектроника және байланыс мамандығының
___2__ курс ___ 206__ топ студенті
« Илияс Жанел Уланкызы »
(студенттің аты-жөні, тегі)
курстық жұмысы
Байланыс желісінің қондырғылары
(пәннің атауы)
Негізгі логикалық операциялар «ЕМЕС НЕМЕСЕ ЖӘНЕ»
(курстық жұмыстың тақырыбы)
Тексерген: Джамбаев Д. К.
Алматы 2021
Мазмұны
3. 3 Қиыстырма құрылғыларды құру тәртібі
3. 4 Шифраторлар
3. 5 Микропроцессордың үзіліс жүйесі
13
14
17
Қорытынды
Қолданылған дерек көздері
20
21
Кіріспе
Әртүрлі деңгейдегі жиналымды микросхемалар арқылы жүзеге асырылатын цифрлық құрылғылар мен цифрлық өңдеу тәсілдері заман талабына сай (әртүрлі) құралымдардың негізін қалайды. (Бұл осы мәселелерге байланысты маманданушы студенттердің цифрлық құрылғылар жөнінде жеткілікті Деңгейде білім алуын қажет етеді. ) Оқу құралының мақсаты - студенттердің цифрлық құрылғылар мен микропроцессорлардың құрылым принциптері және олардың жұмыс тәртібі жөніндегі білімін қалыптастырып, олардың оқу барысының келесі кезеңдерінде оқытылатын арнайы пәндерді (мысалы, Микропроцессорлық жүйелер, Бағдарламалы құрылымдар және т. б. ) игеруіне немесе өздік жұмыс арқылы білім деңгейін көтеруіне қажетті түпнегіз қалау. Оқу құралының бірінші бөлімінде цифрлық құрылғылардың математикалық (арифметикалық және логикалық) негіздері, қиыстырма және тізбектеме құрылғылардың құрылу тәртібі мен іс-әрекеті және олардың қалыпты түрлері, жады құрылғыларының негізгі құрылым принциптері мен кеңейтілу жолдары қарастырылған. Оқу құралының екінші бөлімі, жалпы түрде микропроцессорлық жүйе (МПЖ) деп аталатын, есептеу, бақылау-өлшеу және басқару жүйелерінің құрамындағы басты құрылғысы саналатын, микропроцессорлардың құрылымымен, олардың іс-әрекеттерінің ұйымдастырылу тәртібімен таныстыруға арналған. Микропроцессорлардың негізгі құрылым принциптері мен жұмыс тәртібін түсіндіру үшін олардың нақтылы бір түрін қарастыру ыңғайлы келеді. Оқу құралында осындай үлгі ретінде осы заманның басқару жүйелерінде кең қолданылатын қарапайым микропроцессор Intel 8085 алынып, оның ішкі құрама блоктары мен іс-әрекетін басқарушы бағдарламаларының құрылу негіздері қарастырылды. Микропроцессорлық жүйелерге байланысты материал оқу құралының екі бөлімін ұштастыру мақсатында және микропроцессорлардың құрылымы мен жұмыс тәртібін қарастыруға кіріспе ретінде енгізілген. Оқу құралы автордың өндіріс және педагогика саласындағы көпжылдық тәжірибесінің негізінде жазылды. Мазмұны жағынан оқу құралы бакалаврлық оқу жүйесінде 050704 - Есептеу техникасы және бағдарламалы қамтамасыздандыру және 050719 - Радиотехника, электроника және телекоммуникациялар мамандықтарына дайындау барысында оқытылатын “Цифрлық құрылғылар және микропроцессорлар” пәнінің бағдарламасына сәйкес келеді. Айтылған мамандықтармен қатар оқу құралын (сәйкесті қысқарту немесе толықтыру арқылы) өзге мамандықтарға жоспарланған осы сияқты пәндерді оқыту барысында пайдалануға болады.
1. 1 Екілік санау жүйесі
Цифрлық құрылғыларда пайдаланылатын екілік санау жүйесі позициялық санау жүйесіне жатады. Демек, сандарды екілік санау жүйесінде көрсету үшін және оларға арифметикалық операциялар жүргізу үшін, өзімізге таныс, күнделікті пайдаланылатын ондық санау жүйесінің қағидалары пайдаланылады. Сондықтан, алда келтірілетін, екілік санау жүйесіне байланысты түсіндірмелер ондық санау жүйесіндегі сәйкесті мәселелерді еске түсіріп, салыстырма қарастырылым арқылы жүргізіледі.
Ондық санау жүйесінде сан жазуға он символ (0 … 9) пайдаланылады (бұл жүйенің ондық санау жүйесі деп аталуы да осыған байланысты) . Бұл символдардың сандағы тұрған орнына байланысты құны (салмағы) белгіленеді: ол онның (яғни, санау жүйесінің негізінің) сәйкесті разряд нөмірінің мәніндегі дәрежесі арқылы анықталады. Сонымен, санның ең кіші разрядындағы (нөлінші разрядтағы) символдың құны бір (100), келесі разрядтың (бірінші разрядтың) құны он (101), одан әрі жүз (102), мың (103) және с. с. өзгере береді. Разряд құны, мәніне сәйкесті, бірлік, ондық, жүздік, мыңдық деп және с. с. аталады, ал сан разрядында тұрған символ сәйкесті разряд құнының сан құрамына қанша рет кіретіндігін көрсетеді. Келесі мысал арқылы айтылғанды түсіндірейік:
Сонымен, келтірілген санның құрамында 7 бірлік, 5 жүздік, 3 мыңдық бар, ал ондық жоқ (0) .
Екілік санау жүйесінде сан жазуға екі символ (0 және 1) пайдаланылады. Разряд құны екінің (яғни, санау жүйесінің негізінің) сәйкесті разряд нөмірінің мәніндегі дәрежесі арқылы анықталады. Сонымен, санның ең кіші разрядындағы (нөлінші разрядтағы) символдың құны бір (20), келесі разрядтың (бірінші разрядтың) құны екі (21), одан әрі төрт (22), сегіз (23) және с. с. өзгере береді. Разряд құны бірлік, екілік, төрттік, сегіздік деп және с. с. аталады, ал екілік код разрядында тұрған символ сәйкесті разряд құнының сан құрамына қанша рет кіретіндігін, дәлірек айтқанда, бар-жоқтығын көрсетеді. Айтылғанды келесі мысал суреттейді:
Код құрамындағы символдардың 0 және 1 мәнінде ғана болуына байланысты, олар разрядқа сәйкесті құндық мәннің код құрамында бар-жоқтығын көрсетеді. Мысалы, келтірілген мысалдағы кодтың құрамында бірлік, екілік және сегіздік бар (1), ал төрттік жоқ (0) .
1. 2 Ондық санның екілік санға түрлендірілуі
Өзімізге үйреншікті ондық сан түріндегі информацияны цифрлық құрылғыда өңдеу үшін ол екілік санау жүйесіндегі сәйкесті көрсетілім түріне, яғни екілік кодқа түрлендірілуі керек. Ол үшін түрлендірілетін сан және алынған кезекті бөлінділер екіге (яғни, жаңа санау жүйесінің негізіне) тізбелеп бөлінеді де, бөлінді мәні нөл болған кезде бөлу операциялары тоқтатылады; жеке бөлу операцияларында анықталған қалдықтардың шығарылым бағытына қарсы тәртіппен жазылымы осы ондық санның екілік кодын береді. Мысал ретінде, ондық санау жүйесіндегі 75 санына сәйкесті екілік кодтың анықталуын көрсетелік:
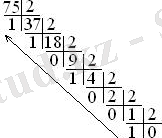
Сурет1. 1 -Санау жүйесіндегі 75 санына сәйкесті екілік кодтың анықталуы
Әрине, көрсетілген тәсілмен кез келген ондық санның сәйкесті екілік кодын анықтауға болады. Бірақ автор бұл тәсілді жеңіл тәсіл деп санамайды: біріншіден, бұндағы тізбелеп жүргізілетін бөлу операциялары ұзақ уақыт алады (мысал ретінде ондық 1000 санының екілік кодын алып көріңіз) ; екіншіден, тізбеленген бөлу операцияларының жүргізілу ұзақтығынан, қателік жіберу ықтималдығы да ұлғая түседі.
Айтылған тәсілдің кемістіктерінен құтылу мақсатында, автор ондық санның екілік кодын анықтауға іс жүзінде пайдаланып жүрген өз тәсілдерін ұсынады және оның біріншісін суреттеуге алдыңғы мысалда алынған 75 саны пайдаланылады:
- алдымен алынған ондық санның құрамына кіретін екінің ең жоғарғы дәрежесіндегі санның екілік коды жазылады (6410 = 26 = 12, бұл санды сөз ыңғайлылығы үшін бірінші қадам коды деп аталық) ;
-келесі қадамда түрлендірілетін саннан анықталған бірінші қадам коды алып тасталады да (75 - 64 = 11), қалған санның құрамына кіретін екінің ең жоғарғы дәрежесіндегі сан анықталады (810 = 23 = 10002, бұл санды екінші қадам коды деп аталық) ;
-осы тәртіппен жалғастыра отырып, ақырында өзімізге жатталымды кішігірім санның кодына жетеміз (11 - 8 = 3, 310 = 112) ;
-алынған бірнеше қадам кодтарын қосу арқылы қажетті код шығарылады.
Сонымен, қосу тәсілі деп аталатын бұл тәсілдің әр қадамында анықталатын кодтардың жазылымы да (1 және бірнеше нөл), олардың ақырында өзара қосылуы да оңай орындалатын операциялар болғандықтан бұл тәсіл арқылы ондық санның екілік кодын анықтау қиын болмайтындығы сөзсіз. Бірақ, кейбір жағдайда бұл тәсілді одан әрі жеңілдету мүмкіндігі туады. Мысалы, 1000 санының кодын шығару үшін алдыңғы тәсілді пайдалану алты қадамға созылады (512 + 256 + 128 + 64 + 32 + 8) . Алынған сан 512-ден гөрі 1024-ке (210) жуық, сондықтан бұл жерде қажетті кодты шығару үшін 1024 санының кодынан 24-тің кодын алу жеңіл болар еді деген ой туады. Бірақ, 1024-тің 1 түріндегі екілік кодынан 24 санының 11000 кодын алу тасымал арқылы жүзеге асырылатындықтан бұл оңай операция емес. 1024-тен 1 кемітілген 1023 санының коды болады және одан 23 санының 10111 кодын алу қиын емес.
2. 1 Негізгі функциялар
Цифрлық (логикалық) құрылғылардың кірістері мен шығыстарындағы кернеу мәндері логикалық 0 немесе логикалық 1 деп аталатын екі түрлі деңгейде болады. Логикалық құрылғылардың бұл ерекшелігі оларды жобалау үшін немесе осындай дайын құрылғылардың жұмысын талдау үшін логика алгебрасының (немесе Буль алгебрасының) қағидаларын пайдалануға мүмкіндік береді.
Цифрлық құрылғылардың атқарар қызметі сәйкесті логикалық функциялар арқылы сипатталады. Күрделілігі әртүрлі кез келген логикалық функцияны негізгі логикалық функциялар деп аталатын үш функция арқылы суреттеуге болады, олар - ЕМЕС, НЕМЕСЕ, ЖӘНЕ функциялары. Олардың атқарар қызметін кесте түрінде (ол ақиқаттық кестесі деп аталады) немесе сәйкесті логикалық өрнек арқылы суреттеуге болады.
ЕМЕС функциясы - аргументіне қарсы мәнді шығаратын, бір аргументті функция (1. 1-кесте), сондықтан бұл функция инверсия (inversion - терістеу) деп те аталады. Оның аргументі Х деп белгіленген болса, онда бұл функция Y= өрнегімен суреттеледі .
НЕМЕСЕ функциясы - аргументтерінің барлығы да 0 кезінде ғана 0 шығаратын, ал қалған жағдайда (яғни, аргументтерінің кем дегенде біреуінің мәні 1 болғанда) 1 шығаратын, бірнеше аргументті функция (1. 2-кесте) . Бұл функция дизъюнкция (disjunction) немесе логикалық қосу (logical addition) деп те атала береді. Оның логикалық өрнегі Х1Х0 түрінде суреттеледі.
ЖӘНЕ функциясы - аргументтерінің барлығы да 1 кезінде ғана 1 шығаратын, ал қалған жағдайда (яғни, аргументтерінің кем дегенде біреуінің мәні 0 болғанда) 0 шығаратын бірнеше аргументті функция (1. 3-кесте) . Бұл функция конъюнкция (conjunction) немесе логикалық көбейту (logical multiplication) деп те атала береді. Оның логикалық өрнегі Х1Х0 (немесе Х1Х0) түрінде суреттеледі.
ЕМЕС, НЕМЕСЕ, ЖӘНЕ функциялары арқылы кез келген күрделі функцияны суреттеуге болады, сондықтан, олар логикалық функциялардың түпнегіздік жинағын (core set) құрады.
2. 3 Әмбебап функциялар
Қарастырылған үш функциядан басқа, әмбебап функциялар деп аталатын екі функция бар, олар - НЕМЕСЕ-ЕМЕС және ЖӘНЕ-ЕМЕС функциялары. НЕМЕСЕ-ЕМЕС функциясы Пирс функциясы деп, ал ЖӘНЕ-ЕМЕС фукциясы Шеффер функциясы деп те атала береді. Олардың сәйкесті логикалық өрнектері және түрінде суреттеледі, ал атқарар қызметі 1. 4-кестеде келтірілген.
Цифрлық құрылғылардың схемаларын құру барысында оларды суреттеуші логикалық фунцияларды әртүрлі мақсатқа сай (мысалы, оларды қарапайым түрге келтіру үшін) түрлендіру қажет болады. Бұндай түрлендірімдер логика алгебрасының заңдары мен осы заңдардың жеке жағдайларға тікелей пайдалануға ыңғайландырып шығарылған заңдылықтарының негізінде жүргізіледі .
Бұл заңдар мен заңдылықтар - симметриялы, яғни олардың дизъюнкциялық және конъюнкциялық түрлері болады. Бұл заңдардың кейбірі дәстүрлі алгебрада қалыптасқан заңдар, сондықтан олардың дұрыстығы күмән тудырмайды, ал дәстүрлі алгебраға тән емес, жаңа заңдар мен заңдылықтардың дұрыстығына көз жеткізу (яғни, оларды дәлелдеу) аргументтерінің орындарына олардың сәйкесті мәндерін (0 мен 1) қойып тексеру арқылы жүзеге асырылады.
2. 4 Күрделі функциялар
Күрделі цифрлық құрылғылардың жұмысы әрине, қарапайым функцияларды нақтылы тәртіппен біріктіру арқылы көрсетілген күрделі функциялармен суреттеледі. Олар да қарапайым функциялар сияқты кесте түрінде немесе сәйкесті логикалық өрнек арқылы суреттеледі. Құрылғының жұмысын сипаттаушы логикалық өрнек арқылы оның схемасы құрылады. Демек, функция жазылымы күрделі болған сайын, оның схемасы да күрделі болады. Сондықтан, оларды мүмкіндігінше қарапайымдылау түрге келтіруге тырысу керек болады. Енді осы мәселелерді толығырақ қарастыруға кіріселік. Цифрлық құрылғының жұмысы көптеген жағдайда кесте түрінде беріледі. Әрине, оның мәтін түріндегі түсіндірме арқылы да берілуі мүмкін, бұндай жағдайда берілген түсіндірмені кесте түріндегі суреттемеге айналдыру керек болады. Сонымен, әңгімені кестеден басталық, ал құрылғы қызметінің түсіндірме арқылы берілу жағдайы кейінірек қарастырылады. Кесте түрінде сүреттелген функцияның (1. 1-кесте) логикалық өрнегін жазудың екі түрлі жолы (тәсілі) бар:
- көбейтінділердің қосылымы түрінде, яғни алдымен ЖӘНЕ функцияларын пайдаланып, сосын олардың нәтижесін НЕМЕСЕ функциясымен біріктіру арқылы жазу;
- қосындылардың көбейтілімі түрінде, яғни алдымен НЕМЕСЕ функцияларын пайдаланып, сосын олардың нәтижесін ЖӘНЕ функциясымен біріктіру арқылы жазу.
- кесте- сүреттелген функцияның логикалық өрнегін жазудың екі түрлі жолы
Бірінші тәсіл келесі тәртіппен жүзеге асырыла функцияның (Y) 1 мәнін қабылдайтын аргумент жинақтарының логикалық көбейтінділері жазылады;
-алдыңғы айтылған логикалық көбейтінділерді жазу кезінде 1 мәніндегі аргументтер тура түрінде алынады да, 0 мәніндегі аргументтер теріс түрінде алынады (бұндай жазылымдар конъюнктивті термдер деп аталады) ; жазылған конъюнктивті термдер логикалық қосу функциясы арқылы біріктіріледі.
Енді логикалық өрнектің жазылымының екінші тәсілін қарастыралық, ол келесі тәртіппен жүзеге асырылады:
функцияның 0 мәнін қабылдайтын аргумент жинақтарының логикалық қосындылары жазылады;
логикалық қосындыларды жазу кезінде 0 мәніндегі аргументтер тура түрінде алынады да, 1 мәніндегі аргументтер теріс түрінде алынады (бұндай жазылымдар диъюнктивті термдер деп аталады) ;
жазылған диъюнктивті термдер логикалық көбейту функциясы арқылы біріктіріледі.
Бұл тәсілмен логикалық функцияларды түрлендіру (минимизациялау) функция құрамындағы көрші термдерді тауып, оларға логика алгебрасының жоғарыда келтірілген заңдары мен заңдылықтарын тікелей пайдаланып біріктіру арқылы жүзеге асырылады. Көрші термдерге бір аргументінің ғана айырмашылығы бар термдер жатады.
2. 5 Логикалық функцияларды минимизизациялау
Алынған (1. 1) және (1. 2) өрнектерінің кез келгені арқылы берілген құрылғының схемасын құруға болады, бірақ бұл өрнектердің күрделілігіне байланысты құрылатын схема да күрделі болып шығады. Сондықтан, көптеген жағдайда схема құруға пайдаланылатын логикалық өрнекті қарапайым түрге келтіру (яғни, минимизациялау) керек болады. Минимизация жүргізудің бірнеше жолы бар, енді соларды қарастыралық. Карно картасы - логикалық өрнектерді минимизациялауға ыңғайлан-дырылған, функцияның кестелі суреттелімінің ерекше түрі. Жоғарыда алын-ған мысалдағы функцияға құрылған Карно картасы 1. 2-суретте келтірілген.
0
6
1
7
1
5
1
4
0
2
1
3
1
1
0
0
2. 1 сурет-Карно картасы
Карно картасында көрші термдер бірден көзге түседі: келтірілген картаның 1-, 3-, 5-, 7-ұяшықтарындағы бірліктердің өзара бірігіп, нәтижесінде одан X0 ғана қалатындығы және 4-ұяшықтағы бірліктің тек қана 5-ұяшықтағы бірлікпен бірігетіндігі көрініп тұр.
X1
2. 2 сурет-Төрт аргументті функцияға арналған Карно картасының түрі
Цифрлық құрылғыларды моделдеуге арналған бағдарламаларда мысалы, Electronics Workbench моделдеу жүйесінде минимизациялау жұмысын орындайтын арнайы түрлендіргіш (Logic Converter) орналастырылған осы аспаптың сыртқы түрі және ол арқылы алынған функцияның минимизациялануы келтірілген
3. 1 Дешифраторлар
Дешифратор (Decoder) - кірістеріне түскен екілік кодқа сәйкесті шығысында сигнал қалыптастырушы құрылғы. Мысал ретінде төрт теріс шығысты (Q3 … Q0) дешифратордың схемасын құру жолын қарастыралық. Шығыс саны төртеу болғандықтан, оның кірісіне түсетін код екіразрядты (A1A0) болады. Дешифратордың іске қосу кірісіндегі (E, Enable) сигналдың жандандыру деңгейін төменгі (0) мәнінде алалық.
2. 2К е с т е-Дешифратордың келтірілген түсіндірме суреттемесінің негізінде, оның ақиқаттық кестесі
Күрделі логикалық функцияның өрнегінің жазылу тәртібін қарастыру кезінде (1. 1. 4-тарау) функцияның алынған логикалық өрнегіне (1. 1) көз салсақ, ондағы әрбір термнің тура сегіз шығысты дешифратордың сәйкесті шығыстарының адресі екендігін көреміз. Демек, осындай дешифратордың сәйкесті шығыстарын бескірісті НЕМЕСЕ элементінің кірістеріне жалғау арқылы берілген функцияны жүзеге асыруға болады. Егер дешифратор теріс шығысты болса, онда (1. 1) өрнегін де Морган заңы арқылы түрлендіремАлынған өрнектен берілген құрылғының қызметін теріс шығысты дешифратор негізінде жүзеге асыру үшін оның сәйкесті шығыстарына бескірісті ЖӘНЕ-ЕМЕС элементін жалғау жеткілікті екендігі көрініп тұр Қиыстырма құрылғыны дешифратор негізінде құру тәсілі - аса ыңғайлы тәсіл: біріншіден, логикалық өрнекті минимизациялаудың қажеті жоқ (дәлірек айтқанда, өрнектің де қажеті жоқ, қажетті жалғамдар кестеден көрініп тұр), екіншіден, жалғыз дешифратор негізінде бірнеше функцияны қатар жүзеге асыруға болады.
3. 2 Логикалық элементтер
Логикалық элементтер - логикалық функцияларды жүзеге асыруға арналған құрылғылар. 1. 4-суретте бұрын қарастырылған қарапайым функцияларды жүзеге асырушы сәйкесті логикалық элементтердің шартты сызба белгілемелері келтірілген. Бұнда шығыс сигналының өзгерісінің кіріс сигналының өзгерісінен нақтылы уақытқа кідіретіндігі айқын көрініп тұр. Біздің Electronics Workbench моделдеу жүйесінде жүргізген өлшеміміз бойынша ондағы ЕМЕС элементіндегі сигнал кідірісі 10 ns шамасында болады. Әрине, статикалық (яғни, белгілі уақыт аралығында тиянақты мәнін сақтайтын) сигналдармен істейтін құрылғылардың жұмысына бұндай кідірістің байқарлықтай әсері болмайды. Бірақ кейбір жағдайларда (мысалы, тізбектеме құрылғыларда) бұндай кідірістің құрылғының жұмысына байқарлықтай әсер етуі мүмкін. Кідіріс әрекетін суреттеу мақсатында екі ЕМЕС элементінің кірістеріне қатар берілген екі сигналдың осы элементтер арқылы алынған логикалық қосындысын қарастыралық (1. 6-сурет) . Схемада көрсетілгендей, бір сигнал екінші элементтің кірісіне екі ЕМЕС элементі арқылы берілген. Сезімтал осциллограф арқылы алынған диаграммада (1. 7, b-сурет) екінші элементтің бір кірісіне сигналдың екі ЕМЕС элементінен өтуге кеткен 20 ns кідірісінің әсерінен осы элементтің шығысындағы сигнал құрамына бөгде теріс импульстің қосылғанын көреміз. Сигнал құрамындағы бұндай бөгде импульс осы сигналдың түсетін құрылғысының бағдарланған жұмысын бүлдіруі мүмкін, сондықтан бұндай жағдайдың болмауын қамтамасыз ету керек.
ЕМЕС функциясы - аргументіне қарсы мәнді шығаратын, бір аргументті функция (1. 1-кесте), сондықтан бұл функция инверсия (inversion - терістеу) деп те аталады. Оның аргументі Х деп белгіленген болса, онда бұл функция Y=өрнегімен суреттеледі.
2. 3 кесте-функция өрнегі
НЕМЕСЕ функциясы - аргументтерінің барлығы да 0 кезінде ғана 0 шығаратын, ал қалған жағдайда (яғни, аргументтерінің кем дегенде біреуінің мәні 1 болғанда) 1 шығаратын, бірнеше аргументті функция (1. 4-кесте) . Бұл функция дизъюнкция (disjunction) немесе логикалық қосу (logical addition) деп те атала береді. Оның логикалық өрнегі Х1Х0 түрінде суреттеледі.
2. 4 кесте -1 шығаратын, бірнеше аргументті функция
ЖӘНЕ функциясы - аргументтерінің барлығы да 1 кезінде ғана 1 шығаратын, ал қалған жағдайда (яғни, аргументтерінің кем дегенде біреуінің мәні 0 болғанда) 0 шығаратын бірнеше аргументті функция (1. 5-кесте) . Бұл функция конъюнкция (conjunction) немесе логикалық көбейту (logical multiplication) деп те атала береді. Оның логикалық өрнегі Х1Х0 (немесе Х1Х0) түрінде суреттеледі.
2. 5 кесте- 0 шығаратын бірнеше аргументті функция
3. 3 Қиыстырма құрылғыларды құру тәртібі
Қиыстырма құрылғыларды құру келесі тәртіппен жүргізілед құрылғының сөз-сөйлем түріндегі түсіндірмесінің негізінде оның ақиқаттық кестесі құрылады құрылған кестедегі деректер негізінде құрылғының жұмысын суреттеуші логикалық өрнек жазылады қажетті жағдайда алынған логикалық өрнек минимизацияланады алынған өрнек құрылғыны құруға бағдарланған түпнегіздік жинаққа (core set) сай түрлендіріледі ақырғы алынған өрнек негізінде түпнегіздік жинақтың элементтері арқылы құрылғының схемасы құрылады. Құрылғыны құру тәртібінің бастапқы үш кезеңі бұрын (1. 1. 4-тарауда) қарастырылған болатын, сондықтан сонда алынған өрнек негізінде негізгі элементтер жинағының элементтері (ЕМЕС, НЕМЕСЕ, ЖӘНЕ) арқылы құрылғының схемасын құрамыз
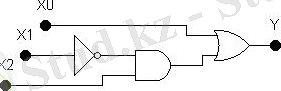
2. 2сурет -Негізгі элементтер жинағының элементтері (ЕМЕС, НЕМЕСЕ, ЖӘНЕ) арқылы құрылғының схемасы
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz