Зертханалық жұмыс № 4.5: дифракциялық тордың тұрақтысын анықтау


№ 4. 5 зертханалық жұмыс
ДИФРАКЦИЯЛЫҚ TOP ТҰРАҚТЫСЫН АНЫҚТАУ
Алматы, 2022

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
АБАЙ АТЫНДАҒЫ ҚАЗАҚ ҰЛТТЫҚ ПЕДАГОГИКАЛЫҚ УНИВЕРСИТЕТІ
Бекітемін
Физика кафедрасының меңгерушісі Косов В. Н.
«» 2022 ж.
№ 4. 5 зертханалық жұмыс
ДИФРАКЦИЯЛЫҚ TOP ТҰРАҚТЫСЫН АНЫҚТАУ
Жұмыстың мақсаты: Дифракциялық тордағы Фраунгофер дифракциясын оқып уйрену. Мөлдір дифракциялық тордың тұрақтысын анықтау.
Қажетті құрал-жабдықтар: мөлдір дифракциялық тор, гелий-неон лазері, оптикалық отырғыш, рейтер, шкаласы бар экран, толқын ұзындығы белгісіз лазер.
Қысқаша теориялық кіріспе
Жазық мөлдір дифракциялық тор орталарының ара қашықтығы
және ені бірдей
, саны өте үлкен (1 мм де 1000 дейін) жіңішке параллель саңылаулардан тұратын мөлдір пластинка түрінде болады. Тордың саңылауы дұрыс құрылымды болады. Мұндай құрылымдағы тордың саңылауы мен оның аралықтарынан жарық өткізу коэффициенті әртүрлі болатындықтан, мөлдір амплитудалық тор деп атайды.
- қашықтығы тор тұрақтысы немесе периоды деп аталынады.
1-суретте Фраунгофер схемасына сәйкес торлар арқылы өтетін сәулелер жолы көрсетілген. Жарық көзінен (1) монохроматты жарық саңылауды (2) жарықтандырады, ол (3) коллиматордың объективінің фокаль жазықтығында орналасады. Саңылаудың (2) әр нүктесі екінші жарық көзі болғандықтан, объективтен (3) өткен соң параллель сәулелер береді. Қорытынды сәуле дифракциялық торға параллель сәулелер шоғы түрінде жетеді. Бүл сәулелер тордан өтерде дифракцияланып, когерентті бұрышынан шашырайтын жарық шоғын түзеді. Көру трубасының объективінен өтетін шоқтар оның фокаль жазықтығында саңылаудың кескіні болатын дифракциялық бейне түзеді. Бұл жазықтықтағы (6) жазықтықтағы когерентті тербелістердің интерференциясының нәтижесі болады.
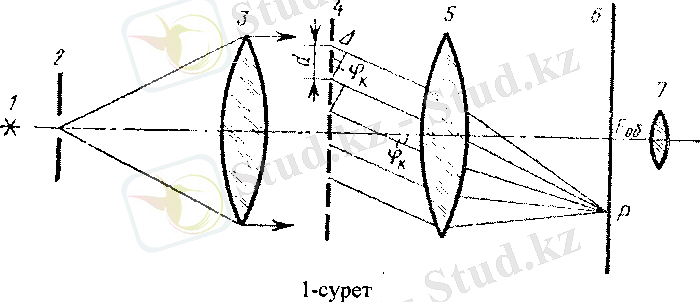
Сурет 1 - Фраунгофер схемасына сәйкес торлар арқылы өтетін сәулелер схемасы
Дифракциялық бейнедегі интенсивтіліктердің таралуы әр саңылаудагы интенсивтіліктің таралуы мен барлық саңылаудан болатын толқынның интерференциясын ескергенде алынады. Әр саңылау 2-суретте келтірілген дифракциялық бейне береді. Бұл жағдайда бірінші болатын минимумдар шарты былайша беріледі:
b sin ±m , m= 1, 2, 3, . . . (1)
- дифракция бұрышы m = 0 болғанда максимум болады, λ - жарық толқынының ұзындығы. Максимумдар шарты:
bsin = bsin (1а)
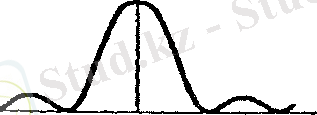
-2 0 2
Сурет 2 - Саңылаудан шыққан дифракциялық бейне
Барлық саңылаудан бейне жазықтықтың бір нүктесіне келіп, бірін-бірі күшейтеді. Әр саңылауда тербелістер когерентті болатындықтан, қорытынды интенсивтілікті табу үшін олардың қабаттасқандағы фазалық қатынастарын табу керек. Ол үшін алынатын толқынды беттің бөлігін саңылауларға параллель тар зоналарға бөлеміз. і - зонаның Р нүктесіндегі тербеліс амплитудасьшың векторын былай белгілеуге болады:
 ,
,
мұндағы
 і - саңылаудың Р нүктесіндегі тербеліс амплитудасы (2-сурет) .
і - саңылаудың Р нүктесіндегі тербеліс амплитудасы (2-сурет) .
Бұл векторлардың модулдары бірдей және дифракция бұрышына байланысты болады. Келесі әр вектор алдыңғысына қарағанда бір бұрышқа бұрылған, ол көршілес саңылаулар қоздырған тербелістердің фаза айырымына тең (3а-сурет) .
(1) -шартты қанағаттандыратын бағыттар үшін, барлық
 тең және қорытқы тербелістер (6) - жазықтықтың Р нүктесінде нольге тең болады. Сонымен бір саңылау үшін минимум шарты, тор үшін де минимум шарты болалады. 1-суреттен көрініп тұр, көршілес саңылаулардың жол айырымы
тең және қорытқы тербелістер (6) - жазықтықтың Р нүктесінде нольге тең болады. Сонымен бір саңылау үшін минимум шарты, тор үшін де минимум шарты болалады. 1-суреттен көрініп тұр, көршілес саңылаулардың жол айырымы
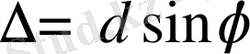 -ға тең болатындығы. Сондықтан фазалар айырымы тең болады:
-ға тең болатындығы. Сондықтан фазалар айырымы тең болады:
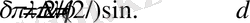
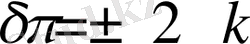 болатын барлық бағыттар үшін, интенсивтіліктің максимумдары пайда болады. Сондықтан, бас максимумның шарты:
болатын барлық бағыттар үшін, интенсивтіліктің максимумдары пайда болады. Сондықтан, бас максимумның шарты:
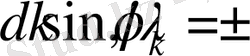 (2)
(2)
бұл жерде k = 0, 1, 2, … - дифракциялық максимумның реті.
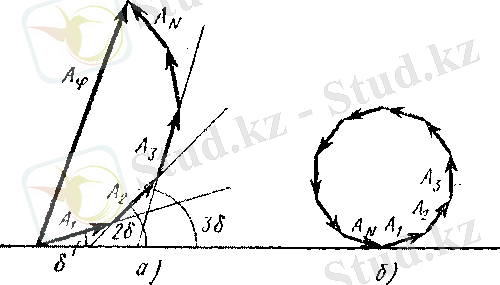
3-сурет. Графикалық әдіспен қорытқы амплитуданы анықтау
Фокаль жазықтығының сәйкес нүктелеріндегі тербеліс амплитудасы:
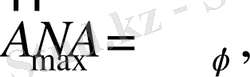
мұндағы
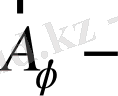 бір саңылаудан
бір саңылаудан
 бұрыш бағыты бойынша дифракцияланатын тербелістің амплитудасы;
N -
тордағы саңылау саны;
бұрыш бағыты бойынша дифракцияланатын тербелістің амплитудасы;
N -
тордағы саңылау саны;
Сонымен, бас максимумдардың интенсивтілігі I мах тор саңылауларының санының квадратына пропорционал болады:
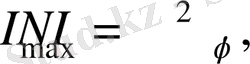
мұндағы
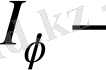 бір саңылаудың
бір саңылаудың
 бағытындағы интенсивтілігі (4-сурет) .
бағытындағы интенсивтілігі (4-сурет) .
4-сурет
Жеке саңылаулардың тербелістері бірін-бірі өшіретін бағыттар үшін минимум шартын аламыз: (3б-сурет)
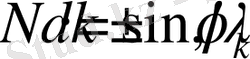
немесе
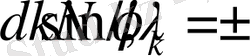
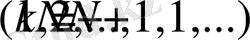 .
.
Интенсивтіліктің қорытқы таралуы 4-суретте көрсетілген. Пунктирлі қисық бір саңылаудың
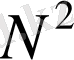 -қа көбейтілген интенсивтілігін береді. Тұтас қисық бас максимумге, сол сияқты қосымша максимум мен минимумға сәйкес келеді.
-қа көбейтілген интенсивтілігін береді. Тұтас қисық бас максимумге, сол сияқты қосымша максимум мен минимумға сәйкес келеді.
Егер жарық көзі монохроматты емес жарық шығарса, онда тор оны спектрге жіктейді. k = 0 болғанда барлық толқын үшін сәйкес келетін нольдік ретті максимум пайда болады. Оның екі жағынан ± k ретті спектр-максимумдар пайда болады. Әр максимум ретінде қысқа толқындар максимумы нольдік ретке жақын орналасады. Ұзын толқындар одан алысырақ орналасады.
Дифракциялық тордың жарықты спектрге жіктеуі оны дисперсиялық қондырғы ретінде спектральдық құралдарда пайдалануға мүмкіндік береді. Дифракциялық тордың негізгі сипаттамасы - бұрыштық дисперсиясы мен ажырату қабілеті .
Бұрыштық дисперсия былай өрнектелінеді:
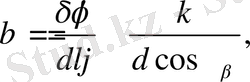 (3)
(3)
мұндағы
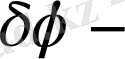 екі спектральды сызық аралығындағы бұрыштық қашықтық,
екі спектральды сызық аралығындағы бұрыштық қашықтық,
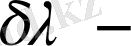 осы аралықтағы толқындар айырымы,
k -
спектр реті,
осы аралықтағы толқындар айырымы,
k -
спектр реті,
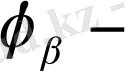 дифракция бұрышы.
дифракция бұрышы.
(3) формуланы (2) өрнекті дифференциалдау арқылы алуға болады. Сонымен бұрыштық дисперсия спектр ұзындығын немесе тордың әр түрлі ұзындықтағы жарық шоқтарын кеңістікте бөлу қабілетін сипаттайды.
Ажырату қабілеті R мынандай формуламен есептелінеді:
(4)
мұндағы - ең жақын ажыратылатын екі спектралды сызықтардың толқын ұзындықтарының айырымы ( және ), к - спектр реті, N - тордағы штрихтар саны (5-сурет) .
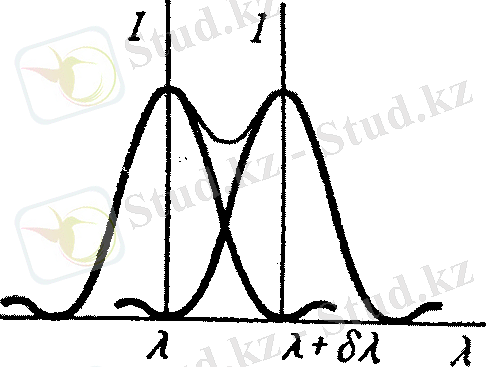
5-сурет. Рэлей шарты бойынша, екі көршілес орналасқан максимумдардың ажыратылуы көрсетілген
(4) -қатынаспен анықталатын ажырату қабілеті Рэлей критерийіне сәйкес келеді. Рэлей шарты бойынша, егер біреуінің максимумы (ортасы) көршісінің минимумына (шетіне) сәйкес келсе, онда олар ажыратылған деп есептелінеді.
5-суретте ажыратылған екі спектральды сызық графикте көрсетілген. Бұдан жақын орналасқан сызықтар Рэлей критерийі бойынша ажыратылмаған болады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz