Жіңішке саңылаудан өткен лазер жарығының дифракциялық кескініндегі интенсивтіліктің таралуын зерттеу

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

АБАЙ АТЫНДАҒЫ ҚАЗАҚ ҰЛТТЫҚ ПЕДАГОГИКАЛЫҚ УНИВЕРСИТЕТІ

Бекітемін

Физика кафедрасының меңгерушісі Косов В. Н.

«» 2022 ж.

№ 4. 6 зертханалық жұмыс

БІР ЖӘНЕ ЕКІ САҢЫЛАУДАН ӨТКЕН ЖАРЫҚТЫҢ ДИФРАКЦИЯСЫН ОҚЫП-ҮЙРЕНУ

Алматы, 2022

№ 4. 6 зертханалық жұмыс

БІР ЖӘНЕ ЕКІ САҢЫЛАУДАН ӨТКЕН ЖАРЫҚТЫҢ ДИФРАКЦИЯСЫН ОҚЫП-ҮЙРЕНУ

Жұмыстың мақсаты: Жіңішке саңылаудан өткен лазер жарығының дифракциялық кескініндегі интенсивтіліктің таралуын зерттеу.

Құралдар мен жабдықтар: Жарық көзі - (He-Ne) лазері, спектралдық саңылау түріндегі жылжымалы саңылау, мөлдір емес шыны экран, фототіркегіш - микроамперметр мен электрондық күшейткіші бар фотодиод.

Қысқаша теориялық кіріспе

Фраунгофер дифракциясы коллиматорлар арқылы алынған параллель сәулелерде байқалады. Лазерлерді қолданғанда оптикалық жүйе көп қарапайымдалады, өйткені лазер шығаратын когерентті жарық шоқтары параллель болып, коллинациялау үшін ешқандай оптикалық жүйені кажет етпейді. Бір саңылауда бақыланатын Фраунгофер дифракциясының схемасы 1-суретте келтірілген.

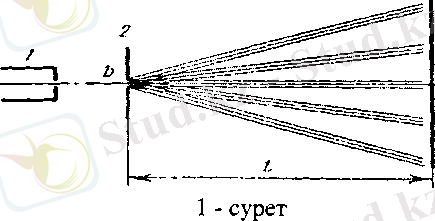
Сурет 1 - Бір саңылауда бақыланатын Фраунгофер дифракциясының схемасы

(He - Ne) - лазерінен шыққан параллель жарық сәулесі (1) саңылауға (2) нормаль түседі. Саңылау ұзындығы енінен әлдеқайда артық болады. Гюйгенс принципі бойынша жарық келіп жеткен саңылау жазықтығының әр нүктесі екінші ретті толқындар көзі болып табылады. Олар φ1, φ2, φ3 . . . бұрыштарымен диффракцияланып жан-жаққа тарайды, саңылаудан өткен жарық дифракцияланады. Дифракцияланған сәулелер когерентті болғандықтан, қабаттасканда интерференциялануы мүмкін. Интерференция нәтижесі ннтенсивтіліктің 3 экрандағы периодты таралу түрінде бақыланады. Экран 2 саңылаудан

\[l\Delta~~~^{2}/\lambda\]

қашықтықта орналасады.

Гюйгенс-Френель принципі бойынша экранның белгілі бір нүктедегі интенсивтіліктің таралуынан, саңылаудың әр элементінен келетін элементар толқындардың амплитудасы мен фазасын ескеріп қосу арқылы анықтауға болады.

Аз дифракциалану бұрышында интенсивтілікті Френель ұсынған графиктік әдіс бойынша есептеуге болады. Ол үшін саңылаудағы толқын фронтының ашық бөлігін саңылау шетіне параллель екі бірдей зоналарға - жіңішке жолақтарға бөлеміз. Бұл жағдайда саңылау жазықгығындағы толқын толқындық бетке сәйкес келеді, яғни оның барлық нүктесіңдегі фазалары бірдей болады. Әр зона (жолақ) элементар екінші ретті толқын көзі болып табылады. Әр зонадағы тербелістің амплитудасы бірдей ∆ А және алдыңғы тербелістен бірдей фаза δ -ға қалып отырады. δ шамасы бақылау нүктесінің Р бағытын анықтайтын дифракциялану бұрышына тәуелді болады. Φ = 0 фазалар айырымы δ = 0 болып, векторлық диаграммасы 2а-суретте көрсетілгендей болады.

Қорытынды тербеліс амплитудасы А ₀ қосылатын тербелістердің амплитудаларының алгебралық қосындысына тең болады. Егер қосылатын тербелістердің саңылау шетіндегі фазалар айырымы π болса (жол айырымы ∆=bsinφ=λ/2), онда ∆Α векторлары ұзындығы А ₀ жартылай шеңбердің диаметрі бойымен орналасады. Сол себепті қорытынды амплитуда шамасы А = 2A ₀ / π болады. ∆= asinϕ = λ жағдайында саңылау шеттеріндегі фазалар айырымы 2π-ге ажыратылады.

Сәйкес векторлық диаграмма 2-суретте келтірілген. ∆Α векторлары ұзындығы Α ₀ шеңбер бойымен орналасады. Қорытынды амплитуда нөлге тең, ол бірінші минимумға сәйкес келеді.

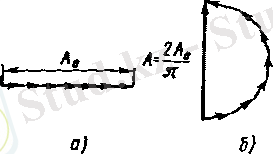
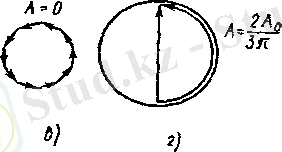
Сурет 2 - Векторлық диаграмма

Бірінші максимум ∆ = b sinφ = 3λ / 2 жағдайында бақыланады. Бұл жағдайда саңылау шетіндегі фазалар айырымы 3π -ге тең. ∆ А векторларын тізбектеп құру арқылы біз диаметрі ∆ А = 2Α ₀ / 3π шеңберін бір жарым есе айналып шығады. Сонымен А ₁ бірінші максимум амплитудасы нөлінші максимум А ₀ амплитудасының 2 / 3π бөлігін құрайды, ал интенсивтіліг I ₁ ∼ $A_{1}^{2}$ = $\left. ⟦\frac{2}{3\pi} \right. ⟧$ · $A_{0}^{2}$ ≈ 0, 045 ·Ι ₀ . Осындай жолмен басқа максимумдардың да салыстырмалы интенсивтілігін табуға болады.

Нәтижесінде интенсивтіліктердің мынадай қатынасы туындайды:

I ₀ : I ₁ :…. . I _n = 1: (2 /3π) ² : ……. = 1: 0, 045: ….

Графикалық есептеу жуықты болғандықтан, алынған нәтиже де жуықты болып есептеледі.

Сонымен ортаңғы нөлдік максимум басқа максимумдардың интенсивтілігінен әлдеқайда басым болады. Оған саңылаудан шыққан жарық ағынының 90% сәйкес келеді.

Нөлдік амплитуданың мынадай дифракциялану бұрышына $\varphi_{к}$ сәйкес келетінін байқау қиын емес:

bsin $\varphi_{к}$ = I· k· λ,

мұндағы k=1, 2, 3 . . . - дифракциялық минимум реті. k=0 болғанда, $\varphi_{0}$ =0, bsin $\varphi_{к}$ =0 шартына сәйкес келеді, бұл нөлдік ретті орталық максимум шартына сәйкес келеді.

Дифракциялық максимум шарты нақтыланған формула арқылы өрнектеледі:

bsin $\varphi_{к}$ = $\pm 1, 43$ λ, bsin $\varphi_{к}$ = $\pm 2, 46$ λ, bsin $\varphi_{к}$ = $\pm 3, 47$ λ.

Интенсивтіліктердің экранда (3) таралуы 3-суретте келтірілген. Фраунгофер дифракциялық кескінінің бақыланушылығы саңылау еніне және саңылаудан экранға (3) дейінгі қашықтығына байланысты болады.

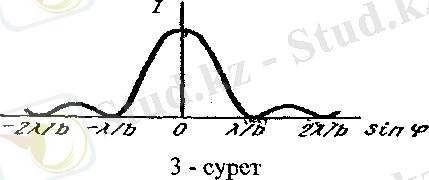
Егер саңылау ені b = λ болса, онда sinφ ₁ =1, φ ₁ = π /2 болып, ешқандай минимум бақыланбай, экран толығымен жарықталынады, ортасында басымдау, шетінде бәсеңірек болады. Бұл интерференциясыз таза дифракция жағдайына сәйкес келеді. Аз дифракциялану бұрышында өте кішкене кескінді бақылау қиынға соғады.

Бұл жұмыста дифракциялық кескін айқын бақыланатын жэне интенсивтіліктің таралуының экспериментальдық графигін тұрғызуға болатын саңылаудағы дифракцияның схемасын кұру ұсынылады.

Қондырғының сипаттамасы

Қондырғы 4-суреттегі схема бойынша жинақталады. Кванттық генератор 1, оптикалық скамьяға қалған бөлігі бос болатындай етіп орналасады. Скамьяның бос бөлігіне екі рейтер орналасады, біреуі бекіткіші бар саңылаудан 2, ал екіншісі мөлдір емес экран 3 пен фотодиод 4 кезек-кезек орналасу үшіін ауыспалы бекіткіштен тұрады. Саңылау бекіткішінің көлденең бағытта аздап қозғалта алатын қондырғысы болуы керек. Фотодиод бекіткіші оны ортаңғы күйінен 100 мм аралықта көлденең бағытта жылжытатын бағыттаушылары болуы керек. Фотодиодтың орын ауыстыруы тіркеу үшін бекіткішке құны 1 мм сызғыш бекітіледі. Рейтердің және лазердің орнын есептеу үшін скамья ұзындығы 1 м құны 1 мм сызғышпен жабдықталуы керек. Жұмысқа кванттық генератор мен оның қолданылуының нұсқауы қосылады.

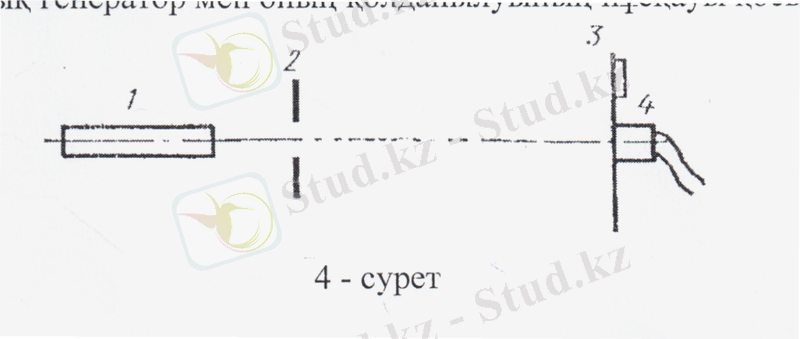
10001

4-сурет. Кондырғы схемасы

Тапсырма: Саңылаудағы дифракциялық кескіннің интенсивтілігінің таралуын зерттеу.

4-сурет бойынша 2-рейтерге бекіткіші бар саңылау, ал 3-рейтерге мөлдір емес экран орналасады. 2-рейтер лазерден кем дегенде 200 мм аралықта болуы керек, ал 3-рейтер оптикалық скамьяның шетінде орналасады.
Лазерді қосыңыз.
Саңылау енін озгерту арқылы экранда дифракциялық кескін алыңыз. Минимумдардьщ аралығы кем дегенде 10 мм болу керек. Кескіннің айқын жағдайын алыңыз. Ол үшін саңылауды көлденең бағытта жылжыту арқылы лазер сәулесінің шоғы саңылауды симметриялы жабатындай етіп орналастыру қажет. Саңылау жазықтығының көлбеулігін өзгерту арқылы шоқтың перпендикуляр түсу жағдайына келтіріңіз. Шағылған сәулелер кері бағытта, лазердің шығатын терезесіне бағытталуы керек.
Экранды алып, дифракциялық кескін деңгейінде фотодиодты орналастырыңыз.
Фотодиодты қосыңыз. Фотодиодтың жарық қабылдағыш терезесін жауып, фотодиодтың қараңғылық тогын-ді өлшеңіз.
Фотодиодты ашыңыз. Фотодиодты дифракциялық кескін бойымен жылжытып, тура және кері бағыттағы токтыңшамасын жазып алыңыз. Қажетті жағдайда микроамперметрдің сезгіштігін өзгертуге болады. Ең аз шама микроамперметр шкаласының кем дегенде бес бөлігіне сәйкес келуі қажет.
Қараңғылық токты ескеріпдифракциялық кескіндегі интенсивтілік реттелуінің фототока пропорционалдігінің графигін сызыңыз. Микроамперметр сезімталдығының өзгеруін ескеру қажет.
Қарастырған координатада, максимум шамасын жуықтап алғанда төмендегідей болады деп, интенсивтілік реттелуінің теориялық графигін сызыңыз (3 сурет) .

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.