Физикалық есептер шығару үрдісінің кезеңдері

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 59 бет
Таңдаулыға:

Күрделі есептер шығару әдістемесі пәнінен
ДӘРІСТЕР ТЕЗИСІ

ДӘРІС №1. Есептер шығарудың маңызы, олардың оқу үрдісіндегі орны. Есептің күрделілігі мен қиындығы. Физикалық есеп ерекшеліктері. Физикалық есеп шығару үрдісінің мәні.Физикалық есеп шығару үрдісінің психологиялық ерекшеліктері.

Физика пәнінен есеп шығару - оқу үрдісінен бөліп алуға болмайтын бір бөлігі болып табылады, себебі ол физикалық ұғымдарды қалыптастыруға, оқушылардың физикалық құбылыстарды оқып үйренуіне, ойлау қабілетін дамытуға, білімдерін нақтылауға, оны практикада қолдана білуге үйретуде маңызы зор.
Есептер шығару физикалық заңдарды оқып үйренуде, тереңірек және нақты білім алуға, алған білімдерін берік меңгеруге, логикалық ойлау қабілетінің дамуына, белсенді болуына, физика пәніне деген қызығушылығын арттыруға, алға қойған мақсатқа жетуде табандылыққа, өзіндік жұмыс істеу, өз бетімен білім алу дағдысына ие болуға көмектеседі. Есептер шығаруды мына жағдайларда қолданады:
а) проблемалық ситуация туғызуда;
ә) жаңа мәлімет беруде;
б) практикалық іскерлік пен дағдыларды қалыптастыруда;
в) білімін (нақтылығын және тереңдігін) тексеруге;
г) бекітуге, материалды қайталауға;
д) техникалық құрылғылардың жұмыс істеу принциптерін түсіндіруде;
е) оқушылардың шығармашылық ойлау қабілетін жетілдіруде.
Физика есептерінің оқу үрдісін ұйымдастыруда алатын орны ерекше. Оқушыларға есептерді шығартып үйретудің мынандай тәсілдерін беруге болады.
1) Мұғалім есепті оқып, талдау жасап, әр түрлі сұрақтар беру арқылы сыныпты есеп шығаруға жұмылдыра отырып, тақтаға есепті өзі жазып, берілгенін жазып көрсетеді. Мұндай тәсіл жаңа сабақты түсіндіріп болғаннан кейін қолданылады. Мұғалім орташа қиындықтағы есепті таңдап алғаны дұрыс.
2) Есепке талдау жасап талқылау мұғалімнің басшылығымен бүкіл сынып болып талқыланып, одан кейін бір оқушыны тақтаға шығарып, қалғандары орындарында шығару. Мұнда тақтаға орташа оқитын оқушыны шығарған дұрыс. Себебі жақсы оқитын оқушы есепті тез шығарады да, қалғандары оған ілесе алмайды, ал нашары тіптен шығара алмайды.
3) Мұғалім қандай есепті шығару керектігін айтады, оқушылар оны өзінше орындайды. Мұнда мұғалімнің әр есептің түріне қарай кететін қателерге кеңес беріп отырғаны жөн. Мұнда оқушыларға әр деңгейдегі есеп карточкаларын жасап, өздік жұмысты сол арқылы орындаса да болады.
Бұл үш тәсілден басқа есепті шығаруды сыныптан тыс уақытта физикаға қызығатын оқушылардың есеп шығару үйірмесін ұйымдастыру арқылы шығаруға болады.

Есептің күрделілігі мен қиындығы. Кез келген есептің күрделілігі оның құрылымымен
1) нысандар саны, сипаты және олардың берілу түрімен;
2) есеп шартында және талабында келтірілген нысандар айқындығымен және нысандар сипаттарының логикалық , функциональдық қатыстарымен анықталады.
Есеп күрделілігі шығарушы субъектінің әрекетіне тәуелді болмайтын оның нақты (объективті) сипаты болып табылады.
Физикалық есептің күрделілігі оның құрастырушысымен беріледіжәне көптеген себептерге байланысты болады. Оларға, ең алдымен, есеп құрастырудың дидактикалық мақсаты мен оқушылардың межеленген дайындық деңгейін жатқызуға болады.
Тек қана есепті талдау немесе шығару барысында, тұлға күрделі есепті қиын есеп деп сезінеді (күрделі есеп қиын есепке түрленеді).
Бастапқы кезде, тұлға қиын деп сезінетін есеп, оның күрделілігімен ( құрылымы бойынша) анықталады да, оқушының есеп шарты мен талабын түсіну деңгейіне және қарастыратын жағдадың мәні болатын, проблемді анықтай білу ебдейлігіне тәуелді болады.
Есепті талдай отырып, әрбір оқушы оның қиын екендігін тек өзі үшін ғана тағайындайды, себебі бір адам үшін қиын болған есеп, екінші адам үшін оңай болуы мүмкін. Яғни, есептің қиындығы - оның күрделілігі ғана емес, тұлғаның есепті шығару дағдылары мен ебдейліктеріне де байланысты болатын - субъективті сипаттама.
Физикалық есеп ерекшеліктері. Есептер әр түрлі белгілері бойынша жүйеленеді, бірақ ол жүйелердің өзіне сай ерекшеліктері болады, олар физика сабағында ескерілуі қажет. Физикалық есептердің ерекшеліктеріне мыналарды жатқызуға болады;
1. Физика есептерін шығару үшін, есеп шартын талдағанда "идеалдауды" жиі қолданады.
1. Көп жағдайда есепті шығару үшін, есепті талаптары әр түрлі болатын екі, үш идеал есепке бөледі.
2. Есепті дұрыс шығару үшін, қарастырылатын құбылыстарды түсіндіретін физикалық заңдарды анықтау керек.
3. Есеп шарттары график, кесте, кескін түрлерінде де беріледі. Шаманың бірде нақты сандық мәні ізделсе, кейде құбылыстардың заңдылықтарын түсіндіру қажет болады.
R
R
2R
3R
τ, с
t, 0C
Мысалы: 1 - сурет

4. Физикалық есептердің өзіндік, ерекше түріне тәжірибелік есептер жатады. Мысалы, сызғыш және микрометр көмегімен мыс сымның кедергісін R=ριs формуласын қолданып анықтау.
5. Физикалық есептердің ең маңызды ерекшелігі - физикалық шамалардың өлшемі болады. Өлшемдерді талдау физикалық есептер шығарудың мықты аппараты болып табылады.
6. Есепте кездесетін физикалық нысандардың сипаттарының көпшілігі - векторлар. Сондықтан есеп шартын талдағанда физикалық шамалардың скаляр немесе вектор екенін анықтайды, себебі қолданылатын математикалық аппарат осымен анықталады.
Физикалық есеп шығару үрдісінің мӘні.
Физикалық есеп шығару дегеніміз не? - деген сұрақ жауабы есеп шығару үрдісінің мәнін анықтайды.
Физикалық есеп шығару үрдісі күрделі ой әрекетіне жатады. Сондықтан оның психологиялық ерекшелігі бар. Екіншіден бұл үрдіс оқу-танымдық мақсатта жүргізіледі, сондықтан оның дидактикалық ерекшеліктері болады.
Физикалық есеп шығару үрдісінің психологиялық ерекшеліктері.
Физикалық есептерді шығарудың негізгі психологиялық механизмдеріне мақсаттану (мотив), ұстаным (установка), бағдарланулар жатады.
Мақсаттану - субъектің не себепті есеп шығаратыны - қажеттіктерінен туындап, оның есеп шығару қарекетінің белсенділік деңгейін анықтайды мақсаттану күшейген сайын, оқушының есеп шығармақ ішкі қажеттігі артып, көңіл-күйі көтеріледі, ал есеп шығарудағы жетістік мықты қанағаттану сезімін туғызады.
Ұстаным - есеп шығару үрдісін жүзеге асыру барысындағы - тұлғаның ахуалы. Ол тұлғаның есеп шығару әрекетіне дайындығын анықтайды.
Ұстаным қандайда бір қажеттіктерден туындайтын мақсаттануды күшейте де, әлсірете де алады. Мақсаттану өзгере алады. Ұстаным одан гөрі орнықтырақ, кейде мақсаттанудың болу-болмауына көрініс береді.
Физикалық, есеп шығару кезіндегі тұлғаның бағдарлануы - жаңа есеп қарастырғанда туындап, өзі үшін проблемдік болатын ахуалды дұрыс бағалау және пайда болған мәселені шешуге бағытталған әрекет тәсілдері туралы белгілі бір шешімді жүзеге асыру мүмкіндіктері.
Есеп шығару барысындағы бағдарлану - тұлғаның біліміне, дағдыларына және ебдейліктеріне, оның өз қарекетін ұйымдастыру қабілеттеріне негізделген ізденім әрекетінің ерекше сүлесі (типі).
Бағдарлану кезінде есеп талданады, нысандардың сипаттары мен параметрлері зерттеледі, ізделінді шамалар анықталып, олардың жеке белгілері салыстырылады. Кәдуілгі жағдайда тұлға өз жадынан шығарылмақ есепке ұқсас есептерді іздеп, оны бұрын шығарылған есепппен байланыстыруға әрекет жасайды.
Терең мақсаттанған ізденіс кезінде, тұлға - есеп шығарудың, өзіне белгілі, барлық әдіс, тәсіл, амалдарын теріп шығады.
Бағдарлану әрекеті кезінде тұлға ойында есеп шығару мүмкіндіктері жайлы болжам (гипотеза) - есеп шығарудың жалпы жоспары туындайды, оның бөліктері болжамды тексеру үрдісі кезінде нақтыланады. Нәтижеде есеп шығару жоспары айқындалып, жаңа бөліктермен толықтырылады, ізденім әрекетінің келер сатылары нақтыланады.
Егер есеп шығару жайлы ұсынылған болжам нәтиже бермесе, тұлға есеп шартын қайта талдап, жаңа болжам ұсынады.
Тұлға есеп шығару жоспарын жүзеге асырып, есеп талабын қанағаттандырған соң (сұраққа толық жауап берген соң), қорытынды бақылау және талдаумен, есеп шығарудың ортақ әдістері, тәсілдері және амалдарымен байланысты болатын есеп шығарудың жаңа кезеңі басталады. Есеп шығару үрдісінің әрбір кезеңдерінде тұлғаның ой әрекетінің түрлі ерекшеліктері көрініс береді. Есепті талдау және оны шығару жолы туралы болжам жасау кезеңінде ойлаудың бақылаушылық, жасампаздық, белсенділік және даралық қасиеттері көрініс табады. Есепті оны шығару қадамдарының тізбегіне жіктеу кезеңінде ойлаудың қисындылық, сатылық (сабақтастық) және жүйелік қасиеттері маңызды болады.
Осы ойлау қасиеттерінің даму деңгейлерінің үйлесуі тұлғаның физикалық есептерді шығарудағы жетістігін анықтайды. Екінші жағынан,тұлғаның барлық ойлау қасиеттері, тек есеп шығару үрдісі барысында ғана дамиды.
Физикалық есеп шығару үрдісінің психологиялық ерешелігін басқалай да сипаттауға болады. Физикалық есеп шығаратын тұлғаның барлық іс-әрекетін үш түрлі бөліктен тұрады деп қарастыруға болады:
1. Физикалық есеп шығару әрекетінің арнайы бөлігіне тұлғаның қарастырылатын есепті шығару барысында өзінің физикалық және математикалық теориялық білімдерін көкейтестендіруі: бұрынғы есептерді шығарғанда жинақталған өзінің арнайы білімдерін, ебдейліктерін және дағдыларын қолдануы: есеп шартын дұрыс талқылау және қолдану ебдейліктері жатады.
2. Физикалық есеп шығару әрекетінің логикалық (қисынды ) бөлігіне есеп шығару барысында есеп шартын түрлендіру сатысын жүзеге асыру үшін, физика мен математиканың жалпы теориялық ұстанымдарынан қорытынды жасаудың жалпы логикалық ережелерін қолдану жатады.
3. Физикалық есеп шығару әрекетінің эвристиктік бөлігіне есеп шығару тәсілдері ізделетін, есеп шығару сатылары анықталатын жалпы ережелер жатады. Эвристиктер деп аталатын бұл жалпы ережелер ықтималдық сипатты ғана болады. Олар есеп шығарудың ақылға қонымды жолдарын көрсеткенмен, есеп шығару әрекетінің нәтижелілігіне кепілдік бермейді.

ДӘРІС №2. Физика есептерінің классификациясы. Физикалық есеп шығару үрдісінің дидактикалық талдамы.

Физика есептерін: мазмұнына байланысты; берілу тәсіліне қарай; шешу тәсіліне қарай классификациялауға болады (2- кесте).
Есептердің осы түрдегі классификациясының өзі шартты түрде, кейде бірдей есептер классификациялау тәсіліне қарай түрлі топтарға жатқызылуы мүмкін.
Мазмұнына қарай физикада есептерді механика, молекулалық физика, электродинамика т.б. болып бөлінеді. Олар мәтінмен, суретпен, графикпен және сапалық-сұрақ есептермен берілген. Бұл есептер физиканы оқыту әдістемесіндегі қолданылуына, қиындық деңгейіне қарай бөлінеді. Олар жеңіл (жаттығу), орташа және қиын, шығармашылық болып бөлінеді. Жеңіл есептер немесе жаттығу есептері деп бір немесе екі формула қолданып шығаратын, жеңіл тәжірибе жасау арқылы шығарылатын есептерді айтады. Бұл есептерді материалды бекіту үшін қолданады.

2-кесте. Физика есептерінің классификациясы.
Физика есептері
Классификациясы
Есеп түрлері

1. Мазмұнына

а) механика
ә) молекулалық физика және термодинамика
б) электродинамика
в) кванттық физика
2. Берілу тәсіліне қарай
а) мәтінмен берілген
ә) суретпен берілген
б) графикпен берілген
в) сұрақ есептер
3. Қиындығына қарай
а) жаттығу
ә) орташа
б) қиын
в) шығармашылық
4.Шығару әдістемесіне байланысты
а) сапалық
ә) есептеу
б) эксперименттік
в) графиктік

Орташа және қиындау есептер деп бірнеше формуланы, кейде бір тараудағы формулаларды немесе бірнеше бөлімнің формулаларын қолданып шығаратын есептер мен белгілі бір дағдыны керек ететін эксперименттік есептерді айтады. Мұндай есептерді толық тарауды немесе бөлімді қайталанған кезде, оқушылардың білімін нақтылап тереңдету үшін шығарған дұрыс.
Шығармашылық есептердің өзі іздену (яғни, неге деген сұраққа жауап іздейтін) есептер, конструкторлық (яғни қалай жасау керек) есептер болып болып бөлінеді.
Шығармашылық есептер есептер жинағында жұлдызша арқылы ерекшеленіп тұрады. Оларды сыныптағы физика пәнін жақсы оқитын оқушымен жұмыс істеген кезде, олимпиядаларға (мектептегі сынып аралық, мектеп аралық) қатысатын оқушыларға беріп, шығартып үйреткен кезде пайдалануға болады.
Есептің берілу тәсіліне қарай (4 түрге бөледі) мәтінді, графиктік, сұрақ-есептер, сурет-есептер болып бөлінеді. Мұндай бөлінудің өзі шартты түрде, себебі кей есептер суретімен, графиктерімен қоса жүреді.
Есептер шығарылу әдістемесіне байланысты сапалық, сандық немесе есептеу-есептері, графиктік, эксперименттік болып бөлінеді. Мұндай бөліну қажетті және маңызды, себебі мұғалімнің оқушылардың математикалық дайындықтарына қарай есеп таңдауына көп септігін тигізеді.
Сапалық есептердің физикалық құбылыстар мен заңдылықтарды оқып үйренуде маңызы өте зор. Мысалы, тербелісті оқып үйренгенде:
1) Алтыбақанға бір адам емес, екі адам отырса тербеліс периоды өзгере ме?
2) Серіппедегі дененің массасын екі есе арттырсақ, оның тербеліс периоды қалай өзгереді? 3) Егерде дене бекітілген серіппені қатаңдығы бұрынғыдан екі есе артық серіппемен ауыстырсақ, дененің тербеліс периоды қалай өзгереді? - деген сапалық есептерді шығару арқылы тербеліс периодын анықтауға берілген формулаларды оқушылардың естерінде қалдырып, бекітуге болады. Әрі олар оның практикада күнделікті өмірде қолданылуымен танысады.
Сапалық есептердің ерекшелігі мұнда оқушылардың ойын жинақтап, белгілі бір физикалық құбылыстардың мағынасын ашуға көмектеседі. Оларды логикалық ойлау арқылы физиканың заңдылықтарына сүйене отырып шығарады. Мысалы: суға көлемдері бірдей мыс және алюминий кубтар батырылған. Осы кубтарға шама жағынан бірдей кері итеруші күштер әсер ете ме?
Есептеу есептеріне тән қасиет берілген сұраққа жауапты тек математикалық амалдарды қолдана отырып табуға болады. Мұндай есептерді көбінесе жоғарғы сыныптарда қолданады. Шығарылудағы математикалық тәсілдерді қолдануға байланысты есептер арифметикалық, алгебралық, геометриялық болып бөлінеді. Осылардың ішінде көп қолданылатыны - алгебралық.
Есептеу есептері физикада жиі кездеседі. Соның ішінде шамалардың сан-мәнімен берілген есептер көп. Қазіргі кезде есептегіш құралдардың көптігін ескерсек, мұндай есептерді шығару көп қиындық туғызбайды. Әйтседе физика пәнінің мұғалімдері таза физикалық есептерді (шамалардың сан-мәндері берілмеген есептер) уақыт үнемдеу үшін көптеп шығарылғаны дұрыс. Мысалы:
1) Сыйымдылықтары С1 және С2 жазық конденсаторлар 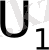және потенциалдар айырымына дейін зарядталған 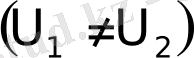. Осы конденсаторларды параллель қосқан кезде олардың электрстатикалық энергиясы кемитіндігін көрсетіңіздер. Неге олай болады?
2) Радиусы және сыну көрсеткіші 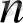мөлдір шарға бір диаметрлерінің бағыты бойынша жіңішке параллель жарық шоғы түседі. Жарық шоғы шар центрінен қандай 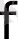қашықтықта қиылысады?
3) Қатаңдығы серіппеге ілінген массасы ыдысқа биіктіктен массасы дене құлайды да ыдыста қалады, яғни оның ыдыс түбіне соғылуын абсолют серпімсіз деп есептеуге болады. Ыдыс пен дене тербеле бастайды. Тербеліс амплитудасын анықтаңыздар (1-сурет).

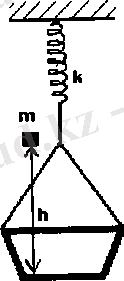
1-сурет

4) Массасы , температурасы Т болатын бір атомды идеал газдың ішкі энергиясын есептеп табыңдар.
Мұндағы төртінші есепті идеал газдың ішкі энергиясы тақырыбын оқып үйренгенде, жаңа материалды өткен кезде, яғни жаңа сабақты түсіндіруге қолдануға болады.
Эксперименттік есептерді шығару үшін, арнаулы құрал-жабдықтардың көмегімен тәжірибе жасап, нәтижесінде алынған шамалар арқылы есеп шығарылады. Эксперименттік есептерді шығару үрдісінде оқушылардың қызығушылығы артып, бақылағыштығы дамып, құрал-жабдықтармен жұмыс істеу дағдылары мен икемділіктері жетіледі. Оқушылар физикалық құбылыстар мен заңдылықтарды тереңірек танып біледі.
Графиктік есептер деп график бойынша берілген есепке керекті шамаларды анықтап шығаруға болатын есептерді айтады.
Графиктік есептерді шығару үрдісінде графиктерді салу, графиктерден қажетті шамаларды тауып, есептеулерде қолдана білуге дағдыланады. Графиктерді салу, тұрғызу кезінде оқушылар физикалық шамалар арасындағы функциялық тәуелділікті түсінуге, ұқыптылыққа үйренеді, яғни олардың танымдық және политехникалық мәні өте зор.

Физикалық есеп шығару үрдісінің дидактикалық талдамы.
Барлық физикалық есептер белгілі бір дидактикалық мақсаттарда шығарылады. Мұндай әрбір мақсатқа есептің нақты бір түрі сәйкес келеді.
Кіріспе - мақсаттану (проблемдік) есептері.
Оқыту нәтижесі болу үшін, оқушылардың білім алуға қажет мақсаттануын қалыптастыру керек. әрбір адамның белгілі бір деңгейдегі ақпарат алу қажеттігі болады. Мұндай ақпараттық қажеттілікті қанағаттандыру тұлғаны рухани байытып, оның тұлға ретінде қалыптасуына ықпал етеді. Ақпаратты қабылдаушы жүйені, қарапайым түрде, ақпараттар алмасу жолын бөгеуші сүзгілер жүйесі ретінде қарастыруға болады. Мұнда жүйеге ( тұлға) кіруші ақпарат пен оған мағынасы жағынан (жүйе ішінде) сәйкес келетін ақпаратты бөліп қарастыру керек. Сөңғысы көптеген сүзгілер жүйесінен өтіп, жүйеден шығардағы ақпарат. Дидактикалық тілде бұл мынаны білдіреді:
Мұғалімнің оқушыларға беретін ақпаратын оқушылар көріп немесе естіп қабылдайды. Бірақ әрбір оқушының сезім мүшелерімен қабылдайтын ақпараты өңдейтін өз "сүзгілер жүйесі" болады. Оқушылар жеткілікті дәрежеде дайын болмаса немесе дұрыс бағдарланбаса қабылданатын ақпараттың оқушы үшін мағнасы болмайды, яғни ақпарат сенімге, намымға, түсінікке, ғылыми көзқарасқа айналмайды.
Сондықтан мұғалімнің негізгі міндеті, оқушылардың алдағы жұмысқа (есеп шығаруға) белсенді қызығушылығын қалыптастыру. Бұл мәселені оқушыларға оқу материалын оқып-білудің және физика саласындағы жаңа ебдейліктерді меңгерудің қажеттігін көрсететін, кіріспе-мақсаттану немесе проблемдік тапсырмалар арқылы шешуге болады.
Проблемдік тапсырма кіріспе сабағында тұжырымдалып, жаңа тақырыпты меңгеру барысында шешілуі мүмкін. Яғни оқушылардың алдына проблемдік мәселе қою мұғалімнің болашақта ұсынатын ақпаратын мағналы ететін жағдай туғызады.
Танымдық есептер.
Психологтар адам алдына мәселе немесе проблем қою ғана, оның санасында ойлау үрдісін туғызатынын дәлелдеген. Яғни, оқу материалын терең игеру үшін, оқушыларға оны есептер жүйесі түрінде жиі ұсыну керек. Сондықтан, оқушылармен бірге белгілі бір құбылыстың физикалық заңдылықтарын оқып-үйренгенде, бұл үрдісті жалпы сипаттағы арнайы таңдап алынған танымдық есептер жүйесін шығару түрінде ұйымдастырған тиімді.
Оқу есептері.
Мұғалім шығарылу жолын көрсететін, жалпы танымдық сипаттағы есептерден басқа, оқушылар нақты - практикалық есептерді шығару әдістерін де меңгеру керек. Мұндай әдістерді меңгеру үшін, оқу есептерін қолдану керек. Оқу есептері - нақты-практикалық есептер, оларды шығару барысында оқушылар берілген тақырыптағы есептер шығарудың жалпылама әдістерін меңгереді. Оқу есептерін шығарудың мақсаты берілген тақырыптағы есептерді шығарудың жалпы әдісін көрсету және берілген әдісті меңгеру.
Жаттығу есептері.
Физиканы оқу барысында оқушылар білім жүйесі мен жалпы ебдейліктерді меңгеріп қана қоймай, іс-әрекеттерді автоматтандыратын дағдылар жүйесін де қалыптастырады. Оқушылардың қандай да бір дағдысын қалыптастыру үшін қарапайым физикалық есептер жүйесін қолдануға болады. Мұндай есептерде қажет дағдыны қалыптастыруға қажет амалды ондаған рет қайталайды.
Бақылау - бағалау есептері.
Оқушының физика курсынан оқу әрекетін (жұмысын) бақылау және бағалау үшін физикалық есептерді қолданады, оларды өздігінен шешу оқушының оқу материалын меңгеру деңгейін сенімді түрде көрсетеді.
Оқу үрдісінде қолданылатын, физикалық есептерді шығару барысында, мұғалімнің жетпек болар негізгі дидактикалық мақсаты осы.
Есеп шығару үрдісінің белгілі бір мақсатқа бағытталуы және түрлі есептерді шығарудың мақсаттары мұғалімге ғана емес оқушыға да белгілі болуы өте маңызды.
Бұл есеп шығаруды бастар алдында, мұғалім, міндетті түрде, есептің қандай мақсатпен шығарылатынын және оны шығару нәтижесінде қандай жетістікке жететінін айтып отыру керек деген сөз. Тек осы жағдайда ғана, оқушылар физикалық есептерді саналы түрде, оның мақсатын толық түсініп шығарады.

ДӘРІС №3. Физикалық есеп шығарудың ТӘСІЛДЕРІ, амалдары. Күрделі есепті шығарылуы белгілі, қарапайым есептерге бөлу амалы. Жаңа есепті шығарылуы белгілі ұқсас есепке келтіру. Қайта нобайлау немесе есепті біртіндеп оңайлайтын есептермен ауыстыру амалы. Оңтайлы санақ жүйесін таңдау амалы. Энергияның сақталу заңын қолдану амалы.

Есеп шығарудың тәсілін таңдау арқылы ғана, есептің жауабын алу мүмкін емес. Ол үшін таңдап алынған тәсілді жүзеге асыру керек, яғни, есептің шартындағы нысандарға және оның сипаттамаларына қажет болатын, логикалық, математикалық немесе тәжірибелік амалдарды қолдану керек.
Есеп шығарудың таңдап алынған тәсілі белгілі бір әдістердің жиынтығы арқылы жүзеге асады. Физикалық есептерді шығару амалдары сан алуан, оларды қолдана білі, оқушылардың есеп шығара алу қабілетін анықтайды.
Көптеген әдебиеттерде есеп шығару амалдарын қарастырмайды, оның орнына әдіс, тәсіл сөздерін қолданады.
Бұл дұрыс емес, себебі әдіс, тәсіл түсініктері есеп шығаруға бағытталған көзқарасты сипаттайды, олар есеп шығарудың жоспарын жасауға көмектесіп, оқушыларды нақты есеп шығаруға қажет ойлау әрекеттерінің тізбегімен қаруландырады, ал есептің шешімі тек белгілі бір амалдар көмегімен ғана алынады.
Күрделі есепті шығарылуы белгілі, қарапайым есептерге бөлу амалы.
Мысалы: Горизонтқа бұрыш жасай лақтырылған дененің ұшу ұзақтығы S, максимал көтерілу биіктігі h. Лақтыру бұрышы α-ны және бастапқы жылдамдық υ0-ді табыңдар (12 - сурет).
Бұл есепті шығарылуы белгілі бірнеше есепке бөлуге болады:
1) дене υ0 жылдамдықпен вертикаль жоғары лақтырылған. Дененің максимал биіктікке көтерілу уақытын табыңдар.
Қозғалыс тең кемімелі υ= υ0 - gt.
h- максимал биіктікте υ = 0, υ0 - gt = 0, t = υ0 g.
1) дененің жоғары көтерілу уақыты тусу уақытына тең екендігін дәлелдеңдер.
Жоғары
;
;
төмен
;
=; ;
vx
х
у
v
vy
α
3 - сурет
3) горизонтқа бұрыш жасай лақтырылған дененің қозғалысын 2 қозғалыс қосындысы түрінде (вертикаль жоғары - g үдеумен және горизонталь бағытта - бір қалыпты) өрнектеуге болатынын көрсетіңіз. v - векторының координаталар өсіндегі прекциясын қарастырайық: а) денеге тек бір ғана күш ауырлық күші - mg әсер етеді. Яғни вертикаль бағыттағы қозғалыс тең кемімелі, үдеу g-ға тең.
ә) горизонталь бағытта ешқандай күш әсер етпейді , дене 0х өсі бойымен инерциямен қозғалады. Қозғалыс бір қалыпты.

vy=v·sinα - gt; vx=v ·cosα .

2) Дененің максимал биіктікке көтерілу уақыты мен горизонталь бағытта ұшу уақытын салыстырыңдар.

t гор= tкөтерілу+ tқұлау=2· tкөтерілу

3) v0 жылдамдықпен горизонтқа бұрыш жасай лақтырылған дене h- максимал биіктікке көтерілді. Лақтыру бұрышын табыңдар.

уақытты vy0 = gt өрнегінен табамыз.

.
Сонымен күрделі есеп шығарылуы белгілі 5 есепке бөлінді. Осыларға сүйеніп бастапқы есепті шығарайық.
Бер: (1)
S
h (2)

қозғалыс соңында h = 0

t1=0 - қозғалыс басталған уақыт.
t2 - ұшу уақыты.
Көтерілу уақыты уақыт мәндерін (1) мен (2) теңдеулерге қойып мыналарды аламыз.

соңғы теңдеулерден α мен υ0-ді аламыз.

Жаңа есепті шығарылуы белгілі ұқсас есепке келтіру. Кей жағдайларда жаңа есеппен бұрын шығарылған есепті салыстыра мыналарды байқаймыз: олардың тек нысандары немесе сипаттамаларының сандық мәндері өзгеше, немесе шамалар басқа бірліктер жүйесінде беріледі. Кейбір есептердің талабы, бұрын шығарылған есеп шарты және керісінше болады.
Бұлар қарапайым ұқсас есептер, олар белгілі бір есептің жекеше түрлері болып табылады.
Мысалдар:
1). Бір бірінен 3см қашықтықта орналасқан шамалары 10нКл екі заряд
қандай күшпен әрекеттеседі.
2). Шамалары 1мкКл және 10нКЛ екі зарядтың әсерлесу күші 9мН .
олардың арақашықтығы қандай?
3). Екі электронның электрлік тебілу күші гравитациялық тартылу
күшінен неше есе артық.
1)

2)

3)

Бұл есептерде ізделінділер әр түрлі. Есеп шығару үрдісін бірдей деп қарастыруға болады. Есеп шарты мен талабының түрлі болуына қарамастан, оқушылар олардың ортақ құрылысын, ұқсас есептерді шығарудың ортақ әдісі мен тәсілдерін байқай білу керек.

Қайта нобайлау немесе есепті біртіндеп оңайлайтын есептермен ауыстыру амалы. Бұл амалды қолдану мысалына күрделі электр тізбегін есептегенде эквивалент кескіндерді құрастыру әдісін жатқызуға болады. Мұндай есептерде қайта нобайлау амалы есепті қарапайым есептерге бөлу амалымен үйлеседі.
1 - мысал: 4 - суреттегі тізбектің жалпы кедергісін табыңдар.
2R
3R
2R
3R
B
A
5 - сурет

2R
3R
2R
3R
B
A
R
C
D
4 - сурет
С және D нүктелерінің потенциалдары бірдей, себебі тармақтар симметриялы. Сондықтан R - кедергіден ток жүрмейді, сол себепті С және D нүктелерін ажыратуға болады. Яғни, мынандай эквивалент кескін аламыз.
5R
5R
B
A
6 - сурет
Бұл суретте тізбектей жалғанған 2R және 3R тізбектен тұратын ACB және ADB тармақтар бір бірімен параллель жалғанған. Тізбектің қарапайым кескіні мынандай болады: Бұл тізбектің жалпы кедергісін табу оңай:

A
A1
D1
B1
C1
D
B
C
7- сурет
2 - мысал: Әр бір қырының кедергісі R болатын куб тәріздес тізбектің жалпы кедергісін табыңдар (7 - сурет).Кубтың A1,D,B нүктелерінің потенциалдары бір біріне тең. D1,B1,C нүктелерінің потенциалдары да бір біріне тең болады. Потенциалдары бірдей нүктелерді бір бірімен қосып 8 - суреттегідей эквивалент кескін аламыз. Бұл тізбектің кедергісі оңай табылады:

R
R
R
R
R
R
R
R
R
R
R
R
C1
A
A1
D B
B1
C D1 D
8 - сурет

Оңтайлы санақ жүйесін таңдау амалы. Координаттар жүйесін таңдау есеп шартына байланысты болады.
1 - мысал: Массасы 400 г. білеуше, массасы 100 г. жүк әсерінен 2с.-та 8 см. жол жүреді (9 - сурет). Үйкеліс коэффициентін табыңдар.
Есеп шартын идеалдау: Екі дене салмақсыз шығыр бойымен қозғалатын созылмайтын жіппен жалғанған, сондықтан Т1 = Т2 . Массасы үлкен бірінші дененің горизонталь бетпен үйкеліс коэффициенті тұрақты.

x
y
T1
N
Fү
m1 g
T2
m2 g
9 - сурет
Бер: Шешімі:
Т1 = T2 = T Денеге әсер етуші күштер суретте көрсетілген.
m1 = 0,4 кг Қозғалыстағы денелер үшін координаттар өстерін
m2 = 0,1 кг таңдайық. Бірінші дене горизонталь бағытта таңдайық.
S = 0,08 м Бірінші дене горизонталь бағытта ғана қозғалады,
t = 2 c сондықтан Х - өсін бірінші дененің қозғалыс бағытымен
v0 = 0 бағыттаймыз. У - өсін екінші дененің қозғалыс a1 = a2 = a
бағытымен бағыттаймыз.
μ - ?

Есептің шығарылуы төмендегі түрлендірулерден түсінікті болады:
m1 g + N + Fү + T = m1 a
m2 g + T = m2 a

Fү = μ m1 g

X: T + μ m1 g = m1 a
У: m2 g - T = m2 a

Белгісіз а - үдеуді қозғалыс теңдеуінен анықтаймыз:

Жауабы: μ= 0,25

2 - мысал: Білеуше көлбеулік бұрышы 300 көлбеу жазықтық бойымен сырғанайды. Үйкеліс коэффициенті 0,2 болса, дене қандай үдеумен қозғалады?
Шешуі: Мұндай есептерді шығарғанда кординат өстерін көлбей жазытықты бойлай және оған перпендикуляр бағытта таңдау керек. Өстің басқа бағыттарын таңдау есепті қиындатып жібереді.

x
Fү
mg
N
y
10 - сурет
α

Бер: Шешімі:
α = 30[0] m g + N + Fү = m a
μ = 0,2
Fү = μN = μ m g
a - ? х: mg Sin α - Fү = ma
у: N - mg Cos α = 0

N = mg Cos α
Fү = μ m g Cos α

mg Sin α - μ m g Cos α = ma

a= g (Sin α - μ Cos α)

a = 10 ( 0,5 - 0,2· 0,866) ≈ 3,2 (мс)

Жауабы: a = 3,2 мс

Энергияның сақталу заңын қолдану амалы. Энергияның сақталу заңын қолдану кейбір есептерді оп-оңай шығаруға мүмкіндік береді.
1 - мысал. Толық массасы - m шана биіктігі - h, ұзындығы - l төбеден сырғып түседі (11 - сурет). Шананың бастапқы жылдамдығы нөле тең, ал етекке түскендегі жылдамдығы - v, болса шана қозғалысына орташа кедергі күшті табыңдар.
X
a
Fк
mg
l

h
N
y
11 - сурет
H
L
v0 =0
V

Fк - ?

а) Есепті Ньютонның екінші заңын қолданып шығарайық:
N + mg + Fк = ma
y: N - mg·cosα = 0
x: mg·sinα - Fк = ma

Fк = m(g·sinα - a)

sinα =h l

S = (v2 - v02) 2a

a = v2 2S

S = l

ә) Есепті энергияның сақталу заңын қолданып шығарайық: Бастапқы мезетте шананыңпотенциялық энергиясы
Еп = mgh
Тау етегіндегі кинетикалық энергия
Ек = mv2 2
Энергия өзгерісі кедергі күшінің жұмысына тең болады:
А = Fк l = Еп - Ек
Fк l = mgh - mv2 2

2- мысал. Дене 30мс жылдамдықпен тік жоғары лақтырылған. Қандай биіктікте және қанша уақыттан кейін дене жылдамдығы 3 есе кемиді.
1-тәсіл
v0 = 30 мс v= v0 - gt ; t = (v0 - v) g = 2v0 3g
v = v0 3 = 10 мс
h = v0 t - gt2 2 = v0 · 2v0 3g - (g2)·(2v0 3g)2
h - ? , t - ?
h= 4v02 9g

t = 2 c.; h = 40 м.

2- тәсіл
mv02 2 = mgh - mv 2

mgh = mv02 2 - mv 2

h = 4v02 9g = 40 (м)

h = v0 t - gt2 2

t1 = 2 c.
ДӘРІС №4. Физикалық есептер шығару үрдісінің кезеңдері. Физикалық есептердің мазмұны мен құрлысын талдау.

Кез келген физикалық есеп шығару үрдісі - бұл 5 кезеңнен тұратын, күрделі ойлау әрекеті.
1) Есептің құрылымы мен мазмұнын талдау кезеңі. Ол есептің белгілі бір кескіндік таңбалық нобайын (сурет, кескін, шарт) жасаумен аяқталады.
2) Есептің шығару жолдарын іздеу кезеңі. Бұл кезең есепте қарастырылатын физикалық құбылыс немесе үрдіс анықталып, физикалық заң, формула еске түсіріліп, физикалық есептің математикалық нобайын жасаумен аяқталады.
3) Таңдап алынған есеп шығару әдісін жүзеге асыру кезеңі. Бұл кезеңде есеп шығару тәсілдері мен математикалық аппарат таңдап алынып, математикалық амалдар орындалады. Кезең есептің шешімін (жауабын) алумен аяқталады.
4) Алынған нәтиженің дұрыстығын, ақиқатқа сайлығын, өлшемдерінің сәйкестігін т.с.с. талдау кезеңі.
5) Есеп шығару үрдісінің, оқу-танымдық талдамын жасау кезеңі. Бұл кезеңде есеп шығару әдісінің, қоданылған тәсілдің маңызы бағаланып, қарастырылған есепке ұқсас есептерді шығарудың жалпы (ортақ) әдісі көрсетіледі.
Бұл кезеңнің оқу-танымдық маңызы ерекше, себебі алуан түрлі есептердің ішіндегі нақты бір есепті шығауда қолданылатын әдістер мен тәсілдерді жалпылауға мүмкіндік береді.

Физикалық есептерді шығарң кезеңдері
12-сурет
Физикалық есеп
1. Есепті талдау
Физикалық мазмұндық талдау
Құрылымды-логикалық талдау
Физикалық идеалды нобай
Құрылымдық нобай
Кескінді таңбалы нобай
2. Есеп шығару жолдарын
іздеу
Есепті қайта
нобайлау, қайта тұжырымдау
Физикалық заңдар, формулалар, тұжырымдар
Есеп шығару жолда- рын психолгиялық талдау
Есептің математикалық нобайы

Есеп шығарудың әдісін, амалын, тәсілін таңдау

Математикалық амалдарды жүзеге асыру
3. Есеп шығару әдісін жүзеге асыру, (шешімді табу)
Математикалық ап- парат пен логикалық ережені таңдау
Нәтиженің өлшемі
4. Нәтиже дұрыстығын талдау
Шамалар нақтылығы
Таңдап алынған есеп шығару әдісінің маңызы, басқа тәсіл іздеу
5. Есеп шығару үрдісін оқу - танымдық талдау
Ұқсас есептерді шығарудың ортақ әдістерін көрсету
Физикалық есеп шығару үрдісінің сұлбасы 12 - суретте келтірілген. Бұл кескін есеп шығарудың күрделі және сан қырлы үрдіс екенін көрсетеді. Есептерді шығарғанда барлық кезеңдерді қарастыру міндетті емес. Есептің түрі, мазмұны күрделілігіне байланысты, есеп шығару үрдісінің кейбір кезеңдері түсіп қалуы, ал кейбір кезеңдерінің түрі мен мазмұны өзгеруі мүмкін. Қарастырылған кезеңдер бір бірінен нақты бөлінбеген, олар көбіне бір бірімен қиылысып жатады.

Физикалық есептердің мазмұны мен құрылысын талдау.
Физикалық есептерді шығару үрдісінің кезеңдерін қарастыр, есептердің мазмұны мен құрылысын талдаудың өте маңызды екенін көрсетеді. Осы кезеңде есептердің түрі және шарты айқындалады.
Физикалық есептерді талдаудың толықтығы мен тереңдігі есептің түріне ғана емес, оқушылардың білім, дағды және ебдейліктеріне де байланысты болады.
Оқушылардың қарастырылатын есептер түрімен таныс болуы және ондай есептерді шығарудың ортақ әдістерін білуі бір мәселе. Ал берілген есептің оқушыларға таныс болмайтын жағдайы екінші мәселе.
Физикалық есептерді талдаудың әдістері мен жолдарын қарастырайық. Физикалық есептерді талдау үрдісін бірнеше кезеңдерге бөлуге болады:
Бірінші кезең есептің құрылымдық-логикалық талдауы мен оның құрылысын анықтаудан, яғни, құрылымдық элементтер (есеп нысандарын) мен олардың сипаттарын (параметрлерін) айқындаудан тұрады.
Кейбір нысандар бірден айқындалады, ал кейбіреулерін толық талдаудан кейін ( олар жасырын нысандар деп аталады) белгілі болады. Нысан сипаттары да осылай аталады.
Екінші кезең нысандар арасындағы байланысты және есепте қарастыратын жағдайдың негізі болатын физикалық құбылыстар мен үрдістерді анықтаудан тұрады. Бұл кезеңде есептегі нысандар сипаттамалары арасындағы логикалық және функционал қатыстар (сандық және сапалық) анықталады.
Үшінші кезеңде нақты физикалық нысандар идеал нобайлармен ауыстырылады. Кезең идеал есеп қарастырумен анықталады.
Төртінші кезеңде қарастырылатын есептің мазмұны мен құрылысының көрнекі кескіні (сызбалар, суретттер, диаграмдар және т.с.с.) қарастырылады.
Бұл кезең есептің қысқаша шартын жазумен аяқталады. Есептің қысқа шартын, берілген есептің кескіндік таңбалық нобайы деп те қарастыруға болады.
Физикалық есептің түріне және есеп шартының сипатына байланысты талдау кезеңдері толық болмауы (талдаудың тек жинақталған түрде өтуі) мүмкін екендігін айта кету керек.
Сонымен, физикалық есепті шығару дегеніміз:
1) физиканың жалпы теориялық тұжырымдарын ( анықтамалар, заңдар, формулалар) және математиканың ережелері мен амалдарын тауып, оларды есеп шартына және есеп шығару үрдісінің аралық нәтижелеріне қолданып, есеп талабын қанағаттандыру.
2) Қарастырылатын есептегі нақты құбылысты, физика теориясында заңдылықтары мен формулалары тағайындалған идеал құбылыспен ауыстыру.
3) Шешуі физикалық есептің де шешуі болатын математикалық есептер құрастыру.

Мысалы: Биіктігі 10 см ұзындығы 50 см көлбеу жазықтықта массасы 2 кг білеу тыныш тұр. Динамометр көмегімен денені алдымен жоғары сүйреп шығарды, сонансоң төмен сүйреп түсірді. Екі жағдайдағы динамометр көрсетулерінің айырмасын табыңдар.
1) Есеп мазмұнын талдау
Бірінші саты: Есептегі құрылымдық нысандар: білеу, көлбеу жазықтық, көлбеулік бұрыш, динамометр.
Сипаттамалары: (айқын берілгендер) ұзындық - l, биіктік - h, масса - m; (жасырын берілгендер) үйкеліс коэффициенті - μ.
Екінші саты: Есепте қарастырылатын құбылыс немесе үрдіс - дененің көлбеу жазықтық бойымен үйкеліспен қозғаласы. Құбылыстың жасырын сипаттамалары: μ = const., a = const., яғни v = const.
Үшінші саты: Идеалдау:
а) үйкеліс коэффициенті μ = const;
ә) білеудің өлшемдері өте кіші;
б) нақты жағдайда үйкелуші денелер қызады, оны ескеру есеп шығаруды қиындатар еді.
Нәтижеде мынандай идеал есеп аламыз: Массасы 2 кг дене динамометр көмегімен, биіктігі 10 см ұзындығы 50 см көлбеу жазықтық бойымен жоғары төмен бір қалыпты қозғалады. Үйкеліс коэффициентін тұрақты деп есептеп динамометр көрсетулерінің айырмасын табыңдар. Ауа кедергісі мен денелердің қызуы ескерілмесін.
Төртінші саты:
а) таңбалы нобай: ә) кескіндеуші сурет
v
Fү
mg
N
F
13 - сурет
l = 0,5 м
h =0,1 м
m = 2 кг
v = const
μ = const

ΔF - ?
2) Есеп шығару жолын іздеу
ΔF = F1 - F2
Есепті ньютонның екінші заңын қолданып шығарамыз:
F + N +mg +Fү = 0
Есеп шығарудың бұл кезеңі жинақталған, себебі суреттен есеп шығару жолы көрініп отыр. Бұл - есеп шығарудың аналитик (өрнектерді түрлендіріп талдау) әдісі.
F1 - Fү - mg Sin α = 0

- F2 + Fү - mg Sin α = 0

ΔF = 2mg Sin α
3) Есепті шығару:
ΔF = 8 Н.
4) Өлшемді тексеру:
5) Оқу - танымдық талдау:
Есептің пайдасы мынада: ол оқушыларға суретті дұрыс салуды, күштерді белгілеуді және күштердің координата өстеріндегі проекцияларын салуды үйретеді. Мұндай есептердегі ең маңызды мәселе - Ньютонның екінші заңын векторлық және скаляр түрде жазу.
Физикалық есеп және оның құрылысы.
Усова мен Бобров есептің барлық анықтамаларын талдай отырып мынадай қорытынды жасайды: "Физикалық есеп - физиканың заңдары мен әдістеріне негізделіп, физикалық білім алу мен ақыл-ойды жетілдіруге бағытталған, оқушылардан ой және практикалық іс-әрекетті талап ететін - жағдай ( белгілі фактлердің жиынтығы)".
Қандай есеп қарастырмайық, олардың құрылысы бірдей болады:
1) Кез келген есепте бір немесе бірнеше нысан (зат, құбылыс, үрдіс) қарастырылады.
2) Есеп мәтінінде бір немесе бірнеше тұжырым (шарт) және бір немесе бірнеше талап болады, олар сұрақ түрінде қойылуы мүмкін.
3) Есеп шартында нысандардың сипаттары мен қатынастары келтіріледі.
Кейде есеп шарты нақты берілмейді, оларды есепті терең жан-жақты талдау барысында анықтайды.
Есепте кездесетін нысандар сипаты мен қатынастарын 14 - суреттегі кескін арқылы жүйелеуге болады14 - сурет
айқын(нақты)
сандық
анық
ізделінді
анықталмаған
аралық
белгісіздер
сапалық
жасырын
Есеп нысандары мен сипаттарының қатынастары қатынастары.
4). Есеп талабы негізгі үш түрден тұрады.
4.1. Ізделінді шаманы табу ( тағайындау, анықтау). Мұндай талаптары бар есептерді, ізделінді шаманы табуға арналған есептер дейді.олар сандық және сапалық болып екіге бөлінеді;
3.2. Белгілі бір қасиеттің немесе қатынастың бар не жоқ екендігін дәлелдеу, түсіндіру. Дәлелдеу есептері.
3.3. Нысанды құрастыру, жасау, түрлендіру. Мұндай талабы бар есептерді салу (құрастыру) есептері дейді.
Қарастырылған төрт құрылымдық бөліктерді біріктіре есеп тұжырымы (мәтіні) дейді.
Келесі есеп құрылымын, оны шығармай, қарастырайық..
Мысал: Температуралары -10ºС болатын екі мұз кесегі соқтығысқан соң түгелдей буға айналу үшін, бір-біріне қарай қандай жылдамдықпен қозғалу керек?
1. нысандар: 2 мұз кесегі.
2. Тұжырымдары: а) мұз жылдамдықтары бір-біріне қарай бағытталған
ә) мұз температуралары t = -10ºС
3. Сипаттамалары: а) нақты: t = -10ºС (сандық) ; υ01= υ02 (айқын)
ә) нақты берілмегендер:
Сандық және айқын
Сапалық
Мұз массалары m1 = m2
мұздың соңғы жылдамдықтары υс1= υс2 = 0;
аралық температура t1 = 0ºС;
соңғы температура tс = 100ºС.

Мұздың кинетикалық энергиясы жылуға айналады Ek=Q,
Соқтығысқан кезде мұз кесектері 0ºС-ге дейін қызады , одан кейін ериді, пайда болған су 100ºС-ге дейін қызады одан кейін буға айналады. Сондықтан біз физикалық шамалардың кестелік мәнін қолданамыз: см, λ, сс, r.
4. Талап: v-жылдамдықтың сандық мәнін есептеу.
Келесі мысал: Су ішіндегі массасы 30кг , көлемі 0,012м3 тасты көтеру үшін қандай күш жұмсау керек?
1. Нысандар: тас, су, арқан.
2. Тұжырым: тас су ішінде жатыр.
3. Сипаттамалар:
а) нақты, сандық mт =30кг Vт =0.012м3.
ә) нақты берілмеген, сандық ρс =1000кгм37
б) сапалық: су ішіндегі тасқа: Fa=mтg (ауырлық күші) ;

FА
Fk
Fa
15 - сурет.

FА= ρсgVт (Архимед күші); Fk - (керілу) күштері әсер етеді (15-сурет) 4. Талап: Керілу күші Fк-нің сандық мәнін табу.
Есептерді жүйелеу. Физикалық есептерді әр түрлі белгілері бойынша жүйелеуге болады:
1) Есеп шартының берілуі бойынша: мәтіндік, графиктік, сурет-есеп, тәжірибелік-есептер;
2) Күрделілік деңгейі ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.