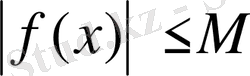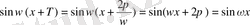Тригонометриялық функцияларды жетілдіре оқыту жолдары

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 32 бет
Таңдаулыға:

Кіріспе

Математика ілімі ежелгі заманнан бүгінгі күнге дейін адам баласына
қалтқысыз қызмет етіп келеді. Математика жетістіктері мен компьютерді барша
ғылым саласында, өмірде пайдалану-қазіргі заманның басты сипатына айналып
отыр.
Математиканы оқыту әдістемесі – пәннің мақсаттарын қоғам талаптарына
сай іске асырып, оның заңдылықтарын тәуелді бірлік негізінде зерттейтін
ілім.
Математиканы оқыту әдістемесі белгілі мағынада педагогикамен,
логикамен, психологиямен, физиологиямен, информатикамен ұштасып жатады.
Сондықтан ол өз дамуында екі қиындыққа кезігеді. Бірі – ғылым ретіндегі
математика мен пән ретіндегі математиканың бір-бірінен алшақтығы, екіншісі
– математиканы оқыту әдістемесінің басқа пәндермен сыбайластығы,
жапсарластығы.
Мәселен, тригонометрияның даму тарихын білу, оны зерттеу
–тригонометриялық ұғымдардың даму жолын, әдістерін, бір-бірімен байланысын
тереңірек білуге мүмкіндік жасап, мектептегі тригонометрияны оқытудың
индуктивтік және дедуктивтік жолын қалайды. Оларды қазіргі математика
табыстары мен қоғам талаптарына сәйкестеп, тәжірибе мен дидактикалық
өндеуден өткізіп, тексеру қажет.
Ұзак уақыт бойы тригонометрия геометрияның бір бөлімі ретінде дамып
келді, яғни тригонометриялық функциялардың терминдеріндегі өзіміз
тұжырымдаған фактілер геометриялық ұғымдар мен тұжырымдамалардың көмегімен
тұжырымдалып, дәлелденген. Бәлкім, тригонометрияның дамуына деген үлкен
ықылас практикалық жағынан зор маңызы бар астрономия есептерін (мысалы,
кеменің тұрған жерін анықтауға, күннің, айдың тұтылуларын алдын ала есептеп
шығаруға арналған есептер және с.с.) шығаруға байланысты пайда болған
шығар. Астрономдарды сфера бетінде жатқан үлкен дөңгелектерден құралған
сфералық үшбұрыштардың қабырғалары мен бұрыштарының арасындағы қатыстар
кызықтырды.
Қандай жағдайда болса да, тригонометрияның өзімізге белгілі көптеген
формулаларын геометриялық пішінде ашқан және қайталап өңдеген ертедегі
египет, үнді, араб математиктері.
К. Птолемейдің алғаш рет синустардың кестелерін (ол көп уақыт
хордалар кестелері деп аталып жүрген) құруының зор принциптік маңызы болды:
бірқатар қолданба есептерді әсіресе, астрономия есептерін шығарудың
практикалық құралы жарық көрді.
Дайын кестелермен жұмыс істегенде немесе калькуляторды пайдаланғанда,
біз көбінесе кестелер әлі ойлап табылмаған кездердің де болғанын естен
шығарып аламыз. Оларды құру үшін аса көлемді есептеулерді орындап қана
қоймай, кестелерді құрудың тәсілдерін де ойлап табу қажет болды. Птолемей
кестесі бес ондық үлес таңбаларын қоса алғандағы дәлдікпен жасалған.
Тригонометрияны қазіргі кездегі түріне келтірген ХVІІІ ғасырдың ірі
математигі Л.Эйлер (1707-1783) еді, ол негізі швейцариялық, ұзақ жылдар
бойы Ресейде жұмыс істеген және Петербург ғылым академиясының мүшесі
болған. Тригонометриялық функциялардың белгілі анықтамаларын енгізген де
Л.Эйлер, кез келген бұрыштың функциясын қарастырып, келтіру формулаларын
шығарып алды. Мұның барлығы Эйлердің ұзақ өміріндегі математика үшін жасап
үлгергендерінің азғантай ғана бөлігі: ол 800-ден артық еңбек қалдырған,
математиканың сан алуан салаларына қатысты, көбі классикалық болып қалған
теоремаларды дәлелдеді. Алайда, егер біз геометриялық пішіндегі
тригонометриялық функцияларға сүйеніп, яғни Эйлерге дейінгі математиктердің
көптеген ұрпақтары істегендей жұмыс істеуге тырыссақ, сонда ғана Эйлердің
тригонометрияны жүйеге келтіруге қаншалық еңбек сіңіргенін бағалай алар
едік. Эйлерден кейін тригонометрия есептеу түріне келді: әртүрлі фактілер
тригонометрия формулаларын немқұрайлы қолдану жолымен дәлелдене бастады,
дәлелдеме біршама ірге теуіп, ықшамдалды.
Еліміздің орта мектеп мұғалімдерінің алдында қазіргі заман талабына
сай жан – жақты, орта білімді азаматтарды тәрбиелеп шығару міндеті тұр.
Қазіргі кезде оқу-тәрбие процесін үйлестіруге бағытталған және
сонымен қатар психологиялық – педагогикалық ғылымды тұтасымен қарқынды
дамуға жетелейтін алдыңғы қатарлы педагогикалық тәжірибенің көптеген
жетістіктері белгілі. Бұл өзекті мәселелерге: оқушыларға түсетін
ауыртпашылықты жою, олардың бойында оқуға деген қызығушылықты, белсенділік
пен өз бетінше жұмыс істеу қабілетін тәрбиелеу т.б.
Жалпы білім берудің мақсаты мен міндеті қоғам сұранысы мен қоғамның
мектепке қойып отырған міндеттері арқылы анықталады. Бұл мақсаттар мен
міндеттер заман талабына сай өзгеріп отырады.
Жалпыға бірдей орта білім беру жағдайларында оқу процесін
ұйымдастырудың ең маңызды ерекшелігі барлық оқушылармен осы бағдарламада
көрсетілген математикалық дайындықтың міндетті нәтижелерінің жоспары
олардың жетістіктерін үнемі бақылап отыруда, артта қалғандарға тиісті көмек
көрсетуді қамтиды. Сонымен бірге, барлық оқушыларды оқытуды міндетті
талаптардың ең аз дегенмен шектеп қоюға болмайды: бұл жерде оқушылардың
математикалық қабілеттерін неғұрлым толығырақ аша түсуге талпыну керек. Осы
жағынан алғанда математикалық дайындықтың міндетті деңгейі оның төменгі
шекарасын анықтайды, соның негізінде оқушылардың математикалық ой өрісінің
дамуы одан әрі жүзеге асырылуы тиіс. Осы жағдайларға байланысты математика
мұғалімі жай ғана мұғалім болып қалмай, ол мұғалім тәрбиеші болуы міндетті
және оның негізгі күш жұмсайтын бағыты: оқушылардың жеке дара қасиеттерін
тәрбиелеу, оқыту процесінде оқуға деген құштарлықтарын қалыптастыру, оқудың
мәдениеті және білімді азамат болу үшін қажеттігін түсіндіру тиіс.
Мұғалім еңбегі талмай, тынбай, үнемі ізденісті, жаңалықты,
жаңашылдықты талап ететін қиын да, қызықты жұмыс.
Математика мұғалімі тригонометрияны оқытудың жалпы заңдылықтарын,
мақсаттары мен мазмұнын, әдістемелік зерттеулерді, оқытудың әр түрлі әдіс
тәсілдерін қолдана білуді, педагогика ғылымы мен озат тәжірибе
жетістіктерін мектеп тәжірибесіне батыл енгізу тәсілдерін білуі және
қолдана білуі керек.
Тригонометрияны оқытудың білімдік мақсаты барлық оқушыларды
математика ғылыми негіздері туралы жүйелі білімдермен және оларды толық,
сапалы да берік игеруге қажетті біліктіліктермен, дағдылармен қаруландыру
болып табылады. Осындай білім алу нәтижесінде оқушылардың ақыл ойы дамиды.
Оқу үрдісі мұғалім мен оқушының арасындағы білім алу үшін қойған
мақсатқа, талапқа бірлесіп жететін әрекетті, яғни оқу үрдісі оқыту мен
үйренудің өзара байланысынан тұрып, олардың бірлігі мен алға қойған
мақсаттың орындалуымен анықталады.
Сапалы білім беру үшін пәнді оқутудың әдістемелік жүйесін жасап, оны
практика жүзінде іске асыру қажет. Дидактикалық жағынан оқу үрдісі оқушының
білімді меңгеру міндетіне, ал жеке қарағанда психологиялық дайындығына
байланысты.
Еліміздегі ғалым ұстаздар әр бөлімнің түрлі пәндеріне салалы бағытта
негізделген бағдарламалар құрып, оларға сәйкес оқулықтар, оқу құралдарын
баспадан шығарып жатыр. Ана тілімізде оқытылатын қазақ бөлімдерінде
жазылған бағдарламалар мен сәйкес оқулықтармен жабдықталуы жақсы жолға
қойылып отыр.
Мектептегі тригонометрия курсының практикалық маңыздылығы оның
объектісі кеңістігіндегі пішіндер мен нақтылы болмыстың сандық қатынастары
екенінде болып отыр.
Тригонометрияның теориялық негізін есеп түрінде меңгеру оқушылардың
ойын белсендіреді, икемділік, жылылық, тереңдік, жүйелілік және тағы басқа
қажетті қасиеттерді де қалыптастырады.
Тригонометриялық есеп оқушылардың ұғымдарды, теорияны және шешу
әдістерін меңгерудің тиімді де, айырбасталмайтын құралы болып табылады.
Есеп оқушылардың логикалық ойлау, кеңістікті елестету, жеке бас
қабілеттерін дамытуға бірден бір себепші болатын басты құрал.
Оқушылардың тригонометриядан алған білімінің сапасын арттыру үшін
оларды есеп шығару үрдісінің іс әрекетіне қалыптастыру қажет. Есеп шығару
барысында есеп шығару жолдары мен тәсілдеріне талдау жасауды, есептердегі
ұқсатықтарды көруді, шығарылған есепті теориялық негіздеуді және өздігінің
іс әрекеттерін бағалауды білмейді. Кез келген есепті шығарудың іс әрекеті
уақытылы қалыптаспағандықтан, олар осы әрекеттерді есеп шығару кезінде
үйренеді. Ал бұл кейбір оқушыларға қиындық туғызады. Олардың көпшілігі есеп
шығаруды оның жауабын алу үшін жасалған іс әрекет деп түсінеді. Ал есеп
шығара білу оқушылардың математикалық білім сапасы мен тақырыпты терең
түсінгендігінің көрсеткіші.
Тригонометриядан білім деңгейін тексергенде өтілген тақырыптардан
міндетті түрде есеп шығара білу біліктілігі талап етілуі осыдан шығады.
Мектеп қабырғасында есеп шығаруды үйренбеген оқушылар математика пәніне
үреймен қарайды. Себебі, оларда математика өте қиын, мен бәрібір ұқпаймын
деген ойдан өзіне өзі сенімсіздік қалыптасқандықтан, олардың қиындықты
жеңуге ұмтылу дағдылары жоқ.
Оқушылардың тригонометриядан алған білімінің сапалылығына оқушылардың
бір есепті бірнеше жолмен шығара білуге үйрету арқылы жетуге болады.
Себебі, бұл әрекет барысында ол әр түрлі тақырыпты қайталауға, оларды
байланыстыруға, сонымен қатар алынған нәтижелерді салыстыруға үйренеді.
Тригонометрияны меңгеруге себепші болатын оқушылардың төмендегі
дағдыларының үйлесімін қарастырайық:
1. Тригонометрияға деген оқушы назарының дұрыс бөлінуі, бейімділігі
және әуестігі;
2. Еңбекқорлық, өз бетінше жұмыс істеу, мақсатқа ұмтылушылық және
табандылық сияқты сипаттамалық ерекшеліктері;
3. Белгілі бір жұмысты орындау үшін қолайлы психикалық жағдайлардың
бар болуы;
4. Белгілі бір жұмысты атқару барысында білім қорының, іскерліктің
дағдысының анықталуы немесе ашылуы;
Осы айтылған дағды үйлесімі оқушылардың математикалық қабілетінің
анықталуына көмекші болады, ал қалған қасиеттер оқушылардың кез келген
салаға қатысты қабілетінің айқындалуына көмекші бола алады.
Тригонометрия ғылым ретінде есептен пайда болған және есеп арқылы
дамиды. Тарихқа жүгінсек, ең көне математикалық ескерткіштер Ринд және
Мәскеу папирустарында есептер қарастырылып, оларды шығару жолдары берілген.
Есеп шығару мұқтаждығынан мүмкіншіліктер теориясы, ойындар теориясы,
информатика теориясы т.б. дамыды.
Мектеп тригонометриясын есепсіз құру мүмкін емес. Тригонометрияны
оқытудағы басты мақсаттарға жетуге есеп басты қызметші болып табылады.
Сондықтан тригонометрия сабақтарының жарты уақыты есеп шығаруға арналады.
Әрбір мектеп бітіруші оқушы орта есеппен мыңдай есеп шығарады екен. Ал
солардың көпшілігі жоғары және арнаулы орта оқу орындарына түсу
емтихандарында тригонометрияндан берілген тапсырмаларды шығара алмай
жатады. Бұл әлі де мектеп тригонометриясын оқытуда есеп шығаруға көңіл аз
бөлініп отырғандығының дәлелі.
Есеп шығару ерекше жұмыс, дәлірек айтсақ, ой жұмысы. Ал кез келген
жұмысты дұрыс атқару үшін, оның неден тұратыны және оны орындау үшін қандай
құрал, әдіс керек екенін алдын ала анықтап алу қажет. кез келген есеп
шарттардан және талаптардан құралады.
Есеп шығаруға төмендегідей талаптар қойылады:
а) қатесіз шығару;
ә) негіздеу (дәлелдеу);
б) толық шығару;
в) мүмкіндігінше тиімді жолмен шығару.
Есептің негізгі міндеттері: оқыту, тәрбиелеу, дамыту және бақылау
болып табылады. Барлық есептер оқыту міндетін орындайды. Басқаша айтқанда
кез келген есепті шығарғанда оқушы тригонометриялық білім алады, шығару
біліктілігі қалыптасады, дағдыға ие болады, яғни математикалық білім
деңгейі жоғарылайды. Көбінесе әр есеп өзінің мазмұны арқылы тәрбиелік
міндетін атқарады.
Оқу үрдісінде есеп шығару тригонометрияны оқытудың мақсаты ретінде
де, оны оқыту әдісі ретінде де бой көрсетеді. тригонометриялық есеп
дегеніміз – тригонометрияғы заңдылықтар, ережелер мен әдіс тәсілдер
негізінде оқушылардың ойы мен іс әрекетін талап ететін және
тригонометриялық білімді меңгеруге, оларды практикада қолдана білуге
дағдыландыруға, ойлау қабілетін дамытуға бағытталған ситуация. Сондықтан,
есеп шығару тригонометрияны оқытудың ажырамас бөлігі, себебі есеп шығару
тригонометриялық ұғымдарды қалыптастырып, байытуға оқушылардың
математикалық ойлауын өрістетуге, білімдерін практикада қолдануға,
табандылық, ізденгіштік, еңбексүйгіштік қасиеттерін тәрбиелеуге жол ашады.
Тригонометриялық есептер: а) жаңа тригонометриялық ұғымдар мен
мағлұматтарды үйрету; ә) практикалық іскерліктер мен дағдыларды
қалыптастыру; б) білімнің тереңдігі мен баяндылығын тексеру; в) проблема
қою және проблемалық ахуал туғызу; г) материалды пысықтау; д) оқушылардың
шығармашылық қабілеттерін тәрбиелеу үшін пайдаланылады.
Орта мектеп көлеміндегі тригонометрияны оқытуға қажетті қабілеттілік
оқу материалын шығармашылықпен меңгеруге және есептерді өз бетінше
шығармашылықпен шеше білу қабілеті деп түсінеміз.
Алайда, тригонометриялық есептерді шығару оқушының шығармашылық
белсенділігіне байланысты. Сондықтан, есеп шығарудың басты маңызының бірі
оқушылардың ойлау қызметін жандандыру. Демек, мұғалім оқушылардың ойлау
қызметін жандандыру арқылы оларға әр алуан салуларды, түрлендірулерді,
есептеулерді орындауды, тригонометриялық сөйлемдерді тұжырымдауды үйренумен
бірге, оларды ойлап, талқылауға, тригонометриялық фактілерді салыстыруға,
ортақ немесе айрықша қасиеттерді көрсетуге, дұрыс қорытынды жасауға баулуы
тиіс.
Математикалық ойлауды өрістету үшін оқушылардың қызығушылығын,
ынтасын арттыратын есептерді құрастыру дұрыс. Ондай есептерге зерттеу
элементтері бар есептер жатады. Бұған берілген есепті шығарғанда қатені
табу, есепті бірнеше жолмен шығару, өздігінен есеп құрастыру және т.с.с.
Есеп шығару барысында шығармашылық қабілеттілік, ізденушілік
қасиеттерді дамытып өрістетуге берілген есепті әртүрлі тәсілмен шығарып,
ішінен ең қарапайым, тиімдісін таңдап алудың маңызы зор. Мұның өзі
оқушылардың біліміндегі формализмді жоюға, ой оралымдылығын тәрбиелеуге
мүмкіндік береді. Есеп шығаруда оқушылардың дербестігін тәрбиелеу,
шығармашылық қабілетін арттыру жолдарының бірі – оларды өздігінен есеп
құруға машықтандыру. Өздігінен есеп құрастыру арқылы оқушы төл логикалық
мүмкіндіктерін пайдаланады, тригонометриялық фактілердің арасында жаңа
байланыстарды ашады.
Қазіргі қоғамда пайдалы еңбек еткенде қажет болатын және де басқа
пәндерді оқып үйренуге, білімін ары қарай жалғастыруға толық мүмкіншілік
беретін тригонометриялық білім, іскерлік және дағдылардың негізін берік
және саналы түрде меңгеріп алуын қамтамасыз ету, өзінің білімін тереңдетуге
үйрету мәселелеріне айрықша маңыз беріліп отыр. Себебі, мемлекеттік
стандартта, орта білім беретін мектептерде әрбір шәкіртті жеке тұлға деп
санап, оларды өз сұраныстарына, мүдделеріне сай оқыту мен тәрбиелеудің сан
қилы үлгілерін қолдану керектігі көзделген.
Оқушылардан шығармашылықты талап ететін есептерді қарастыра отырып,
біз олардың білімдерін толықтыруға, сапасын арттыруға мүмкіндік аламыз. Ол
үшін мектеп оқушылары үнемі ізденісте болуы қажет. Сонда ғана болашақта өз-
өзіне сенімді тұлғаларды тәрбиелей аламыз.
Бұл дипломдық жұмыстың басты мақсаты – тригонометриялық
функцияларды жетілдіре оқыту жолдарын көрсету және тригонометриялық
теңдеулерді шешудің тиімді әдістерін айқындау, тұжырымдап шешу әдістемесін
қалыптастыру.

1-тарау. Тригонометриялық функциялардың маңызды
тұстарын жетілдіре оқыту

1.1 Тригонометриялық функцияларды жетілдіре оқыту жолдары

Анықтама. Егер аргумент бір бірінен T периодымен ерекшеленетін бірдей
мәнді қабылдаса, онда функция периодты функция деп аталады.
Сонымен, егер период T анықталғанда мынадай тепе теңдік
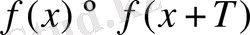орындалса, онда T периодымен 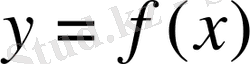функциясы периодты функция деп аталады.
Біз ұзындығы периодқа тең, кесіндідегі периодты функцияның барлық
анықталу облысындағы қасиеттерін білеміз.
1. функциясын зерттеу. функциясы периодты функция, яғни
бұл функция үшін тепе теңдігі орындалады. Бұл функцияның
периоды . функциясы барлық x те анықталады яғни: .
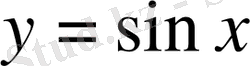функциясы графигінің Ox өсімен қиылысу нүктелерін анықтау үшін
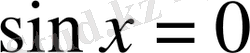теңдеуін шешеміз яғни: 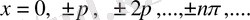. 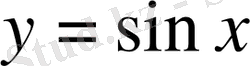функциясының графигі
координаталар басынан өтеді.
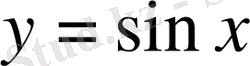функциясы тақ, яғни 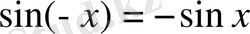сондықтан, оның графигі координаталар
басына қатысты симметриялы.
Тригонометриядан белгілі, егер х бұрышы бірінші 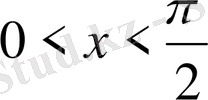немесе төртінші
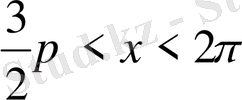ширектерде орналасса, онда 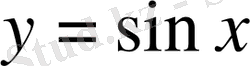функциясы өседі, ал екінші немесе
үшінші 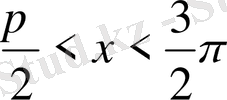ширектерде орналасса онда, функция кемиді. Сондықтан,
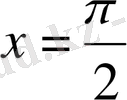нүктесі максимум нүкте, ал 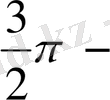нүктесі минимум нүкте деп аталады.
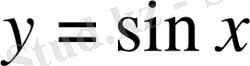периодты функция, онда максимум 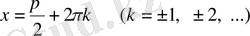нүктесі, ал минимум нүктесі
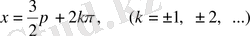болады.
Функция графигін ойыс және дөңестікке зерттеу. Ол үшін айырманың
таңбасын анықтаймыз :

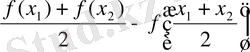Көбейткіш 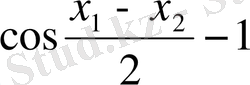кейде теріс, кейде нөлге тең екенін байқаймыз, яғни
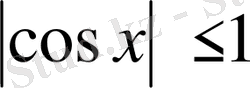. Егер 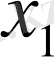және 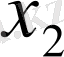бұрыштары бір ширекте орналасса, онда олардың
қосындысы да 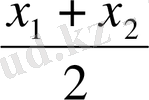сол ширекте орналасады, яғни

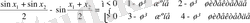
Бірінші және екінші ширектерде яғни 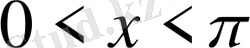болғанда график дөңес, ал
үшінші және төртінші ширектерде яғни 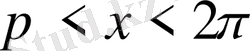болғанда график ойыс болады.
нүктесі функция графигінің иілу нүктесі деп аталады.
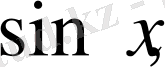функциясының периодтылығын ескерсек, онда 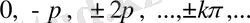нүктелері де функция
графигінің иілу нүктелері екенін көрсетуге болады.
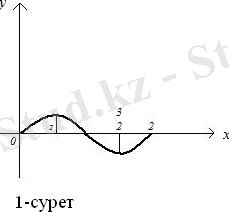
Алынған мәліметтерді пайдаланып, 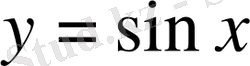функциясының графигін
тұрғызамыз. Бұл график синусоида деп аталады (1-сурет).

Шектелген функциялар ұғымы. Егер функцияның барлық мәндерінде оның
абсолюттік шамасы қандай да бір оң саннан асып кетпесе, яғни

онда 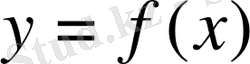функциясы шектелген функция деп аталады.
функциясы шектелген, яғни
.
2. функциясын зерттеу. Бұл функция графигінің Ох өсімен қиылысу
нүктелерін табамыз. деп алсақ, онда мынаны 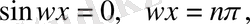немесе
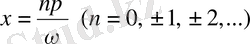аламыз. Мысалы, 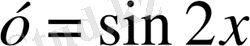болсын. Онда 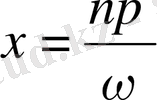болады, ал 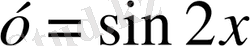функциясының
графигі Ох өсімен қиылысу нүктелерінің аралығы, сәйкесінше
функциясының графигінен екі есе кіші болады. (көршілес нүктелердің аралығы)
(2-сурет). Функцияның периоды да өзгереді. Егер 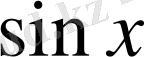тің периоды
болса онда 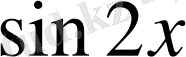тің периоды екі рет кішірейеді, яғни: ге тең.

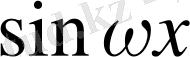функциясының Т периоды 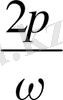ге тең, яғни х және
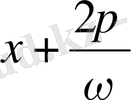нүктелерінде 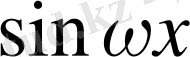функциясы бір мәнді қабылдайды. Шынында да,

яғни
.
функциясының максимум нүктесі 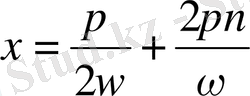, ал минимум нүктесі .
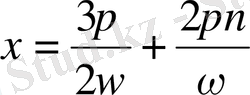Осындай талқылаудан кейін мынадай қорытынды жасауға болады, яғни
функциясының графигі Ох өсінде функциясының графигі 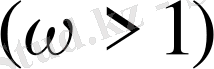болғанда
сығылғаннан алынуы немесе 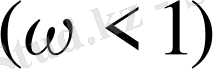болғанда созылуы мүмкін. 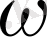коэффициенті
жиілік деп аталады. Периодтың жиілікке байланысты қатынасы көрсетілген
.
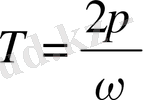Енді 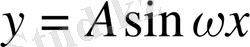функциясын қарастырайық, мысалы 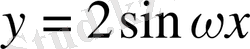болсын. Бұл функция
графигінің қиылысу нүктесі функциясының графигіндегідей болады, бірақ
функцияның максимум және минимум нүктелердегі мәні абсолюттік шамасы
бойынша екі есе ұлғаяды (3-сурет). Ал, А коэффициенті Оу өсінде қисықты
сығады немесе созады. Бұл коэффициент Ох өсінен қисықтың максимальды
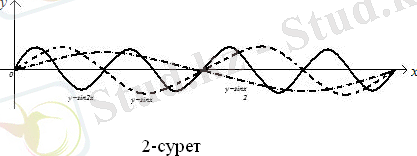
ауытқуын анықтайтын амплитуда деп аталады. болғанда
функциясының графигі 4-суретте көрсетілген.

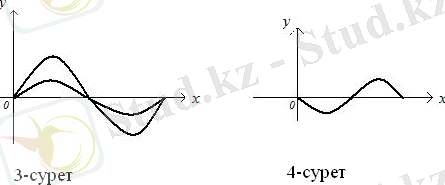
3. Қарапайым гармониялық тербелістің теңдеуі. Қарапайым гармониялық
тербелістің теңдеуі

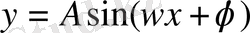
теңдеуімен анықталады. Бұл теңдеуге түрлендірулер жасаймыз, яғни: .
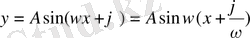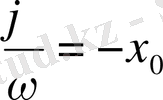белгілеуін енгізсек, онда теңдеу мына түрде 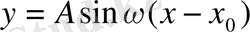болады. Бұдан
көрініп тұрғандай, 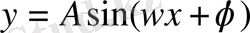қисығы Ох өсінің 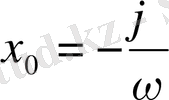нүктесінде 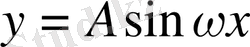қисығына
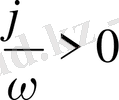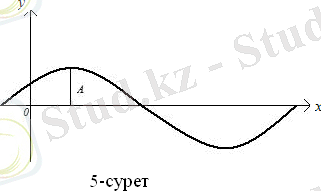
қарағанда сығылады. Егер , онда солға, ал 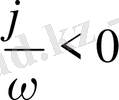болса, онда оңға
жылжиды. (5-сурет). коэффициенті бастапқы фаза деп аталады.

Сонымен,

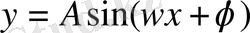
теңдеудегі коэффициенттер: А – амплитуда, 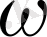- жиілік, – бастапқы
фаза.
4. 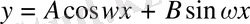функциясын қарапайым гармониялық тербелістің түріне келтіру.
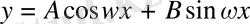теңдеуін қарастырамыз және оны мына түрдегі 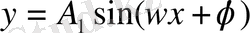қарапайым
гармониялық тербелістің теңдеуімен теңестіреміз,
.
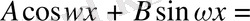
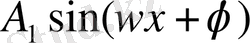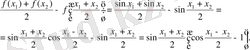
Бұл теңдіктің оң жағын 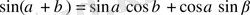формуласы бойынша ашып жазамыз. Сонда
алатынымыз:
.
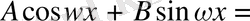
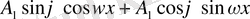Теңдіктің оң және сол жақтарындағы сәйкесінш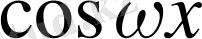е және 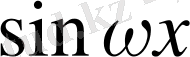тің
коэффициенттерін теңестіреміз
.
Мұндай теңестіруді орындағаннан кейін 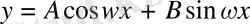теңдеуі қарапайым
гармониялық тербелістің теңдеуімен сәйкес келеді
.
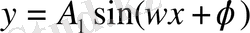Енді, егер А және В белгісіз болса, онда 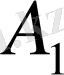амплитуданы және
бастапқы фазаны қалай табу керектігін қарастырамыз. Ол үшін бұл
теңдіктерін квадраттап және оларды қосамыз. Сонда 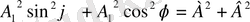немесе 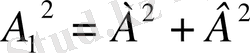онда
.
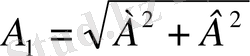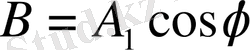теңдігінен 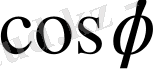ді табамыз
,
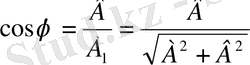бұдан
.
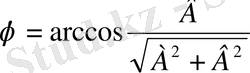Мысал. 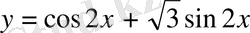функциясын қарапайым гармониялық тербеліс түріне келтіру
керек.
Амплитуда 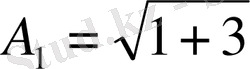, бастапқы фаза 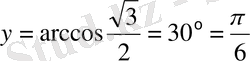, ал жиілігі ге тең.
Онда теңдеу мынадай

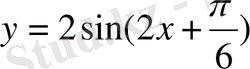
түрге келеді. Бұл функцияның периоды 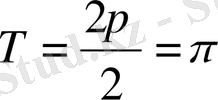ге тең. Функцияның графигі
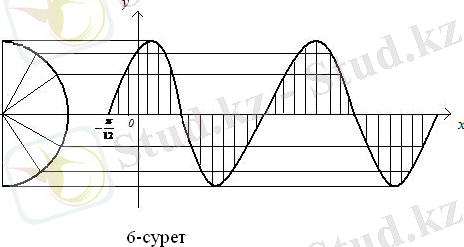
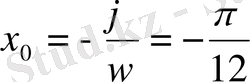нүктесіне жылжиды (6-сурет).

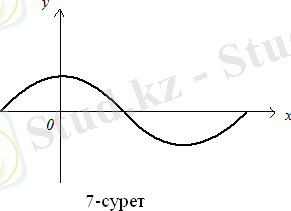
5. Тригонометриялық функцияларға тәуелді өрнектелетін мысалдар. а)
Егер жіңішке тік бұрышты стерженьге Ох өсінде сығатын күш әсер етсе, онда
стержень деформацияланады. Күш белгілі бір мәнге жеткенде стержень иіледі
және синусоид толқынының жарты формасын қабылдайды. (7-сурет)

б) Айнымалы ток тізбегі ток күшінен тәуелді және 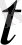уақытының
формуласымен өрнектеледі
.
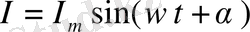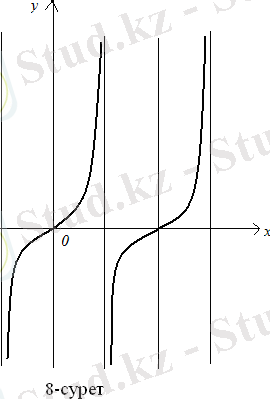
Бұл тәуелділіктің графигі координаталар басынан 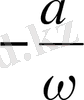шамасына
жылжитын синусоиданы бейнелейді. (8-сурет).

1.2 Кері тригонометриялық функциялардың маңызды
тұстарын жетілдіре оқыту

Функциялық тәуелділік х және у шамаларының арасындағы 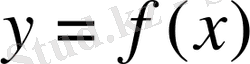теңдеуімен
берілсін. Егер бұл теңдеудегі х және у тің орнын ауыстырсақ, онда кері
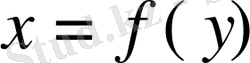деп аталатын функциялық тәуелділікті аламыз. Бұл тәуелділікті
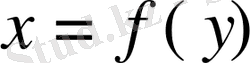теңдеуін у ке қатысты шешеміз. Онда 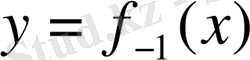екенін аламыз. 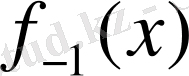функциясы
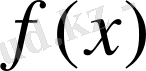функциясына кері деп аталады. Берілген кері функцияны табу үшін
теңдеудегі х және у тің орындарын ауыстырып, алынған теңдеуді у ке қатысты
анықтаймыз.
Мысал 1. 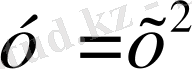функциясы берілсін.
х және у тің орындарын ауыстырып, алатынымыз 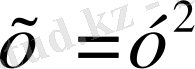. Бұл теңдеуді у ке
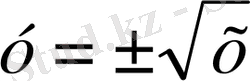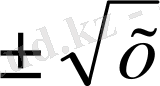
қатысты шешеміз: . Сонда, 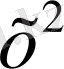функциясына кері функция деп
аталады.
Мысал 2. 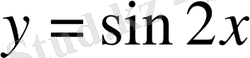функциясы берілсін. х және у тің орындарын ауыстырамыз,
сонда 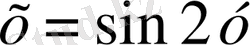аламыз. Бұдан 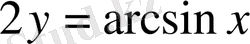, немес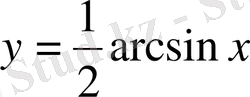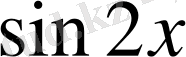е . және функциялары
өзара – кері функциялар.
2. Кері функцияның графигі. Координаталар өсіндегі мәнін өзгертпей
сәйкесінше теңдеудегі х және у тің орындарын ауыстырамыз. Берілген
функцияның графигі 9-суреттегідей болады. Ал оған кері функцияның графигі
10-суретте көрсетілген.
Координаталар өсін әдеттегідей жағдайға келтіру үшін бірінші және
үшінші координаттық бұрыш биссектрисасын хОу жазықтығында градусқа
бұрамыз.

Онда график 11-суреттегідей болады. Егер 9 – және 11 – суреттерді бір
графикке орналастырсақ, онда 12-суреттегідей кері функцияның графиктері
бірінші және үшінші координаттық бұрыш биссектрисасына қатысты және түзуге
симметриялы орналасады. функцияның графигіндегі мысалға қайта
ораламыз, Оу өсіне қатысты симметриялы төбесі координаталар басында жататын
парабола деп аталады.

Кері функцияның графигі де төбесі координаталар басында жататын,
бірақ Ох өсіне қатысты симметриялы болатын парабола (13-сурет).

3. Кері функцияның қасиеті. Қандай да бір өзара кері функцияның
графигінің симметриялық қасиетін қарастырамыз.
1) Ох өсімен қиылысатын кері функцияның графигі Оу өсімен қиылысатын
нүктеден де өтеді.
2) Егер функция өссе (кемісе), онда кері функция да өседі (кемиді) (14-
сурет).
3) Функцияның минимумы (максимумы) болсын. Бұл функцияның графигі екі
нүктеде, түзуімен қиылысады және Ох өсіне параллель, онда кері
функцияның графигі де сәйкесінше түзуімен екі нүктеде қиылысады және
Оу өсіне параллель, онда х тің әрбір мәнінде сәйкесінше у тің екі мәні
болады. Кері функция екі мәнді (15-сурет).

Сонымен, егер функцияның минимумы немесе максимумы болса, онда кері
функция көпмәнді.
4) Егер функцияның графигі ойыс болса, онда кері функцияның графигі
ойыс та, дөңес те болуы мүмкін (16-сурет).

Егер функция кемісе, онда оның графигінде ойыстық немесе дөңестік
қасиеттері кері функцияға өткенде сақталады. Егер де функция өссе, онда
олардың қасиеттері қарама қарсыға ауысады.

5) Егер кері функцияның графигінде тік асимптота болса, онда көлденең
асимптотасы да болады.
4. Логарифмдік функция . және функциялары өзара кері
функциялар. қасиеттеріне сүйене отырып, функциясының қасиетін
қарастырамыз. Сондай ақ, функциясының графигі нүктесінде Оу
өсімен қиылысады. Онда функциясының графигі нүктесінде Ох
өсімен қиылысады. функциясы болғанда өседі, оның графигі ойыс
және түзуі көлденең асимптота болады. Ал, оған кері функция өседі,
оның графигі дөңес және түзуі тік асимптота болады.
5. Кері тригонометриялық функциялар және олардың негізгі мәндері.
болса, онда оған кері функция .
функциясын зерттеген едік. Оның графигі Ох өсімен
нүктелерде қиылысады, нүктеде максимум ал нүктеде минимумы
болады, ол және екі түзуімен шектеледі (19-сурет).

Ал, кері функциясының графигі нүктеде Оу өсімен қиылысады.
Бұл кері функция көпмәнді: әрбір х тің мәнінде функция сәйкесінше шексіз
көп мәнге ие. (Оу өсіне параллель және осы түзумен қиылысады).
функциясының графигі және түзулерімен шектелген (20-сурет).
көпмәнді функциясының графигінен қандай да бір бірмәнді
функцияны бөліп алуға болады. Координаталар басына жақын орналасқан
графиктің барлық бөлігін алу ыңғайлы (21-сурет). Осы жолмен алынған
функцияны арксинустың негізгі мәні деп атап,

деп белгілейміз. және мәндермен шектелген функция
болғанда анықталады:
.
болса, онда (22-сурет) (23-сурет).

функциясының графигі Оу өсімен нүктесінде, ал Ох өсімен
нүктесінде қиылысады және нүктелерде максимум, нүктелерде
минимумы болады.
Бірінші және үшінші координаттық бұрыш биссектрисасына қатысты
симметриялы графигінен, кері функциясының графигін аламыз. Кері
функциясының графигі Ох өсімен нүктесінде, ал ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.