Геометриялық салу құралдары

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 50 бет
Таңдаулыға:

Мазмұны:

Кiрiспе
1 тарау. Геометриялық салулар теориясының кейбiр мәселелерi
1. Конструктивтi геометрияның негiзгi ұғымдары мен аксиомалары
2. Геометриялық салу құралдары
3. Салу есептерi
4. Қарапайым геометриялық салулар
5. Салу есептерiн шешу әдiстемесi
6. Салу есептерiне мысалдар
2 тарау. Салу есептерiн шешу әдiстерi
§1. НГО әдiсi
1.1 НГО ұғымы
1.2 Қарапайым НГО
1.3 НГО iздеу
1.4 НГО әдiсiмен шешiлетiн геометриялық салуларға мысалдар
§2. Түрлендiрулер әдiсi
2.1 Параллель көшiру әдiсi
2.2 Осьтiк симметрия әдiсi
2.3 Центрлiк симметрия әдiсi
2.4 Бұру әдiсi
2.5 Ұқсас түрлендiру әдiсi
2.6 Түрлендiрулер әдiсiмен шешiлетiн геометриялық салуларға
мысалдар
§3. Алгебралық әдiс
3.1 Карапайым формулалармен берiлген негiзгi кесіндiлердi салу
3.2 Квадрат теңдеудiң түбiрлерiн тұрғызу
3.3 Тригонометриялык түрде өрнектелген кесiндiнi салу
3.4 Алгебралық әдiс бойынша шешiлетiн салу есептерiне мысалдар
§4. Инверсия әдiсi
4.1 Инверсияның анықтамасы, қарапайым қасиеттерi
4.2 Инверсияда нүктенiң образын тұрғызу
4.3 Салу есептерiн инверсия әдiсiмен шешу барысында
қолданылатын
теоремалар
4.4 Аполлоний есебi
4.5 Инверсия әдiсiмен шешiлетiн салу есептерiне мысалдар
Пайдаланылған әдебиеттер

Кіріспе

Геометриялық салуларға б.э.д. VI - V ғасырларда ежелгi грек
математиктерi ерекше назар аударған. Пифагор (б.э.д.VI ғ) және оның
шәкiрттерi, Гиппократ (б.э.д. V ғ), Евклид, Архимед, Аполлоний (б.э.д. III
ғ), ежелгi отырарлық Әл-Фараби (870 – 950 ж.ж.) геометрияның осы
саласына өз үлестерiн қосып, оны дамытты.
Пифагор мектебiнiң математиктерi дұрыс бесбұрыш салу сияқты
күрделi есептердi шеше бiлдi. Б.э.д. V ғасырда дөңгелектiң
квадратурасы, кубты екi еселеу, бұрыштың трисекциясы секiлдi атақты
есептер пайда болды. Циркуль мен сызғыштың көмегiмен салынбайтыны белгiлi
болған бұл есептер көптеген ғасырлар бойы зерттеушiлердiң назарында
болған.
Геометрияның және математиканың кейбiр басқа салаларының тарихы
геометриялық салулар теориясының дамуымен тығыз байланысты болды.
Б.э.д. 300 жылдары құрылған Евклид геометриясының кез-келген нүктеден кез-
келген нүктеге дейiн түзу сызық жүргiзуге болады, шектелген түзудi
керегiнше (шексiз) созуға болады, кез–келген центрден кез–келген
өлшеммен шеңбер сызуға болады т.б. аксиомалары геометрияның кұрылуында
салулардың ролi қаншалықты маңызды болғандығын көрсетедi.
Геометриялық салулар ІХ – ХV ғасырларда Араб және Таяу Шығыс
елдеріндегі ұлы математиктердің де назарында болды. Әл – Фарабидің Табиғат
сырын геометриялық фигуралар арқылы танытарлық рухани айла әрекеттері деп
аталатын шығармасы түгелдей геометрия мәселелеріне арналып, 150 – ге тарта
салу есептері шығарылған. Он бес есеп сызғыш пен адымы тұрақты циркуль
арқылы шешіледі. Әл – Фарабидің негізгі жетістігі - әр жерде шашырап
жүрген геометриялық салу есептері туралы материалдарды жинастырып, жүйеге
келтірген принциптер тағайындады және геометрияның белгілі бір саласына
айналдырды.
ХVІ ғасырда салу есептерін шешумен ұлы суретші ғалым Леонардо да
Винчи (1452 – 1519) айналысқан. Оның салуларында, тіпті Әл – Фарабимен дәл
келетін жерлері бар. Әл–Фараби, Әбу әл Вафа, Леонардо да Винчи, т. б.
ғалымдардан басталған геометриялық салу есептерін жүйелеу әрекеттері
XVIIІ – XІX ғасырларда белгілі математиктер Э. Маскерони, Я. Штейнер
еңбектерінде өз жалғасын тауып, қазіргі конструктивтік геометрияның
қалыптасуына бастама болды.
Дегенмен, ортағасырларда конструктивтi геометрия мәселелерiмен
көптеген математиктер еңбектенсе де, бұл салада айтарлықтай өзгерiстер
болмады. Тек XVII-XX ғ.ғ. математиканың жаңа салаларының өркендеуiне
байланысты геометриялық салулар теориясы дами бастады. Бiр жағынан,
конструктивтi геометрияның мәселелерi жаңа математикалық теориялар
мен әдiстердiң өркендеуiне ыкпалын тигiздi. Әсiресе геометриялық
салулармен тығыз байланыста дамығандар: аналетикалық геометрия, проективтiк
геометрия, алгебралық және трансценденттiк сандар теориясы,
аналетикалық функциялар теорясы және т.б.
Р.Декарт (1596-1650), Ньютон (1643-1727), Эйлер (1707-1783), Гаусс
(1744-1808), Ферма, т.б. математиктер конструктивтi есептермен шұ-
ғылданған. Мәселен, Декарт және Ньютон конустық қиманың көмегiмен
бұрыштың трисекциясы туралы есептi шешсе, Ньютон мен Эйлер Аполлоний
есебiн шешудiң өз әдiстерiн жасады. XVIIІ – XІX ғасырларда белгілі матема-
тиктер Э.Маскерони, Я.Штейнер еңбектері қазіргі конструктивтік геометрия-
ның қалыптасуына бастама болды.
XIX - XX ғасырларда геометриялық салулар теориясында көптеген
еңбектер жазылды. Ф.Клейн мен Энриквестiң Геометриялық салулар теориясы
кiтабы, Лебег пен Бибербаханың, А.Адлердiң еңбектерi жарияланды. 1881 жылы
жарыққа шыққан И.И.Александровтың Гео-метриялық салу есептерiн шешу
әдiстерi атты кiтабы ең үздiк туындылардың бiрi болды. Геометриялық
салулар теориясының дамуы физикадағы, сызудағы кейбiр мәселелердi шешуге
көмектестi. Мысалы, физикалық шамалардың өзгерiсiн графиктiк жолмен
сипаттауда, геометриялық фигуралардың сызбаларын орындауда қолданылды.
Инженерлер мен техниктер кейбір практикалық жұмыстарды графиктер мен
сызбалардың көмегімен орындады.
Математиканы оқытуда салу есептерiне аса көңiл бөлiнедi, себебi
ондай есептер мазмұны жағынан да, құрылымы жағынан да оқушыларға
түсiнiктi. Бұл - нағыз шағын математикалық зерттеу. Геометриялық салулар
оқушының математикалық белсенділігін, кеңiстiкті елестету тапқырлығы мен
алғырлығының дамуына, яғни болашақ маман иесiне қажет қасиеттердiң
дамуына әсер етедi. Салу есептерiн шешу барысында кескіндеу
сауаттылығының теориялық және практикалық негiздерi қалыптасады, яғни
оқушы есептi шешудiң жиi қолданылатын әдiстерi мен әртүрлi шарттарға
сәйкес қолданылатын құрал - жабдықтармен танысады. Бұл, әдетте, есептi
формальды қабылдауға жол бермейдi. Мектептегі геометрия курсының әрбір
тарауының соңында салу есептерін шешу оқушыларды осы тақырыпты терең
меңгеруіне әсер етеді.

1 тарау. Геометриялық салулар теориясының
кейбiр мәселелерi
1. Конструктивтi геометрияның негiзгi ұғымдары мен аксиомалары
Геометриялық салуларды оқытатын геометрияның бөлiмi конструктивтi
геометрия деп аталады. Конструктивтi геометрияның негiзгi ұғымы
геометриялық фигураны салу болып табылады. Бұл ұғым анықтамасыз
қабылданады. Оның нақты мағынасы практикада жиi қолданылатын сызу
(сызықты), жүргiзу (шеңбер немесе түзуді), көрсету (нүктенi) және т.б.
сөздерiнiң мағынасымен пара - пар.
Конструктивтi геометрияның негiзгi талаптары (постулаттар) сызба
жұмысының ең басты кезеңдерiн абстрактылы түрде бейнелейдi. Олар дәлелсiз
қабылданған аксиомалар болып табылады және конструктивтi геометрияны
логикалық негiздеуде қолданылады. Постулаттарды салу қадамдары деп те
атайды. Олар мыналар:
П1. Тұрғызылған екі нүкте арқылы түзу салу.
П2. Берілген нүктені центр етіп алып, берілген радиуспен шеңбер салу.
П3. Тұрғызылған параллель емес екі түзудің қиылысу нүктесін салу
П4. Егер тұрғызылған шеңбер мен түзу қиылысатын болса, олардың қиылысу
нүктесін салу.
П5. Егер тұрғызылған екі шеңбер қиылысса, олардың қиылысу нүктесін салу.
Ендi геометриялық салулар теориясының аксиомаларын қарастырайық:
I. Қандай да бiр фигура берiлген болса, онда ол салынған
(тұрғызылған) деп есептелiнедi.
II. Егер екі (немесе одан да көп) фигура салынса , онда осы
фигуралардың бiрiгуi де салынған болып есептеледi.
III. Егер екi фигура салынса, онда олардың айырмасы кұр жиын болу-
болмауын аныңтауға болады
IV. Егер салынған екi фигураның айырмасы кұр жиын болмаса, онда бұл
айырма да салынған.
V. Егер екi фигура салынса, онда олардың қимасы кұр жиын болатын
-болмайтынын анықтауға болады.
VI. Егер салынған екi фигураның қимасы кұр жиын болмаса, онда бұл қима да
салынған болып есептеледi.
VII. Тұрғызылған екi фигураның кез-келген саны шектi ортақ нүктелерiн салу-
ға болады, егер олар бар болса.
VIII. Тұрғызылған фигураға тиiстi нүктенi салуға болады, егер олар бар
болса.
IX. Тұрғызылған фигураға тиiстi емес нүктенi салуға болады.
I - IX аксиомалары конструктивтi геометрияның жалпы аксиомалары деп
аталады.
2. Геометриялық салу кұралдары
Ежелгi грек математиктерi салу есептерiн шешу барысында сызғыш
пен циркульды пайдаланған және шын геометриялық салу деп, осы екі
құралдың көмегімен шешілетін есептерді атады. Евклидтің постулаттарына
сәйкес сызғыш шексіз, әрі бір жақты құрал, циркуль кез - келген өлшемді
шеңбер салу құралы делінді. Бұлардан басқа да салу құралдары болған.
Мысалы, Платон б.э.д. 400 жылдар шамасында кубты екі еселеу туралы
есепті екі тікбұрыштың көмегімен шешсе, Архимед бұрыштың трисекциясы
туралы есепті тікбұрышты сызғышты қолданып шешеді. Дәл осы есепті әртүрлі
қисықтардың көмегімен Никомед (конхойданы пайдаланып), Диоклес (циссойданы
пайдаланып), Папп және басқалары шешті.
XVII - XIX ғасырларда геометриялық салу құралдарының жаңа түрлері
ойлап шығарылды. Леонардо да Винчи (1452-1549) сызғыш және тұрақты ашалы
циркульдың көмегімен шешілетін есептерді, Датчани Мор (1672) мен итальяндық
Маскерони (1779) тек қана сызғыш пен циркульды қолданып шешілетін
салуларды зерттеген және олардың ішінде тек циркульмен шешілетіндерін
тапқан. Осындай зерттеулердің негізінде салу есептерінде екі жақты сызғыш,
тікбұрыш сияқты құралдар қолданыла бастады. Бірақ конструктивтік
геометрияның ең негізгі құралдарына бір жақты сызғыш пен циркуль
жатады және оларды классикалық құралдар деп атайды, ал қалғандары қосымша
құралдар болып саналады.
Конструктивті геометрия үшін қолданылатын құралдардың дәл сипат-
тамасы көрсетілуі керек. Мұндай сипаттамалар аксиомалар түрінде беріледі.
А. Сызғыш аксиомасы
Сызғышпен келесі геометриялық салулар орындалады:
1) тұрғызылған екі нүктені қосатын кесінді салу;
2) салынған екі нүкте арқылы түзу жүргізу;
3) салынған нүктеден бастап екінші салынған нүкте арқылы өтетін сәуле
жүргізу.
В. Циркуль аксиомасы
Циркульдың көмегімен мына геометриялық салулар орындалады:
1) берілген центрі мен радиусқа тең кесіндісі (немесе кесіндінің ұштары)
бойынша шеңбер салу;
2) берілген центрі мен кез - келген доғасының ұштары бойынша шеңбердің
доғасын салу.
Циркуль мен сызғыштың көмегімен орындалатын негізгі салулар:
1) Берілген екі нүктені қосатын кесіндіні салу (А.1);
2) Берілген екі нүкте арқылы түзу жүргізу (А.2);
3) Берілген нүктеден бастап екінші берілген нүкте арқылы өтетін
сәуле жүргізу (А.3);
4) Берілген центрі мен радиусқа тең кесіндісі (немесе кесіндінің
ұштары) бойынша шеңбер салу (Б.1);
5) Берілген центрі мен кез-келген доғасының ұштары бойынша шеңбердің
екі доғасының кез-келгенін салу (Б.2);
6) Тұрғызылған екі фигураның саны шекті ортақ нүктелерін салу, егер
олар бар болса (акс.VII);
7) Қандай да бір тұрғызылған фигураға тиісті нүкте салу (акс.VIII);
8) Қандай да бір тұрғызылған фигураға тиісті емес нүктені салу
(акс.IX).
3. Салу есептері
Салу есебі деп берілген элеметтері бойынша геометриялық құралдардың
(сызғыш және циркуль) көмегімен белгілі бір шарттарды қанағаттандыратын
геометриялық фигураны салуды айтады. Ондай есептерді шешудің белгілі бір
алгоритмі жоқ. Cалу есебін шешу ізделінді фигураны қалай салуға болатынын
талдаудан басталады. Есеп шешілді деп санау үшін фигураны салу тәсілі
көрсетіліп, салу жұмыстарын орындау нәтижесінде шынында да ізделінді фигура
салынғандығын дәлелдеу керек. Сонымен, салу есебінің шешімі деп, берілген
шартты қанағаттандыратын әрбір фигураны айтады. Салу есебінің шешімін табу
деп оны саны шектеулі негізгі салуларға келтіруді, яғни ретімен
орындағанда ізделінді фигура конструктивті геометрияның аксиомаларының
негізінде салынды деп есептелінетіндей негізгі салулардың шекті тізбегін
көрсетуді айтады. Негізгі салулар тізбегі қандай құралдарды пайдалану
керектігіне байланысты.
Салу есебінің барлық шешімдерін табу оны шешу деп аталады. Салу
есебі жалпы түрде келесідей тұжырымдалады: салынған (негізгі) Ғ1, Ғ2 , ...
,Ғк фигураларының жиыны берілген және ізделінді Ф фигурасын сипаттайтын
қасиеттер көрсетілген. П1 – П5 постулаттарын қолданып, салынған және
ізделінді фигураларды қамтитын шекті жиын табу керек.
Есеп шартын қанағаттандыратын фигура формасы және жазықтықта
орналасуы бойынша ажыратылады. Фигураның жазықтықта орналасуын ескеру -
ескермеу есептің құрылысына байланысты.
1) Егер есепте ізделінді фигураның берілген фигураға қатысты орналасуы
қарастырылмаса, онда тек есеп шартын қанағаттандыратын өзара тең емес
барлық фигураларды тауып көрсетеміз. Онда салу есебі шешілген деп
есептелінеді, егер
- есеп шартын қанағаттандыратын өзара тең емес кейбір Ф1, Ф2, ..., Фn
фигуралары салынса,
- есеп шартын қанағаттандыратын кез - келген фигура осы фигуралардың
біріне тең болатыны дәлелденсе.
Бұл жағдайда есептің әр түрлі n шешуі бар делінеді.
2) Егер есептің шартында ізделінді фигураның берілген фигураға
қатысты нақты орналасуы көрсетілсе, онда толық шешу берілген шартты
қанағаттандыратын барлық фигураларды салу болып табылады (егер мұндай
фигуралардың саны шекті болса). Сондай-ақ мұнда берілген фигураға қатысты
әр түрлі қалыпта орналасқан тең фигуралар есептің әр түрлі шешулері
болып саналады.
Кейде есеп шартын қанағаттандыратындай фигура болмауы мүмкін.
Мысалы, берілген тіктөртбұрыш квадрат болмаса, оған іштей шеңбер сыза
алмаймыз немесе концентрлі екі шеңберге ортақ жанама жүргізілмейді.
Кейде есептің шешімі бар, бірақ ол берілген құралдардың көмегімен
салынбауы мүмкін. Онда салу есебін шешу деп ізделінді фигура берілген
құралдардың көмегімен салынбайтындығын дәлелдеп көрсетуді айтады.
4. Қарапайым геометриялық салулар
Қарапайым есептердің шешулерін негізгі салуларға келтіру үшін де
көптеген логикалық қадамдар жасауға тура келеді. Ал қиынырақ есептерді
шешудің логикалық структурасын тұрғызу одан да қиынға соғады. Сондықтан
күрделі есептерде қарапайым салу есептерін біле отырып, салу қадамдарын
үнемдеуімізге болады, яғни қарапайым салуларды болашақта негізгі салуларға
келтірмей - ақ қолдана аламыз.
Күрделі есептердің бөлігі ретінде жиі кездесетін қарапайым
геометриялық салулар мектеп курсының бірінші Оларға мыналар жатады:
1) Берілген кесіндіні қақ бөлу
2) Берілген бұрышты қақ бөлу (бұрыш биссектрисасын салу)
3) Берілген кесіндіге тең кесінді салу
4) Берілген бұрышқа тең бұрыш салу
5) Берілген түзуге одан тысқары нүкте арқылы параллель түзу жүргізу
6) Берілген түзуге одан тысқары жатқан берілген нүкте арқылы перпен-
дикуляр тұрғызу.
7) Берілген кесіндіні берілген қатынаста бөлу
8) Берілген үш қабырғасы бойынша үшбұрыш салу
9) Берілген қабырғасы мен сол қабырғаға іргелес екі бұрышы бойынша
үшбұрыш салу
10) Берілген екі қабырғасы және олардың арасындағы бұрышы бойынша үшбұрыш
салу
11) Берілген шеңберге берілген нүкте арқылы жанама жүргізу
12) Берілген гипотенузасы мен катеті бойынша тікбұрышты үшбұрыш салу
5. Салу есептерін шешу әдістемесі
Конструктивті есептерді шешудің схемасын таңдау әдістемелік сұрақ
болып табылады. Геометриялық салу есептерін шешу төмендегі схема бойынша
жүргізілгенде ғана дұрыс деп саналады:
1) Берілгендерді таңдауда барлық мүмкіндіктерді қамтитын
жағдайлардың ақырлы саны белгіленеді;
2) Әрбір жағдай үшін есептің шешуі болу - болмауы және шешімі
болса, олардың саны анықталады;
3) Әрбір жағдай үшін есептің шешімі болса, көрсетілген геометриялық
құралдардың көмегімен оларды салу тәсілдері беріледі немесе оның берілген
құралдармен салынбайтындығы көрсетіледі.
Күрделі есептерде оны шешудің мүмкін болатын жағдайларын, барлық
шешімдерін, шығарылу тәсілін және т.б. анықтау үшін қалай талдау жасау
керектігі жөнінде сұрақ туады. Сондықтан конструктивті есептер мына
схема бойынша шешіледі:
1. Талдау
2. Салу
3. Дәлелдеу
4. Зерттеу
Әрине, бұл схема міндетті және өзгеріссіз емес, оның кейбір
сатыларын қатаң түрде ажыратып, көрсетілген қалыпта ғана орындау мүмкін
бола бермейді. Алайда конструктивті есептерді шешуде бұл схеманың көмегі
мол. Енді схеманың әр этаптарына жеке тоқталып өтейік:
1.Талдау. Бұл - салу есебін шешудің ең негізгі және әзірлеуші бөлімі,
себебі есепті шешудің кілті осында. Талдаудың мақсаты – есептің ізделінді
элементтері мен берілгендері арасындағы байланысты тағайындау арқылы оның
шешу тәсілдерін іздестіру. Оған берілген мен ізделінді фигураларды есеп
шартында көрсетілгендей қалыпта орналастыратын көмекші сызба арқылы қол
жеткіземіз. Бұл сызбаны қолдан сызуға болады. Әдетте, талдау жасау
есеп шешілді делік деген сөздермен басталады. Көмекші сызбаны, негізінен,
берілгендерден емес, ізделінді фигуралардан бастап салған дұрыс. Мысалы,
бір төбесінен жүргізілген медиана, биссектриса және биіктігі бойынша
үшбұрыш салу керек болса, алдымен кез - келген үшбұрыш сызып, содан
соң оның есеп шартында көрсетілген сызықтарын жүргізген ыңғайлы. Егер
көмекші сызбадан ізделінді фигураны салудың тәсілдері анық көрінбесе, онда
ізделіндінің бөлігін немесе оны тұрғызу кезінде қолданылатын қандай да
бір фигураны табамыз.
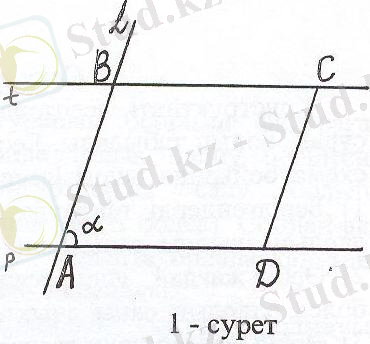
2.Салу. Бұл бөлімде нәтижесінде ізделінді фигура шығатындай негізгі салу-
лар (немесе бұрын шешілген, шығарылған есептер) тізімі беріледі. Салудың
әрбір қадамы көрсетілген құралдың көмегімен графикалық көркемделіп
отырылады. Мысалы, көршілес екі қабырғасы және олардың арасындағы
бұрышы бойынша параллелограмм салу есебінің салу жоспары төмендегіше
болады (1-сурет):
1) кез - келген р түзуі
2) АD(р кесіндісі
3) (DАL(( бұрышы ((-берілген)
4) АВ(АL кесіндісі (берілген қабырға)
5) В нүктесі арқылы t р түзуі
6) ВС(АD, ВС(t кесіндісі
7) С, D нүктелерін қосамыз
АВСD-ізделінді параллелограмм.
3.Дәлелдеу. Дәлелдеудің мақсаты – салынған фигура шынымен де есеп шартын
қанағаттандыратынын көрсету. Салудың әр қадамының орындала-тындығын
дәлелдеу, әдетте, сөйлем түрінде беріледі. Дәлелдеуде мынаны ескеру
керек: талдаудан шығатын салдар дәлелдеудің шарты болып табылады және,
керісінше, талдаудың шарты дәлелдеудің салдары болады.
4.Зерттеу. Салу есептің қандайда бір жалғыз шешімін тұрғызумен
шектеледі және ондағы барлық қадамдар орындалады деп есептелінеді. Ал
есептің толық шешуін табу үшін мына сұрақтарға жауап беру керек:
1) берілген фигуралардың кез-келген орналасуында салу жоспары орындала ма(
2) егер таңдалған салу әдісін басқа жағдайлар үшін қолдануға болмаса,
ізделінді фигура қалай тұрғызылады(
3) берілген фигуралардың әртүрлі орналасуында есептің мүмкін болатын
шешулерінің саны қанша(
Осы сұрақтардың әрқайсысына жауап беру есепті зерттеу болып саналады.
Демек зерттеудің мақсаты – есептің шешілу шартын анықтап, оның
шешімдерінің санын табу.
Зерттеу, негізінен, салу бойынша, салу барысында сөздерімен
басталады. Бұлай қабылдаудың негізгі мақсаты – салудағы әр қадамға
тоқталып, ондағы іс - әрекеттердің әрдайым орындалу - орындалмауын тексеру,
егер орындалса, неше әдіспен екендігін анықтау.
Есепті осылайша талқылаудың нәтижесінде берілген тәсілмен ізделінді
фигураны салу мүмкіндігі белгілі болады. Бұл жерде егер салудың қандай
да бір тәсілін өзгертсе, есептің жаңа шешулері пайда болмай ма( деген
сұрақ туады. Кейде есептің әрбір шешуі оның бұрын анықталған шешуімен
сәйкес келетінін дәлелдеуге болады. Онда зерттеуді ары қарай жүргізіп қажет
емес. Ал егер сәйкес келмейтіндігі дәлелденсе, онда басқа әдіспен
анықталатын
шешулер болуы мүмкін болғандықтан, талдауға қайта оралып, берілген немесе
ізделінді фигуралардың орналасуының басқа жағдайлары қарастырылады. Ал есеп
айтарлықтай жеңіл болғанда, кейбір сатылар, мысалы талдау немесе зерттеу
қарастырылмайды.
6. Салу есептеріне мысалдар
Есеп1: Бір төбесінен жүргізілген биссектрисасы, медианасы және
биіктігі бойынша үшбұрыш салыңыз.
Шешуі:
Талдау: Есеп шешілді делік, АВС – ізделінді үшбұрыш (2-сурет), АН – оның
биіктігі, АМ – медианасы, АD – биссектрисасы.
АВС үшбұрышына сырттай шеңбер сызылған шеңбердің центрін О деп белгілейік,
онда ОМ түзуі ВС хордасына перпендикуляр болғандықтан, ол осы хордамен
керілетін шеңбердің әрбір екі доғасын тең екіге бөледі. АD биссектрисасы да
( шеңберінің ВАС бұрышы тірелетін дәл осы доғасын тең екіге бөледі. Олай
болса, ОМ түзуі мен АD биссектрисасы сырттай сызылған шеңбердің Р
нүктесінде қиылысады. О нүктесінен АР – ға түсірілген перпендикулярдың
табаны – АР-ның ортасы, яғни S нүктесі болады.
Салу: 1) АD = ва гипотенузасы, АН = hа катеті бойынша АНD үшбұрышы
2) (А, mа) шеңбері
3) (А, mа) ( DН = М нүктесі
4) М(l және l ( DН түзуі
5) l ( АD = Р нүктесі
6) t - АР кесіндісінің орта
перпендикуляры
7) t ( МР = О нүктесі
8) ((О, ОА) шеңбері
9) DК ( ( = В және С нүктелері
АВС – ізделінді үшбұрыш.
Дәлелдеу: Салу бойынша АН кесіндісі АВС үшбұрышының биіктігі болады. М
– ВС қабырғасының ортасы, себебі ол шеңбердің центрінен ВС хордасына
түсірілген перпендикулярдың табаны. Сондықтан АМ – медиана. Р нүктесі
ВРС хордасының ортасы болғандықтан, іштей сызылған ВАР және САР бұрыштары
өзара тең, бұдан АD – ВАС бұрышының биссектрисасы.
Зерттеу: Есептің шешімі болу үшін ma ( вa ( ha қатынасы орындалуы қажет,
себебі үшбұрышта биссектриса медиана мен биіктіктің ортасында орналасады,
не бұл кесінділердің бәрі беттеседі. Егер ma = вa = ha болса, онда есеп
биіктігі (ол әрі медиана, әрі биссектриса) бойынша тең бүйірлі үшбұрыш салу
есебіне келеді. Егер ma ( вa ( hа болса, онда салу жоспарының 1) және 2)
қадамдары бірмәнді орындалады. ma ( ва болғандықтан, (А, mа) ( DН қимасының
М нүктесі табылады. Салу жоспарының 5) қадамындағы Р нүктесі жалғыз, себебі
ол екі түзудің қиылысу нүктесі. Сонымен қатар, АРDН және МР ( DН
болғандықтан, АРМР. Бұл АР хордасының орта перпендикуляры міндетті түрде
МР түзуімен қиылысады дегенді білдіреді және ол нүкте сырттай сызылған
шеңбердің центрі болады. DН түзуі ((А, АР) шеңберімен екі нүктеде
қиылысады, себебі ол шеңбердің ішіндегі D нүктесі арқылы өтеді. Сонда
көрсетілген салу жоспары бойынша шешілген есептің шешімі әрдайым табылады.
Есеп 2: hc, hв биіктіктері және mа медианасы бойынша үшбұрыш
салыңыз.
Шешуі:
Талдау: Айталық, АВС – ізделінді үшбұрыш
(3 - сурет), АD = mа, CH = hc, BL = hв.
АС табанына DF перпендикулярын жүргізсек,
DF = (D–медиананың табаны болғандықтан).
Олай болса, АFD тікбұрышты үшбұрышын
АD = mа гипотенузасы мен DF = катеті
бойынша сала аламыз. Дәл осылайша DК = катеті мен АD гипотенузасы
арқылы АDК тікбұрышты үшбұрышын тұрғызуға болады. Сонда ізделінді
үшбұрыштың ВАС бұрышы анықталады.
Салу: 1) АFD тікбұрышты үшбұрышы (АD = mа, DF =, (DFА=900)
2) АDК тікбұрышты үшбұрышы (АD = mа, DК = , (DFА=900)
3) [FD) сәулесіне FЕ = hв кесіндісі
4) Е нүктесі арқылы l║AF түзуі
5) l ∩ [AК) = В нүктесі
6) ВD түзуі
7) ВD ∩ [AF) = С нүктесі
АВС – ізделінді.
Дәлелдеу: Салу бойынша DF = , онда ЕF = hв . Бұдан DЕ = DF = .
Онда (BED = (DFC = 900 екенін ескерсек, ∆DЕВ = ∆DFС. Олай болса, ВD =
DС, яғни АD – медиана және салу бойынша АD = mа.
В нүктесінен АС табанына ВL перпендикулярын түсірсек, BL = EF = hв. Айталық
СН ( АВ, онда СНВ үшбұрышында DК кесіндісі (КАВ) орта сызық болады.
Ал салу бойынша DК = . Бұдан СН = DК = hс.
Зерттеу: Салу жоспарының 1) және 2) қадамдарындағы АDF, АDК үшбұрыш-тарын
салу
mа ( hв, mа ( hс
теңсіздіктері орындалғанда ғана мүмкін болады. Ал 3) – 7) салу қадамдары
әрқашан орындалады. Олай болса, бір уақытта hв ( 2mа және hс ( 2mа
теңсіздіктері орындалғанда есептің жалғыз шешуі бар. Басқа тәсілмен
шешкенде өзге шешім шығуы мүмкін емес, себебі mа( = mа, hc( = hc, hв( = hв
( ∆АВС = ∆А(В(С(.
Есеп 3: р периметрі мен іргелес (, ( бұрыштары бойынша үшбұрыш салу.
Шешуі:
Талдау: Айталық ВС – ізделінді үшбұрыш (4 - сурет),
АВ + ВС + СА = р
және (ВАС = (, (ВСА = (.
Егер АС табанының созындысына АD = AB,
CE = BC болатындай кесінділер белгілесек,
DE кесіндісінің ұзындығы периметрге тең
болады, яғни DE = p. D, E нүктелерін АВС
үшбұрышының В төбесімен қосамыз.
Сонда DBA және EBC тең бүйірлі үшбұрыш-
тары шығады. Үшбұрыштың сыртқы бұрышының қасиетін ескерсек, (ADB = (ABD =
, (CBE = (CEB = . Демек DEB үшбұрышы бір қабырғасы және оған
іргелес екі бұрышы бойынша белгілі.
Салу: 1) DЕВ үшбұрышы (DE = p, (BDE = , (BED = ).
2) DB кесіндісінің орта перпедикуляры: n1
3) DE ∩ n1 = A нүктесі
4) BЕ кесіндісінің орта перпедикуляры: n2
5) DE ∩ n2 = В нүктесі
6) АВ, СВ кесінділері
∆ АВС – ізделінді.
Дәлелдеу: n1, n2 орта перпендикулярлар болғандықтан, сәйкесінше АВ = AD, BC
= CE. Ал салу бойынша DA + AC + CE = p, бұдан АВ + АС + ВС = р.
Егер n1∩ DB = K, n2 ∩ EB = P десек,
(KAD = 900 - , (PCE = 900 - .
Дәл осылайша, (KAВ = 900 - , (PCВ = 900 -
Сонда
(ВАС = 1800 - (ВАD = 1800 - (KAВ - (KAD = 1800 – 900 + - 900 +
=
(ВСA = 1800 - (BCE = 1800 - (PCB - (PCE = 1800 – 900 + - 900 +
=
Зерттеу: ( + ( ( ( шарты орындалғанда есептің шешімі бар және ол жалғыз
болады. Себебі, қарсы жорып, А(В(С( үшбұрышы да шешім болады десек, (В(А(С(
= (, (В(С(А( = (, А(В( + В(С( + С(А( = р, онда ∆АВС = ∆А(В(С(.
Есеп 4: а, в, с түзулері, р кесіндісі берілген. с – а, в түзулерін
қияды. Ұштары а, в түзулерінде болатын, с - ға параллель және р кесіндісіне
тең кесінді салыңыз.
Шешуі:
Талдау: Есеп шешілді делік, А а, В в, АВ = р, АВ с (5-сурет).
Берілген мен ізделінді фигуралардың арасындағы байланысты анықтау үшін,
кейбір қосымша нүктелер мен сызықтар жүргізу керек.
Айталық с ( в = Р. АМ в сәулесін жүргізсек және АМ ( с = Q деп белгіле-
сек, АВРQ төртбұрышты параллелограмм болғандықтан PQ = AB = p.
Cалу: 1) с ( в = Р нүктесі
2) с түзуінен PQ = p кесіндісі (Qс )

3) QМ в түзуі

4) QM ( a = A нүктесі
5) AN c түзуі
6) AN ( в = В нүктесі
АВ – ізделінді кесінді.
Дәлелдеу: Салу бойынша Аа, Вв, АВ с. Ал АВРQ параллелограмм
бол- ғандықтан, АВ = PQ = p.
Зерттеу: Есеп шарты бойынша в, с түзулері қиылысады, онда Р нүктесі әрдайым
табылады. Ал екінші салу қадамындағы РQ кесіндісі екеу болады, (2.4., 3)
салу). Сонда әрбір Q, Q' нүктелері үшін салу жоспары жеке орын-далады.
Мынадай жағдайлар болу мүмкін:
1) QM ( a, онда QM в Q'M' болғандық-
тан, Q'M' түзуі де а түзуін қияды (6-сурет).
2) QM a
3) QM ( а (беттеседі)
1) жағдай а, в түзулері қиылысқанда ғана
мүмкін. Онда 4) - 6) салу қадамдар Q, Q'
нүктелерінің әрқайсысы үшін бірмәнді
орындалады да, есептің екі шешімі болады.
2) жағдай а в және с түзуінің а, в түзулерінің арасындағы кесіндісі р –
дан өзге болғанда ғана орындалады. Онда QM(a = A нүктесі болмайды да,
есептің шешімі жоқ делінеді.

3) жағдай а в және с түзуінің а, в түзулерінің арасындағы кесіндісі р –
ға тең болғанда орындалады. Онда есептің шексіз көп шешімі бар.
Есеп5: СD биссектрисасы және оның С төбесінен жүргізілген
биіктікпен, медианамен арасындағы бұрыштары берілген. Осы элементтері
бойынша АВС үшбұрышын салыңыз.
Шешуі:
Талдау: Есеп шешілді делік, АВС – ізделінді үшбұрыш (7 – сурет). Мұндағы
НСD, МСD бұрыштары және СD биссектрисасы ұшбұрыштың берілген элементтері.
Онда алдымен СD гипотенузасы мен (НСD бойынша НСD, содан соң СН катеті
мен (МСD + (НСD
бойынша НСМ тікбұрышты үшбұрыштарын
тұрғызуға болады. Егер (-АВС үшбұрышы-
на сырттай сызылған шеңбер десек, оның
СD биссектрисасымен қиылысу нүктесі,
яғни Е нүктесі – АВ хордасының ортасы
болады. Сондықтан ол АВ қабырғасына
тұрғызылған орта перпендикулярдың бойында
жатады, ал ол түзу М нүктесі арқылы өтеді.
Салу: 1) СD гипотенузасы мен (НСD бойынша НСD тікбұрышты үшбұрышы
2) СН катеті мен (НСМ = (МСD + (НСD бойынша НСМ тікбұрышты
үшбұрышы
3) М нүктесі арқылы МК ( НD түзуі
4) МК ( СD = Е нүктесі
5) СЕ кесіндісінің орта перпендикуляры: n
6) n ( МК ( О нүктесі
7) ((О, ОС) шеңбері
8) ( ( НD = А және В нүктелері
АВС – ізделінді үшбұрыш.
Дәлелдеу: Салу бойынша (НСD – биіктік пен биссектрисаның арасындағы бұрыш,
онда
(DCM = (HCM - (HCD = (MCD + (HCD - (HCD = (MCD.
Егер МК ( ( ( Р (Е – ден өзге нүкте) десек, О РЕ (РЕ – диаметр). Салу
бойынша АВ ( РЕ, онда МА = МВ, яғни Е – АВ кесіндісінің орта
перпендикулярында жатыр. Бұдан (АЕ = (ЕВ, яғни (АСЕ ( (ЕСВ ( СD –
биссектриса.
Зерттеу: Егер ( + ( ( 900 болса, есептің шешімі болмайды. Егер ( + ( ( 900
болса, есептің жалғыз шешімі бар.
Есеп 6: АВСD тіктөртбұрышы берілген. Оның СD қабырғасынан АВМ, BCM,
ADM үшбұрыштары ұқсас болатындай етіп, М нүктесін табыңыз.
Шешуі:
Талдау: Есеп шешілді, яғни ізделінді М нүктесі тұрғызылды делік (8-сурет).
Онда АВМ, BCM, ADM үшбұрыштарының ұқсастықтарын және (С=(D=900

екенін ескеріп, (АМВ = 900 теңдігін аламыз. Ал тікбұрышты үшбұрышқа сырттай
сызылған шеңбердің қасиетін пайдалансақ М(, мұндағы (-диаметрі АВ
болатын шеңбер.
Салу: 1) О – АВ кесіндісінің ортасы
2) ( (О, ОВ) шеңбері
3) ( ( DC = М нүктесі
М – ізделінді нүкте.
Дәлелдеу: М ( ( (АМВ ( 900, ал (А ( (В ( 900 екенін
ескерсек, (МАВ ( 900 - (МАD ( (АМD, дәл осылайша (МВА ( (ВМС. Онда

АМВ ( АМD (ВМС.
Зерттеу: Салу жоспарының 3) қадамына байланысты мына жағдайлар болу мүмкін:
1) ВС ( ОВ, онда ( ( DC қимасы М және М( нүктелерінен құралады да,
есептің екі шешімі болады.
2) ВС = ОВ, онда ( ( DC = М – жалғыз нүкте, олай болса, есептің бір ғана
шешімі бар.
3) ВС ( ОВ, онда ( ( DC = (, яғни есептің шешімі жоқ.

Кейбір геометриялық салуларды тек бір құралдың көмегімен де шешуге
болады. Мысалы, тек циркульдың көмегімен шешілетін салу есебін
қарастырайық:
Есеп 7: Тек циркульды пайдаланып, берілген тікбұрышты үшбұрышқа
іштей шеңбер сызыңыз.
Шешуі:
Талдау: Айталық АВС – катеттері а, в, гипотенузасы с болатын берілген
тікбұрышты үшбұрыш, ал ( - оған іштей сызылған ізделінді шеңбер (9-сурет).
Центрі А, радиусы в болатын шеңбер жүргізіп,
Оның гипотенузамен қимасын М деп, ал центрі
В, радиусы а болатын шеңбердің гипотенузамен
қимасын N деп белгілесек, онда МN = BN – BM=
a – (c – в) = a + в – c.
Бұл сан үшбұрышқа іштей сызылған шеңбердің
диаметрі болады (есептен кейінгі ескертуде
дәлелденіп көрсетіледі).Олай болса MN кесіндісін
екіге бөлу арқылы ізделінді шеңбердің радиусын
аламыз. Ал оның центрін табу үшін оның катеттерден қашықтықта
жататынын және (S, SN) шеңберіне тиістілігін ескереміз, мұндағы S – іштей
сызылған шеңбердің гипотенузамен жанасу нүктесі.
Салу: 1) ω1(А, в) шеңбері
2) ω2(В, а) шеңбері
3) ω1∩ АВ = М нүктесі
4) ω2∩ АВ = N нүктесі
5) ω3(N, MN) шеңбері
6) ω4(M, MN) шеңбері
7) ω3 ∩ ω4 = D нүктесі (D – АВС
үшбұрышының сыртындағы нүкте)
8) ω5(D, MN) шеңбері
9) ω5 ∩ ω3 = E нүктесі (М – нан өзге)
10) ω6(Е, MN) шеңбері
11) ω6 ∩ ω3 = F нүктесі (D – дан өзге)
12) ω7(F, MF) шеңбері
13) ω7 ∩ ω4 = L,K нүктелері
14) ω8(K, MN) шеңбері
15) ω9(L, MN) шеңбері
16) ω8 ∩ ω9 = S нүктесі (М – нан өзге)
17) ω10(S, SM) шеңбері
18) ω11(C, SN) шеңбері
19) ω11 ∩ CA = R нүктесі

20) ω12(R, CR) шеңбері
21) ω12 ∩ ω10 = O нүктесі
ω(O, MS) – ізделінді шеңбер
Дәлелдеу: ω10 шеңберінен SM = SO = SN (S - шеңбердің центрі, ал M, O, N
оның бойындағы нүктелер (10-сурет)). Онда SM = SO = SN = = r,
яғни OS = r. Салу бойынша OR = r, онда АС – жанама ( АС ( OR және АС (
ВС ( OR((BC. О нүктесінен ОТ((АС түзуін жүргізсек (Т ( ВС), ТОRС –
тіктөртбұрыш. Ал OR = CR = r болғандықтан, TORC– квадрат, яғни OT=CR=r.
Демек ω(O, MS) немесе ω(O, OR) – ізделінді шеңбер.
Зерттеу: а ( с, в ( с болғандықтан, салу жоспарының 1) – 15)
қадамдары бірмәнді орындалады. К нүктесінен АВ қабырғасына түсірілген
перпен-дикулярдың табанын Р деп белгілесек, 16) салу орындалу үшін МК ( РК
шарты орындалу керек.
MF ( MN ( PK ( DS.
MD = ( 2MD = және MD = MN (
DS = MN немесе DS = MK.
PK ( MK, онда MK ( PK.
( 1, сондықтан МК ( РК. Олай болса, ω8 ∩ ω9 = S нүктесі табылады.
Қалған салу қадамдары да бірмәнді. Сонымен көрсетілген тәсілмен шешілген
есептің жалғыз шешеімі бар және басқа әдіспен шешкенде өзге шешімнің болуы
мүмкін емес, өйткені үшбұрышқа тек бір ғана шеңбер іштей сызылады.
Ескерту: MN = 2r, яғни MN = d екенін дәлелдейік (9-сурет).
Салу бойынша BC = BN болғандықтан, ВТ1 - әрі медиана, әрі биссектриса, әрі
биіктік, онда ВТ1 – CN кесіндісінің орта перпендикуляры, яғни СТ1 = T1N.
Онда СВNT1 төртбұрышында BN + CT1 = BC + T1N, яғни ω - СВNT1 төртбұрышына
іштей сызылған, онда Т1N – жанама. Дәл осылайша Т2М түзуі де ω шеңберіне
жанама болады. Енді Т1N (( Т2М екенін дәлелдейік. Т1 ( в және СТ1 (
ВС болғандықтан, Т1 нүктесінен АВ–ға дейінгі қашықтық СТ1 болады. Ал
дәлелдеу бойынша СТ1 = T1N, онда T1N ( MN. Дәл осылайша Т2М ( MN.
Сонда соңғы екі қатынастан Т1N (( Т2М, онда MN = d.

ІІ тарау. Салу есептерін шешу әдістері
Салу есептерін шешудің бірнеше әдістері бар. Оларға НГО (нүктелердің
геометриялық орны) әдісі, түрлендірулер әдісі (параллель көшіру, осьтік
симметрия, центрлік симметрия, бұру, ұқсас түрлендіру, гомотетия),
алгебралық әдіс және инверсия әдісі жатады.
§1. НГО әдісі
1.1. НГО ұғымы
Геометриялық фигура әр түрлі тәсілмен беріледі: фигуралардың
қиылысуы немесе бірігуі түрінде; фигураны анықтайтын қасиеттердің
көрсетілуі арқылы; т.б.. Мысалы, АВ кесіндісі (11-сурет)
1) АМ, ВN сәулелерінің қиылысуы
2) р түзуіне перпендикуляр болатын (
шеңберінің диаметрі
3) р түзуіне параллель болатын ( шең-
берінің хордаларының орталарының
жиыны түрінде берілуі мүмкін.

Егер фигура әрбір нүктесінің қасиетін көрсету арқылы берілсе, онда
оны көрсетілген қасиетті қанағаттандыратын НГО деп, ал берілген қасиетті
НГО-ң характеристикалық қасиеті деп атайды. Жоғардағы мысалда АВ кесіндісі
р түзуіне параллель ( шеңберінің хордаларының орталарының геометриялық
орны болып табылады.
Салу есептерін шешуде пайдаланылатын геометриялық орындар әдісінің
мәнісі мынада: айталық, салу есебін шешкенде екі шартты бірдей
қанағаттандыратын Х нүктесін табу керек болсын. Бірінші шартты қанағат-
тандыратын нүктелердің геометриялық орны қайсыбір Ғ1 фигурасы болады, ал
екінші шартты қанағаттандыратын нүктелердің геометриялық орны қайсыбір Ғ2
фигурасы болады. Ізделінді Х нүктесі Ғ1 фигурасына да, Ғ2 фигурасына да
тиісті, яғни олардың қиылысу нүктесі болып табылады. Егер бұл гео-метриялық
орындар қарапайым болса (мысалы, түзулер мен шеңберлерден құралса), біз
оларды сала аламыз және қажетті Х нүктесін тауып алуға болады.
НГО сызық немесе бірнеше сызықтардың бірігуі ғана емес, сонымен
қатар нүктелердің жиыны, жазықтықтың бөлігі, т.б. болу мүмкін. Кейде
көрсетілген қасиетті қанағаттандыратын НГО болмайды.
Ф фигурасы көрсетілген қасиетті қанағаттандыратын НГО екенін дәлелдеу
үшін төмендегі өзара қарама - қарсы екі сөйлемді дәлелдеу керек:
1. Ф фигурасының әр нүктесі көрсетілген қасиетке ие болады
2. Көрсетілген қасиетті қанағаттандыратын әрбір нүкте Ф фигурасына
тиісті.
Мысал: Параллель а,в түзулері және оларға перпендикуляр с түзуі берілген.
Осы үш түзуден бірдей қашықтықта жататын жазықтық нүктелерінің гео-
метриялық орнын анықта.
Шешуі: Айталық а ( с ( А, в ( с ( В (12-сурет). АВ кесіндісінің ортасы
арқылы р (( а (р (( в) болатындай р түзуін жүргізіп, осы түзуден с
түзуінің екі жағыннан қашықтықтағы нүктелерді Р1, Р2 деп
белгілейміз.
Сонда Р1, Р2 нүктелерінің әрқайсысы беріл-
ген түзулерден бірдей қашықтықта жатады.
Жазықтықта осы қасиетті қанағаттандыратын
басқа нүктелер жоқ. Шынында да М нүктесі р
түзуінде жатпайды, сондықтан ол а,в түзулері-
нен бірдей қашықтықта болмайды; N нүктесі
р түзуіне тиісті, бірақ Р1, Р2 нүктелерімен беттеспейді, онда ол а, с
түзулерінен бірдей қашықтықта емес. Олай болса, Р1, Р2 нүктелерінің қосы
а, в, с түзулерінен бірдей қашықтықтағы НГО болып табылады.
1.2. Қарапайым НГО
Геометриялық салуларда кездесетін қарапайым НГО-ның мысалдары:
1. Берілген екі нүктеден бірдей қашықтықтағы НГО берілген нүктелерді
қосатын кесіндінің орта перпендикуляры болады. Бұл НГО кейде берілген
нүктелердің симметриясы немесе медиатриссасы деп аталады.
2. Берілген түзуден берілген қашықтықтағы НГО берілген түзуге параллель
және әрқайсысы одан берілген қашықтықта жататын түзулердің қосы болады. Оны
салу үшін берілген түзуге кез-келген перпендикуляр тұрғызып, оның бойынан
берілген түзуден берілген қашықтықта екі нүкте белгілейміз.Сол нүктелер
арқылы өтіп берілген түзулерге параллель болатын түзулер ізделінді НГО
болады.
3. Берілген екі параллель түзуден бірдей қашықтықтағы НГО берілген
түзулердің симметрия осі болады, оны орта сызық, деп те атайды. Бұл НГО-ны
салу үшін берілген а, в түзулерін қиятын кез-келген с түзуін жүргізіп,
оның берілген түзулер арасындағы кесіндісінің ортасы арқылы а-ға (немесе
в-ға) параллель түзу жүргіземіз.
4. Жазықтықтың қиылысушы екі түзуінен бірдей қашықтықтағы НГО берілген
түзулер құрайтын бұрыштардың өзара перпендикуляр екі биссектрисасы болады.
Оны салу қарапайым бұрышты тең екіге бөлу есебіне келеді.
5. АВ кесіндісінен тік бұрыш арқылы көрінетін НГО АВ диаметрі болатын
шеңберді құрайды. Оны салу үшін АВ кесіндісінің ортасы центрі, АВ2
радиусы болатын шеңбер жүргіземіз.
6. АВ кесіндісі берілген φ бұрышымен (φ ≠ 900 және φ ≠ 1800) көрінетіндей
НГО ұштары А, В нүктелері (А, В нүктелерінсіз) болатын, АВ түзуіне
қарағанда симметриялы екі доға болады.
7. Берілген шеңбер φ бұрышымен (φ ≠ 1800) көрінетін НГО радиусы берілген
шеңбер радиусынан үлкен және берілген шеңберге концентрлі шеңберлер
болады.
8. Берілген нүктеден берілген қашықтықтағы НГО - берілген нүкте центрі,
берілген қашықтық радиусы болатын шеңбер.
9. Берілген А, В нүктелерінің әрқайсысына дейінгі қашықтықтарының қатынасы
тұрақты және 1-ден өзге болатын НГО центрлері АВ түзуінің бойында жататын
шеңберлер болады.
10. Берілген А, В нүктелеріне дейінгі қашықтықтарының қосындысы а2 болатын
НГО
- егер 2а2 АВ2 болса, шеңбер болады және оның центрі АВ кесіндісінің
бойында жатады;
- егер 2а2 = АВ2 болса, центрі АВ кесіндісінің ортасында жататын
шеңбер болады;
- егер 2а2 АВ2 болса, құр жиын болады.
11. (О, ОА) шеңберінің А нүктесі арқылы жүргізілген барлық хордаларды
берілген λ (λ 0) қатынасында бөлетін нүктелердің жиыны центрі ОА тү-
зуінде жататын және А нүктесі арқылы өтетін (А нүктесінің өзі алынбайды)
шеңбер болады.
1.3. НГО іздеу
Геометриялық салулардың ішінде НГО–нын табу есептері жиі кездеседі.
Мұндай есептерде кейбір қарапайым немесе элементар фигуралардың бірігуі
белгілі деп алынып, осы бірігудің қай элементі ізделінді ГО–ды
қанағаттандыратанын тауып, көрсету керек. НГО табу есептерін шешу
методикасы талдау, салу, дәлелдеу және зерттеуден тұрады.
Талдаудың мақсаты – ізделінді НГО–ның қандай болатыны жөнінде болжам
жасау. Әдетте, талдауды берілген фигуралардың сызбасын салып, сол сызбадан
ізделінді НГО-а тиісті бір нүктені қарастырудан бастайды. Сонан соң осы
нүкте мен берілген элементтер арасында ГО–ның формасы мен орналасуын
анықтауға мүмкіндік ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.