Скалярлық және векторлық өлшемдері бар көпөлшемді сызықтық бағдарламалау: симплекс әдісі, Парето талдауы және LVO бағдарламалық кешенін әзірлеу


Мазмұны
Кіріспе
. Скаляр және векторлық өлшемдері бар сызықтық бағдарламалау есептерін шешу
. 1 сызықтық бағдарламалауды оңтайландыру мәселесі. Сызықтық бағдарламалау есептерінің түрлері
. 2 негізгі ZLP шешімінің болуы және оны табу жолдары
. 3 симплекс әдісімен сызықтық бағдарламалау есептерін шешу
. 4 өлшемдердің салыстырмалы маңыздылығы туралы сандық ақпарат негізінде шешім қабылдау
. 4. 1 шешімдерді таңдау
. 4. 2 векторлық өлшем және артықшылық қатынасы
. 4. 3 Көп Парето
. 5 Көп өлшемді симплекс әдісі
. 6 міндет қою
. Сызықтық векторлық оңтайландырудың бағдарламалық кешені (LVO)
. 1 LVO PC архитектурасын жобалау
. 2 LVO ДК интерфейсін жобалау
. 3 LVO компьютерінің жұмысын жобалау
. 4 әзірлеу құралдарын таңдау
. 5 LVO ДК бағдарламалық жасақтамасын іске асыру
. 5. 1 бастапқы деректер
. 5. 2 MLP шешу кезеңдері
. 5. 3 Жүйелік талаптар
. 5. 4 ОЖ орнатуға қойылатын талаптар
. Сандық мысал шешімі
. Экономикалық бөлім
. 1 Экономикалық бөлімге кіріспе
. 2 жобаның еңбек сыйымдылығын есептеу
. 3 жалақы шығындарын анықтау
. 4 материалдық шығындарды анықтау.
. 5 үстеме шығыстарды анықтау
. 6 Жобаның өзіндік құнын анықтау
. Жобаның қауіпсіздігі мен экологиялылығы
. 1 ДК-мен жұмыс істеуге арналған үй-жайларға қойылатын талаптар
. 2 компьютер пайдаланушыларының жұмыс орындарын ұйымдастыруға қойылатын талаптар
. 3 жұмыс орындарындағы микроклиматқа қойылатын талаптар
. 4 жұмыс орындарындағы шу мен діріл деңгейіне қойылатын талаптар
. 5 жұмыс орындарында жарықтандыруға қойылатын талаптар
. 6 зиянды әсерлерден қорғаудың негізгі әдістері
. 7 Қорғаныс сүзгілері
. 8 өрт қауіпсіздігі
. 9 электр қауіпсіздігін қамтамасыз ету
Қорытынды
Әдебиеттер тізімі
А Қосымшасы
Б Қосымшасы
В Қосымшасы
Кіріспе
Көптеген әлеуметтік-экономикалық және техникалық нысандар, олардың жұмыс істеуін модельдеу үшін оларды ресімдеу кезінде оңтайландыру әдістерін қолдануға мүмкіндік беретіні белгілі. Сонымен қатар, мұндай әдістердің кең класы сызықтық бағдарламалық міндеттер шеңберіне сәйкес келеді. Ресми деңгейдегі мұндай тапсырмалар сызықтық шектеулермен берілген олардың рұқсат етілген мәндерінің жиынындағы дәлелдер жиынтығынан сызықтық мақсатты функцияны азайту болып табылады. Көбінесе объектінің жұмыс істеу мақсаты бір критерий бойынша таусылмайды, бірақ мұндай критерийлер жиынтығы немесе қатаң түрде көрсетілген, мақсатты функция енді скаляр шама емес, вектор болып табылады. Басқаша айтқанда, сызықтық бағдарламалаудың классикалық есебі (LP) көп өлшемді сызықтық бағдарламалау (MLP) міндетіне айналады.
Шешім қабылдау теориясы аясында осындай мәселелерді шешудің конструктивті аппараты жасалды. Бұл тезис белгілі белгілі әдістерге негізделген MLP мәселелерін шешу процесінің бағдарламалық жасақтамасын жасауға арналған.
1. СКАЛЯР ЖӘНЕ ВЕКТОРЛЫҚ ӨЛШЕМДЕРІ БАР СЫЗЫҚТЫҚ БАҒДАРЛАМАЛАУ ЕСЕПТЕРІН ШЕШУ
. 1 СЫЗЫҚТЫҚ БАҒДАРЛАМАЛАУДЫ ОҢТАЙЛАНДЫРУ МӘСЕЛЕСІ. СЫЗЫҚТЫҚ БАҒДАРЛАМАЛАУ ЕСЕПТЕРІНІҢ ТҮРЛЕРІ
Қазіргі уақытта оңтайландыру ғылымда, техникада және адам қызметінің кез-келген саласында қолданылады.
Оңтайландыру-тиісті жағдайларда жақсы нәтиже алудан тұратын мақсатты қызмет.
Оңтайлы шешімдерді іздеу арнайы математикалық әдістердің құрылуына алып келді және 18 ғасырда оңтайландырудың математикалық негіздері қаланды (вариациялық есептеу, сандық әдістер және т. б. ) . Алайда, 20 ғасырдың екінші жартысына дейін ғылым мен техниканың көптеген салаларында оңтайландыру әдістері өте сирек қолданылды, өйткені математикалық оңтайландыру әдістерін іс жүзінде қолдану КОМПЬЮТЕРЛЕРСІЗ жүзеге асыру өте қиын және кейбір жағдайларда мүмкін емес үлкен есептеу жұмыстарын қажет етті.
Оның тұжырымына байланысты кез - келген оңтайландыру мәселелерін әртүрлі әдістермен шешуге болады, және керісінше-кез-келген әдісті көптеген мәселелерді шешу үшін қолдануға болады. Оңтайландыру әдістері скаляр (оңтайландыру бір критерий бойынша жүзеге асырылады), векторлық (оңтайландыру көптеген критерийлер бойынша жүзеге асырылады), іздеу (тұрақты әдістер мен кездейсоқ іздеу әдістерін қамтиды), аналитикалық (дифференциалды есептеу әдістері, вариациялық есептеу әдістері және т. б. ), есептеу (сызықтық, сызықты емес, дискретті, динамикалық, стохастикалық, эвристикалық және т. б. болуы мүмкін математикалық бағдарламалауға негізделген), теориялық-ықтималдық, теориялық-ойын және т. б. оңтайландыруға шектеулер сияқты мәселелер, және оларсыз.
Оңтайландырудың ең көп қолданылатын әдісі-сызықтық бағдарламалау. Сызықтық бағдарламалау-математикалық бағдарламалаудың алғашқы және егжей-тегжейлі зерттелген бөлімдерінің бірі. Сызықтық бағдарламалау есептерінің қатарына есептерді жатқызуға болады:
шикізат пен материалдарды ұтымды пайдалану негіздері;
пішуді оңтайландыру міндеттері;
кәсіпорындардың өндірістік бағдарламасын оңтайландыру;
оңтайлы орналастыру және өндірісті шоғырландыру;
тасымалдаудың, көлік жұмысының оңтайлы жоспарын жасау негіздері;
өндірістік қорларды басқару;
. және оңтайлы жоспарлау саласына жататын көптеген басқалар.
LP міндеттері-бұл объективті функция да, теңдік пен теңсіздік түріндегі шектеулер де сызықты болатын міндеттер. Қысқаша айтқанда, сызықтық бағдарламалау мәселесін келесідей тұжырымдауға болады: сызықтық теңдіктер немесе теңсіздіктер түрінде m шектеулері бар сызықтық объективті функцияның экстремумын жеткізетін айнымалылар мәндерінің векторын табыңыз[2] .
Сәйкес анықтау, міндет ЛП жазылуы мүмкін түрінде
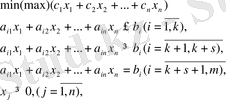
шамалары қайда
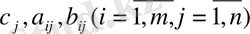 олар R нақты сандар өрісінің F кіші аймағының элементтері болып табылады, LP есебінің бұл формасы жалпы деп аталады.
олар R нақты сандар өрісінің F кіші аймағының элементтері болып табылады, LP есебінің бұл формасы жалпы деп аталады.
LP түрінің міндеті
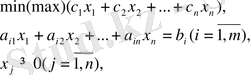
канондық деп аталады, ал LP түрінің міндеті
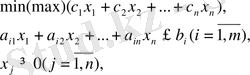
стандартты (қалыпты) деп аталады.
Сонымен қатар, теңдіктің оң жақтары теріс емес болуы үшін (бұл сыни емес болса да) талап етіледі, яғни. шарттар сақталуы керек
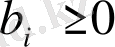 (
(
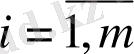 ) .
) .
Болсын
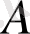 - матрица с
- матрица с
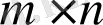 элементтері
элементтері
 ,
,
 - вектор-баған
- вектор-баған
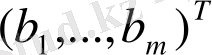 а
а
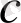 - вектор-жол
- вектор-жол
 LP есебінің канондық және стандартты формаларын сәйкесінше матрицалық түрде жазуға болады
LP есебінің канондық және стандартты формаларын сәйкесінше матрицалық түрде жазуға болады
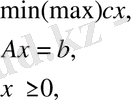 және
және
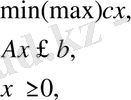
Мәселені шешудің кез-келген әдісін жүзеге асыру үшін әдетте стандартты формадан канондық формаға өту керек [2] . Бұған әр теңсіздікке түр қосу арқылы қол жеткізіледі
 айнымалы
айнымалы
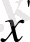 . Осылайша,
. Осылайша,
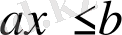
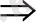
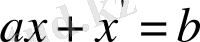 .
.
Мақсатты функцияның максимумынан минимумға ауысу үшін

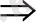
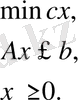
1. 2 НЕГІЗГІ ЗЛП ШЕШІМІНІҢ БОЛУЫ ЖӘНЕ ОНЫ ТАБУ ТӘСІЛДЕРІ
Сызықтық бағдарламалаудың негізгі міндетін қарастырыңыз: x1, x2, . . . , xn айнымалыларының теріс емес мәндерін табыңыз, олар m шарттарына - теңдіктерге сәйкес келеді
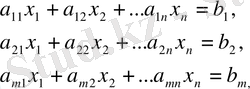 (1)
(1)
және осы айнымалылардың сызықтық функциясын максимумға айналдыру
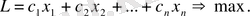 (2)
(2)
Қарапайым болу үшін, барлық шарттар (1) сызықты тәуелсіз (r=m) деп есептейік және біз осы болжамда пайымдау жүргіземіз.
(1) шарттарды қанағаттандыратын x1, x2, . . . , xn теріс емес мәндерінің кез-келген жиынтығын OZLP рұқсат етілген шешім деп атаймыз. Оңтайлы деп атайық онда рұқсат етілген шешімдер, ол аударады, бұл максимум функциясын (2) . Оңтайлы шешім табу қажет.
Бұл тапсырманың әрқашан шешімі бар ма? Жоқ, әрқашан емес.
ZLP шешілмейді (оңтайлы шешімі жоқ) :
Шектеу жүйесінің сәйкес келмеуіне байланысты. Яғни, жүйеде 1-суретте көрсетілгендей бірде-бір шешім жоқ.

1-сурет-шектеулер жүйесінің сәйкессіздігі
Үшін неограниченности мақсатты функциясы көптеген шешімдер. Басқаша айтқанда, Max - та ZLP-ны шешкен кезде, мақсатты функцияның мәні шексіздікке, ал min-де ZLP жағдайында-2-суретте көрсетілгендей шексіздікке жетеді.
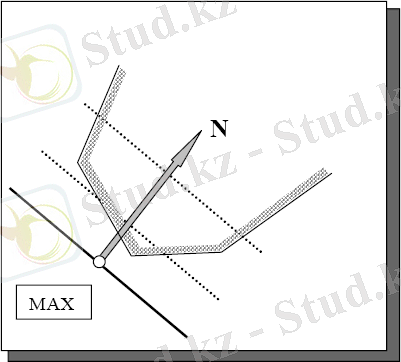
2-сурет-көптеген шешімдердегі объективті функцияның шексіздігі
ЗЛП рұқсат етілсін:
Шешімдер жиынтығы бір нүктеден тұрады. Бұл 3-суретте көрсетілгендей оңтайлы.
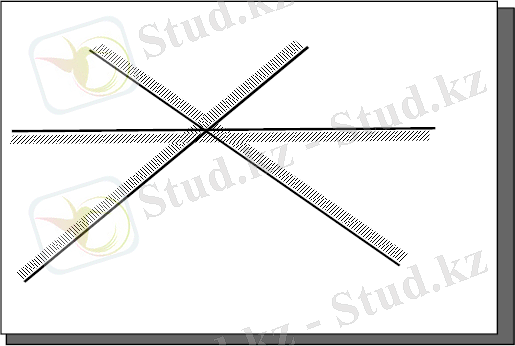
3-сурет-шешімдер жиынтығы бір нүктеден тұрады
Жалғыз оңтайлы шешім ZLP. Шекті позициядағы мақсатты функцияға сәйкес келетін түзу 4-суретте көрсетілгендей бір нүктеде көптеген шешімдермен қиылысады.

4-сурет-жалғыз оңтайлы шешім
ZLP оңтайлы шешімі жалғыз емес. N векторы көптеген шешімдердің бір жағына перпендикуляр. Бұл жағдайда 5-суретте көрсетілгендей АВ кесіндісіндегі кез келген нүкте оңтайлы болып табылады[2] .
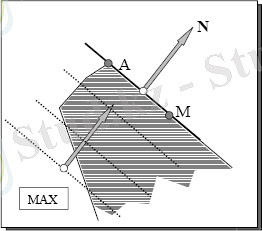
5-сурет-оңтайлы шешім жалғыз емес
. 3 СИМПЛЕКС ӘДІСІМЕН СЫЗЫҚТЫҚ БАҒДАРЛАМАЛАУ ЕСЕПТЕРІН ШЕШУ
Симплекс әдісі-мақсатты функцияның мәнін жақсарту бағытында рұқсат етілген шешімдер аймағының бұрыштық нүктелерін санауды жүзеге асыратын LP мәселесін шешу алгоритмі.
Бұл әдісті дипломдық жобада қолдану LP мәселесін шешу үшін келесі факторларға байланысты:
- әдіс әмбебап, кез-келген сызықтық бағдарламалау проблемасына канондық түрде қолданылады;
- әдістің алгоритмдік сипаты оны техникалық құралдардың көмегімен сәтті бағдарламалауға және жүзеге асыруға мүмкіндік береді.
Мақсатты функцияның экстремумына әрқашан рұқсат етілген шешімдер аймағының бұрыштық нүктелерінде қол жеткізіледі. Ең алдымен, рұқсат етілген бастапқы (анықтамалық) шешім, яғни. рұқсат етілген шешімдер аймағының кез-келген бұрыштық нүктесі. Әдіс процедурасы бұл шешім оңтайлы ма деген сұраққа жауап беруге мүмкіндік береді. Егер " иә " болса, онда мәселе шешіледі. Егер" жоқ " болса, онда мақсатты функцияның мәні жақсаратын рұқсат етілген шешімдер аймағының іргелес бұрыштық нүктесіне өту жүзеге асырылады. Рұқсат етілген шешімдер аймағының бұрыштық нүктелерін санау процесі мақсатты функцияның экстремумына сәйкес келетін нүкте табылғанша қайталанады [3] .
Көпбұрыштың шыңдарының саны шектеулі болғандықтан, қадамдардың соңғы саны үшін оңтайлы мәнді табуға немесе мәселенің шешілмейтіндігін анықтауға кепілдік беріледі.
Мұндағы шектеулер жүйесі-сызықтық теңдеулер жүйесі, онда белгісіздер саны теңдеулер санынан көп болады. Егер жүйенің дәрежесі тең болса, онда қалған белгісіздерді білдіретін белгісіздерді таңдауға болады. Сенімділік үшін, әдетте, бірінші, қатарынан белгісіз таңдалған деп саналады . Бұл белгісіз (айнымалылар) негізгі деп аталады, қалғандары бос. Негізгі айнымалылардың саны әрқашан шектеулер санына тең.
Белгілі бір мәндерді еркін айнымалыларға тағайындау және негізгі мәндерді есептеу (бос мәндер арқылы көрсетілген) шектеулер жүйесінің әртүрлі шешімдерін алады. Еркін айнымалылар нөлге тең болған жағдайда алынған шешімдер ерекше қызығушылық тудырады. Мұндай шешімдер негізгі деп аталады. Негізгі шешім, егер онда айнымалы мәндер болса, рұқсат етілген негізгі шешім немесе тірек шешім деп аталады. Ол барлық шектеулерге сәйкес келеді.
Шектеу жүйесімен олар осы жүйенің кез-келген негізгі шешімін табады. Егер табылған алғашқы негізгі шешім қолайлы болса, онда олар оны оңтайлылыққа тексереді. Егер ол оңтайлы болмаса, онда басқа рұқсат етілген негізгі шешімге көшу жүзеге асырылады.
Симплекс әдісі осы жаңа шешіммен сызықтық форманың оңтайлы деңгейге жетпесе, оған жақындауын қамтамасыз етеді. Жаңа рұқсат етілген негізгі шешіммен олар оңтайлы шешім тапқанша бірдей әрекет етеді.
Егер табылған алғашқы негізгі шешім қолайсыз болып шықса, онда симплекс әдісін қолдана отырып, басқа негізгі шешімдерге көшу шешімнің қандай-да бір қадамында негізгі шешім қабылданғанға дейін жүзеге асырылады немесе шектеулер жүйесінің сәйкессіздігі туралы қорытынды жасауға болады[3] .
Осылайша, симплекс әдісін қолдану екі кезеңге бөлінеді:
шектеу жүйесінің рұқсат етілген негізгі шешімін табу немесе оның сәйкес келмеу фактісін анықтау;
шектеу жүйесінің үйлесімділігі жағдайында оңтайлы шешімді табыңыз.
Келесі рұқсат етілген шешімге өту алгоритмі келесідей:
мақсатты функцияның коэффициенттер жолында максимумды табу кезінде ең аз теріс сан таңдалады. Реттік нөмірі коэффициент -
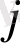 .
.
Егер жоқ болса, онда бастапқы негізгі шешім оңтайлы;
-матрица элементтерінің арасындағы
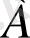 баған нөмірімен
баған нөмірімен
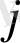 (бұл баған жетекші немесе шешуші деп аталады) оң элементтер таңдалады. Егер жоқ болса, онда мақсатты функция айнымалылардың рұқсат етілген мәндерінің аймағында шектеусіз және шешім тапсырмасында жоқ;
(бұл баған жетекші немесе шешуші деп аталады) оң элементтер таңдалады. Егер жоқ болса, онда мақсатты функция айнымалылардың рұқсат етілген мәндерінің аймағында шектеусіз және шешім тапсырмасында жоқ;
-матрицаның жетекші бағанының таңдалған элементтерінің арасында
 тиісті бос мүшенің осы элементке қатынасының мәні минималды болатын біреуін таңдаңыз. Бұл элемент жетекші деп аталады, ал ол орналасқан жол жетекші деп аталады;
тиісті бос мүшенің осы элементке қатынасының мәні минималды болатын біреуін таңдаңыз. Бұл элемент жетекші деп аталады, ал ол орналасқан жол жетекші деп аталады;
осылайша, жетекші элементтің жолына сәйкес келетін негізгі айнымалы бос санға ауыстырылуы керек, ал жетекші элементтің бағанына сәйкес келетін бос айнымалы негізгі санға енгізілуі керек. Негізгі айнымалылардың жаңа нөмірлері бар жаңа шешім жасалады.
Есепті максимумға шешкен кезде жоспардың оңтайлылығының шарты: мақсатты функцияның коэффициенттерінің арасында теріс элементтер жоқ [4] .
1. 4 ӨЛШЕМДЕРДІҢ САЛЫСТЫРМАЛЫ МАҢЫЗДЫЛЫҒЫ ТУРАЛЫ САНДЫҚ АҚПАРАТ НЕГІЗІНДЕ ШЕШІМДЕР ҚАБЫЛДАУ
. 4. 1 ШЕШІМДЕРДІ ТАҢДАУ
Адам өз қызметінде үнемі таңдау жасау керек жағдайларға тап болады. Әр түрлі деңгейлер мен деңгейлердің басшылары үнемі өздері басқаратын бөлімшелерді құруға, белгілі бір стратегиялық мінез-құлық жолын таңдауға, нақты экономикалық және экономикалық шешімдер қабылдауға мәжбүр. Банк қызметкерлері инвестициялау үшін объектілерді таңдайды, кәсіпорындар мен фирмалардың экономистері оңтайлы экономикалық бағдарламаны жоспарлайды және т. б. және т. б.
Таңдаудың практикалық тапсырмаларының тізімін әрі қарай жалғастыруға болады. Біз айтылғанмен шектеліп, кез-келген таңдау міндетіне тән жалпы элементтерді анықтаймыз.
Ең алдымен, таңдау жасалуы керек шешімдер жиынтығы берілуі керек. Біз оны белгілейміз
 біз көптеген мүмкін шешімдерді атаймыз. Шешімдердің табиғаты ешқандай рөл атқармайды. Бұл жобалық шешімдер, мінез-құлық нұсқалары, саяси немесе экономикалық стратегиялар және т. б. болуы мүмкін.
біз көптеген мүмкін шешімдерді атаймыз. Шешімдердің табиғаты ешқандай рөл атқармайды. Бұл жобалық шешімдер, мінез-құлық нұсқалары, саяси немесе экономикалық стратегиялар және т. б. болуы мүмкін.
Шын мәнінде, шешімдерді таңдау (немесе қабылдау) таңдалған (ең жақсы немесе оңтайлы) деп жарияланған барлық мүмкін шешімдердің ішінен нұсқау болып табылады, дегенмен кейбір жағдайларда мүмкін болатын көптеген шешімдердің белгілі бір жиынтығы болып табылатын шешімдердің біреуін емес, тұтас жиынтығын таңдау керек
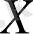 .
.
Біз көптеген оңтайлы (таңдалған) шешімдерді белгілейміз
 . Бұл таңдау мәселесін шешуді білдіреді. Таңдау мәселесін шешу-көпті табуды білдіреді
. Бұл таңдау мәселесін шешуді білдіреді. Таңдау мәселесін шешу-көпті табуды білдіреді
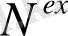 , мүмкін болатын көптеген шешімдердің белгілі бір жиынтығы. Атап айтқанда
, мүмкін болатын көптеген шешімдердің белгілі бір жиынтығы. Атап айтқанда
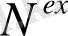 , бір элементті жиын болуы мүмкін.
, бір элементті жиын болуы мүмкін.
Таңдау процесі өз мақсаттарына жету үшін осы таңдауды жүзеге асыратын адамсыз мүмкін емес. Адам (немесе белгілі бір мақсатқа жетуге бағынатын бүкіл ұжым), таңдау жасайды және оның салдары үшін толық жауап береді, шешім қабылдаушы (шешім қабылдаушы) деп аталады[5] .
1. 4. 2 ВЕКТОРЛЫҚ ӨЛШЕМ ЖӘНЕ АРТЫҚШЫЛЫҚ ҚАТЫНАСЫ
Төменде бірнеше сандық функциялар болған жағдайға арналған
 ,
,
 ≥
≥
 , жиынында анықталған
, жиынында анықталған
 .
.
Таңдау мәселесінің мазмұнына байланысты бұл функциялар оптималдылық критерийлері, тиімділік критерийлері, мақсатты функциялар, индикаторлар немесе сапа критерийлері деп аталады.
Біз ең жақсы жобалық шешімді таңдау мәселесін қарастыра отырып, енгізілген терминдерді суреттейміз. Бұл тапсырмада көп нәрсе бар
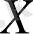 бірнеше конкурстық жобалардан тұрады (мысалы, жаңа кәсіпорын салу), ал оңтайлылық өлшемдері жобаны іске асыру құны болуы мүмкін
бірнеше конкурстық жобалардан тұрады (мысалы, жаңа кәсіпорын салу), ал оңтайлылық өлшемдері жобаны іске асыру құны болуы мүмкін
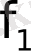
және пайда мөлшері
 , бұл жобалық шешімді (яғни салынған кәсіпорын) қамтамасыз етеді. Егер сіз осы мәселені қарастыруды оңтайлылықтың бір ғана критерийімен шектесеңіз, онда мұндай мәселені шешудің практикалық маңыздылығы шамалы болады. Шын мәнінде, тек бірінші критерийді қолданған кезде ең арзан жоба таңдалады, бірақ оны жүзеге асыру қолайсыз аз пайдаға әкелуі мүмкін. Екінші жағынан, оңтайлылықтың екінші критерийі негізінде таңдалған ең тиімді жобаны салу үшін қолда бар қаражат жеткіліксіз болуы мүмкін. Сондықтан, осы тапсырмада осы екі критерийді бір уақытта ескеру қажет. Егер сіз кәсіпорынның құрылысы мен жұмыс істеуінің жағымсыз экологиялық салдарын азайтуға қосымша тырыссаңыз, онда көрсетілген екеуіне тағы бір - үшінші критерийді қосу керек және т. б. жобаны таңдауды жүзеге асыратын ЛПР-ға келетін болсақ, онда бұл міндет аумағында кәсіпорын салынатын аудан әкімшілігінің басшысы болып табылады, егер бұл кәсіпорын мемлекеттік болып табылса. Егер компания жеке болса, онда тиісті компанияның басшысы LPR ретінде әрекет етеді.
, бұл жобалық шешімді (яғни салынған кәсіпорын) қамтамасыз етеді. Егер сіз осы мәселені қарастыруды оңтайлылықтың бір ғана критерийімен шектесеңіз, онда мұндай мәселені шешудің практикалық маңыздылығы шамалы болады. Шын мәнінде, тек бірінші критерийді қолданған кезде ең арзан жоба таңдалады, бірақ оны жүзеге асыру қолайсыз аз пайдаға әкелуі мүмкін. Екінші жағынан, оңтайлылықтың екінші критерийі негізінде таңдалған ең тиімді жобаны салу үшін қолда бар қаражат жеткіліксіз болуы мүмкін. Сондықтан, осы тапсырмада осы екі критерийді бір уақытта ескеру қажет. Егер сіз кәсіпорынның құрылысы мен жұмыс істеуінің жағымсыз экологиялық салдарын азайтуға қосымша тырыссаңыз, онда көрсетілген екеуіне тағы бір - үшінші критерийді қосу керек және т. б. жобаны таңдауды жүзеге асыратын ЛПР-ға келетін болсақ, онда бұл міндет аумағында кәсіпорын салынатын аудан әкімшілігінің басшысы болып табылады, егер бұл кәсіпорын мемлекеттік болып табылса. Егер компания жеке болса, онда тиісті компанияның басшысы LPR ретінде әрекет етеді.
Жоғарыда көрсетілген сандық функциялар
 векторлық өлшемді құрайды
векторлық өлшемді құрайды
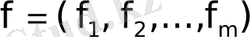 , (3)
, (3)
ол l-өлшемді арифметикалық кеңістіктегі мәндерді қабылдайды ол l-өлшемді арифметикалық кеңістіктегі мәндерді қабылдайды
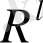 . Бұл кеңістік критериалды кеңістік немесе бағалау кеңістігі деп аталады, және кез-келген мән
. Бұл кеңістік критериалды кеңістік немесе бағалау кеңістігі деп аталады, және кез-келген мән
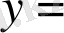
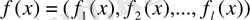
 векторлық өлшем
векторлық өлшем
 белгілі бір жағдайда
белгілі бір жағдайда
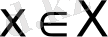 мүмкін шешімді векторлық бағалау деп атайды
мүмкін шешімді векторлық бағалау деп атайды
 [5] .
[5] .
Мүмкін болатын көптеген шешімдерді қамтитын таңдау тапсырмасы
 және векторлық өлшем
және векторлық өлшем
 , әдетте көп өлшемді тапсырма деп аталады.
, әдетте көп өлшемді тапсырма деп аталады.
Формальды міндеттер қою МЛП түрі бар
 (4)
(4)
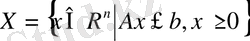 (5)
(5)
Мұнда, әдеттегі LP тапсырмасынан айырмашылығы, c-өлшем матрицасы
 , вектор емес. А-өлшемі шектеулерінің матрицасы
, вектор емес. А-өлшемі шектеулерінің матрицасы
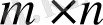 . Осылайша, көп өлшемді (4), (5) тапсырма көпбұрыштағы максимизацияны болжайды
. Осылайша, көп өлшемді (4), (5) тапсырма көпбұрыштағы максимизацияны болжайды
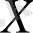 қарапайым тапсырмадағыдай бір сызықтық критерий емес (LP), ао өлшемдері бір уақытта.
қарапайым тапсырмадағыдай бір сызықтық критерий емес (LP), ао өлшемдері бір уақытта.
1. 4. 3 ПАРЕТО ЖИЫНТЫҒЫ
Көп өлшемді таңдау міндетіне оралайық. Онда көптеген мүмкін шешімдерден басқа
 қатынастар мен қалаулар
қатынастар мен қалаулар
 векторлық өлшем де бар
векторлық өлшем де бар
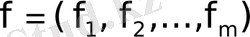 . Құрамдас
. Құрамдас
 векторлық критерий LPR-нің Белгілі бір мақсатын сипаттайды және математикалық тұрғыдан осы мақсатқа жетуге деген ұмтылыс жиынтықта осы компонентті барынша көбейту немесе азайту арқылы көрінеді
векторлық критерий LPR-нің Белгілі бір мақсатын сипаттайды және математикалық тұрғыдан осы мақсатқа жетуге деген ұмтылыс жиынтықта осы компонентті барынша көбейту немесе азайту арқылы көрінеді
 . Сенімділік үшін, барлық жерде біз ЛПР мүмкіндігінше әр компоненттің үлкен мәндерін алуға мүдделі деп санаймыз
. Сенімділік үшін, барлық жерде біз ЛПР мүмкіндігінше әр компоненттің үлкен мәндерін алуға мүдделі деп санаймыз
 векторлық критерий.
векторлық критерий.
Мүмкін болатын шешімді таңдау
 және векторлық өлшемнің мәнін есептеу
және векторлық өлшемнің мәнін есептеу
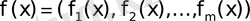 бұл шешімде біз жиынтық аламыз
бұл шешімде біз жиынтық аламыз
 векторлық бағалауды құрайтын сандар
векторлық бағалауды құрайтын сандар
 осы шешімнің
осы шешімнің
 . Осылайша, мүмкін болатын әрбір шешімнің өзіндік векторлық бағасы бар.
. Осылайша, мүмкін болатын әрбір шешімнің өзіндік векторлық бағасы бар.
Енді екі мүмкін шешімді қарастырыңыз
 және
және
 тиісті бағалармен бірге
тиісті бағалармен бірге
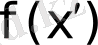 және
және
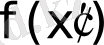 . Бұл бағалар арақатынаспен байланысты делік
. Бұл бағалар арақатынаспен байланысты делік
 , (6)
, (6)
бұл компоненттік теңсіздіктердің әділдігін білдіреді
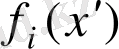 ≥
≥
 барлық нөмірлер үшін
барлық нөмірлер үшін
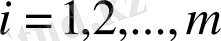 , әрі
, әрі
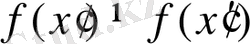 , яғни, кем дегенде бір нөмір үшін
, яғни, кем дегенде бір нөмір үшін
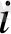
дұрыс қатаң теңсіздік
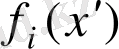 >
>
 .
.
Теңсіздікті орындау (6) барлық компоненттер бойынша бірінші векторлық бағалау екінші векторлық бағалаудың "нашар емес" (дәлірек айтқанда, кем емес) және бірінші бағалаудың кем дегенде бір компоненті екінші бағалаудың сәйкес компонентінен "жақсы" (қатаң үлкенірек) екенін білдіреді. Жоғарыда айтылғандай, ЛПР әр критерий бойынша мүмкін болатын максималды мәнге қол жеткізуге мүдделі болғандықтан, қазіргі жағдайда оған ұсынылған екі шешімнің ішінен ЛПР
 және
және
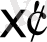 біріншісін анық таңдайды.
біріншісін анық таңдайды.
Басқаша айтқанда, ЛПР-дің векторлық критерийдің әр компонентін барынша арттыруға деген ұмтылысын келесі талап тұрғысынан білдіруге болады: артықшылық қатынасы
 және векторлық өлшем
және векторлық өлшем
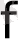 Парето аксиомасына бағынады, яғни теңсіздік орындалған сайын (6) арақатынастың әділдігі жүреді
Парето аксиомасына бағынады, яғни теңсіздік орындалған сайын (6) арақатынастың әділдігі жүреді
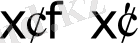 :
:
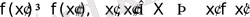 . (7)
. (7)
Егер мүмкін болатын бірнеше шешім үшін теңсіздік (6) орындалса, онда Парето аксиомасының арқасында бірінші шешім екіншіден артық болады. Сонымен, екінші шешім ешқандай жағдайда оңтайлы болмайды және оны келесі таңдау процесінен алып тастауға болады. Осындай шешімдердің барлығын алып тастау көптеген Паретоға әкеледі.
Көптеген парето-оңтайлы шешімдер
 .
.
Шешім
 парет (доминацияланбайтын, жетілдірілмейтін) деп аталады, егер оны кез-келген критерий бойынша жақсарту мүмкін болмаса, кем дегенде біреуінің мәнін нашарлатпайды.
парет (доминацияланбайтын, жетілдірілмейтін) деп аталады, егер оны кез-келген критерий бойынша жақсарту мүмкін болмаса, кем дегенде біреуінің мәнін нашарлатпайды.
Немесе ресми түрде,
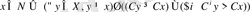
Онда
 -матрицаның i-ші жолы (I-ші критерий)
-матрицаның i-ші жолы (I-ші критерий)
 . Енді біз доминацияланбайтын және парето-оңтайлы шешімдер арасындағы қатынасты орнатамыз. Егер шешім
. Енді біз доминацияланбайтын және парето-оңтайлы шешімдер арасындағы қатынасты орнатамыз. Егер шешім
 парето оңтайлы емес, содан кейін мүмкін болатын шешім үшін
парето оңтайлы емес, содан кейін мүмкін болатын шешім үшін
 теңсіздік орындалды (6) . Парето аксиомасына сәйкес, бұл
теңсіздік орындалды (6) . Парето аксиомасына сәйкес, бұл


 , ал,
, ал,
 - басым шешім. Осылайша, парето оңтайлы емес кез-келген шешім басым болады. Бұдан шығатыны, кез-келген негізсіз шешім Парето оңтайлы болуы керек.
- басым шешім. Осылайша, парето оңтайлы емес кез-келген шешім басым болады. Бұдан шығатыны, кез-келген негізсіз шешім Парето оңтайлы болуы керек.
Таңдаудың нақты практикалық міндеттерін рәсімдеу нәтижесінде көптеген мүмкін шешімдер белгілі болады
 және векторлық өлшем
және векторлық өлшем
 . Векторлық өлшемді және көптеген мүмкін шешімдерді білу Парето жиынтығын (шешімдер және/немесе бағалау) табуға мүмкіндік береді. Көптеген Парето салу көбінесе кез-келген көп өлшемді мәселені шешудегі алғашқы қажетті қадам болып саналады.
. Векторлық өлшемді және көптеген мүмкін шешімдерді білу Парето жиынтығын (шешімдер және/немесе бағалау) табуға мүмкіндік береді. Көптеген Парето салу көбінесе кез-келген көп өлшемді мәселені шешудегі алғашқы қажетті қадам болып саналады.
Қарапайым мысалдарды қарастырудан бір төтенше жағдайда парето-оңтайлы шешімдердің жиынтығы бір элементтен тұруы мүмкін, ал екінші жағдайда-әрбір мүмкін шешім парето - оңтайлы болады. Егер парето-оңтайлы шешім жалғыз болса, онда мұндай проблемада тек парето-оңтайлы шешім оңтайлы болуы мүмкін. Алайда, тәжірибе көрсеткендей, нақты мәселелерде көптеген Парето өте кең және оны құру шешім қабылдау мәселесін толығымен шешпейді. Оңтайлы шешімдерді одан әрі іздеу саласын тарылтуға мүмкіндік беретін әдістер қажет. Бұл әдіс критерийлердің салыстырмалы маңыздылығы теориясы аясында жасалған [6] .
1. 5 КӨП ӨЛШЕМДІ СИМПЛЕКС ӘДІСІ
Әдетте, MLP (4), (5) дәстүрлі шешімі жоқ, яғни нүкте жоқ
 осындай, бұл
осындай, бұл
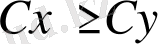 барлық
барлық
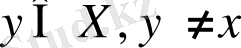 ЛПР-да критерийлердің салыстырмалы маңыздылығына қатысты қандай да бір априорлық ақпарат болмаған жағдайда, (4), (5) мәселені шешу арқылы біз көптеген Паретоны түсінеміз[7] .
ЛПР-да критерийлердің салыстырмалы маңыздылығына қатысты қандай да бір априорлық ақпарат болмаған жағдайда, (4), (5) мәселені шешу арқылы біз көптеген Паретоны түсінеміз[7] .
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz