МАТЕМАТИКАЛЫҚ МАЯТНИК ТЕРБЕЛІСТЕРІН МАТЕМАТИКАЛЫҚ МОДЕЛЬДЕУ

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 43 бет
Таңдаулыға:

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 3-4
І ТАРАУ. МЕХАНИКАЛЫҚ ТЕРБЕЛІСТЕР
§1.1. Гармониялық тербелістер және олардың сипаттамалары ... ... ... ... ... .. ..
§ 1.2. Еркін өшетін механикалық тербелістер ... ... ... ... ... ... ... ... ... ... ... ... ...
§ 1.3. Еріксіз механикалық тербелістер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
§ 1.4. Параметрлік тербелістер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
ІІ ТАРАУ. МАТЕМАТИКАЛЫҚ МАЯТНИК ТЕРБЕЛІСТЕРІН МАТЕМАТИКАЛЫҚ МОДЕЛЬДЕУ
§ 2.1. Математикалық модель туралы ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... .
§ 2.2. Дифференциалдық теңдеуді шешуге арналған сандық әдістер ... ... ... ..
§ 2.3. Жай дифференциалдық теңдеулер туралы жалпы түсінік ... ... ... ... ... ..
§ 2.4. Математикалық маятник тербелістерінің математикалық моделі ... ... .
ІІІ ТАРАУ.
§ 3.1. Физиканы оқытуда компьютерлік технологияны қолданудың негізгі бағыттары ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
§ 3.2. Физикалық құбылыстарды компьютерде модельдеп оқыту әдістері
ҚОРЫТЫНДЫ
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР
ҚОСЫМША
Математикалық маятник тербелістерін математикалық модельдеу қосымшасының

Кіріспе
Ғылым мен техниканың әр түрлі саласындағы физикалық процестер мен
құбылыстарды математикалық модельдеу ғылымның бүгінгі таңдағы
маңызды салаларының бірі. Сандық эксперимент негізінде сандык әдістер
арқылы математикалық модельдеудің есептерін шешу жатыр. Сандық әдістер
күшті, қуатты математикалық құрал. Қазіргі заманғы физика және
техникадағы процестерді сипаттайтын параметрлері әр түрлі болып келетін
математикалық модельдеумен сипатталынады. Бұл теңдеулерді
аналитикалық немесе графикалық әдістер арқылы шығару қиын, мұндай
есептер сандық әдістер арқылы компьютердің көмегімен шығарылады.
Сандық әдістер дамуы, алгоритмдік тілдердің пайда болуы және арнаулы
программалардың жасалуы физика мен техниканын қолданбалы есептерін.
компьютер арқылы шығару аналитикалық әдістерге қарағанда күрделі
есептеулер керек етпейді. Компьютер әр түрлі физикалық жүйелердегі
процестерді зерттеуге мүмкіндік береді.
Сандық теңдеулер жүйесін алгоритм деңгейіне дейін алып келу керек.
Программалау тілдерінің дүниеге келуі есептеу машиналарының дүниеге
келуімен байланысты емес, ол адамзат баласының Жер бетіндегі өмірімен
тығыз байланысты. Біздің ерте заманда өмір сүрген ата-бабаларымыз Жер
бетінде өмір сүрудің тиімді алгоритмдерін ойлап тапқан.
Шындығында, Жер бетінде өмір сүріп жатқан адамдар үлкенді немесе
кішілі программистер. Себебі біз күнделікті өмірімізге жоспар (программа)
жасаймыз және соны шешудің (алгоритм) жолдарын іздейміз.
Компьютерлік программа - машиналық командалардың жиыны, яғни
берілген алгоритмді компьютерде орындататын, яғни программалық форма.
Машиналық кодта компьютерде орындататын, яғни программалық форма.
Машиналық кодта жасалған программалар өте қиын, сондықтан да өткен
ғасырдың 50-жылдарында алгоритмдік программалау тілдері дүниеге келді.
Компьютерлік программа физикалық жүйелердегі процестерді модельдейді
және сандық экспериментін сипаттайды. Сонымен программа
лабораториялық эксперимент пен теориялық есептеуді байланыстыратын
элемент. Алынған нәтижелерді практикалық эксперимент негізінде алынған
нәтижелермен байланыстыра отырып сандық модельдеудің дұрыстылығы
анықталады.
Математикалық модельдеу төменде көрсеткен бөлімдерден тұрады:
Есеп беріледі
Сол есептің Математикалық моделі құрылады;
Математикалық моделдеуге Есептеу математикасының әдістері қолданылады(сандық әдіс);
Алгоритм жазылады
Программа жазылады
Жазылған программа компьютерде теріледі..
Төменде берілген физикалық есептерде Ньютонның екінші заңы - барлық динамиканың негізі іргелі роль атқарады.
Белгілі уақыт моментіндегі дененің алатын үдеуі, осы моменттегі осы денеге әсер ететін күшке тура пропорционал да, дененің массасына кері пропорционал.
Ньютонның екінші заңының өрнегі:
a=Ftmt, үдеуге байланысты берген өрнегі
dυdt=Ftmt, жылдамдыққа байланысты берген өрнегі
d2Sdt2=Ftmt және орын ауыстыруға байланысты алатын болсақ
Физикалық шамалардың ілездік мәндерін байланыстыра отырып, Ньютонның екінші заңы күш пен массаның әртүрлі өзгерістерінде денелердің қозғалысын зерттеуге мүмкіндік береді.

І ТАРАУ. МЕХАНИКАЛЫҚ ТЕРБЕЛІСТЕР
§1.1. Гармониялық тербелістер және олардың сипаттамалары
Гармоникалық тербелмелі қозғалыс деп нүкте қозғалысының тепе-теңдік қалпынан ауытқу шамасының синусоида немесе косинусоида бойымен периодты түрде қайталанып отыруын айтамыз.
Егер тербелістегі нүктенің тепе-теңдік қалпынан ауытқу шамасынын х арқылы белгілесек, онда осы ауытқудың уақытқа байланысты өзгеруі мына формуламен өрнектеледі:
x=Acos(ωt+φ0)
немесе

y=Asin(ωt+φ0) (1.1)
Енді қозғалыстағы нүктенің кинетикасын қарастарайық. А нүктесі радиусы R шеңбер бойымен тұрақты ω бұрыштық жылдамдықпен сағат тіліне қарсы бағытта бірқалыпты қозғалсын.

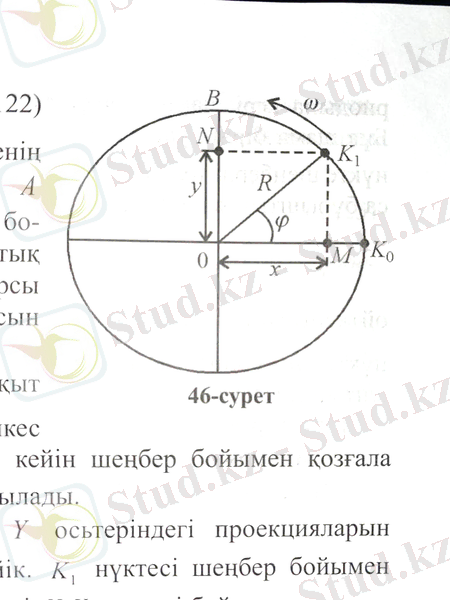
1-сурет
Егер алғашқы t = 0 уақыт мезетіндегі К0-ге сәйкес келсе, онда нүкте t уақыттан кейін шеңбер бойымен қозғала отырып, φ=ωt бұрышына бұрылады.
К1 нүктесінің Х және Ү осьтеріндегі проекцияларын M және N арқылы белгілейік. К1 нүктесі шеңбер бойымен қозғалғандықтан M, N нүктелері Х, Ү осьтері бойынша периодты түрде қайталанып орын ауыстырады. Сөйтіп, M, N нүктелері О нүктесінің маңында Х, Ү осьтері бойымен тербелмелі қозғалыс жасайды. Олай болса, M және N нүктелерінің уақытқа байланысты ауытқуы (1.1) формулалар бойынша анықталады, яғни 1-суретте көрсетілгендей, бұл формулаларды мына түрде жазуға болады:
OM = x = Acosφ = Acosωt
OMN = y = Asinφ = Asinωt (1.2)
Егер t = 0 мезетте тербелістегі нүкте өзінің тепе-теңдік қалпында болмаса, онда оның алғашқы фазасы (φ0) туралы сөз болады. Сонда соңғы теңдеулер (1.1) формулаға ұқсас болып шығады.
Сонымен, егер нүкте шеңбер бойымен бірқалыпты айналмалы қозғалатын болса, онда оның диаметрге түсірілген проекциялары сол диаметр бойымен гармоникалық тербелмелі қозғалыс жасайды. Бұл айтылған пікір гармоникалық тербелмелі қозғалыстың кинематикалық анықтамасын сипаттайды.
Тербелістегі нүктенің тепе-теңдік қалпынан ең үлкен ауытқуын оның (А) амплитудасы деп атайды. Ал тербеліс периодына кері шама ν тербеліс периодының жиілігі делінеді. Бұл шама бірлік уақыт ішіндегі тербеліс санын көрсетедеі. Егер нүкте шеңберді толық бір айналып шықса, онда φ=2PI, олай болса бұрыштық жылдамдық мына түрде жазылады:
ω=2PIT=2PIν,
Өйткені ν=1Т тең. Сонымен (1.1) формуладағы А-тербелістегі нүктенің амплитудасы, ωt+φ0-оның фазасы. Ал φ0-тербелістің алғашқы фазасы.
Енді гармоникалық тербелмелі қозғалыс жасайтын нүктенің жылдамдығы мен үдеуін анықтайық. Ол үшін ϑ=dxdt ;2yt a=dϑdt ескеріп, (1.1) формуланы жазайық:
ϑ=dxdt=Aωcosωt+φ0=2PITAcosωt+φ0;
a=dϑdt=-Aω2sinωt+φ0=ω2x=-4PIT2x. (1.3)

(1.3) формуладағы (-) таңбасы үдеудің ауытқу бағытына қарама-қарсы екендігін көрсетеді.
Сөйтіп, гармоникалық тербелістегі нүктенің жылдамдығы тепе-теңдік қалыптың маңында, ал үдеуі ауытқудың шеткі мәндерінде максимум мәніне ие болады.
Енді нүктенің қандай күштің әсерінен гармоникалық тербеліске келетіндігін табайық. Ньютонның екінші заңы бойынша F=ma. (1.3) формуланы пайдаланып бұл теңдікті былай жазайық:
F= - mAω2sinωt+φ0= - ma2x.
Бұдан тербелістегі нүктеге әсер етуші күш оның ауытқу шамасына тура пропорционал және әрдайым тепе-теңдік қалыпқа қарай бағытталатындығы анықталады. Сондықтан мұндай күшті қайтарушы күш деп атайды. Олай болса, күштің периоды мен фазасы үдеудің периоды мен фазасына дәл келіп отырады.
Мысал ретінде серпімді күштерді, яғни Гук заңын алайық:
F= -kx,
мұндағы: k= ma2-қа тең.
Егер тербеліс х осінің бойымен түзусызықты болады десек, онда үдеу a=d2xdt2болар еді. Сонда Ньютонның екінші заңы бойынша:
md2xdt2= - kx; m=d2xdt2+kx=0. (1.4)
Осы формула гармоникалық тербелмелі қозғалыстың дифференциал теңдеуі деп аталады.
Сонымен, гармоникалық тербеліске мынадай динамикалық анықтама беруге болады. Нүктенің гармоникалық тербелісі деп ауытқу шамасында тербелетін және тербелістің орташа мәніне қарай бағытталған тербелісті айтамыз.

§ 1.2. Еркін өшетін механикалық тербелістер
Барлық реалды тербелістегі жүйелер диссипативті болып табылады Мұндай жүйенің тербелісінің механикалық энергиясы үйкеліс күшіне қарсы жұмыс істеуге жұмсалатындықтан, еркін тербелістер амплитудалары ары біртіндеп кеміп, өшеді. Бұл құбылыстарды айналу осінің екі ұшына жіп оралған Д. Максвелл маятнигімен тәжірибе жасау арқылы байқауға болады (2-сурет)

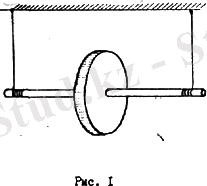
2-сурет. Максвелл маятнигі
Ауырлық күшінің әсерінен Д.Максвелл маятнигі тік вертикаль бағытта өзінің осімен айналу тербелістерін жасайды. Маятниктің осін жіпке орау арқылы H биіктікке көтеріп, оған mgH потенциалдық энергия берейік. Маятник алғашқы тепе-теңдік күйіне жеткенде потенциалдық энергия толық кинетикалық энергияға айналады. Маятник тоқтап қалмай қайтадан айналу осіне жіпті орап көтеріле бастайды (кинетикалық энергиия потенциалдық энергияға алмасады). Бірақ жіппен айналу осінің арасындағы пайда болатын үйкеліс және ауаның кедергі күшінің әсерінен, маятник бастапқы биіктігінен кіші биіктікке көтеріледі (энергияның бір бөлігі үйкеліс және кедергі күштерін жеңуге жұмсалады). Осылайша маятник амплитудалары кеміп отыратын бірнеше тербелістер жасап, тепе-теңдік орнында тоқтайды. Көптеген жағдайларда (құрғақ үйкеліс жоқ болғанда) үлкен емес жылдамдықтарда механикалық тербелістерді өшіретін күш дененің жылдамдығына пропорционал болатындығы тәжірибе жүзінде дәлелденген, Бұл күшті оның табиғатына байланыссыз үйкеліс күші деп атайық:
Fуй=-rϑ (2.1)
Мұндағы, r - кедергінің коэффициенті, ϑ - дененің жылдамдығы. Теріс таңба үйкеліс күші әрқашан қозғалысқа қарсы бағытталдығын көрсееді. ОХ осінің бойымен тербелетін сызықты өшетін тербеліс үшін Ньютонның екінші заңын жазайық:
max=-kx-rϑx (2.2)
Мұндағы, m - тербелістегі дененің массасы, ϑx және ax жылдамдық пен үдеудің ОХ осіндегі проекциялары, -kx,rϑx, қайтарушы және үйкеліс күштерінің ОХ осіндегі проекциялары.
U. = dxdt , ax=d2xdt2, шамаларын (2.2) теңдігіне қойып, түрлендірген соң мына теңдеуді аламыз:
md2xdt2+rdxdt+kx=0 (2.3)
m массасы , r кедергі және k серпімділік коэффициентін тербелістегі жүйенің параметрлері деп атайды. Егер болса r2m=km (2.3) дифференциалды теңдеуін шешудің нәтижесінде орын ауыстырудың уақытқа тәуелділік заңы шығады:
x=A0er2mtsin⁡(wt+φ0) (2.4)
Мұндағы, е-натурал логарифмнің негізі:
A=A0er2mt (2.5)
өрнегі өшетін тербелістің амплитудасы.
Өшетін тербелістердің амплитудасы уақыт өтуіне байланысты кедер коэффициенті артқан, ал массасы азайған сайын (жүйенің инерттілік кемігенде) жылдам кемиді:
ω=ω02-(r2m)2 (2.6)
шамасы диссипативті жүйенің меншікті циклдік жиілігі, ω0=km үйкеліс күшін ескермегендегі, жүйенің еркін өшпейтін тербелісінің меншікт жиілігі. t және t+T уақыт мезетіндегі өшетін тербелістердің амплитудаларының қатынасын табайық. Т - тербеліс периоды.
Өшетін тербелістер периодты емес, өйткені оларда орын ауыстырудың жылдамдықтың, үдеудің максимал мәндері ешқашан қайталанбайды. Сондықтан ω шамасы,PI секундта тербелістегі жүйе қанша рет тепе-теңдік күйден өтетіндігін көрсетсе ғана, оны шартты түрде өшетін тербелістің цикльдік жиілігі ретінде қарастыра аламыз. Сондықтан
T=2PIω=2PIω2-(r2m)2 (2.7)
шамасын өшетін тербелістің периоды, дәлірек айтсақ, өшетін тербелістің шартты периоды деп атайды. Өшетербелістердің t және t+T уақыт мезетіндегі амплитуданың қатынастарын анықтайық:
AnAn+1=A0e-r2mtA0e-r2m(t+T)=er2mT (2.8)
немесе
AnAn+1=eβT (2.9)
Мұндағы,β=r2m өшу коэффициенті деп аталады.
Т уақыт аралығында бірінен соң бірі келетін амплитудалардың орын уыстыруларының қатынастарының натурал логорифмін өшудің логарифмдік декременті деп атайды:
δ=lnAnAn+1=βT (2.10)
β және δ шамаларының физикалық мағынасын түсіндіру мақсатында τ арқылы тербелістің амплитудасы е есе кемитін уақытты белгілейік:
A0Ar=eβτ=e
Бұдан βτ =1 немесе β=1τ қатынасы шығады. Олай болса βамплитуда е есе кемитін, τ уақыт аралығына кері физикалық шама.
β=102c-1 теңдігі тербеліс амплитудасы 10[-2] с уақытта е есе кемитіндігін көрсетеді. N рет тербеліс жасағанда амплитуда е есе кемісе, мына қатынастар алынады:
τ=N∙T , δ=βT=Tτ=1N
τ - релаксация уақыты. Өшудің логарифмдік декременті N тербеліс жасағанда, амплитудасы е есе кемитін тербеліс санына кері физикалық шама. Мысалы, δ = 0,01 мәні 100 рет тербелгенде амплитуда е есе кемитіндігін көрсетеді. Егер тербелістің өшу коэффициенті онша үлкен болмаса, онда ол шартты алынған периодқа әсерін тигізбейді (3-сурет).

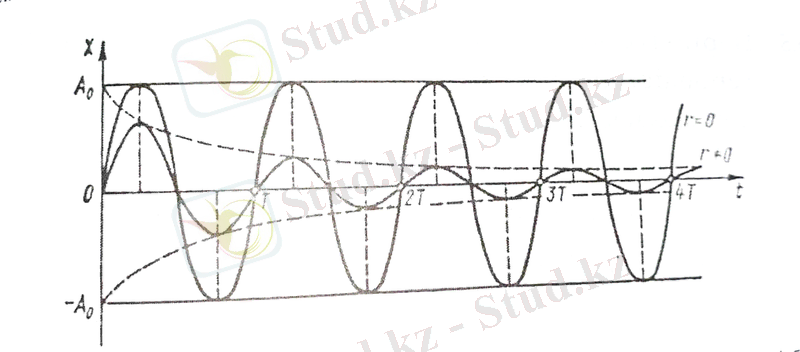
3-сурет.Тербелістің өшу коэффиценті үлкен болмаса,периодқа әсерін тигізбейді.
Егер өшу коэффициенті үлкен болса, амплитуда жылдам кеміп, тербеліс периоды артады. Кедергі критикалық мәнге тең болғанда, яғни:
r=rk=2mω0 немесе β=ω0
(2.6) теңдеуінен өшетін тербелістердің циклдік жиілігі айналатындығын көреміз. Олай болса, тербеліс тоқтайды. Тепе-теңдік әсер күйінен қандай да бір сыртқы күштің әсерінен ауытқыған жүйе, жойылғаннан соң апериодты түрде тепе-теңдік орныңа оралады. (4-сурет)
Тербелмелі қозғалыста жүйе тепе-теңдік күйге оралған мезетте, онда кинетикалық энергияның қоры болады. Апериодты қозғалыста тербелістегі жүйенің барлық механикалық энергиясы үйкеліс күшін жеңуге жұмсалады Үйкеліс күші өте үлкен болғанда апериодты қозғалыс баяу өтеді.

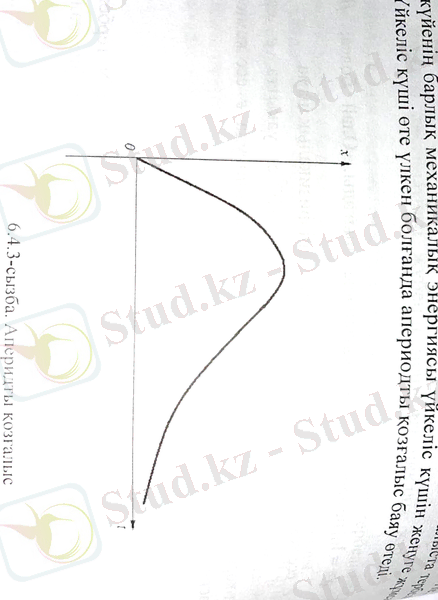
4-сурет. Апериодты қозғалыс

§ 1.3. Еріксіз механикалық тербелістер
Тербеліс жасайтын жүйеге серпімді - kx және кедергі -rϑ күштерінен басқа қосымша периодты F еріксіз күш әсер етсін делік. Мұндай тербеліст астынан жоғары қарай тең уақыт аралығында итеріліп отыратын серіппег ілінген жүк жасайды. Егер мәжбүр күштің периодты жүйенің еркін тербелісінің периодына тең болмаса, алғашқыда бірнеше соғу байқалып, содан соң амплитудасы тұрақты тербеліс орнығады.

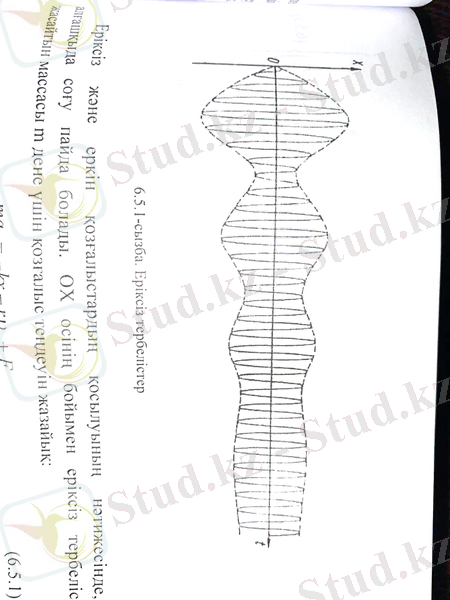
5-сурет. Еріксіз тербелістер
Еріксіз және еркін қозғалыстардың қосылуының нәтижесінде, соғу пайда болады. ОХ осінің бойымен еріксіз тербеліс массасы т дене үшін қозғалыс теңдеуін жазайық:
mах=-kx-rϑx+Fx (3.1)
Мұндағы, Fх - периодты әсер ететін F мәжбүр күштің ОХ осіндегі құраушысы.
(3.1) теңдеуіндегі жылдамдық пен үдеуді орын ауыстырудың уақыт бойынша бірінші және екінші туындылары арқылы өрнектеп, төмендегі еркекті аламыз:
md2xdt2+rdxdt+kx=Fx (3.2)
Мәжбүрлейтін күш гармоникалық заңмен өзгеретін қарапайым қарастырайық:
Fx=F0cosωt (3.3
F күшінің әсерінен пайда болған жүйенің еріксіз тербелісін гармоникалық, ал циклдік жиіліктерін тең деп алып, тербелістің А амплитудасы мен бастапқы фазасын φқ анықтайық:
x=Asin(ωt+φ0) (3.4)
өрнегінен жылдамдық пен үдеуді табамыз:
ϑx=dxdt=ddtAsinωt+φ0=Aωcos⁡(ωt+φ0)
ax=dϑdt=ddtA cosωt+φ0=-Aω2sinωt+φ0=Aω2cos⁡(ωt+φ0 +PI2)
x=Acos⁡(ωt+φ0-PI2)
Осы өрнектерді (3.2) теңдігіне қойып,мына теңдеуді аламыз:
mAω2cosωt+φ0+PI2+rAωcosωt+φ0+kA2cos ωt+φ0-PI2=FmAcosωt
Теңдіктің барлық мүшелерін mA бөлейік:
ω2cosωt+φ0+PI2+rmωcosωt+φ0+kmcos(ωt +φ0-PI2)=F0mAcosωt (3.5)
km=ω02 және r2m=β ескерсек, (3.5) теңдігінен төмендегі өрнек шығады:
А1cosωt+φ0+PI2+А2cosωt+φ0+A3cosωt+φ 0-PI2=A4cosωt (3.6)
Мұндағы, A1=ω2, A2=2ωβ, A3=ω03 , A4=F0mA (3.7)
(3.6) теңдігінің оң жағын үш гармоникалық тербелістің қосындысынан алынған гармоникалық тербеліс ретінде қарастыруға болады. Тербелістерді қосу үшін векторлық диаграмма әдісін пайдаланамыз. ОХ түзуін жүргізіп,
A4=A1+A2+А3 болатындай етіп төрт векторды ОХ түзуімен бастапқы фазаларына сәйкес келетін бұрыштармен орналастырайық.
6-суреттен A42=(A3-A1)2+A22 теңдігі шығады.
(3.7) қатынастарын пайдалансақ, амплитуда мынаған тең болады:
A=F0m(ω02-ω2)2+4β2ω2 (3.8)

6-сурет. Векторлық диаграмма
Орныққан еріксіз тербелістердің амплитудасы мәжбүрлейтін күштің F0, амплитудасын тура, жүйенің массасына кері пропорционал. Өшу коэффициенті артқан сайын тербелістің амплитудасы кемиді. F0, m, β тұрақты болса, амплитуда жүйедегі мәжбүрлеуші күштің (ω) және өшпейтін еркін тербелістердің (ω0) жиіліктерінің арақатынасына тәуелді. 6-сурет орнықталған еріксіз тербелістің жылдамдығы мен күш арасындағы φ0 фазаның ығысуын және орын ауыстыруы мен мәжбүрлеуші күш арасындағы ығысу фазаларын анықтауға мүмкіндік береді:
tgφ0=A3-A1A2=ω02-ω22βω (3.9)

tga=-2βωω02-ω2 (3.10)
(3.8) өрнегін зерттеп, еріксіз тербеліс амплитудасының мәжбүрлеуші күштің циклдік жиілігіне тәуелділік графигін саламыз. (7-сурет)
а. Мәжбүрлеуші күштің циклдік жиілігі ω = 0 болған жағдайда тербеліс болмайды. Еріксіз тербелістегі орын ауыстыру F0 тұрақты күш әсер сткендегі статикалық деформацияға тең.

7-сурет. Амплитуданың циклдік жиілікке тәуелділік графигі
x=A0=F0mω02=F0k
Сондықтан А0, ауытқуын статикалық амплитуда деп атайды.
ә. Егер өшу жоқ болса, (β1=r2m=0)мәжбүрлеуші F күштің жиілігі өсіп, ω=ω0 болғанда шексіз үлкен мәнді иеленіп, қайтадан кеми бастайды.[limn--infinityA=0]
б. Егер өшу бар болса, (3.8) теңдеуінің оң бөлігі минимумға жеткенде, амплитуда максимал мәнді иеленеді. Түбір астындағы өрнектің бойынша алынған бірінші туындыны нөлге теңестіріп, минимум шарты аламыз:
-4ω02-ωрез2+8β2ωрез=0 (3.11)
Мұндағы, ωрез, A=Amax болғандағы мәжбүрлеуші F күштің циклдік жиілігі. (3.11) өрнегін түрлендірсек, мына теңдік шығады:
ωрез=ω02-2β2=ω01-2β2ω02 (3.12)
ω0 циклдік жиілікті резонанстық, ал еріксіз тербелістің амплитудасының артып, мәжбүрлеуші күштің циклдік жиілігінің ωрез мәніне жақындауын резонанстық құбылыс деп атайды.
(3.12) формуласынан консервативті жүйе үшін ( β=0) ωрез=ω0, ал диссипативті жүйеде ωрез меншікті циклдік жиіліктен ω=ω02-β2 запасы кіші екендігін көреміз. Өшу коэффициенті артқан сайын, резонанс обылысы әлсіз байқалып, β=ω02 болғанда жойылады. Резонанс обылысы радиотехникада (радиоқабылдағышты белгілі радиостанцияның киілігіне келтіру), акустикада (дыбыстарды талдау, оларды күшейту, т.б.) жиі қолданылады. Сонымен қатар периодты күштер әсер ететін әртүрлі құбылыстар мен машиналар үшін резонанс құбылысы өте қауіпті. Мысалы, машинаның айналатын бөліктері, турбина валдары, ұшақтың винттері абсолют дәл тепе-теңдік күйде болмағандықтан (олардың массалар центрі айналу осімен салыстырғанда сәл ауытқыған), оларға айнымалы күш әсер етіп, еріксіз тербеліс жасайды. Айнымалы күштер әсер ететін құбылыстар мен қондырғыларды жобалағанда міндетті түрде арнайы есептеулер арқылы резонанс құбылысының пайда болуына кедергі жасалады.
Өшетін тербелістерде жүйенің энергиясы ортаның кедергісін жеңуге жұмсалады. Егер осы кеміген энергияны толықтырып отырсақ, тербеліс ішпейді. Жүйенің энергиясын толықтыру сырттан әсер ету арқылы іске асырылады. Бірақ әсер жүйеге оның тербелісімен бағыттас бірдей жиілікпен берілуі қажет. Бұл шарт орындалмаса, тербеліс әлсірейді немесе мүлдем тоқтайды. Тербелісі бастапқы сілкіністен немесе периодты әсер күшінен туындайтын, сырттан келетін энергияның салдарынан пайда болатын және жергияны өзі реттейтін жүйе автотербелістегі жүйе деп аталады. Автотербелетін жүйеге сағат механизмін жатқызуға болады. Авто- тербелістердің жиілігі және амплитудасы жүйенің қасиеттерімен анықта- лады. Қарапайым автотербелістегі жүйенің өзі күрделі теңдеулермен сипатталады.
Өшетін гармониялық тербелістер. Еріксіз тербелістер. Резонанс
Енді бірі t уақыт мезетінде тербеліс периоды Т-ға артады деп есептеп, амплитудасын салыстыратын болсақ, онда берілген тербеліс үшін AtAt+T=ebT2m=const болатындығын байқаймыз.

Сонда мына формула: δ=lnebT2m=bT2m

8-сурет. 9-сурет.
шамасы өшетін тербелістің логарифмдік декременті деп аталады да, ал тербелістің өшу тездігін сипаттайды.
Еріксіз тербелістер. Резонанс. Үздіксіз өшпейтін тербеліс болу үшін кедергі күшін жеңе отырып, тербелуші денені қосымша күш арқылы қозғалысқа келтіру қажет. Себебі әсер етуші күштің нәтижесінде істелінген жұмыс кедергіні жеңуге кеткен энергия қорын толтырып отырады.
Ньютонның екінші заңының еріксіз тербеліс күшін былай жазуға болады:
md2xdt2=-kx-bdxdt+F0sinωt
мұндағы: kx - қайтарушы күш, -bdxdt - ортаның кедергі күші. Бұл теңдікті өзгертіп жазсақ, онда:
md2xdt2=+kx+bdxdt+F0sinωt
Бұл формула еріксіз тербелістің дифференциал теңдеуі деп аталады. Теңдеуді шешсек, онда ауытқудың уақытқа байланысын былай өрнектеуге болады:
x=Asin(ωt+φ0)

10-сурет.
Еріксіз тербелістің амплитудасы:
A=F0mω02+ω2+bm2ω2,
Алғашқы фазасы: tgφ=-bm(ω02+ω)
формуладан ω--ω0, онда еріксіз тербелістің амплитудасы өседі. Егер b= 0, яғни кедергі күші жоқ болса, ω=ω0, болып, A= max артып, шексіз өседі. Сөйтіп, еріксіз тербеліс кезінде , ω=ω0, , болады, амплитуданың артуы резонанс құбылысы деп аталады да, оның графигі былай кескінделеді. (10-сурет)

§ 1.4. Параметрлік тербелістер
Өзара перпендикуляр гармониялық тербелістерді қосу.
Егер периодтары бірдей өзара перпендикуляр гармоникалық тербелістерді қосу керек болса, онда олардың теңдеуі мына түрде беріледі:

x=A1sinωt+φ1 (4.1)
x=A2sin⁡(ωt+φ2)
мұндай тербелістерді қосқанда олар қалай қозғалады және траекторияларының түрлері қалай өзгереді, соны қарастырайық.

11-сурет.
Сонда қорытқы тербелістің траекториясы қабырғалары 2A1 және 2А2, тең тік төртбұрыштың ішінде қатады (11-сурет). Ол үшін (4.1) теңдеулер жүйесіндегі уақыттан құтылуымыз керек. Сондықтан бірнеше дербес жағдайды қарастырайық:
Фазалар айырымы φ1-φ2=0 болсын. Енді(4.1) теңдеулердің бірін-біріне өзара мүшелеп бөлейік:
xy=A1A2
бұдан
y=A2A1x (4.2)
Бұл түзудің тіктөртбұрыштың І және II ширегінде жататын траекториясы (11-сурет).
Фазалар айырымы φ1-φ2=PI тең болсын. Бұдан φ1=φ2+PI болса, онда (4.1) теңдеулердің біріншісін былай жазамыз:
x=A1sinωt+PI+φ2=-A1sinωt+φ2.
Енді (4.1) теңдеулерді жоғарыдағыдай мүшелеп бөлсек:
y=-A2A1x (4.2а)
ал бұл түзудің тік төртбұрыштың II және IV ширегінде жататын траекториясы болады (11-сурет).
Енді осы екі түрлі жағдай үшін тербелістегі нүктенің координаттар бас нүктесінен қандай қашықтықта болатынын уақыттың функциясы ретінде көрсетейік. Пифагор теоремасы бойынша:
z2=x2+y2=A12+A22sin2ωt+φ2,
немесе
z=A12+A22sin2ωt+φ2,
Міне, осы өрнек нүктенің гармоникалық тербелісінің теңдеуі деп аталады.
Сонымен, құраушы тербелістер фазаларының айырымы 0-ге немесе 2PI-ге тең болса, онда периодты құраушы тербелістегідей сол түзудің бойымен бағытталған және амплитудасы А-ға тең гармоникалық тербеліс қорытқы тербеліс болады. Сонда:
A=A12+A22
Фазалардың айырымы φ1-φ2=PI2 болсын, онда φ1=φ2-PI2 сөйтіп (4.1) теңдеулердің біріншісін мына түрде жазайық:
tx=A1sinωt+PI2+φ2=A1cos.
(4.1) теңдеулер жүйесінің біріншісін А1 , екіншісін А2 - ге бөлейік:
xA1=cos⁡(ωt+φ1)
xA1=sin⁡(ωt+φ1)
Енді осы теңдеулер жүйесінен екі жағын квадраттасақ,онда:
x2A2=cos⁡2(ωt+φ1)
y2A22=sin2(ωt+φ2)
Мұндағы cos2ωt+φ1+sin2ωt+φ2=1 екендігін ескерсек және теңдеулердің сол жақтарын қоссақ, мынау шығады:
x2A12+y2A22=1 (4.3)
Бұл өрнек эллипс теңдеуі. Олай болса, тербелістегі нүктенің тік төртбұрыш ішіндегі траекториясы эллипс екен.

ІІ ТАРАУ. МАТЕМАТИКАЛЫҚ МАЯТНИК ТЕРБЕЛІСТЕРІН МАТЕМАТИКАЛЫҚ МОДЕЛЬДЕУ
§ 2.1. Математикалық модель туралы
Осыдан 400 жылдай бұрын табиғатты зерттеуші ғалым Галилео Галилей математиканың барлық ғылымдардың ортақ тілі екендігін ерекше атап көрсеткен, сөйтіп Философия ұланғайыр кітапта - ұлы Табиғатта жазылған дүние, оның беттері әрқашан және әркімге де ашық. Бірақ оны, оның тілін және жазылған таңба-символдарын меңгерген адам ғана түсіне алады. Бұл ұлы кітап математика тілінде жазылған, ал оның таңбалары - математикалық формулалар - деген болатын. Оның ғасырлар асып бізге жеткен бұл көрегендігін кейінде басқа көптеген ғалымдар да растады.
Математика әрқашан дүниетанудың сапалық жақтарын зерттейтін физика, химия, биология, астрономия сияқты ғылымдардың күнделікті қолданатын зерттеу құралына айналғаны қазіргі кезде еш дау тудырмас ақиқатқа айналып отыр.
Көптеген табиғат құбылыстары мен өндірістің процестерін түсіну және келешекте оларды сапалы түрде басқаруға қол жеткізу мақсатында біз оларды математикалық модельдеуге көштік. Алғашында қолда бар қарапайым процестерді зерттеуден басталған бұл математикалық мольдеу, қазіргі таңда өте-мөте күрделі құбылыстарды да сипаттап бере алатындай, жоғары деңгейге көтерілді.
Зерттеу методы ретінде модельдеу әдісі бізге ертеден, сонау Леонардо да Винчи мен Галилейлер заманынан белгілі. Модельдеу әдістері эксперименттік зерттеулер мен теориялық ізденістерге, нақты техникалық жобалар жасауда неме өте абстрактілі логикалық схемалар құруда және тағы басқа жерлерде қолданылады.
біМодельдеудің бірнеше түрі бар: материалдық (заттық) және идеалдық модельдеу. Материалдық модельдеудің негізгі түрлері ретінде физикалық және аналогиялық модельдеуді айтамыз.
Физикалық модельдеу деп объектінің өзіне оның үлкейтілген немесе кішірейтілген көшірмесін сәйкес қою арқылы модельдеуді айтамыз. Физикалық модельдеуге мысалдар: астрономияда - планетарий; гидротехникада - суы бар науа; модельденген өзендер мен тоспалар; сәулет өнерінде - ғимараттар макеті; ұшақ құрастыруда - ұшу аппаратының модельдері және т.б.
Аналогиялық модельдеу физикалық табиғаты әртүрлі, бірақ формальды түрде бірдей математикалық теңдеулермен , логикалық схемалармен және т.б. сипатталатын процестер мен құбылыстардың ұқсастығына негізделген. Бұл модельдеудің қарапайым мысалы - механикалық тербелістерді бірдей дифференциал теңдеулермен өрнектелетін электр схемасы көмегімен оқыту.
Материалдық модельдеудің бұл екі түрі де негізгі объектінің материаолдық бейнесі (кескіні) және оның басқа да сипаттамаларымен тығыз байланыста болады. Сондықтан материалдық модельдеу өзінің табиғатында экспериментальдық метод болып табылады.
Идеалдық модельдеудің материалдық модельдеуден айырмашылығы - мұндағы әрекеттер идеалдық сипатта, яғни ойдағы қияли аналогия негізінде іске асады. Идеалдық модельдеудің мазмұны теориялық сипатта болады,оның екі нұсқасы бар: интуитивтік және таңбалық. Модельдеудің интуитивтік түрінде зерттеу объектісі жайында мәлімет интуитивтік түсінікте негізделеді. Мысалы, әрбір адамның өмірлік тәжірибесі оның қоршаған орта туралы интуитивтік моделі болып табылады. Таңбалық модельдеуде модель ретінде қандай да бір түрдегі таңбалық түрлендірулерді, схемаларды, графиктерді, сызбаларды, формулаларды, символдар жиынын және т.б. алады. Таңбалық модельдеудің басты түрі математикалық модельдеу болып табылады.
Модель, модельдеу, оның көрнекілігі деген ұғымдар ұдайы өзгеріс тауып, кеңейіп кетеді. Мысалы, ХІХ ғасырда атақты ғалым Кельвиннің айтқанымен механикалық моделін көзіме елестетпейінше ешқандай құбылысты түсіне алмаймын - деген сөзінің мағынасы зор. Қазір де біз қандай болмасын бір құбылысты не өндіріс процесін модельдегенде электрлік, логикалық схемаларды не басқа да математикалық формулаларды пайдаланамыз.
Математиканың барлық дерлік ғылымдар үшін ортақ тіл, ортақ зерттеу аппаратына айналғандығы ежелден бері белгілі. Соның бір дәлелі болса керек, ежелгі гректер Геометрияны білмеген адам Философиямен айналысуға құқы жоқ деген. Ғылыми зерттеулерге қойылатын қатаң талапты кезінде Леонардо да Винчи былайша тұжырымдаған: Ешбір зерттеу нәтижесі математикалық дәлелдеу тезінен өтпейінше шынайы ғылым бола алмайды.
Енді математикалық модельдеу деген не, соған тоқталайық. Табиғаттың кез-келген құбылысын қандай да бір материалдық системаның өзгеруі деп түсінген жөн. Осындай әрбір өзгеріске сәйкес нақты бір процесс жүреді, ал оның барысында осы системаның қалып-жағдайын сипаттайтын айнымалы шамалар өзгеріске ұшырап отырады. Бұл шамаларды режим параметрлері деп атайды. Егер нақты бір құбылысты (процесті) анықтайтын параметрлер жиынтығы үшін оның математикалық сипаттаушы өрнегі белгілі болса, онда осы құбылыстың (процестің) ұқсастық критерийлері де табылады, сөйтіп осы құбылыстың математикалық моделі болып табылатын қандай да бір теңдеулер не қатыстар алынады. Объектіні зерттеу әртүрлі математикалық методтарды пайдалану нәтижесінде құрылған математикалық модель арқылы жүргізіледі. Модельдеу арқылы қазіргі кезде түрліше күрделі техникалық агрегаттардың: бу қазандары мен турбиналардың, атомдық станциядағы ректорлар мен сұйық металдарды айдайтын насостардың, вентиляциялық қондырғылардың және тағы басқалардың жұмыстарын алдын-ала зерттеуге болады. Электронды есептеу техникасының (ЭЕТ) соңғы кездері жедел қарқынмен дамуына байланысты, математикалық модельдеу әдісі өте қуатты зерттеу методына айналып отыр. Бұрындары әліміз келмеген көптеген есептерді зерттеп шешу мүмкіндігі пайда болды. Дәл қәзіргі кезеңде математикалық модельдеу, зерттеушінің - адамның таланты мен тәжірибесіне негізделген эвристикалық әдістермен толыға келе, имитациялық математикалық модельдеу дегенге айналып отыр. Математикалық модельдеудің классикалық бір мысалы ретінде механикадағы Ньютон заңдарының өздерімізге мектептен белгілі формулалармен берілуін атауға болады.
Қазіргі кезде ғылыми және педагогикалық зерттеу жүргізуде, яғни зерттеу объектілерін оқып-үйренуде, оларды біліп-тану үрдісінде математикалық модельдерді қолданудың ролі артып отыр. Табиғаттағы шындық процестердің сызықтық емес жүйелерін модельдеу арқылы ақиқатты тану, таным үрдісінің кеңеюіне және білім берудің артуына мүмкіндік береді.
Ендігі сұрақ: Модельдік зерттеулер қалай жүргізіледі? Ең алдымен зерттеудің бастауы ретінде тиісті салада (физика, химия, биология, экономика және басқалардан) туындаған белгілі бір есеп алынады. Осы есепке математикалық модель құрылады. Одан арғы жерде осы модельді таңдау үшін құрылған алгоритм пайдаланылады. Егер модель мен алгоритм соншалықты күрделі болмаса, онда модельді қолма - қол аналитикалық жолмен зерттеуге болады. Кері жағдайда, алгоритмді ЭЕМ-да орындайтындай бағдарлама құрылады. Одан арғы жерде осы модельді таңдау үшін құрылған алгоритм пайдаланылады. Егер модель мен алгоритм соншалықты күрделі болмаса, онда модельді қолма - қол аналитикалық жолмен зерттеуге болады. Кері жағдайда, алгоритмді ЭЕМ-да жүргізілген есептеулердің нәтижелерін сәйкес саладан алынған нақты тұжырымдармен салыстырамыз. Егер есептеулер нәтижесі тиісті есепке сәйкес келмесе, онда құрылған модельге қайта ораламыз ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.