Математикалық индукция әдісі

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 50 бет
Таңдаулыға:

Қазақстан Республикасы Білім және ғылым министрлігі

Л. Н. Гумилев атындағы Еуразия ұлттық университеті

Оспанова Ганзира Айтхожаевна

ОҚУШЫЛАРДЫҢ ЖАС ЕРЕКШЕЛІКТЕРІН ЕСКЕРЕ ОТЫРЫП,

«МАТЕМАТИКАЛЫҚ ИНДУКЦИЯ ӘДІСІ» ТАҚЫРЫБЫН БЕРУДІҢ ЖАҢА ӘДІСТЕМЕСІ

6М010900 - Математика мамандығы

бойынша математика магистрі академиялық

дәрежесін алуға магистрлік диссертация

(ғылыми - педагогикалық бағыт)

Нұр - Сұлтан 2020

Қазақстан Республикасы Білім және ғылым министрлігі

Л. Н. Гумилев атындағы Еуразия ұлттық университеті

«Қорғауға жіберілді»

Механика -математика

факультетінің деканы,

PhD докторы

Д. Х. Қозыбаев

«__»2020ж

Магистрлік диссертация

Тақырыбы: «Оқушылардың жас ерекшеліктерін ескере отырып,

« Математикалық индукция әдісі » тақырыбын берудің жаңа әдістемесі»

6М010900 - «Математика» мамандығы бойынша

(ғылыми - педагогикалық зерттеу)

Магистрант: Г. А. Оспанова

Ғылыми жетекшісі

PhD Ғ. Е. Тауғынбаева

Кафедра меңгерушісі

PhD Р. Ж. Наурызбаев

Нұр - Сұлтан 2020

Мазмұны

КІРІСПЕ . . . 4

І. ОРТА МЕКТЕПТЕГІ МАТЕМАТИКА ПӘНІ ОҚУЛЫҚТАРЫНДАҒЫ «МАТЕМАТИКАЛЫҚ ИНДУКЦИЯ» ТАҚЫРЫБЫНА ШОЛУ ЖӘНЕ АНАЛИЗ . . . 6

Қазақстан Республикасында орта мектептерде қолданыста болған

және қолданыстағы оқулықтарындағы «Математикалық индукция»

тақырыбына шолу және оларға анализ . . . 6

Ресей орта мектептерде қолданыста болған және қолданыстағы

оқулықтарындағы «Математикалық индукция» тақырыбына шолу және

оларға анализ . . . 9

Шетел мектептерінде қолданыста болған және қолданыстағы

оқулықтарындағы «Математикалық индукция» тақырыбына шолу және

оларға анализ . . . 12

ІІ МАТЕМАТИКАЛЫҚ ИНДУКЦИЯ ӘДІСІН МЕКТЕПТЕ БЕРУ

2. 1. Математикалық индукция әдісінің берілу тарихы . . . 17

2. 2. 2019-2020жылдары математикалық индукция әдісі қай сыныптарда

қанша сағат берілді . . . 24

2. 3. Математикалық индукция әдісі Н. Н. Темірғалиевтің беруі . . . 28

2. 4. Факультатив сабақ (34 сабақ математикалық индукция жоспары,

талқылануы, материалдары) . . . 31

2. 5. Эксперимент (8, 9, 10, 11) қорытындылау . . . 54

ІІІ. Қорытынды . . . 65

Қолданылған әдебиеттер тізімі . . . 67

КІРІСПЕ

Ақыл-ойды тәртіпке келтіретін математика екенін әлімсақтан белгілі. Ал осы біздің мектептеріміздегі математика мазмұны қалай жасалуда? Қандай тақырыптарға өз деңгейінде сағаттар бөлініп, қай деңгейде оқытылып жатыр? Математикалық индукция әдісі қаншалықты керек? Оны түсіндірудің қиындықтары неде? Қоғамның өзгеруі мен дамуының осы типтес сұрақтарға берер жауабы қандай? Математикалық индукция әдісін қолданудың қандай жолдары бар? Математикалық индукция әдісін берудің жаңа қандай әдістерін ұсынған тиімді ?-деген сұрақтар ұстаздар қауымында көптеп қойылуда. Осы және де басқа сұрақтарға мейлінше дәл жауап беру үшін осы тақырыпты зерттеуді қолға алдық.

Мектепте берілетін математикалық білімніің мазмұны қоғамның дамуымен бірге заман ағымына қарай түбегейлі болмағанмен өзгеріске ұшырайтыны рас. Осы орайда ой-түйіндеу мен қорытындылау нәтижесінде қол жеткізілетін тапсырмалар мен математикалық индукция әдісімен шығарылуы әдеттегіден оңайлау есептер кездесіп тұрады. Негізінен математикалық индукция әдісін нақты 9 сыныпта қарастырғанмен жалқыдан жалпыға өту мәселесі, осы жолмен тұжырымға келу есептері одан ертерек қолға алынады.

Білім алушыларға бүгінде тек есептерді техникалық жолмен шығара беруден гөрі оларды ой-тұжырымдауға баулитын, шешім қабылдау барысында логикалық реттілікті үйрететін әдістің бірі -математикалық индукция әдісі деп білеміз. Тепе-теңдіктер мен теңсіздіктерді дәлелдеу, бөлінгіштіктің қасиеттері, геометрия есептерін шығаруда математикалық индукция әдісі есепті дұрыс шығару процесін едәуір жеңілдетеді.

Өзектілігі: Метематикалық индукция әдісін пайдаланып есептерді шығару екінің бірінің қолынан келе бермейтіні рас. Бұл салыстырмалы түрде - күрделі тақырыптардың бірі. Алайда, математикалық индукция әдісі арқылы дәләлденетін көптеген есептерді шығаруға оңайырақ жолмен жету мақсатында бұл тақырыпты меңгерудің ролі зор. Жалқыдан жалпыға өту мәселесі жасанды интеллекті дамыту мен бірге қоғам дамуына қарай ілгерілеп отырған математикалық білім мазмұнында өзінің ойып тұрып алатын орны бар екендігі ғылымның қаншалықты қарыштап даумуымен байланысты. Сондықтан да осы әдісті үйретудің бірден-бір жолы жаңа тәсілмен берудің сапалы жағын қарастыру болып табылады.

Мақсаты: Оқушылардың жас ерекшелігіне қарай математикалық білім мазмұнын жасау белгілі нәрсе болғанымен, тақырыпты беру барысында олардың психологиялық ахуалын да бақылаған дұрыс. Осы орайда математикалық индукция әдісін беруде жас ерекшелігін сақтай отырып есептерді жүйелеу, тақырыптардың күрделілігіне қарай есептер мазмұнын құрастыру сияқты нәрсеге көңіл бөлу.

Міндеттері:

Мектеп оқулықтарындағы математикалық индукция әдісіне шолу жасау,
Мектеп оқулықтарындағы математикалық индукция әдісіне анализ жасау,
Математикалық индукция әдісіне берудің әдістемесін ұсыну,
Эксперимент жасау арқылы математикалық индукция әдісін беру жас ерекшеліктерін анықтау,
Факультативтік сабақ бағдарламасын ұсыну.

1. Орта мектептегі математика пәні оқулықтарындағы «математикалық индукция» тақырыбына шолу және анализ

Қазақстан Республикасында орта мектептерде қолданыста болған және қолданыстағы оқулықтарындағы «Математикалық индукция» тақырыбына шолу және оларға анализ

Математиалық индукция әдісі мектеп математикасындағы математикалық анализді түсінуге, әрі түйсінуге бағыттайтын бірден-бір тақырып болып табылады. . Бүгінгі күнге дейін математикалық индукция тақырыбын түсінікті беру, мектеп математика оқулықтарына енгізу үшін көптеген оқулықтар мен оқу құралдары пайдалаылды.

Оқулықтардағы математикалық индукция әдісінің берілуі аясында жұмыс жасау мақсатында Отандық және Ресей оқулықтарын [1-11] және тағы басқа оқулықтар мен оқу құралдарын қарастырдым.

Ә. Н. Шыныбеков, Д. Ә. Шыныбеков, Р. Н. Жұмабаев. Жалпы білім беретін мектептің 9 сыныбына арналған «Алгебра» оқулығында математикалық индукция әдісінің анықтамасын бермес бұрын толымсыз және толық индукцияға тоқталып өткен.

Математикалық индукция анықтамасын бермес бұрын қарастырылып отырған мысалдар жүйесіздеу берілген.

Бәрін оқушы біледі деп жорамалдаған сияқты. Бұл оқушыға қиын тиеді. Математикалық индукция тақырыбындағы тапсырмалар деңгейі де бірден күрделі болып берілген.

$C:\Users\Student\AppData\Local\Packages\Microsoft.MicrosoftEdge_8wekyb3d8bbwe\TempState\Downloads\6,9 (1).PNG$

Оқулыққа көз жүгіртетін болсақ алдымен математика үшін пікір дегеніміз не?Алақай, бүгін мереке! Күн жылы ма? - осылардың барлығы пікір ма?Сол анықтамасы белгісіз пікір ақиқат дегеніміз не?

Ал осы екі қадамнан өтсек не болады? «Егер осы кезеңдердің екеуі де дәлелденсе, онда A(n) сөйлемі математикалық индукция принціпі бойынша кезкелген натурал n саны үшін орындалады.

Енді (1) теңдіктің ақиқаттығына оралайық. Дәлелдеуіміз бойынша А(1) ақиқат және А(k) -ның ақиқаттығынан A(k+1) -дің ақиқаттығына көз жеткіздік. Олай болса, теңдік кез келген натурал саны үшін орындалады. » Алайда, анықтаманы беру және мысалды көрсету бірі басында, екіншісі аяғында келгендіктен оқушы ойы шашырап өз бетінше түсінуіне мүмкіндік болмайды.

Десек те, анықтамаға дейінгі мысалдың күрделілігі анықтаманы толық түсінуге кедергі жасайды. Жалпы осы оқулықтағы тапсырмаларда да бөлінгіштік тақырыбына есептер берілмегенімен оған тақырыпты беру барысында түсіндіру мысалы қарастырылмаған.

Әбілқасымова А. Е., Кучер Т. П., Корчевский В. Е., Жумагулова З. А. Жалпы білім беретін орта мектептің 9 сынып Алгебра оқулығында математикалық индукция әдісітеорема түрінде берген де бірақ оның дәлелдеуі түсініксіз берілген. Мысалдың түрі көрсетілген де бірақ дәлелдеуі келтірілмеген.

$C:\Users\Student\AppData\Local\Packages\Microsoft.MicrosoftEdge_8wekyb3d8bbwe\TempState\Downloads\9,2 (1).PNG$

Тағы да сол қателік, тақырып тұжырым дегеннің не екенін анықтамастан, 3 мысалға сүйеніп, үшеуінде де натурал сандар қатысады делінген. Артынша, дәлелдеудің бір түрі - математикалық индукция әдісін теорема арқылы берген. Теоремада A(n) тұжырымын да солай натурал санды қамтитын деп алып, екі қадамнан кейін ол кез келген натурал сан үшін орындалатындығын айтады. Мысалдарды бергенімен де шығару жолы оқулықта түсіндірілмеген.

9сыныпқа арналған Г. Н. Солтан, А. Е. Солтан, А. Ж. Жумадилованың «Алгебра» оқулығы, бұл оқулықта математикалық индукция әдісін аксиома негізінде берген. Бірақ анықтаманы бермес бұрын натурал сандар негізінде мысал дәледенбеген. Бірден тұжырым туралы айтылады да, оған түсінік кейін беріледі. Бұл оқулықта да берілген қателіктер жоғарыдағыдай.

Оқулықта тапсырмалар іріктеліп, математикалық индукцияны пайдаланып дәлелдейтін көптеген мысалдар мен есептер берілген. Бірақ толымсыз, толық индукциялар туралы жақ ашпапты. Тақырып толық емес, тек ойып алынған деңгейде берілген. Жүйе жетіспейді.

Келесі оқулық Н. Т. Темірғалиевтың, Б. Әубәкір, Е. Баилов, М. К. Потапов, 10 сыныпқа арналған Алгебра және анализ бастамалары оқулығында математикалық индукция тақырыбы өте жақсы берілген. Оқулық жоба түрінде болғанымен математикалық индукция әдісі өте сауатты берілген. Тақырып ты түсіндіру барысында анықтамаға дейін пікір ұғымын жақсылап бекіткендіктен анықтама мейлінше түсінікті.

Теориясы да мысалдармен астасып, жүйелі түрде берілген. Меніңше осы оқулықтағы математикалық индукция тақырыбының берілуі ең жүйелісі сияқты.

А. Е. Әбылқасымова, Н. Р. Майкотов, Қ. А. Қаңлыбаев, Ә. С. Кенеш, жалпыбілім беретін мектептің 9 сыныбына арналған Алгебра оқулығында математикалық индукция тақырыбы прогрессиялардан соң берілген. Математикалық индукция әдісін беруде натурал сандарға тоқталып барып берген.

Алайда, математикалық индукцияның анықтамасын бергенде дерексіздік орын алатын сияқты, яғни n=n ₀ , болған жағдайдың өзі оқушыға түсінуіне қиындық туғызары анық. Тақырыпты бекітуге берілген есептер әртүрлі болғанымен деңгейленуі дұрыс емес. Бірді айтып бірге кеткен сияқты, немесе әр тақырыптан жүйесіз жиналған есептер сияқты.

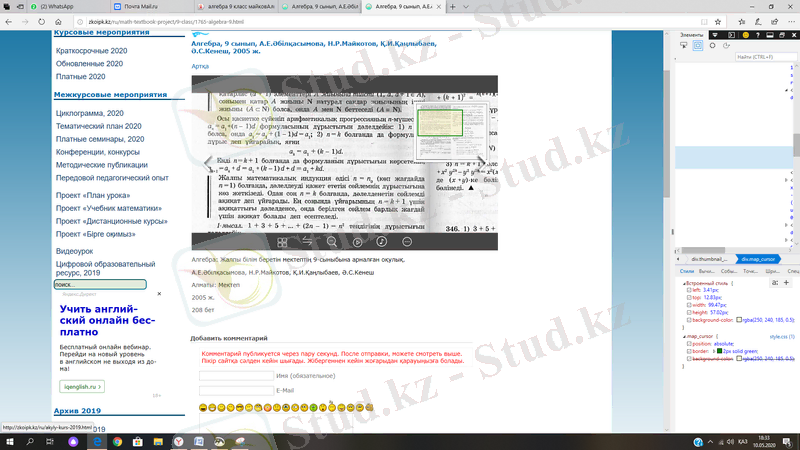
Десе де математикалық индукция тақырыбын сан тізбегі, прогрессиялардан соң беретіндігі дұрыс деп ойлаймын.

1. 2 Ресей орта мектептерде қолданыста болған және қолданыстағы оқулықтарындағы «Математикалық индукция» тақырыбына шолу және оларға анализ

Колягин Ю. М., Ткачева М. В, Федорова Н. Е. және басқалар, . Жижченко А. Б редакциялауымен «Алгебра и начала математического анализа (базовый и профильный уровни) » оқулығында математикалық индукция тақырыбы мысалдан басталған. Жаңадан басталған тақырып оқушыларға түсіндірілместен толық емес индукция, толық индукция әдісі бойынша дәлелдейік деген. Оны оқушылар бірден түсіне қоймайды. Одан кейін бары математикалық индукция әдісі төмендегідей берілген:

Анықтамаға назар аударсақ, алдымен айтылым-утверждение берілсін дейді, ал ол не?! Оның анықтамасы да түсіндірмесі де берілмейді.

1) және 2) қадамдар дәлелденгеннен кейін неге 2, 3, 4 сандары үшін орындалатындығын ашып айтпаған. Оны мектеп жасындағы оқушының өз бетімен түсінуі мүмкін емес.

Келесі оқулық Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова және С. А. Теляковскийдің Алгебра 9 сынып (учебник для общеобразовательных учереждений) оқулығы.

$C:\Users\Student\AppData\Local\Packages\Microsoft.MicrosoftEdge_8wekyb3d8bbwe\TempState\Downloads\IMG_20200506_161728 (1).jpg$

: $C:\Users\Student\AppData\Local\Packages\Microsoft.MicrosoftEdge_8wekyb3d8bbwe\TempState\Downloads\IMG_20200506_161827 (2).jpg$

Аталмыш оқулықта тақырыптың методологиясы көп оқулықтарға қарағанда дұрыс берілген. Ең бастысы көп оқулықтарда математикалық индукция әдісінің мүлдем мән берілмейтін жағы қарастырылған: ол - дәлелденіп отырылған тұжырымның неге екі қадамды дәлелдеу арқылы кез келген натурал сан үшін дұрыс деген қорытынды шығара алатындығын мысал арқылы көрсеткен. Бір ғана кемшілігі оқулықтағы математикалық индукция тақырыбына берілген тапсырмалар саны аз және 2 мысалда көрсетілген сандардың бөлінгіштік қасиетін дәлелдеуге мүлде тапсырма жоқ. Математикалық индукция тақырыбы дәл осы бөлінгіштік тақырыбындағы дәлелдеулерге таптырмас құрал немесе аппарат деуге болады. Яғни 2 мысал бойынша бекіту тапсырмалары жоқ.

И. Я. Виленкин, Г. С. Сурвилло, А. С. Симонов, А. И. Кудрявцев. Алгебра 9-класс Математикалық Индукция анықтамасы келесі түрде берілген. Бұл оқулықта математикалық индукцияның анықтамасын берудің алдында түсінікті етін мысал берілген. Анықтаманы бергенде тұжырымды бірден айтып кететін жері күрлелілеу, яғни оқушының түсінуіне қиындық келтіреді. Тапсырмалары да күрделі болып келген. Алайда, тапсырма легі көп болғанымен деңгейлері дұрыс қойылмаған.

$C:\Users\Мухамедали\Desktop\виленкин.PNG$

Сондай - ақ 9 сынып кейінгі жылдарда шыққан жалпы білім беретін мектептерге арналған оқулықтарда математикалық индукция әдісі туралы мүлдем айтылмаған. Атап айтсақ, Г. В. Дорофеевтің 9 сыныпқа арналған алгебраларында, Муравин Г. К, Кузнецова Е. П, Шнеперман Л. Б. 9 сыныпқа арналған оқулығы, Алимов Ш. т. б. 9 сыныпқа арналған жалпы білім беретін мектепке арналған оқулықта және т. б. бұл әдіске тоқталмаған.

1. 3 Шетел мектептерінде қолданыста болған және қолданыстағы оқулықтарындағы «Математикалық индукция» тақырыбына шолу және оларға анализ

Диссертацияны жазу барысында, яғни өз зерттеулерімді бастағанда бірден әдебиеттермен жұмыс жасауыма тура келді. Осы орайда Отандық, Ресей, ТМД елдерінің математикалық индукция тақырыбын беруі мен бірге шетелдік оқулықтар туралы жазылған мақалалармен де таныстым. Көптеген Әлемдік деңгейдегі педагог-математиктердің жұмысын [11-14] қарасырып, зерттеп, зерделедім. Солардың біразына тоқталып өткім келіп отыр.

Австралиялық ғалым Мэтью т. Майклсон [11] Квинсленд технологиялық университеті профессорының математикалық индукцияны берудегі педагогикалық зерттеу шолу жасаған мақаласында бұл әдісті берудің ерекшеліктері мен құндылығына тоқталған. Және оның қай жастан бастап беру керектігінің тиімділігін мақаланың негізгі арқауы ретінде қарастырған.

«Математикалық индукция-бұл математикалық тұжырымдардың шынайылығын анықтау үшін қолданылуы мүмкін дәлелдемелер әдісі. Бұл кәсіби практикалық құжат математикалық индукция түсінігін ұсынады, ол австралиялық оқу бағдарламасына қалай қатысты: математика және орта мектеп мұғалімдері бұл техникаға студенттер үшін жақындай алады. Атап айтқанда, дәлелдеме бойынша әдебиет ұсынылады - атап айтқанда, математикалық индукция және бірнеше пысықталған мысалдар шешуге байланысты негізгі қадамдарды бейнелейтін болады. Сабақ беру және оқыту саласындағы әртүрлі ескертулерді зерделегеннен кейін мақала орта сыныпта пайдаланылуы мүмкін математикалық индукция міндеттерінің кейбір мысалдарымен аяқталады.

Математикалық индукциямен техникалық мәселелер дәлелдемелерді әзірлеу үшін қажетті қадамдар арқылы жұмыс істей алмайтын студенттерді қамтиды. Жоғары сынып оқушыларына да, жоғары оқу орындарының студенттеріне да арналған зерттеуде Бейкер (1996) " формальды математикалық фон жеткіліксіз "(16-бет) және" математикалық мазмұнды жеткіліксіз білу " (15-бет) студенттердің математикалық индукция көмегімен дәлелдеме жасауға қабілетсіздігіне ықпал ететін іргелі факторлар болып табылады. Авиталь және Либескинд (1978) сияқты негізгі алгебралық аргументтерді жүзеге асыра алмайтынын, сондай-ақ студенттер математикалық білім берудің дәлелдемелерін индукциялау кезеңінде алгебралық манипуляцияларда кездесетін мәселелерге кеңінен түсініктеме берді. Сол сияқты Эрнест (1984) индукция кезеңінде k + 1 n-ге ауыстыру көптеген студенттер үшін проблема болып табылатынын атап өтті. »- дейді Мэтью Австралия математикалық журналындағы мақаласында. Жалпы жұмыста мектептен көпжылдар бойы алынып тасталынған, ал кейбір мектептерде 11 сыныпта берілгендіктен жоғары сынып оқушылары математикалық индукция ідісін толық меңгеруге іргелі математикалық білімдері жеткіліксіз екендігін айтып өткен.

Гил Рон және Томми Дрейфус [ 12] (Тель-Авив университеті, Израиль) Математикалық индукция әдісімен дәлелдеу оқыту модельдерін қолдану атты мақаласында да оқытушылармен сұхбаттасып, осы тақырыпты оқушыларға қай сыныптан беру керектігін зерттеген.

«Математикалық индукция көмегімен дәлел жоғары сынып оқушылары үшін тұжырымдамалық қиын екені белгілі. Бұл мақалада математикалық индукцияны оқытуда модельдерді қолдануға қатысты орта мектептің алты тәжірибелі оқытушыларымен сұхбат нәтижелері берілген. Модельдерді шығармашылық және барабар пайдаланумен қатар біз олардың негізінде жатқан математикалық идеяларды бұрмалайтын және мұғалімдердің концептуалды қиындықтарын көрсететін түсініктер, модельдер мен мысалдар таптық. Израиль орта мектебінің оқу бағдарламасы жоғары және орта деңгейдегі сыныптар үшін математикалық индукция арқылы дәлелдемелерді қамтиды. Әдетте 11-сыныпта математикалық индукция көмегімен теңдеу, теңсіздік және бөлінудің қасиеттері сияқты алгебралық қатынастарды дәлелдеуге үйретеді. Математикалық индукция арқылы дәлелдеме-бұл әрбір натурал сан үшін шынайы тұжырымдарды дәлелдеу әдісі. Математикалық индукцияның көмегімен дәлелдеу үшін N әрбір натурал сан үшін шынайы, екі шарттың әділдігін орнату қажет: N=1 үшін шынайы; егер бекіту k кез келген натурал сан үшін шынайы болса, онда ол сондай-ақ оның мұрагері k+1 үшін шынайы. Осы жұмыста бірінші шарттағы валидация кейде индукциялық базис деп аталады, ал екінші шарттағы валидация кейде индукциялық қадам деп аталады. Сонымен қатар, екінші жағдайда қолданылатын болжам, атап айтқанда, K үшін шынайы мәлімдеме индукция гипотезасы деп аталады, яғни математикалық индукция арқылы дәлелдемелерді оқыту үшін модельдерді пайдалану туралы білу болып табылады. Мұғалімдер қандай модельдерді пайдаланады? Олар осы модельдердің көмегімен нені және қалай түсінуге ниетті? Атап айтқанда, біз мұғалімдердің модельдерді қолдануы олардың елестетуді, көрсетуді немесе бейнелеуді қалайтын математикалық идеяларға сәйкес келетін мағынада барабар екенін білгіміз келеді. Бұл мақалада біз индукциялық Базис үшін модельдерді пайдалануға қатысты, атап айтқанда N=1 үшін тексеру және индукциялық қадам үшін модельдерді пайдалануға, атап айтқанда индукциялық гипотезаны дәлелдеуде пайдалануға қатысты қорытындылар ұсынамыз. Орта мектептің алты тәжірибелі математика пәні мұғалімі 30-60 минут бойы сұралды. Мұғалімдер, егер олардың ең болмағанда 10 жылдық педагогикалық өтілі болса, тәжірибелі деп саналды. Екі оқытушы математикалық білім беру саласында магистр дәрежесіне ие, ал үшеуі қазіргі уақытта осы дәрежені оқиды. Бір мұғалім (T6) - экономика және статистика факультетінің математика мұғалімі болу үшін ұзақ оқу курсынан өткен түлегі. Бұл мұғалім сондай-ақ математика мұғалімдерінің біліктілігін арттырудың үш жылдық бағдарламасына қатысты. Барлық мұғалімдер дәлелдемелерді математикалық индукция көмегімен кем дегенде екі рет сабақ берді, олардың кем дегенде екі жылда бір рет тікелей әңгімелесу алдында. Сұхбат жартылай құрылымды болды. Мұғалімдер біздің негізгі қызығушылығымыз модельді пайдалану болып табылатыны туралы хабардар болған жоқ. » Бұл ғалымдар Израиль мектептерінің математикалық индукция тақырыбын беруде қалай түсіндіретінін зерттегенін айтады. Сонда олар негізінен доминоны пайдаланып математикалық индукция әдісін үйрететіндігіне көз жеткізген. Және мұны ең тиімді жолдардың бірі ретінде қарастырады. Алайда сандардың бөлінгіштігі тақырыбын түсіндіргенде де математикалық индукция әдісін пайдаланатындығына тоқталған. Демек олар бұл әдісті жоғары сыныптар емес 5-6 сыныптарда да дейгейлеп берген дегенге тоқталуға негіз бар. Осы жұмыста біз математикалық индукцияны оқыту үшін модельдерді пайдаланудың кейбір аспектілерін қарастырамыз. Осылайша, біз модель ұғымын кең мағынада қолданамыз, физикалық модельдермен міндетті түрде шектелмейді. Модельдердің рөлі математикалық индукция көмегімен дәлелдеу әдісін көрсету, иллюстрациялау және түсіндіру, осылайша, математикалық индукцияны оқытуда қолданылатын формальды тілге қарағанда оқушылар үшін анағұрлым қолжетімді болуы мүмкін бейнелеу тілінің көмегімен түсінуді қолдау болып табылады- деген ойда Израиль ғалымдары.

Габриэль Дж. Стилианидис - Андреас Дж. Стилианидис-Джордж Н. Филиппу [13] Пенсильвания университеті, Оксфорд университеті, Кипр университеті ғалым-педагогтарының «Математикалық индукция арқылы дәлелдеме туралы мұғалімдердің білімін сақтау»-атты мақаласында осы турасын өте жақсы зерттеген.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.