Функцияны зерттеудің әдістері және экстремум есептерін шешудің әдістемелік негіздері


Тақырыптың өзектілігі
Математикада сан ұғымынан кейінгі негізгі ұғым функция ұғымы екендігі белгілі. Мектеп оқулықтарының барлық тақырыптары функция ұғымымен тығыз байланыста [1-5] .
Функция ұғымы ғылымға XVII ғасырда алдымен геометриялық және механикалық мағынада енді. Математикалық анализдің дамуымен байланысты XIX ғасырда оның алғашқы анықтамасы жалпы түрде берілді. Дәлірек айтқанда, неміс математигі Дирихле 1837 жылы енгізді. Қазіргі кезде орта мектепте «Функция және оның графигі», «Функцияны зерттеу» тарауын берудің әр түрлі тәжірибелері жинақталған. Оны оқыту әдістемесін оқулықтар мен журналдарда жарияланып жүрген мақалалардан көруге болады.
Мектеп математикасында функция тақырыбын оқыту мәселесі, әр заманда белгілі математиктер мен әдіскерлердің назарынан тыс қалмаған. Атап айтсақ А. Н. Колмогоров, Л. Д. Кудрявцев, Г. В. Дopoфeeв, М. К. Потапов, С. М. Никольский т. б. еңбектерінде функцияға қатысты мәселелер қарастырылған [6-8] .
Қазақстан ғалымдары мен әдіскерлері де осы мәселе төңірегінде ой қозғаған. Атап айтсақ, Н. Тeміpғaлиeв, М. Жайнибекова, Г. Воказе, Г. Aлeнoвa, М. Бeкжігітoвa еңбектері де осы тақырыпқа арналған [9-12] .
Қазіргі таңдағы еліміздегі білім беру жүйесінің ең басты міндеттерінің бірі білім берудің ұлттық моделіне өту арқылы жас ұрпақтың білім деңгейін халықаралық дәрежеге көтеру. Елдің алға қарай дамуының басты шарты -білімділік пен интелект, адамдардың рухани саулығы, дамудың жан-жақтылығы, оның кәсіби дайындығының кеңдігі мен икемділігі.
Дипломдық жұмыста ұсынылып отырған теориялық материалдар мен топтастырылған есептерді қарастыру, оқушылардың математикалық білім деңгейін көтеруде белгілі бір нәтижелерге жетуге септігі тиер деген ойдамыз.
Дипломдық жұмыстың мақсаты
Функцияны зерттеудің әртүрлі әдістеріне қатысты негізгі ұғымдарды анықтап, тақырыпқа қатысты есептерді іріктеу. Мектеп оқушыларының бойында функцияны зерттеудің әртүрлі әдістерінің жүйесін қалыптастыру - оларды ғылыми білім жүйесімен қаруландыру, әртүрлі пәндік бағыттардағы экстремалды есептерді шешу әдістерін жүйелеу және жалпылау.
Дипломдық жұмыстың құрылымы
Дипломдық жұмыс кіріспеден, екі тараудан және қорытынды мен пайдаланылған әдебиеттер тізімінен, қосымшадан тұрады.
Кіріспеде жұмыстың өзектілігі, мақсаты айқындалған.
І тарауда функция және дифференциалдық есептеудің негізгі ұғымдарының пайда болуы мен дамуы, орта мектептегі математика сабағында есеп шығарудың маңыздылығы қарастырылған.
ІІ тарауда функцияның ең үлкен және ең кіші мәндеріне байланысты берілген физикалық және экономикалық есептерді шешудің әдістемелік аспектілеріне тоқталы. Пайдаланылған дерек көздерінің тізімі көрсетілген.
Қосымшада «Функцияны зерттеудің әртүрлі әдістері» тақырыбы бойынша сабақ жоспары келтірілген.
1 Функция ұғымының қалыптасуы мен дамуы
- Функция ұғымының қалыптасу кезеңдері
Функция ұғымының қоршаған ортаны тануда үлкен рөл атқаратындығы белгілі. Шамалар арасындағы алғашқы математикалық қатынастардан, сандарға қолданылатын алғашқы ережелерден, фигуралардың ауданы мен көлемін табудың алғашқы формулаларынан бастау алған функционалдық тәуелділік осы идеяның ертеден басталғанын білдіреді [13-14] . Математикаға айнымалы ұғымының енуімен XVIIғ. функционалдық тәуелділікті қолдану және оны зерттеу басталды. Функция туралы алғашқы анықтаманы Декарт «Геометрия» атты еңбегінде ұсынды. Бұл еңбегінде ол алгебралық теңдеулер көмегімен ғана дәл бейнелейтін қисықтарды қарастырды. Біртіндеп функция ұғымы оның аналитикалық сипаттамасы-формуламен берілді. Функция сөзін (лат. function- «аяқтау, орындау») Г. В. Лейбниц берілген немесе басқа бір міндеттерді орындаушы шама мағынасында қолданды. x-тен функция терминін алғаш
Г. В. Лейбниц пен оның шәкірті И. Бернулли қолданды. Сондай-ақ 1698 жылдан бастап Г. В. Лейбниц айнымалы және константа (тұрақты) терминдерін енгізді. 1718 ж. Швейцариялық математик И. Бернулли функцияға дәл анықтама берді:
«Функция деп айнымалы шама мен тұрақтыдан қандайда да бір тәсілмен құрылған шаманы айтады». Л. Эйлер «Анализге кіріспе» (1748ж. ) атты кітабында функция анықтамасын былай тұжырымдайды: «Айнымалы шаманың функциясы дегеніміз - осы айнымалы шамамен сандардан немесе тұрақты шамадан құрылған аналитикалық өрнек». Л. Эйлер қазіргі кезде қабылданған функцияның белгілеулерін енгізген. Функцияның берілу тәсілі қолданылмайтын сандық функцияның қазіргі анықтамасын орыс математигі Н. И. Лобачевский (1834 ж. ) мен неміс математигі П. Дирихле (1837 ж. ) бір-біріне тәуелсіз берген. Бұл анықтамалардың негізгі мағынасы мынандай: «Егер x-тің әрбір мәніне y-тің белгілі бір мәні сәйкес келсе, онда y бұл сәйкестіктің формуламен, графикпен, кесте түрінде немесе сөзбен берілгеніне қарамастан, x айнымалысының
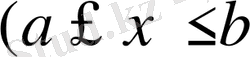 кесіндісінде) функциясы болады». Анықталу облысы мен мәндер жиыны таңдап алынатын қазіргі кездегі функция туралы түсінік
кесіндісінде) функциясы болады». Анықталу облысы мен мәндер жиыны таңдап алынатын қазіргі кездегі функция туралы түсінік
XX ғ. бірінші жартысында жиындар теориясын жасаған Г. Кантордың (1845-1918) еңбегінде тұжырымдалды.
Экстремалды есептер - максимум және минимумға арналған есептер біздің өмірімізде үлкен рольатқарады. Мұндай есептерді әр түрлі мамандықтардың өкілдерінің шешуіне тура келеді. Технологиялық инженерлер өндірісті мүмкіндігінше көп өнім өндіретін етіп ұйымдастыруға тырысады; дизайнерлер ғарыш кемесіне оның массасы ең аз болатындай етіп құрылысты жасауға тырысуда; экономистер зауыттың шикізат көздерімен байланысын көлік шығындары минималды болатындай етіп жоспарлауға тырысады. Әрбір ұйым біршама жұмыс жасау қажеттілігіне тап болады, ресурстарды мүмкіндігінше аз жұмсайды. Мұнда оңтайландыру мәселелерін шешудің әдістері көмекке келеді, олар менің жұмысымда талқыланады. Осы проблемалардың болуы және оларды шешудің әдістері біздің өмірімізде математиканың қажеттілігінің айқын мысалы болып табылады.
Ғылым мен техниканың дамуы математиканың әртүрлі бағыттарының дамуына байланысты. Қазіргі уақытта математика өндірісті ұйымдастыру мәселелерін шешудің, еңбек өнімділігін арттыруға көмектесетін оңтайлы шешімдерді табуға көмектесетін құралға айналуда.
Көптеген қолданбалы проблемалар экстремумдағы функцияларды зерттеуге дейін азаяды. Атап айтқанда, экономикалық теорияда математикалық бағдарламалау мәселесі көбінесе шартты экстремум проблемасына түседі. Функцияның экстремумын оның айнымалыларына шектеулер болған жағдайда іздеудің ең ыңғайлы тәсілдерінің бірі, яғни шартты оңтайландыру мәселесін шешу, Лагранж көбейткіштерінің әдісі болып табылады. Лагранж әдісінің негізгі практикалық құндылығы - бұл шартты оптимизациядан шартсызға көшуге мүмкіндік береді.
Алгебра курсы әртүрлі материалдарды қамтиды, алайда оның бөлімдерінің бірі экстремалды шамаларды табу мәселесі болып табылады. Сонымен, мұндай мәселені қалай шешу керектігін білу көптеген мәтіндік мәселелерді шешуде пайдалы, өйткені олардың шешілуін едәуір жеңілдетеді.
Шектен тыс мәселелерді шешу тек теориялық қызығушылық тудырмайды.
Кейде адамның практикасы мен күнделікті қызметіне байланысты тапсырмалар осындай мәселелерді шешуге дейін азаяды. Сондай-ақ, мұндай теңдеулер кейде физика мен геометрияда, эконимикада көптеп кездеседі.
Жоғарыда айтылғандардың барлығы дипломдық жұмыстың таңдалған тақырыбының өзектілігін көрсетеді.
Зерттеудің мақсаты - Зерттеу нысандары математикалық талдау әдістері болды.
Зерттеу пәні - шамалардың шамадан тыс шамаларын табу және оларды шешу әдістері.
Зерттеу мақсаты, объектісі және тақырыбы келесі тапсырмаларды таңдауды анықтады:
- функцияның экстремумы туралы ұғымды қарастыру, жергілікті және ғаламдық экстремумды, сонымен қатар функцияның экстремумының нүктелерін зерттеу;
- функцияның экстремумы үшін қажетті және жеткілікті жағдайларды зерттеу;
- функцияның экстремумының нүктелерін табу алгоритмін сипаттаңыз;
- алгебра және геометриядағы төтенше мәселелерді қарастыру;
- экстремалдың экономикалық және өндірістік проблемалардың ерекшеліктерін бөліп көрсету;
- басқа ғылымдардағы төтенше мәселелерді қарастыру.
1. 2 Дифференциалдық есептеудің негізгі ұғымдарының пайда болуы мен дамуы
Дифференциалдық есептеудің негізгі ұғымы-туынды физика, механика және математика есептерін, атап айтсақ, түзусызықты бір қалыпсыз қозғалыстың жылдамдығы мен кез келген қисыққа жанама жүргізуге байланысты есептерді шешу кезінде XVI ғасырда пайда болды. XV- XVII ғасырларда кез келген нүктеге жанама жүргізудің жалпы әдісін табу мәселесі көптеген математиктерді қатты ойландырды [1, 128-бет] .
Жалпы есептерді шешудің кейбір дербес жағдайлары ежелгі заманда берілген еді. Мысалы, Евклидтің «Бастамалар» еңбегінде шеңберге жанама жүргізу әдісі берілген. Архимед өз атымен аталатын ширатылымға (спиральға) жанама жүргізсе, ал Апполоний жанаманы эллипс, гипербола және параболаға жүргізген. Алайда ежелгі грек ғалымдары есепті аяғына дейін шешкен жоқ, яғни қандай да бір қисықтың кез келген нүктесіне жанама жүргізудің тиімді жалпы әдісін таппаған.
XVII ғ. басында кейбір ғалымдар, оның ішінде Торричелли, Вивиани, Роберваль, Барроу бұл сұрақтың шешімін кинематикалық тұрғыда іздей бастайды. Алгебралық қисыққа жанама жүргізудің бірінші жалпы әдісі Декарттың «Геометрия» атты еңбегінде көрсетілген. Ферманың жанамалар жүргізу әдісі дифференциалдық есептеулерді дамытудағы жалпы және маңызды әдіс болып табылады. Ферманың нәтижелері мен кейбір басқа да қорытындыларға негіздей отырып Лейбниц сәйкес алгоритм құрған және есепті алдыңғы ғалымдарға қарағанда толығырақ шешкен.
Қазіргі кезде қолданылып жүрген
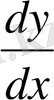 туынды символын Лейбниц
туынды символын Лейбниц
көрсеткен. Бірақ ол негізгі ұғымды туынды емес, дифференциал деп берген.
XVIII ғ. ортасында Эйлер айнымалы шаманың өсімшелерін белгілеу үшін гректің ∆ әрпін қолданған, әғни
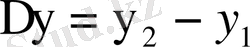 ,
,
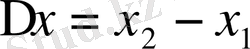 және т. с. с. Бұл белгілеу қазірге дейін сақталған.
және т. с. с. Бұл белгілеу қазірге дейін сақталған.
Туындының
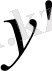 және
және
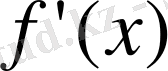 белгілеулерін Лагранж негізген.
белгілеулерін Лагранж негізген.
Туынды ұғымының ғылым мен техникада қандай үлкен рөл атқаратынын көрсететін мысалдарды көптеп келтіруге болады. Мысалы, үдеу - уақыт бойынша жылдамдықтың туындысы, дененің жылу сыйымдылығы - температура бойынша жылу көлемінің туындысы, радиактивті ыдырау жылдамдығы - уақыт бойынша радиоактивті зат массасының туындысы болып табылады және т. с. с. Туындыларды есептеу әдістері мен қасиеттерін игеру және оларды функцияларды зерттеуде қолдану дифференциалдық есептеудің негізін құрайды.
Maximum және minimum сөздерін латын тілінен аударғанда, сәйкесінше «ең үлкен» және «ең кіші» деген мағына береді. Геометриялық шамалардың ең үлкен және ең кіші мәндерін табудың кейбір дербес сұрақтарымен ежелгі грек математиктері де айналысқан.
Ежелгі грек математигі Евклид өзінің «Бастамалар» атты еңбегінде мағынасы мынадай ұғымды білдіретін сөйлемді дәлелдейді (таза геометриялық тұрғыда) : берілген үшбұрышқа іштей сызылған барлық параллелограмдардың арасынан табаны үшбұрыштың табанының жартысына тең параллелограмның ауданы ең үлкен болып табылады.
Жаңа ғасырдың басында жаратылыстану, ғылым мен техника есептері шамалардың ең үлкен және ең кіші мәндерін табу үшін жалпы әдісті қажет етеді. Сол кездің өзінде неміс математигі И. Кеплер (1615) шаманың максимум маңайындағы өзгерісі шамалы ғана дей отырып, экстремумды табу кезінде туындыны нөлге теңестіру туралы идея айтқан. Француз математигі П. Ферма өзінің «Максимумдар мен минимумдарды зерттеу әдісі» деп аталатын еңбегінде шек және туынды ұғымдарын қолданбаған, оның экстремумдарды анықтау әдісі біз қолданып жүрген және негізінде туындыны нөлге теңестіру болып табылатын Г. Лейбниц пен И. Ньютонның әдістеріне сәйкес келеді.
П. Ферма берілген шарға көлемі ең үлкен конусты, беті ең үлкен болатын цилиндрді іштей сызу есептерінен басқа есептерге де өз әдісін қолданған. Сонымен қатар өз әдісін тек бүтін алгебралық функцияларға ғана қолданып, ал экстремумдарды ажырату (максимумды минимумнан) критерийін қолданбағанын айта кеткен жөн. 1958 ж. голландиялық математик Б. Гудденің де берген максимумдар мен минимумдарды табу ережесі туралы осыны айтуға болады.
И. Ньютон (1671 ж. ) шамалардың ең үлкен және ең кіші мәндерін анықтауды, әғни кідіру принципін былай тұжырымдаған: «Егер шама барлық мүмкін болатын мәндердің ең үлкені немесе ең кішісі болса, онда осы мезетте ол өзгермейді». И. Ньютон өз ережесінің иррацианалдыққа да қолдануға болатындықтан Гудде ережесінің жалпы түрі болатынын екі мысалмен келтірген.
Максимумдар және минимумдар проблемаларын зерттеуге Лейбниц те маңызды үлес қосқан. Өзінің «Жаңа әдіс» (1684) атты еңбегінде ол функцияның өсу және кему аралығын зерттеуде біз қолданып жүрген дифференциал ұғымын пайдаланды, егер
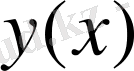 функциясының туындысы қандай да бір аралықта функция аргументінің өзгерісі кезінде оң болса, онда берілген функция осы аралықта өседі, ал туынды теріс болса, функция кемиді деген теореманы тұжырымдайды. Функцияның (экстремум болған жағдайда) ең үлкен немесе ең кіші ординатасы жанаманың көлбеу болмайтын шартымен, әғни дифференциал
функциясының туындысы қандай да бір аралықта функция аргументінің өзгерісі кезінде оң болса, онда берілген функция осы аралықта өседі, ал туынды теріс болса, функция кемиді деген теореманы тұжырымдайды. Функцияның (экстремум болған жағдайда) ең үлкен немесе ең кіші ординатасы жанаманың көлбеу болмайтын шартымен, әғни дифференциал
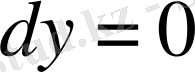 шартымен анықталады. Бұл жағдайда ординаталар «өспейді де, кемімейді де, бір қалыпта тұрады».
шартымен анықталады. Бұл жағдайда ординаталар «өспейді де, кемімейді де, бір қалыпта тұрады».
Эйлер (1755) өзінің «Дифференциалдық есептеу» атты еңбегінде функцияның мәні, мысалы, максимум нүктесінде осы функцияның ең үлкен мәнімен мүлдем сәйкес келмейтінін ескере отырып, абсолют экстремумдарды «негізгі сипаттамасы» деп аталатын салыстырмалы экстремумдардан ажыратты. Сондай-ақ ол көп айнымалы
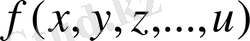 функциясының максимум және минимумдарын қарастырады. Функцияларды максимум мен минимумға зерттеу үшін Эйлер бірінші және екінші туындылармен ғана шектелмей, жоғары ретті туындыларды да қолданды.
функциясының максимум және минимумдарын қарастырады. Функцияларды максимум мен минимумға зерттеу үшін Эйлер бірінші және екінші туындылармен ғана шектелмей, жоғары ретті туындыларды да қолданды.
Максимумдар мен минимумдар туралы ілім біздің заманымызда уақытты тиімді пайдалану, өндірісті қажетті шикізатпен қамтамасыз етіп, еңбек өнімділігін арттыру жалпы экономиканы дамыту мәселелерінде маңызды ілімдердің бірі болып табылады.
1. 3 Функцияны зерттеудің әдістері
1. 3. 1 Функцияны туындының көмегімен зерттеу
Функцияның туындысы және үзіліссіздігі ұғымдары
Анықтама.
 функциясы
функциясы
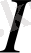 аралығында анықталсын. Егер
аралығында анықталсын. Егер
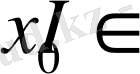 үшін
үшін
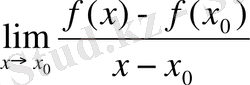
нақты мәнді шегі бар болса, онда
 функциясын
функциясын
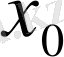 нүктесінде дифференциалданады, ал шектің мәнін
нүктесінде дифференциалданады, ал шектің мәнін
 функциясының
функциясының
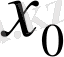 нүктесіндегі туындысы дейді де,
нүктесіндегі туындысы дейді де,
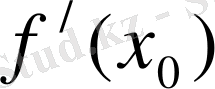 белгісімен белгілейді.
белгісімен белгілейді.
Осы амалды функцияны дифференциалдау, ал оның нәтижесін, яғни шектің мәнін функцияның туындысы дейді [17] .
Туындының анықтамасын шекті белгілейтін белгілерді қолданып, келесідей жазуға болады:
1°.
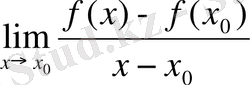 , 2°.
, 2°.
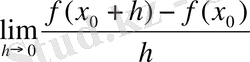 ,
,
3°.
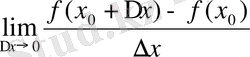 , 4°.
, 4°.
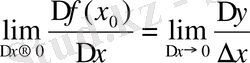 .
.
Соңғы екі жазуда
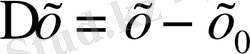 ,
,
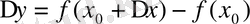 немесе
немесе
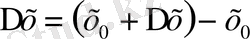 ,
,
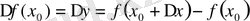 белгілеулері қолданылған.
белгілеулері қолданылған.
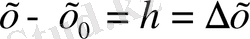 -ті функция аргументінің немесе тәуелсіз айнымалының өсімшесі, ал
-ті функция аргументінің немесе тәуелсіз айнымалының өсімшесі, ал
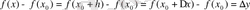 -ті функцияның өсімшесі деп атайды.
-ті функцияның өсімшесі деп атайды.
Туынды ұғымы - локальді ұғым.
Функцияның жиында дифференциалдануы, нүктеде дифференциалдануы арқылы анықталады:
 функциясы
функциясы
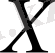 жиынында анықталсын. Егер
жиынында анықталсын. Егер
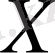 жиынының әрбір нүктесінде
жиынының әрбір нүктесінде
 функциясының ақырлы туындысы бар болса, онда
функциясының ақырлы туындысы бар болса, онда
 функциясының
функциясының
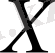 жиынында туындысы бар немесе
жиынында туындысы бар немесе
 функциясы
функциясы
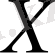 жиынында дифференциалданады дейді де,
жиынында дифференциалданады дейді де,
 символымен белгілейді.
символымен белгілейді.
“
 функциясы
функциясы
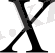 жиынында дифференциалданбайды” деген “
жиынында дифференциалданбайды” деген “
 функциясының кемінде бір
функциясының кемінде бір
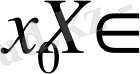 нүктесінде ақырлы туындысы жоқ” дегенмен пара-пар.
нүктесінде ақырлы туындысы жоқ” дегенмен пара-пар.
1-теорема
. Егер

 функциясының
функциясының
 нүктесінде туындысы бар болса, онда
нүктесінде туындысы бар болса, онда
 сол нүктеде үзіліссіз болады.
сол нүктеде үзіліссіз болады.
1-теоремаға кері теорема дұрыс емес: егер
 функциясы
функциясы
 нүктесінде үзіліссіз болса оның сол нүктеде туындысы әрқашанда бола бермейді. Демек, функция
нүктесінде үзіліссіз болса оның сол нүктеде туындысы әрқашанда бола бермейді. Демек, функция
 нүктесінде үзіліссіз бола тұрып, ол нүктеде дифференциалдануы да, дифференциалданбауы да мүмкін.
нүктесінде үзіліссіз бола тұрып, ол нүктеде дифференциалдануы да, дифференциалданбауы да мүмкін.
Салдар. Егер
 нүктесі
нүктесі
 функциясының үзіліс нүктесі болса, онда сол нүктеде
функциясының үзіліс нүктесі болса, онда сол нүктеде
 - тің ақырлы туындысы болмайды [17, 197-бет] .
- тің ақырлы туындысы болмайды [17, 197-бет] .
Функцияның үзіліссіздігі
Анықтама.
Егер кез келген
 саны бойынша
саны бойынша
 саны табылып,
саны табылып,
 , теңсіздіктерін қанағаттандыратын барлық
, теңсіздіктерін қанағаттандыратын барлық
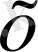 үшін
үшін
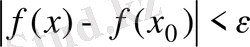 теңсіздігі орындалатын болса, онда
теңсіздігі орындалатын болса, онда
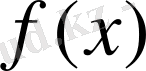 функциясын
функциясын
 нүктесінде үзіліссіз деп атайды. Яғни,
нүктесінде үзіліссіз деп атайды. Яғни,
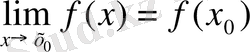 (3)
(3)
Жоғарыда берілген анықтамадан,
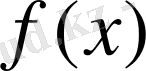 функциясының
функциясының
 нүктеде үзіліссіздігі келесі үш шарттың орындалуын білдіреді:
нүктеде үзіліссіздігі келесі үш шарттың орындалуын білдіреді:
1)
 функциясы
функциясы
 нүктесінде және оның қандай да бір
нүктесінде және оның қандай да бір
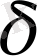 маңайында анықталған;
маңайында анықталған;
2)
 функциясының
функциясының
 нүктесінде шегі бар;
нүктесінде шегі бар;
3)
 функциясының
функциясының
 нүктесіндегі шегі функцияның сол нүктедегі мәніне тең.
нүктесіндегі шегі функцияның сол нүктедегі мәніне тең.
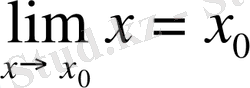 болғандықтан, үзіліссіздіктің анықтамасындағы (3) -теңдікті былай да
болғандықтан, үзіліссіздіктің анықтамасындағы (3) -теңдікті былай да
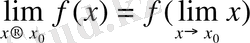 жазуға болады.
жазуға болады.
Демек, үзіліссіздікті шек таңбасы «lim» пен функция белгісі
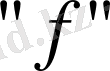 - ті өзара орын ауыстыру мүмкіндігі деп те анықтауға болады.
- ті өзара орын ауыстыру мүмкіндігі деп те анықтауға болады.
(3) - теңдікті
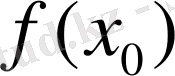 - ді теңдіктің сол жағына шек таңбасының астына көшіріп,
- ді теңдіктің сол жағына шек таңбасының астына көшіріп,
 болса
болса
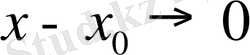 екендігін ескеріп,
екендігін ескеріп,
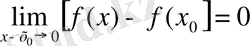 (4)
(4)
түрінде жаза аламыз. Мұндағы,
 айырымын аргументтің өсімшесі, ал
айырымын аргументтің өсімшесі, ал
 айырымын функцияның өсімшесі деп атайды.
айырымын функцияның өсімшесі деп атайды.
Егер
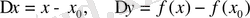 арқылы белгілесек, онда
арқылы белгілесек, онда
 болса
болса
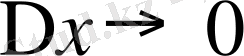 болатындықтан (4) - ті келесідей жаза аламыз:
болатындықтан (4) - ті келесідей жаза аламыз:
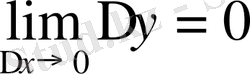 (5)
(5)
«Өсімше» терминін қолданып, үзіліссіздіктің анықтамасын былай айтуға болады: егер тәуелсіз айнымалының
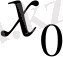 нүктедегі өсімшесі
нүктедегі өсімшесі
 нөлге ұмтылғанда, оған сәйкес
нөлге ұмтылғанда, оған сәйкес
 функциясының өсімшесі
функциясының өсімшесі
 нөлге ұмтылса, онда
нөлге ұмтылса, онда
 функциясын
функциясын
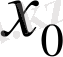 нүктесінде үзіліссіз деп атайды.
нүктесінде үзіліссіз деп атайды.
Мысалы,
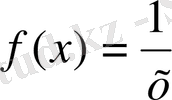 функциясы әрбір
функциясы әрбір
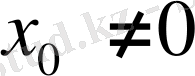 нүктесінде үзіліссіз.
нүктесінде үзіліссіз.
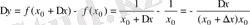
болғандықтан,
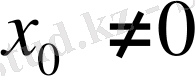 үшін
үшін
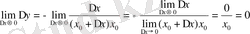 .
.
Сонымен, (5) -бойынша,
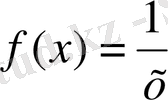 функциясы
функциясы
 нүктесінде үзілліссіз.
нүктесінде үзілліссіз.
Егер
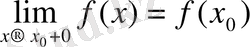 болса, онда
болса, онда
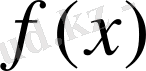 функциясын
функциясын
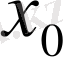 нүктесінде оң жақты үзіліссіз деп атайды;
нүктесінде оң жақты үзіліссіз деп атайды;
Егер
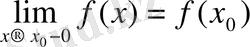 болса, онда
болса, онда
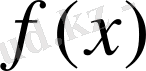 функциясын
функциясын
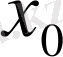 нүктесінде сол жақты үзіліссіз деп атайды.
нүктесінде сол жақты үзіліссіз деп атайды.
Егер
 функциясының анықталу аралығы
функциясының анықталу аралығы
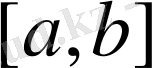 сегменті болса, онда
сегменті болса, онда
 функциясының
функциясының
 нүктесінде тек қана оң жақты, ал
нүктесінде тек қана оң жақты, ал
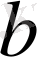 нүктесінде тек қана сол жақты үзіліссіздігі туралы айтуға болады.
нүктесінде тек қана сол жақты үзіліссіздігі туралы айтуға болады.
Үзіліссіз функциялардың кейбір қасиеттері
3-теорема . Егер
функциясы
нүктесінде үзіліссіз болса, онда
 нүктесінің қандай да бір
нүктесінің қандай да бір
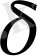 маңайында:
маңайында:
1)
 функциясы шенелген;
функциясы шенелген;
2) егер
 және
және
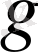 функциялары
функциялары
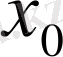 нүктесінде үзіліссіз болса, онда
нүктесінде үзіліссіз болса, онда
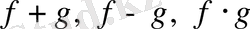 және
және
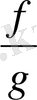
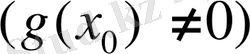 функциялары да сол нүктелерде үзіліссіз;
функциялары да сол нүктелерде үзіліссіз;
3) егер
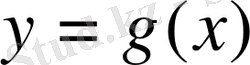 функциясы
функциясы
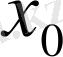 нүктесінде, ал
нүктесінде, ал
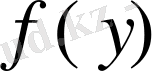 функциясы
функциясы
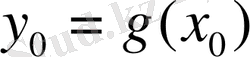 нүктесінде үзіліссіз болса, онда күрделі
нүктесінде үзіліссіз болса, онда күрделі
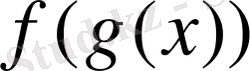 функциясы
функциясы
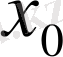 нүктесінде үзіліссіз болады.
нүктесінде үзіліссіз болады.
4-теорема
.
 функциясы
функциясы
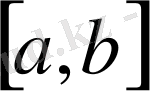 кесіндісінде қатаң монотонды және үзіліссіз болса, онда оған кері
кесіндісінде қатаң монотонды және үзіліссіз болса, онда оған кері
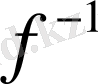 функциясы
функциясы
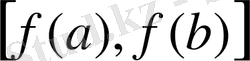 кесіндісінде қатаң монотонды және үзіліссіз болады.
кесіндісінде қатаң монотонды және үзіліссіз болады.
Анықтама.
Егер
 функциясы
функциясы
 нүктесінде анықталмаса немесе
нүктесінде анықталмаса немесе
 нүктесі анықталу жиынында жатып,
нүктесі анықталу жиынында жатып,
 сол нүктеде үзіліссіз болмаса, онда
сол нүктеде үзіліссіз болмаса, онда
 нүктесін
нүктесін
 -тің үзіліс нүктесі деп атап,
-тің үзіліс нүктесі деп атап,
 -ті
-ті
 нүктесінде үзіледі дейді.
нүктесінде үзіледі дейді.
Анықтама.
Егер
 нүктесі
нүктесі
 функциясының үзіліс нүктесі болып, сол нүктеде біржақты ақырлы шектері
функциясының үзіліс нүктесі болып, сол нүктеде біржақты ақырлы шектері
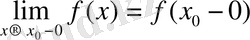 ,
,
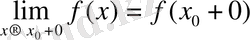
бар болса, онда
 функциясы
функциясы
 нүктесінде жай немесе бірінші түрдегі үзілісті дейді.
нүктесінде жай немесе бірінші түрдегі үзілісті дейді.
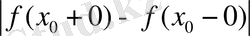 санын
санын
 функциясының
функциясының
 нүктесіндегі секірмесі деп атайды.
нүктесіндегі секірмесі деп атайды.
Егер
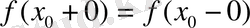 болса онда
болса онда
 - ді жөнделетін үзіліс нүктесі деп атайды.
- ді жөнделетін үзіліс нүктесі деп атайды.
Егер
 функциясы
функциясы
 нүктесінде үзілісті болып, бірақ үзілісі бірінші түрдегі үзіліс болмаса, дәлірек айтқанда,
нүктесінде үзілісті болып, бірақ үзілісі бірінші түрдегі үзіліс болмаса, дәлірек айтқанда,
 нүктесінде
нүктесінде
 - тің кемінде бір біржақты ақырлы шегі болмаса, онда
- тің кемінде бір біржақты ақырлы шегі болмаса, онда
 функциясын
функциясын
 нүктесінде күрделі немесе екінші түрдегі үзілісті дейді.
нүктесінде күрделі немесе екінші түрдегі үзілісті дейді.
Сонымен,
 функциясы
функциясы
 нүктесінде үзіліссіз болуы үшін
нүктесінде үзіліссіз болуы үшін
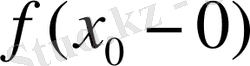 ,
,
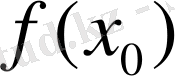 ,
,
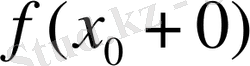 сандарының мағыналы болып, олардың өзара тең болуы қажетті және жеткілікті, яғни
сандарының мағыналы болып, олардың өзара тең болуы қажетті және жеткілікті, яғни
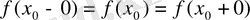 .
.
Мысалы,
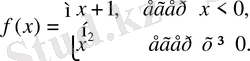 функциясын
функциясын
 нүктесінде үзіліссіздікке зерттейік.
нүктесінде үзіліссіздікке зерттейік.
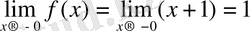 және
және
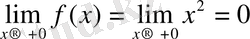
болғандықтан, функцияның
 нүктесіндегі біржақты шектері ақырлы, бірақ өзара тең емес. Демек,
нүктесіндегі біржақты шектері ақырлы, бірақ өзара тең емес. Демек,
 бірінші түрдегі үзіліс нүктесі.
бірінші түрдегі үзіліс нүктесі.
Негізгі элементар функциялар өздерінің анықталу жиынында үзіліссіз .
Анықтама.
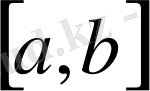 кесіндісінің әрбір нүктесінде үзіліссіз
кесіндісінің әрбір нүктесінде үзіліссіз
 функциясын кесіндіде үзіліссіз функция дейді.
функциясын кесіндіде үзіліссіз функция дейді.
Вейерштрасстың бірінші теоремасы.
Егер
 функциясы
функциясы
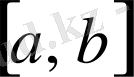 кесіндіде анықталған және үзіліссіз болса, онда оның мәндерінің жиыны шенелген жиын болады.
кесіндіде анықталған және үзіліссіз болса, онда оның мәндерінің жиыны шенелген жиын болады.
Вейерштрасстың екінші теоремасы
. Егер
 функциясы
функциясы
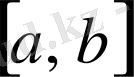 кесіндіде анықталған және үзіліссіз болса, онда осы кесіндіде ол ең үлкен және ең кіші мәндерін қабылдайды.
кесіндіде анықталған және үзіліссіз болса, онда осы кесіндіде ол ең үлкен және ең кіші мәндерін қабылдайды.
Больцано-Коши теоремасы
. Егер
 функциясы
функциясы
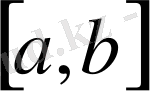 сегментінде үзіліссіз болып, сегменттің ұштарындағы мәндері
сегментінде үзіліссіз болып, сегменттің ұштарындағы мәндері
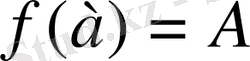 ,
,
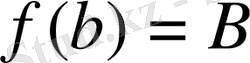 болса, онда
болса, онда
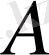 мен
мен
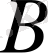 - ның арасында жатқан кез келген
- ның арасында жатқан кез келген
 үшін
үшін
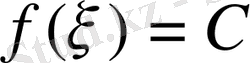 теңдігін қанағаттандыратын кемінде бір
теңдігін қанағаттандыратын кемінде бір
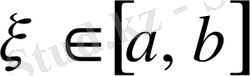 нүктесі табылады.
нүктесі табылады.
Ескертулер.
1. Вейерштрасстың бірінші теоремасы екінші теоремасының салдары болады, өйткені ең үлкен және ең кіші элементтері бар болатын нақты сандар жиыны сол екі санмен сәйкес жоғарыдан және төменнен шенелген.
2. Сегменттен өзге болатын әрбір аралықта үзіліссіз функция шенелмеген де, шенелсе де ең үлкен және ең кіші мәндері болмауы да мүмкін.
Мысалы, 1)
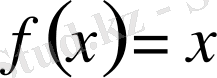 функциясы
функциясы
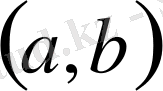 ақырлы интегрвалында үзіліссіз, шенелген бірақ ең үлкен де, ең кіші де мәндері жоқ, яғни бірде-бір
ақырлы интегрвалында үзіліссіз, шенелген бірақ ең үлкен де, ең кіші де мәндері жоқ, яғни бірде-бір
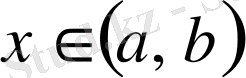 үшін
үшін
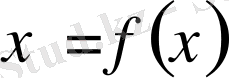 саны
саны
 -ға да,
-ға да,
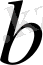 -ға да тең болмайды.
-ға да тең болмайды.
2)
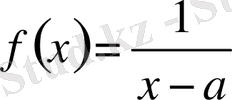 функциясы
функциясы
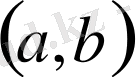 ақырлы интервалында үзіліссіз, жоғарыдан шенелмеген, төменнен шенелген.
ақырлы интервалында үзіліссіз, жоғарыдан шенелмеген, төменнен шенелген.
3)
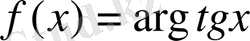 функциясы
функциясы
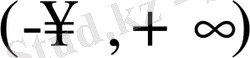 интервалында үзіліссіз, шенелген, бірақ ең үлкен де, ең кіші де мәндері жоқ [17, 190-бет] .
интервалында үзіліссіз, шенелген, бірақ ең үлкен де, ең кіші де мәндері жоқ [17, 190-бет] .
1. 3. 2 Функцияның экстремумдарын анықтау
5-теорема
.
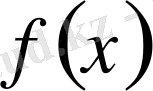 функциясы
функциясы
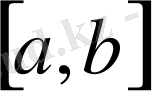 сегментінде үзіліссіз болып,
сегментінде үзіліссіз болып,
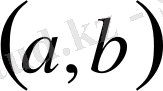 интервалында дифференциалдансын. Онда
интервалында дифференциалдансын. Онда
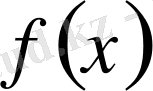 кемімейтін (өспейтін) болуы үшін әрбір
кемімейтін (өспейтін) болуы үшін әрбір
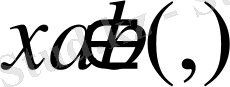 нүктесінде
нүктесінде
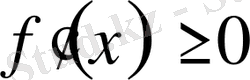
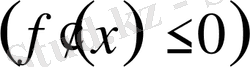 шартының орындалуы қажетті және жеткілікті.
шартының орындалуы қажетті және жеткілікті.
6-теорема
(экстремумның қажетті шарттары) .
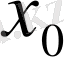 нүктесінің қандай да бір маңайында анықталған
нүктесінің қандай да бір маңайында анықталған
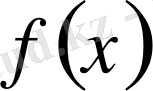 функциясының экстремум нүктесі
функциясының экстремум нүктесі
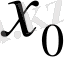 болсын. Онда,
болсын. Онда,
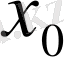 нүктесінде
нүктесінде
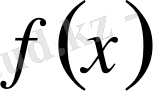 функциясының ақырлы туындысы жоқ немесе
функциясының ақырлы туындысы жоқ немесе
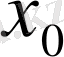 нүктесінде ақырлы туынды бар және нөлге тең, яғни
нүктесінде ақырлы туынды бар және нөлге тең, яғни
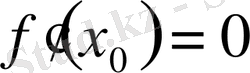 .
.
Локальді экстремумның қажетті шарты болатын бұл жағдайлардың әрқайсысы да жеткілікті шарт емес.
7-теорема
(экстремумның жеткілікті шарттары) .
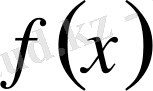 функциясы
функциясы
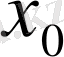 нүктесінің
нүктесінің
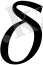 - маңайында үзіліссіз болып, оның ойылған
- маңайында үзіліссіз болып, оның ойылған
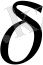 -маңайында дифференциалдансын (демек,
-маңайында дифференциалдансын (демек,
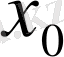 нүктесінің өзінде
нүктесінің өзінде
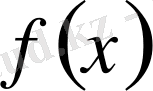 функциясының ақырлы туындысы болуы да, болмауы да мүмкін) .
функциясының ақырлы туындысы болуы да, болмауы да мүмкін) .
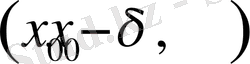 және
және
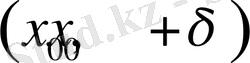 интервалдарының әрқайсысында
интервалдарының әрқайсысында
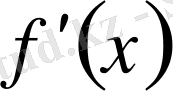 функциясы оң немесе теріс таңбалы болсын. Онда
функциясы оң немесе теріс таңбалы болсын. Онда
1) егер барлық
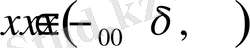 үшін
үшін
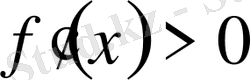 және барлық
және барлық
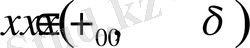 үшін
үшін
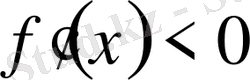 болса, онда
болса, онда
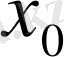 - локальді қатаң максимум нүктесі,
- локальді қатаң максимум нүктесі,
2) егер барлық
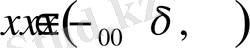 үшін
үшін
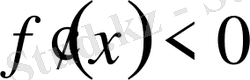 және барлық
және барлық
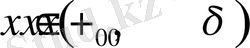
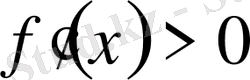 болса, онда
болса, онда
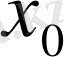 - локальді қатаң минимум нүктесі.
- локальді қатаң минимум нүктесі.
Мысалы,
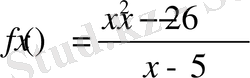 функциясының монотонды аралықтарын және экстремум нүктелерін анықтайық.
функциясының монотонды аралықтарын және экстремум нүктелерін анықтайық.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz