Жәй дифференциалдық теңдеулер жүйесі үшін екі нүктелі импульсті түрткілі шеттік есептің шешімін табудың алгоритмін құру

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 41 бет
Таңдаулыға:

Қазақстан Республикасы Білім және ғылым министрлігі

Параметрлеу әдісімен сызықты импульсті түрткілі шеттік есепті шешу

ДИПЛОМДЫҚ ЖҰМЫС

Мамандық: 5В060100 - Математика

Кіріспе

Көп салалардағы ауқымы кең есептерді оның ішінде, қозғалыстың траекториясын есептеуді немесе тербелімді жүйелерді зерттеуді, жәй дифференциалдық теңдеулер үшін импульсті түрткілі шеттік есептер терминдерінде тұжырымдауға болады.
Жәй дифференциалдық теңдеулер үшін импульсті түрткілі шеттік есептер теориясы көкейкесті және белсенді дамып келе жатқан дифференциалдық теңдеулердің сапалық теориясы мен қолданбалы математиканың бір саласы болып табылады. Қазіргі уақытта импульсті түрткілі шеттік есептердің мейлінше толық игерілген саласы екі нүктелі импульсті түрткілі шеттік есептер теориясы болып табылады. Импульсті түрткілі есептер сызықты емес механиканың зерттелуі Н.М.Крылов пен Н.Н. Боголюбовтың жұмыстарынан бастау алады. Заманауи техниканың дамуы импульстік системалардың зерттелу бағытын жаңа деңгейге көтергендей. Техника мен жаңа ақпараттық технологияның даму барысында жаңа леп әкелгендей. Десек те импульсті түрткілі есептерді зерттеуде киев мамематика мектебінің үлесі зор десек, артық айтпағанымыз. Атап айтсақ А.М.Самойленко, А.Д. Мышкис [3] , А.Халанай, Д.Векслер [4] және тағы басқалардың жұмыстарынан импульсті түрткілі сапалы дифференциалдық теңдеулерге байланысты теория қалыптаса бастады. А.М. Самойленко, Н.И. Ронто [5], А.М.Самойленко, Н.А.Перестюк [6], Н.А.Перестюк, В.Н. Шавкопляс [7], Ю.В.Роговченко, С.И.Трофимчук [9] және тағы басқалар.
Алғашқы жұмыстар жоғары ретті дифференциалдық теңдеулер және бірінші ретті дифференциалдық теңдеулер жүйесі үшін импульсті түрткілі шеттік сызықты есептердің шешілімділік шарттарын табуға арналды.
XIX ғасырдың соңында тербелімділік теориясының көптеген есептері периодтық коэффициентті дифференциалдық теңдеулерге келтірілді. Бұл арада осы теңдеулердің шешімдерінің орнықтылығын зерттеумен бірге олардың периодты шешімдерін табу қажеттігі пайда болды. Сызықтық шеттік есептерді зерттеудің негізгі құралы шешімдердің іргелі жүйесі және Грин функциясы болып табылды. Көптеген жұмыстар түрлі сызықтық шеттік есептер үшін Грин функциясын құруға және қасиеттерін зерттеуге арналды. Бұл кезеңдегі импульсті түрткілі шеттік есептерді зерттеудің негізгі нәтижелері Бунецкий мен Тамаркиннің монографиясында тұжырымдалды және бейнеленді. Жәй дифференциалдық теңдеулер үшін импульсті түрткілі шеттік есептерге келтірілетін қолданылымның көптеген есептері импульсті түрткілі шеттік есептер теориясын дамытудың қосымша түрткісі болды.
Жәй дифференциалдық теңдеулер үшін импульсті түрткілі шеттік есептер әртүрлі әдістермен К.К.Кенжебаев, Станжинский [ ], И.Рахунковой, Я Томечека [ ], Л.И.Каранджулова [ ], И.Бажо, Э.Лиз [ ], С.Г.Христова, Д.Д.Байнов [ ], И.Бажо, Н.Ян [ ], А.Б.Дишлиев, Д.Д.Байнов [ ], К.Шароп Каул [ ], В.Лакшимикантам, Д.Д.Байнов, П.С.Симеонова [ ], А.А. Мартынюк, Л.Н.Чернетская [ ] және тағы басқаларының жұмыстарында зерттелді.
Шеттік есептер теориясының дамуы, операторлық теңдеулерді зерттеу және шешімдерін табу әдістерінің дамуымен тығыз байланысты. Операторлық теңдеулерді зерттеудің топологиялық және итерациялық әдістері шеттік есептердің шешілімділік шарттарын алу мен олардың шешімін табу алгоритмдерін құруды қамтамасыз етті. Аналитикалық, функционалды-аналитикалық, сандық және сандық-аналитикалық әдістер жасалынды. Импульсті түрткілі шеттік есептерді зерттеу және шешудің негізгі әдістер тобы тұрғысында библиография және егжей-тегжейлі талдау А.М. Самойленко, Н.И.Ронто монографиясында келтірілген. Импульсті түрткілі шеттік есептерді зерттеу және шешудің мөлшерлі әдістері болуына қарамастан оларға деген қызығушылық осы күнге дейін бәсеңдеген емес. Соңғы жұмыстардың пайда болуы импульсті түрткілі шеттік есептердің қолданылу ауқымы кеңейтілуі белгілі әдістермен шешілмейтін есептердің тағысын тағы жаңа түрлері туындайтын және де осы теорияның шеттік есептер өзіндік дамуымен негізделеді. Әртүрлі ыңғай табу мен әдістер қолдану түрлі терминдерде тұжырымдалған нәтижелерге телінеді. Есептеу техникасын қолданбалы есептерді шешуде қолдану ұсынылған әдістерге жаңа талаптар қояды. Жасалынатын әдістерге қойылатын негізгі талаптардың бірі оның теоремалардың солардың негізінде алынатын шарттарын көрнекті түрде тексеруді мүмкін ететін және берілген дәлдік бойынша ізделінді шешімді табуды мүмкін ететін, конструктивтілігінде.
Қарапайым дифференциалдық теңдеулер үшін импульсті түрткілі шеттік есептер қолданбалы салаларда жиі пайда болады және ғылым мен техниканың әр алуан есептерін шешуде кең түрде пайдаланылады. Тиімді басқаруды табу есебін екі нүктелі шеттік есептерді шешуге алып келген Понтрягиннің максимум қағидасының жасалуы жәй дифференциалдық теңдеулер үшін шеттік есептер теориясына деген қызығушылықты едәуір арттырды.
Өткен ғасырдың 80-ші жылдары Д.С. Жұмабаевтің [27, 28] еңбектерінде қарапайым дифференциалдық теңдеулер үшін шеттік есептерді зерттеу мен шешуге арналған параметрлеу әдісі ұсынылған болатын. Параметрлеу әдісінің мәні - дифференциалдық теңдеу қарастырылатын аралық белгілі бір 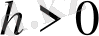қадаммен бөліктерге бөлінеді және бастапқы есеп параметрі бар пара-пар есепке келтіріледі. Параметрі бар есептің шешімі параметр мен белгісіз функцияның жұптарының жүйелерінің тізбегінің шегі ретінде анықталады. Параметр шеттік шарттар мен дифференциалдық теңдеулер жүйесі матрицалары арқылы құрастырылатын сызықты теңдеулер жүйесінен табылатын болса, ал белгісіз функциялар ұзындығы 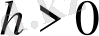болатын аралықтардағы параметрдің табылған мәндеріндегі Коши есебінің шешімі ретінде табылады. Параметрді енгізу параметрлеу әдісінің алгоритмдерінің жинақтылығы шарттарын қарастырып отырған есептің бастапқы берілгендер терминінде тағайындауға мүмкіндік берді, оған қоса бұл шарттар зерттелініп отырған есептің шешімінің бар болуы мен жалғыздығын қамтамасыз етеді. Параметрлеу әдісі қарапайым дифференциалдық теңдеулер жүйесі үшін шеттік есептің шешілімділігі шарттарын бастапқы берілімдер терминінде алуға және оның шешімін табу алгоритмдерін құруға мүмкіндік берді.
Қазіргі таңда, дифференциалдық теңдеулер жүйесі үшін шеттік есептер теориясы маңызды мәселелерінің біріне айналып отыр, оған себеп - табиғат пен қоршаған ортада болып жатқан көптеген құбылыстардың математикалық моделін құру кезінде аталған есептерді шешуді қажет етеді. Осыған байланысты, дипломдық жұмыста дифференциалдық теңдеулер жүйесі үшін екі нүктелі шеттік есебі параметрлеу әдісімен зерттеледі.
Кәсіпқойлық, педагогикалық, қолданбалы бағыттылыққа, математиканы саралап оқытуға, пәнаралық байланысты ашуға, өз бетімен танып білуді дамытуға оқу-әдістемелік әдебиеттермен қамтамасыз етуге арналған көптеген зерттеулер бар (Е.Ы. Бидайбеков [29, 30], А.Е. Абылқасымова [31, 32], Б.Б. Баймуханов [33], В.Н. Келбакиани [34], М.И. Махмутов [35], В.П Бепалько [36, 37], В.А. Гусев [38], В.А. Далингер [39, 40], И.Д. Зверев [41, 42], Е.У. Медеуов [43, 44], Н.В. Метельский [45], М.Н. Скаткин [46, 47], С.И. Шварцбург [48], А.А. Столяр [49], И.Т. Огородников [50], Х.А. Гербеков [51], Ю.М. Колягин [52], М.Р. Куваев [53], Л.Д. Кудрявцев [54], Г.Л. Луканкин [55], А.Г. Мордкович [56]). Барлық зерттеулер негізінде педагогикалық жоғарғы оқу орындарында математиканы оқыту әдістемесін жетілдіруге және дамытуға арналған.
Дифференциалдық теңдеулер әртүрлі физикалық, химиялық, биологиялық және басқа да жаратылыстанудың үдерістерін математикалық модельдеу кезінде жиі пайда болады. "Дифференциалдық теңдеу" терминінің өзі алғаш рет Г.Лейбництің И.Ньютонға жазған хаттарының (1676 жылы) бірінде кездеседі. Г.Лейбницті мұндай терминді қолдануына дифференциалдарды есептеуі әкелді деуге болады, бұл И.Ньютонның флюкциялар әдісі сияқты жоғары математиканың немесе шексіз аз шамаларды талдаудың бастамасы болып есептеледі. Дифференциалдық теңдеулердің шешімдерінің шексіз көп жиыны болатынын И.Ньютон атап көрсеткен болатын.
Шешім жалғыз болуы үшін қосымша шарттардың орындалуы жорамалданады. Жәй дифференциалдық теңдеулер үшін осындай шарттың бірі - Коши шарты, мұнда дифференциалдық теңдеумен қоса осы дифференциалдық теңдеу қарастырылатын аралықтың қандай да бір нүктесіндегі шешімнің мәні беріледі.
Алайда, көбінесе дифференциалдық теңдеудің шешімдер жиынтығынан ізделінді шешімді бөліп алатын қосымша шарттар қарастырылып отырған аралықтың бастапқы және соңғы нүктелеріндегі шешімнің мәндерінің арасындағы қатынастар түрінде беріледі. Мұндай шарттар шеттік шарттар деп аталады. Дифференциалдық теңдеудің шеттік шарттарды қанағаттандыратын шешімін табу қажет болғанда шеттік есеп берілген деп айтады.
Кең сыпаттағы мамандар дайындауда дифференциалдық теңдеулердің рөлі сонымен бірге оқыту мақсаты - мамандарды кәсіпқойлық-педагогикалық және ғылыми-іс-тәжірибелік дайындауда дифференциалдық теңдеулердің мүмкіндіктерін ашу және қолдануды да анықтайды [57, 58].
Тақырыптың өзектілігі. Студенттерге оқу бағдарламалары бойынша дифференциалдық теңдеулер мен математикалық физика теңдеулері пәндерін оқытуда әртүрлі есептердің шешу тәсілдерін қарастыру. Қолданбалы математиканың көптеген салаларында дифференциалдық теңдеулер үшін импульсті түрткілі шеттік есептер пайда болады. Тақырыптың өзектілігі бір жағынан ғылым мен техниканың әр түрлі мәселелерін шешуде жәй дифференциалдық теңдеулер үшін шеттік есептер теориясының практикалық қосымшаларының маңыздылығымен, ал екінші жағынан жәй дифференциалдық теңдеулер үшін импульсті түрткілі шеттік есептерді шешудің жаңа тиімді әдістерін құру қажеттілігімен байланысты анықталады.
Тақырыптың ғылыми жаңалығы. Сызықты екі нүктелі импульсті түрткілі шеттік есептің бірмәнді шешілімді болуының фундаменталдық матрица терминінде қажетті және жеткілікті шарттары алынды. Фундаменталдық матрицаны әр уақытта құруға мүмкіндік бермейтінін көрсететін мысалдар келтіріліп, параметрлеу әдісінің қажеттілігі көрсетілді.
Параметрлеу әдісі негізінде дифференциалдық теңдеулер үшін екі нүктелі импульсті түрткілі шеттік есептің шешімін табудың алгоритмі құрылып және оның жинақтылығының шарттары алынды.
MathCad программалау ортасында дифференциалдық теңдеулер үшін импульсті түрткілі шеттік есептердің жуық шешімдері табылып, олардың сызбалары келтірілді.
Зерттеудің мақсаты. Параметрлеу әдісі негізінде жәй дифференциалдық теңдеулер үшін сызықты екі нүктелі импульсті түрткілі шеттік есепті шешудің теориялық негіздерін қолданып, оқытудың тиімді әдіс-тәсілдерін жүзеге асыру.
Зерттеудің міндеті:
1. Жәй дифференциалдық теңдеулер жүйесі үшін сызықты екі нүктелі шеттік есептің бірмәнді шешілімді болуының фундаменталдық матрица терминінде қажетті және жеткілікті шарттарын алу.
2. Жәй дифференциалдық теңдеулер жүйесі үшін екі нүктелі импульсті түрткілі шеттік есептің шешілімділігінің шарттарын бастапқы берілгендер терминдерінде алу және оның шешімін табудың алгоритмін құру.
3. MathCad программалау ортасында жәй дифференциалдық теңдеулер жүйесі үшін импульсті түрткілі шеттік есептердің жуық шешімдерін табу.
Зерттеу нысаны. Жәй дифференциалдық теңдеулер жүйесі үшін сызықты екі нүктелі импульсті түрткілі шеттік есебі.
Зерттеу пәні. Дифференциалдық теңдеулер жүйесі үшін екі нүктелі шеттік есептің бірмәнді шешілімділігінің сұрақтары.
Зерттеу мақсатына жету үшін төмендегідей зерттеу есептері қойылды:
1. Сызықты екі нүктелі импульсті түрткілі шеттік есептің бірмәнді шешілімді болуының берілгендер терминінде қажетті және жеткілікті шарттарын алу.
2. Параметрлеу әдісін жәй дифференциалдық теңдеулер жүйесі үшін екі нүктелі шеттік есебіне қолдану.
3. Жәй дифференциалдық теңдеулер жүйесі үшін екі нүктелі импульсті түрткілі шеттік есептің шешімін табудың алгоритмін құру.
4. Құрылған алгоритм бойынша MathCad программалық пакетінде дифференциалдық теңдеулер жүйесі үшін импульсті түрткілі шеттік есептердің жуық шешімін табу.
Негізгі ғылыми нәтижелер:
1. Сызықты екі нүктелі шеттік есептің бірмәнді шешілімді болуының фундаменталдық матрица терминінде қажетті және жеткілікті шарттары алынды.
2. Параметрлеу әдісі жәй дифференциалдық теңдеулер жүйесі үшін екі нүктелі импульсті түрткілі шеттік есебіне қолданылды.
3. Жәй дифференциалдық теңдеулер жүйесі үшін екі нүктелі импульсті түрткілі шеттік есептің шешімін табудың алгоритмі құрылды.
4. Құрылған алгоритм бойынша MathCad программалық пакетінде дифференциалдық теңдеулер жүйесі үшін импульсті түрткілі шеттік есептердің жуық шешімі табылды.
Дәлдігі. Дипломдық жұмыста алынған ғылыми нәтижелер теоремалар түрінде тұжырымдалған және математикалық қатаң түрде дәлелденген. Тағайындалған тұжырымдар MathCad программалық пакетінде мысалдармен көрсетілген.
Зерттеу бағытын таңдау - дифференциалдық теңдеулер жүйесі үшін екі нүктелі импульсті түрткілі шеттік есептің бірмәнді шешілімділігін зерттеу және оның шешімін табу алгоритмін құру.
Бірінші тарауда дифференциалдық теңдеулер жүйесі үшін сызықты екі нүктелі шеттік есепті шешудің теориялық негіздері қарастырылады. Бірінші тараудың бірінші бөлімінде дифференциалдық теңдеулер үшін сызықты екі нүктелі шеттік есебінің қойылымы келтіріледі. Жәй дифференциалдық теңдеулер жүйесі үшін сызықты екі нүктелі шеттік есеп 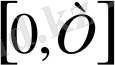кесіндісінде қарастырылады:

Екінші тарауда сызықты екі нүктелі шеттік есепті шешудің әдістемесі көрсетіледі. Екінші тараудың бірінші бөлімінде физика-математика бағытындағы мамандарды даярлаудағы дифференциалдық теңдеулердің рөлі мен орны көрсетіледі.
Жоғарғы оқу орындарында өткізілетін көптеген заманауи мамандықтардың негізгі пәндерінің бірі болып адамдардың ғылыми-практикалық және қоғамдық-өндірістік іс-әрекетінің барлық салаларын қамтитын математика пәні болып табылады. Математика әдістері түрлі құбылыстарды неғұрылым объективті түсінуге, оларды тиімді зерттеуге және алынған нәтижелердің анықтығын жоғарлатуға жағдай жасайды. Сонымен, математика дайындау математикалық әдістермен түрлі проблемаларды зерттеуде және шешуде, заманауи ақпараттық-есептеу техникасын қолдануда, іс жүзінде басқа техникалық жетістіктерді пайдалануға мүмкіндік беретін көптеген мамандықтар бойынша жоғары дәрежелі кадрларды даярлаудың бөлінбес бөлігі болады. Осылайша оқу мақсатын, көлемін және курстың мазмұнын берілген уақыттың шегін ескере отырып анықтау, оқытудың неғұрылым сәтті тәсілдерін таңдап алу басты кезең болуы ақиқат.
Дифференциалдық теңдеулерге келетін есептермен математиктер тіптен XVI ғасырдан бастап шұғылдана бастады.
Дифференциалдық теңдеулер курсы болашақ математиктерді, механиктерді және физиктерді, қалайша олардың математикалық мәдениетінің белгілі бір деңгейін қалыптастыру жағынан болса, солайша ғылыми көзқарасын қалыптастыру жағынан да іргелі математикалық дайындауда үлкен рөл атқарады. Дифференциалдық теңдеулермен бүкіл жаратылыстану идеологиясы, оның ішінде, жоғарыда айтып кеткендей, аспандық және квантты механика, тығыз байланысты, классикалық физика негізінде дифференциалдық теңдеулер тетігінде жүзеге асады. Мысалы П.Лаплас табиғаттың негізгі заңдары ғылыми-жаратылыстық болжамдар (детерминизм принципі) жасауды қамтамасыз ететін, дифференциалдық теңдеулер түрінде бейнеленеді деп есептеді. Осындай тұрғыдан Д.К.Максвелл электр-магниттік өрістің, П.Дирак - позитронның болуын алдын-ала болжады. Планеталар мен басқа аспан денелерінің қозғалыстарының дифференциалдық теңдеулерін зерттей отырып ғалымдар олардың қозғалу траекторияларын есептеді, кризистік жағдайларды алдын-ала айтып берді. Д.Адамс пен У.Леверье Уран планетасының траекториясын зерттей отырып, кейін астрономиялық бақылаулармен расталған, Галлей кометасын ашты.
Дифференциалдық теңдеулер физика-математика мамандықтары бойынша іргелі математикалық дайындауда орталық пән болып табылатын математикалық талдаудың логикалық жалғасы болып табылады. Математикалық талдау өзін қолданбалы есептерде дифференциалдық теңдеулер арқылы толыққанды жүзеге асырады. Шындығында да бұл шынайы, себебі функцияның туындысы қисыққа жанаманың бұрыштық коэффициенті, қозғалыстың лездік жылдамдығы, электрлік тізбекте токтің күші және т.т. ретінде, іс-тәжірибелік түсініктерді анықтайды. Екінші туынды қисықтың қисықтығын анықтау мүмкіндігін, үдеуді, токтің электрлік тізбектегі қозғалысын т.т. анықтайды. Дифференциалдық теңдеулер функцияны оның түрлі дәрежелі туындыларымен байланыстырады. Атап айта кету керек, И.Ньютон алғашқы функцияны табуды, функциямен оның туындысы арасындағы қатынас бойынша табу есебі, яғни негізінде дифференциалдық теңдеулерді шешу ретінде қарастырды.
Екінші тараудың екінші бөлімінде фундаменталдық матрицаны пайдаланбай-ақ, (0.1)-(0.4) есебінің бірмәнді шешілімділігінің қажетті және жеткілікті шартын алу мәселесі қарастырылады.

Параметрлеу әдісімен сызықты импульсті түрткілі шеттік есепті шешу

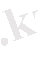
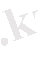
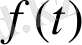вектор функциясы кесіндісінде үзіліссіз бөліктенген импульстің әсер ету нүктесінде , 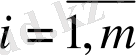бірінші текті үзіліс нүктесі болуы мүмкін вектор функция.

,

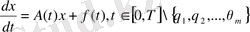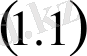
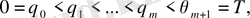
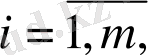
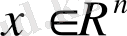
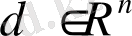
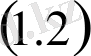
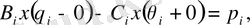
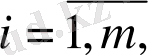
мұндағы: матрица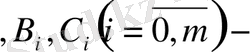тұрақты матрицалар.
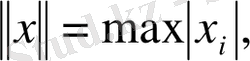
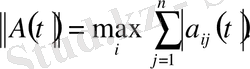
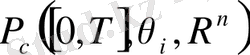арқылы үздіксіз бөліктенген белгілейік

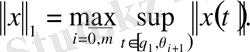
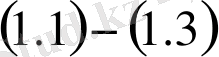есебінің шешімі 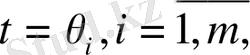нүктесінен басқа 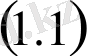дифференциалдық теңдеуді тепе-теңдікке айналдыратын 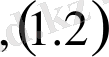шекаралық шартты 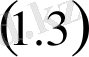импульсті түрткілі қазықталған уақыт моментінде 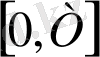кесіндісінде үзіліссіз бөліктенген 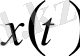вектор функциясын атаймыз.
Мысалдар қарастырайық, импульс белгіленген уақыт сәтіне әсерінің болуын екі нүктелі шеттік есебінде қарастырамыз.
1-мысалы: 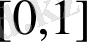аралығында периодты шеттік есебін қарастырайық:

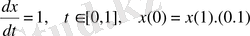
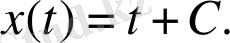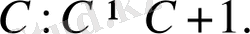Қарастырған теңдеудің жалпы шешімітүрінде болады.Қисықтың шартын қанағаттандырмайтында ішінде шешімдер бар. Нақты саны жоқ, теңдеудің шартын қанағаттандыратын, үшін кез -келгенСондықтан (0.1) периодты шеттік есебінің шешімі болмайды.
Енді, дәл осы теңдеуде және сол шеттік шарты мүмкін болатын, 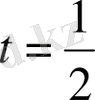болғанда шешімі импульстің әсерінен болады:

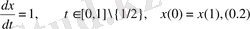
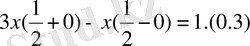
Қарастырған теңдеудің жалпы шешімі 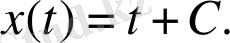түрінде болады.
Көрсетейк, импульстің әсерінің шарты 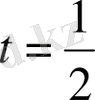болған нүктеде,-ны таңдауға мүмкіндік алады, 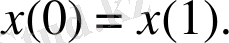периодтық шартын және (0.3) шартын орындайды. аралығы мына түрде болады. (0.3) шартына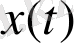нмәнін 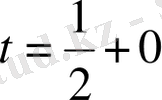нүктесінде табамыз:

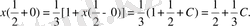
Периодты шеттік шартын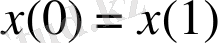, т.е. 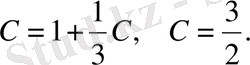қанағаттандыратындай шешімін тандандап аламыз. 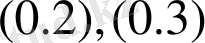есептерінің шешімі 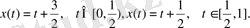функция болады.
Бұл функция шынындада есептің шартын қанағаттандырады:
1) 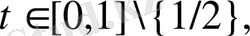болғанда 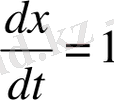дифференциалдық теңдеуді қанағатандырады.
2) Импульстің әсерінде 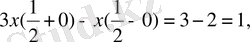қанағатандырады.
3) 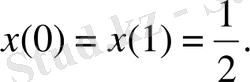периодтылық шарты.
Алдағы табылған функция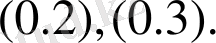есептің жалғыз шешімі болады.

2-мысалы:Импульстің әсерінсіз периодты шеттік есебін қарастырамыз:

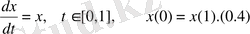
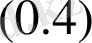есебінің жалғыз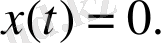шешімі болатыны айқын. 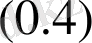периодты шеттік есебін импульстің әсерімен қарастырайық:

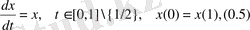
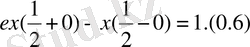
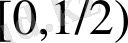теңдеудің жалпы шешімі мына түрде болады: 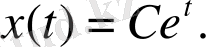Осыдан 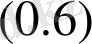айқындайық :

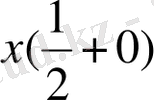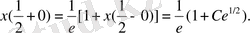
Онда 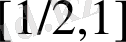шешімі мына түрде болады.
Енді,периодты шеттік шартын қанағаттандыратындай,еркін тұрақтыны С таңдап аламыз,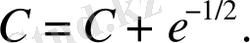теңдікті қанағаттандыратын болсын.
саны бар болмаса, онда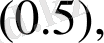есебінің шешімі болмайды.

Импульсті түрткілі есептердің бірмәнді шешілімділігі әртүрлі әдістермен зерттелген. Бұл жұмыста 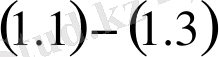есебі параметр әдісімен зерттеледі.
Параметрлеу әдісінің негізгі мағынасы дифференциалдық теңдеу қарастыратын қандайда бір 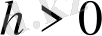қадаммен бөліктері бөліп бастапқы есепке эквивалентті параметрмен берілген есеп келтіріледі.
Шекаралық шарт пен дифференциалдық теңдеулер жүйесі анықталған матрица бойынша параметр табылады ал функция табылған параметр мәндерінде ұзындығы 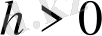интервалында Коши есебінің шешімі болады.
Осы табылған әдістің схемасын 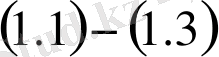есебін келтірейік.
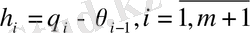болсын. санын алып

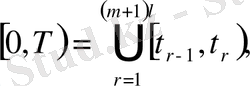
бөліктерге бөлеміз. Мұндағы импульс түрткілі нүктелер санына кіреді,
ал нүктелер арақашықтығы 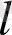бөлікке
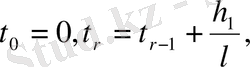
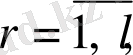
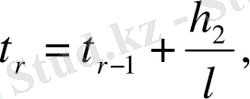
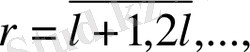
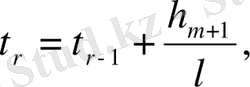
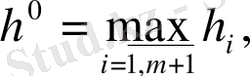
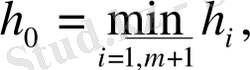
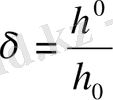
бөлінеді. 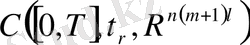кеңістікті және 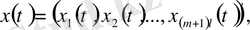функциялар жүйесін енгіземіз. Мұндағы 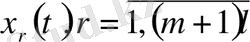функциясы 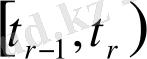үзіліссіз және 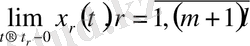сол жақты шегі бар болады, норма келесі түрде анықталған

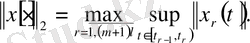
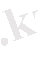
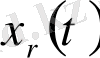арқылы 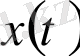функциясының 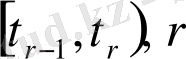аралығында сығылуын белгілейміз. 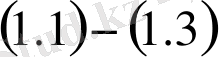есебін көпнүктелі импульсті шеттік есепке келтіреміз:

\

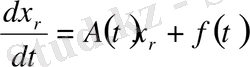
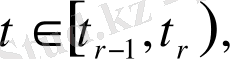
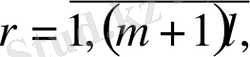
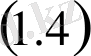
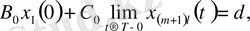
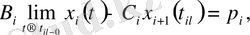
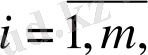
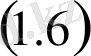
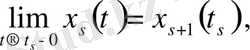
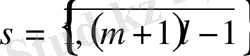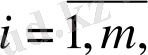
Импульсті түрткілі нүктелерден басқа, ішкі бөліктеу нүктелерінің
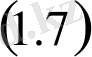
жабыстыру шарты 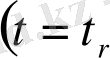нүктесінде 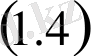теңдігін қанағаттандырсын).
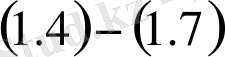есебінің шешімі
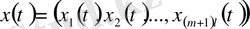
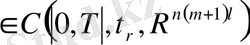функциялар жүйесін, келесі шарттарды қанағаттандыратын:
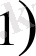
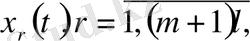функциясы үзіліссіз дифференциалданады. 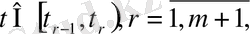болғанда 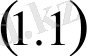дифференциалдық теңдеуін қанағаттандырады 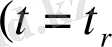нүктесінде 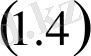теңдеуін қанағаттандырады );
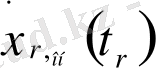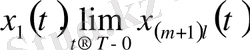мәндері үшін 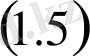теңдік, ал
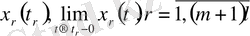мәндері үшін 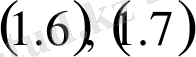теңдіктері орындалатынын айтамыз.
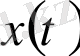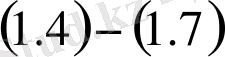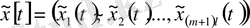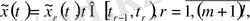
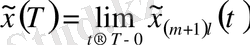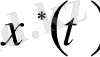Егер шешімі болса , онда оның сығылуы есебінің шешімі болады. Керісінше, егер есебінің шешімі болсын, онда теңдіктерімен анықталған функция бастапқы есептің шешімі болады. есебінің шешімі болсын, ал 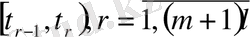аралығында 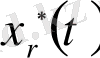оның сығылуы болады. 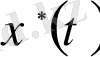функция 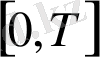бөліктенген үзіліссіздігінен сол жақты шегі бар екендігі шығады

\

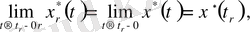
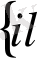
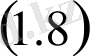
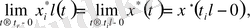
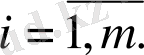
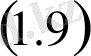
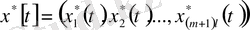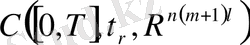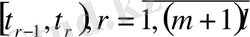Яғни, оның сығылу кеңістігінде жатыр. Сонымен қатар функциясы үзіліссіз дифференциалданады және 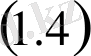дифференциалдық теңдеулер жүйесін қанағаттандырады:

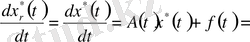
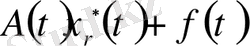
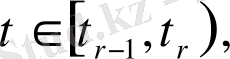
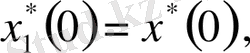
Сондықтан 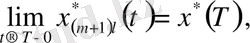теңдіктерінен 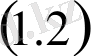шекаралық шартты ескеріп,

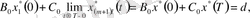
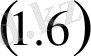импульсті түрткілі шарттың әсерінен
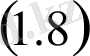қатынасынан: \
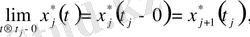
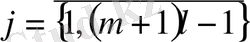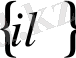
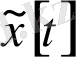
Сондықтан, 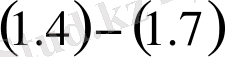есебінің шешімі болып табылады. Керісінше, 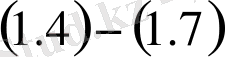есебінің шешімі 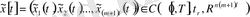болсын. 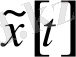элементінің теңдіктерінен:

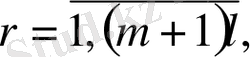
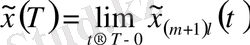
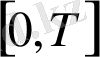аралығында 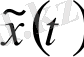функциясын анықтаймыз. 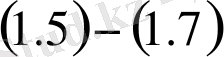ескеріп 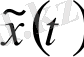, функциясы шеттік шартты қанағаттандырады:

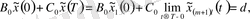
импульсті түрткілі шартты қанағаттандырады функциясы

импульсті түрткілі нүктелерінде бірінші текті нүктелері болуы мүмкін
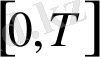
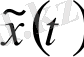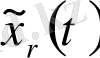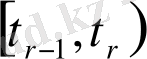
бөлікті үзіліссіз функция болып табылады. жүйесінің әрбір функциясы 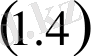дифференциалдық теңдеулер жүйесінің шешімі, онда
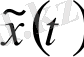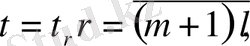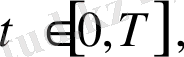
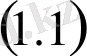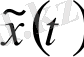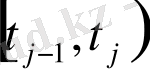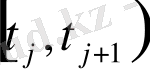
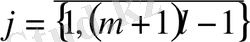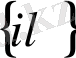
функциясының үзіліссіз туындысы бар және нүктелерінен басқа , барлық дифференциалдық теңдеуін қанағаттандырады функциясының нүктелерінде үзіліссіз туындысы, ал жағдайында сол жақты туындысы бар екендігін көрсетейік және \ 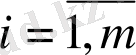интервалында 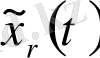функциясы үшін келесі теңдік орындалады:

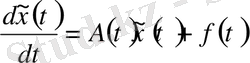
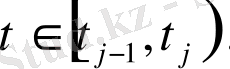
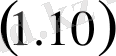
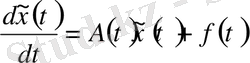
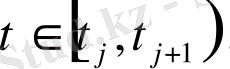
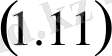
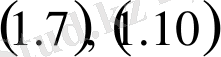теңдіктен 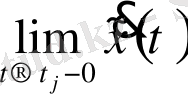шығады және

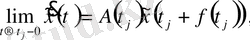
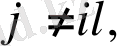
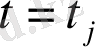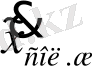
бар болады. нүктесінде 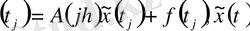функциясының сол жақты туындысы бар екендігі шығады. 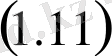және оң жақты туындысы бар екендігін ескере отырып

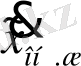
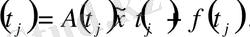
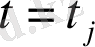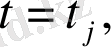
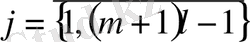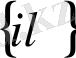
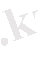
нүктесінде туындысының бар екендігін аламыз және \ нүктесінде 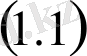дифференциалды теңдеулер жүйесі орындалады. 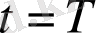нүктесінде сол жақ туындысының бар екендігі 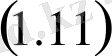шығады.
Сонымен біз анықтаған функциясы 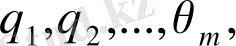нүктелерінде бірінші текті үзіліссіз болуы мүмкін 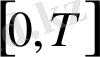аралығында бөлікті үзіліссіз 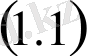дифференциалдық теңдеулер жүйесі және 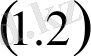шекаралық шарты 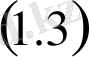импульсті түрткілі шартын қанағаттандыратын 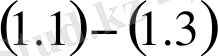есебінің шешімі болып табылады.
белгілеуін енгіземіз және әрбір интервалында алмастыруын енгіземіз. есебі эквивалентті параметр мен берілген көпнүктелі шектік есепке келеді:

\
есебінің шешімі элементтері болатын жұбы табылады, мұндағы функциясы үзіліссіз дифференциалдық функция және теңдігіне дифференциалдық теңдеулер жүйесі (1.13)-(1.16) шарттарын қанағаттандырады.
Егер жұбы
есебінің шешімі болса, онда

функциялар жүйесі есебінің шешімі болып табылады. Керісінше, егер есебінің шешімі болса, мұндағы онда жұбы есебінің шешімі болады. Алайда, есебінің есебінен айырмашылығы нүктесінде бастапқы шарт пайда болады.
Бұл шарт арқылы Вольтерра екінші текті интегралдық теңдеуінен анықтауға болады.

орнына есебінің сәйкес оң жағын қойып, үрдісті рет қайталап

Белгілеу енгізейік

функциясына келесі түріне келеміз:

есебінен табамыз:

сәйкес оң жақ бөлігін шарттарына қойып және сәйкес
көбейтіп, белгісіз параметріне байланысты теңдеулер жүйесін аламыз:

мұндағы I- бірлік матрица өлшемі болатын. арқылы сәйкес сол жақ бөлігінен матрицасын белгілеу арқылы келесі жүйені аламыз:

мұндағы,
Осылайша есептің шешімі жұбын табу үшін тұйықтеңдеулер жүйесі бар болады. Егер белгілі параметрлер онда интегралдық теңдеуден анықтаймыз. Және керісінше егер белгілі функция жүйесі , онда теңдеуінен параметрінің мәнін табамыз. Алайда сол сияқты белгісізболып табылады, сондықтан жұбын табу үшін тізбектеп жуықтау әдісін және келесі алгоритімді қолданамыз:
0-қадам. а) Айталық алынған бойынша қайтымды болсын делік, параметрі бойынша бастапқы жуықтауды теңдеуінен анықтаймыз, яғни
б) векторларының компаненті және Коши есебін шешу арқылы интервалында болғанда функциясы табылады.
1-қадам. а) Табылған функциясын теңдігінің оң жағына қойып, теңдеуден параметрі бойынша бірінші жуықтауы табылады;
б) , болғанда интервалында Коши есебін шешу арқылы табамыз, т.с.с.
k-қадамға дейін осы үрдісті қайталй отырып, жұптар жүйесін аламыз.
Тізбектерді жуықтау айырымында бағалау сондай-ақ тұжырымды дәлелдеу үшін Гронулла-Беллмана теңсіздігін қолданамыз. [86,c.108]
Гронулла-Беллман теңсіздігі. және болсын, болғанда, сонымен қатар келесі теңсіздік орындалады :

Мұндағы с оң тұрақты, онда болғанда келесі теңсіздікті аламыз :

Келесі ұсынылған теорема алгоритмнің бар болуы мен жалғыз шешімге жинақталуының жеткілікті шартын сондай-ақ нақты және жуық шешімдердің айырымын бағалауды көрсетеді.
Теорема 1. Кейбір және матрицасы қайтымды болсын және келесі теңсіздік орындалсын

Онда жұұптарының тізбегі есептің жалғыз шешіміне ұмтылады және келесі бағалау орынды:

Мұндағы

Дәлелдеуі. қайтымды болуынан және теңдіктен бар екендігі шығады және бағалайық:

Коши есебінің шешімі функциялары болғанда тізбектеп жуықтау әдісімен табамыз:

Импульсті түрткілі нүктелерде сол жақты шегін айқындап, кесіндісінде сәйкесінше теңсіздікті аламыз, мұндағы матрица, вектор функция:

үзіліссіздігінен

айырымы үшін

теңсіздік орынды.
функциясын анықтап , нүктесінде теңдігінен кесіндісі үзілісті функцияларын анықтаймыз. сегментіндегі үзіліссіздікті ескеріп, интегралдық функциялар теңдеуін

және шекке көшіп, оң жақты шегі

бар болады. Онда келесі бағалау орынды:

m-қадамды итерациялық үрдісті жалғастырып аламыз

бар болуынан, негізінде пара пар тұрғыдан бар болуын құрамыз

және

Осыдан,

функциялар жүйесінен тізбегі нормасы брйынша функциялар жүйесіне жинақталатын теңсіздіктен шығатыны анық. Кеңістіктің толықтығын ескере отырып,

функциялар жүйесін Гранулла-Беллман теңсіздігі бойынша келесі бағалауды қамтамасыз етеміз:

ескеріп аламыз:

Алгоритмнің бірінші қадамы бойынша келесі теңдеуден анықтаймыз:

т.с.с. және болғанда, нормасын бағалаймыз:

болғанда Коши есебінің шешімі

,

итерационды үрдісті қолданамыз

,

Яғни

Барлық сол жақ ақырлы шектер бар болғандықтан функциясын нүктесінде оның сол жақ шегін де анықтап, аралығында функциясын аламыз. болғанда үзіліссіздігінен шығады

нүктесінде теңдігі арқылы функциясының шегін анықтап бөлігінде үзіліссіз функциясын аламыз.
Онда бөлігінде теңдіктегі интеграл астыфункциялардың үзіліссіздігін ескеріп

және шегіне көшіп сол жақ шегінің бар еендігін аламыз.

ақырлы сол жақты шегі, барлық бар болады және нормаланған кеңістігінен функциялар жүйесінен жинақтылығынан , функциялар жүйесі құрылады.

Осы кеңістіктің тығыздалуынан функциялар жүйесі болады.
Коши есебінің шешімдерінің айырымын бағалайық:

Гронулла - Беллмана теңсіздігін қолданып

Итерационды үрдісті жалғастырып , жұбын мұндағы , табамыз, тағыда Гронулла - Беллман теңсіздігін қолданып Коши есебінің шешімдерінің парметрлерінің айырымын абағалайық:

Осыдан

теңдеуінің шешімі болса, сәйкес оң жақ бөлігінің нормаларының айырымдары үшін келесі теңдеу орынды

теңсіздігінің оң жақ бөлігіне орнына қойып, интегралды шығарып аламыз

шартының күшінде, , және теңсіздіктерінен тізбегінің , жинақталуынан және функциялар жүйесінің тізбегінен нормаланған кеңістігінен функциялар жүйесі жинақталады.
Кеңістіктің тығыздығын ескеріп , функциялар жүйесін аламыз.
Жалғыздығын дәлелдейік. Керісінше ұйғарып , есебінің жалғыз шешімі және бар болсын. Анологиялық тұрғыдан , құрамыз:

шартының күшінде, , теңдеудің орыныа сондай-ақ , барлық
үшін бар болады. Теорема 1 дәлелденді.
функциясын келесі теңдеумен анықтаймыз:

,

Теорема 2. Теорема 1 шарты орындалатын болсын. Онда есебінің жалғыз шешімі және келесі бағалау орынды.

орынды.

Теорема 3. Кейбір l және болсын,онда матрицасы қайтымды және теңсіздіктер орындалады.
Сонда импульсті түрткілі шетті есебінің жалғыз шешімі бар және ол үшін келесі бағалау орынды:

мұндағы

+

Дәлелдеуі. импульсті түрткілі көпнүктелі шеттік есебінің шешімі жұбы жалғыз екендігі теорема 1-де көрсетілген. есебінің есебіне эквивалентілігінен , шеттік есебі жалғыз шешімі бар болады, келесі теңдеумен анықталады

,

теңсіздігінен және бағалауынан болғанда теорема 2-ден дұрыстығын аламыз. Теорема 3 дәлелденді.
Теорманың ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.