Ықтималдық теориясы және математикалық статистика: орта кәсіптік білімге арналған оқу-әдістемелік құрал


ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
ТҮРКІСТАН ОБЛЫСЫНЫҢ АДАМИ ӘЛЕУЕТТІ ДАМЫТУ БАСҚАРМАСЫ
Ғ. МҰРАТБАЕВ АТЫНДАҒЫ ЖЕТІСАЙ ГУМАНИТАРЛЫҚ-ТЕХНИКАЛЫҚ КОЛЛЕДЖІ
«Математика және физика» кафедрасы
«Ықтималдықтар теориясы және математикалық статистика» пәнінен
ӘДІСТЕМЕЛІК ЖИНАҚ
Дайындаған: Н. Е. Ажибеков
ЖЕТІСАЙ - 2020
Әдістемелік құрал
Ғ. Мұратбаев атындағы Жетісай гуманитарлық - техникалық колледжінің «Математика және физика » кафедрасында талқыланып, оқу - әдістемелік кеңесінде бекітілді.
№ хаттама
«___» 2020ж
Пікір жазған:
Ғ. Мұратбаев атындағы Жетісай гуманитарлық - техникалық колледжінің директордың оқу ісі жөніндегі орынбасары педагогика ғылымының кандидаты: Баймаханова Л. А.
Дайындаған:
«Математика және физика » кафедрасының оқытушысы: Ажибеков. Н. Е
Әдістемелік құрал орта кәсіптік білім беретін оқу орындарының жас мамандары мен студенттеріне арналған.
Алғы сөз
« Ықтималдықтар теориясы және математикалық статистика» пәні - классикалық университеттердің математика және математикаға жақын бағыттар (информатика, механика, математикалық және компьютерлік модельдеу, ақпараттық жүйелер т. с. с. ) мамандықтары үшін мамандықтардың жалпыға міндетті білім стандарттарының оқытылуға міндетті пәндерінің құрамына кіретін іргелі математикалық пәндердің бірі. Бұл пән сонымен қатар көптеген жаратылыстану салалары, техникалық және экономикалық мамандықтар бойынша оқытылатын жоғары математика курсының аса маңызды бөліміне жатады, тіпті, кейбіреулері (әсіресе, жаңа экономикалық бағыттардағылары) үшін бірегейі де болып табылатыны.
Жаңа түсініктеме элементар оқиғалар кеңсітігі, Оқиға, А және В оқиғаларының қосындысы, көбейтіндісі, Ықтималдықтың классикалық анықтамасы, Ықтималдық аксиомалары, А оқиғасының В оқиғасы пайда болғандағы ықтималдығы, А және В оқиғалары тәуелсіз, Толық ықтималдық формуласы, Байес формуласы, Бернулли сұлбасы, Қарастырылып отырған оқиға
п
тәжірибеде
т
рет пайда болу ықтималдығы, Кездейсоқ шама, Дискретті кездейсоқ шама, Дискретті кездейсоқ шаманың математикалық үміті, Дискретті кездейсоқ шаманың дисперсиясы, Кездейсоқ шаманың ықтималдық үлестірімінің интегралдық функциясы, Үзіліссіз кездейсоқ шама, Ықтималдықтың үлестірім тығыздығы, Үзіліссіз кездейсоқ шаманың математикалық үміті, дисперсиясы,
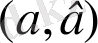 аралығындағы бірқалыпты үлестірім ықтималдығы, Х кездейсоқ шаманың қалыпты үлестірім тығыздығы, Чебышев теңсіздігі, үлкен сандар заңы. Чебышев теоремасы, Бас жиынтық, Таңдама жиынтығы, жиынтық көлемі, Вариациялық қатар, Салыстырмалы жиілік, Таңдаманың , Бас орта (таңдаулы орта), Бас дисперсия
аралығындағы бірқалыпты үлестірім ықтималдығы, Х кездейсоқ шаманың қалыпты үлестірім тығыздығы, Чебышев теңсіздігі, үлкен сандар заңы. Чебышев теоремасы, Бас жиынтық, Таңдама жиынтығы, жиынтық көлемі, Вариациялық қатар, Салыстырмалы жиілік, Таңдаманың , Бас орта (таңдаулы орта), Бас дисперсия
 . Бас орта квадраттық ауытқу
. Бас орта квадраттық ауытқу
 , Таңдаулы дисперсия
, Таңдаулы дисперсия
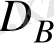 . Ығыстырылған дисперсия (эмпирикалық) дисперсия
. Ығыстырылған дисперсия (эмпирикалық) дисперсия
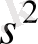 ., Белгісіз параметр
., Белгісіз параметр
 -ның
-ның
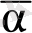 бағасының сенімділік интервалы қарастырылады.
бағасының сенімділік интервалы қарастырылады.
Пререквизиттер :
-Математикалық анализ
-Алгебра және геометрия
-Жиындар теориясы
- ғылыми көзқарас пен логикалық ойлау қабілетін қалыптастыру
Постреквизиттер:
«Ықтималдықтар теориясы және математикалық статистика» - практикалық есептері комбинаторикалық әдістерді қолдану арқылы шешуге болатыны және болашақ мамандарға негізгі математикалық білім беретін пән- кездейсоқ оқиғалардың заңдылықтарын қарастыратыны ескертіледі.
Осы пәннің әдістері практиканаң сан алуан салаларында кеңінен қолданылып, физика, химия, биология құбылыстарының, техника мен экономика процестерінің заңдылықтарын жан - жақты және терең түсінуге орасан зор ықпалын тигізуде.
Пәннің мақсаты: Математикалық талдаудың моделдеуі және ғылыми негізін кездейсоқ оқиғалар мен процесстерде олардың сипаттамалық қасиеттерін үйретуде студенттердің білімін қалыптастыру.
Пәннің міндеті:
- ықтималдықтар теориясы мен матматикалық статистиканың негізгі ұғымдары мен заңдылықтарын және олардың түрлі салаларда қолданын зерттеу;
- нақтылы есептерді шешу тәсілдері мен әдістерін меңгеру;
- табиғи процестердің математикалық модельдерін түзе және түзілген модельді сынақтау тәсілдерін таңдай білу;
- ғылыми және ақпаратты әдебиеттерді пайдалана білу;
- математикалық интуицияны дамыту;
- математикалық мәдениеттілікті тәрбиелеу.
Студенттер білуі керек: Ықтималдықтар теориясы және математикалық статистиканың негізгі ұғымдары мен заңдылықтарын еркін қолдануға;
- математикалық есептерді қоя білуге;
- ықтималдықтар модельдерін құра білуге;
- қолайлы ықтималдық тәсілдерді және есеп шешімінің алгоритімін таңдай алуға;
- сапалы статистикалық зерттеулер жүргізуге;
-жүргізілген талдаулар негізінде қолдануға қажетті және тиімді іс жүзінде нұсқаулар ұсынуға- міндетті.
М. В. Ломоносов атындағы Мәскеу мемлекеттік университетінің механика-математика факультетінің ықтималдықтар теориясы кафедрасын басқарған аса көрнекті математик, тамаша педагог Б. В. Гнеденконың бұрынғы КСРО ғана емес, басқа да көптеген әлем елдерінің студент жастарының ықтималдықтар теориясын оқып үйренуіне негіз болған « Ықтималдықтар теориясы курсы » атты оқулығының 6-басылымының алғы сөзінде жазған "Мен математикалық пәндермен, әсіресе ықтималдықтар теориясымен алғашқы танысыу кезінде өзіндік теориялық-ықтималдықтық интуицияны, абстрактылы идеялар мен әдістерді практикалық жағдайлармен ұштастыру қабілетін дамытуға көмектесетін көптеген мысалдарды қарастыру қажет деп есептеймін. Бұл жетістік әрбір математикке, әсіресе қолданбалылық бағыттағы ғылыми-зерттеу институттарында жұмыс істеу күтіп тұрған математик студенттердің басым көпшілігіне қажет. Оның үстіне бүгінгі күні көптеген мамандар ықтималдықтар теориясымен танысуға мәжбүр, өйткені олардың күнделікті жұмысында теориялық-ықтималдықтық концепциялар аса қажет" деген ой - пікірін еске ала отырып іске кіріс.
Педагогика ғылымының кандидаты: Баймаханова. Л. А
Мазмұны
- Алғы сөз . . . 3
- Дәріс оқулар . . . . . 7
- Практикалық сабақтар . . . . . . 61
- Студенттің өздік жумысы . . . . . . 74
- Пайдалынылған әдебиет тізімі . . . 83
2 ДӘРІС ОҚУЛАР
Дәріс сабақтардың құрылымы
1-дәріс. . Комбинаторика элементтері.
- Комплексті шарт, сынау, оқиға, жағдайлар
2. Оқиғалар классификациясы
3. Ықтималдықтың классикалық анықтамасы
1 Комплексті шарт, сынау, оқиға, жағдайлар
Бұл ұғымдарды түсіндіру үшін мысалға жүгінейік.
Мысал. Біртектес материалдан жасалған симметриялы дұрыс кубтың әрбір жағын 1-ден 6-ға дейінгі цифрлармен нөмірлейік. Оны бір рет лақтырғанда (комлексті шарт орындалғанда) 6 жағының бірі жоғары қарап түседі? Қай жағы (нөмері) түссе де мұнымыз оқиға болады.
Комплексті шарт деген терминнің орнына сынау , тәжірибе, эксперимент терминдерін де пайдаланады. Біз көбінесе сынау терминін қолданатын боламыз. Бұдан былай сынау нәтижесін оқиға деп түсінетін боламыз. Әдетте оқиғаларды А, В, С, . . . бас әріптерімен белгілейді.
Сынау кезінде бірі пайда болғанда, екіншісі пайда болмайтын нәтижелерді (оқиғаларды) жағдайлар дейміз. Оларды А 1 , А 2 , . . . , А п әріптерімен белгілейміз. Осы сыналатын жағдайлардың барлық (жалпы) санын п -мен белгілейміз. Мысалы, тенгені лақтырғанда жағдайлар саны n =2, ал кубты лақтырғандағы жағдайлар саны n =6 болады.
2. Оқиғалар классификациясы
Сынау жүргізілгенде А оқиғасы пайда болуы да, пайда болмау да мүмкін болса, ондай оқиғаны кездейсоқ оқиға дейді. Сынау нәтижесінде оқиға ( А оқиғасы) сөзсіз пайда болатын болса, ондай оқиғаны ақиқат оқиға дейді. Сынау нәтижесінде оқиға ( А оқиғасы) сөзсіз пайда болмайтын болса, ондай оқиғаны мүмкін емес оқиға дейді.
Сынау жүргізгенде оқиғаның бірі пайда болғанда, екіншісі пайда болмайтын екі оқиғаны үйлесімсіз оқиғалар дейді.
Кез келген екі-екіден алынған оқиғалар үйлесімсіз болса, ондай оқиғаларды қос-қостан үйлесімсіз дейді.
Сынау жүргізгенде оқиғаның бірі пайда болғанда, екіншісінің де пайда болуы мүмкін болатын екі оқиғаны үйлесімді оқиғалар деп атайды. Мысалы, кубтың жұп нөмірінің шығуы ( А оқиғасы) және үш санына еселік нөмірдің шығуы ( В оқиғасы) үйлесімді. Өйткені кубтың 6-нөмірінің шығуын көрсететін А 6 оқиғасы А оқиғасы пайда болғанда да, В оқиғасы пайда болғанда да пайда болуы мүмкін.
Сынау нәтижесінде оқиғалардың тек әйтеуір біреуінің сөзсіз пайда болуы ақиқат болса, ондай оқиғаларды жалғыз ғана мүмкіндікті оқиғалар дейді. Мысалы, сынау нәтижесінде кубтың алты жағының біреуі ( А оқиғасы) шығуы сөзсіз, сондықтан А 1 , А 2 , . . . , А 6 оқиғалары жалғыз ғана мүмкіндікті оқиғалар, бұлар оқиғалардың толық тобын құрайды деп атайды. Сондықтан бұл оқиғалар қос-қостан үйлесімсіз және оқиғалардың толық жүйесін құрайды.
. 3. Ықтималдықтың классикалық анықтамасы
Жоғарыда біз оқиға түрлеріне мысалдар келтірдік, енді оқиғаның пайда болуы мүмкіндігінің сандық өлшеуішін көрсетеміз. Жалпы айтқанда, А оқиғасының пайда болу мүмкіндігінің сандық мөлшеріне р(А) функциясының мәні алынады. Мұны осы А оқиғасының ықтималдығы деп атайды.
Қандай болмасын математикалық теория белгілі бір ұғымдар негізінде құралатын болғандықтан, біз ықтималдықтар теориясының құрылуын ықтималдықтың классикалық анықтамасына негіздейміз.
Ықтималдықтың классикалық анықтамасын алғаш рет берген Лаплас еді.
Ықтималдықтың классикалық анықтамасы оқиғалардың тең мүмкіндіктеріне (тең ықтималдығына) сүйенеді.
Тең мүмкіндік немесе тең ықтималдық ұғымдары алғашқы ұғымдарға жатады, олар логикалық (формальді) анықтама беруді қажет етпейді. Жалпы сынау нәтижесінде бірнеше оқиғалар пайда болуы мүмкін болса және олардың біреуінің пайда болуы мүмкіндігінің, екіншісіне қарағанда, артықшылығы бар деп айта алмайтын болсақ, яғни сынаулар нәтижесінің симметриялы қасиеті болса, мұндай оқиғалар тең мүмкіндікті делінеді.
Бірнеше оқиғалар тең мүмкіндікті, қос-қостан үйлесімсіз және оқиғалардың толық тобын құраса, онда ол оқиғаларды сынаудың мүмкін нәтижелерінің толық тобы деп атайды. Бұл терминнің орнына тең мүмкіндікті барлық жағдайлар немесе жалпы жағдайлар саны не, қысқаша жағдайлар деп атайды.
Ал тең мүмкіндікті үйлесімсіз және оқиғалардың толық тобын құрайтын оқиғалардың (жағдайлардың) бірнешеуі бір А оқиғасының пайда болуын тудыруы мүмкін. Бұл оқиғаларды қолайлы жағдайлар деп атайды.
Анықтама. А оқиғасы қолайлы жағдайлар санының ( т ) сынаудың тең мүмкіндікті барлық жағдайлар санын ( п ) қатынасын А оқиғасының ықтималдығы деп атайды және былай жазады:
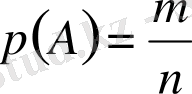 (1)
(1)
Ықтималдықтың бұл анықтамасын классикалық анықтама дейміз. Бұдан төмендегі салдар шығады.
- Ақиқат оқиға ықтималдығы 1-ге тең.
Шынында, оқиға ақиқат болу үшін А оқиғасына қолайлы жағдайлар саны т сынаудың барлық тең мүмкіндікті жағдайлар саны п -ге тең, яғни m=n болады. Онда (1) бойынша
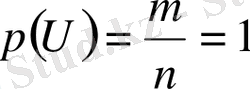 (2)
(2)
- Мүмкін емес оқиға ықтималдығы нөлге тең.
Шынында да, егер оқиға мүмкін емес болса, онда А оқиғасына қолайлы жағдайлар саны т нөльге тең болады. Олай болса
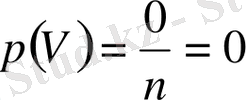 (3)
(3)
3. А оқиғасының ықтималдығы р(А) нөль мен бір аралығындағы оң таңбалы сан. Шынында, А оқиғасына қолайлы жағдайлар саны т нөльден п -ге дейінгі, өздерін қоса алғандағы, мәндерді қабылдайды, яғни
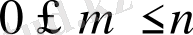 ,
,
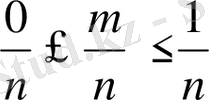 немесе
немесе
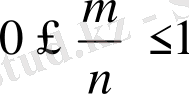
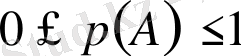 (4)
(4)
2 дәріс. Кездейсоқ оқиғалар. Ықтималдықтың классикалық анықтамасы.
Ықтималдықтарды тікелей есептеуге мысалдар
2. Қосу теоремасы
3. Қосудың кеңейтілген теоремасы
2 Ықтималдықтарды тікелей есептеуге мысалдар
1-мысал. Жәшікте 3 ақ шар, 5 қызыл шар, 2 жасыл шар бар. Бұл шарлардың формасы және салмағы бірдей. Жәшіктен кез келген бір шар алынды. Алынған шар: а) ақ шар ( А оқиғасы), ә) қызыл шар ( В оқиғасы), б) жасыл шар ( С оқиғасы) болу ықтималдығын анықтау керек.
Шешуі: Шарлардың үлкендігі мен салмағы бірдей болғандықтан, олардың шығу мүмкіндіктері де бірдей. Бір түсті шар шыққанда екінші түсті шар пайда болмайды. Сонымен, тең мүмкіндікті қос-қостан үйлесімсіз оқиғалардың толық тобын құрайтын жағдайлар саны n =10. А оқиғасына қолайлы жағдайлар саны m= 3. Демек,
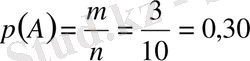 немесе 30% болады.
немесе 30% болады.
ә)
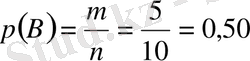 немесе 50% болады.
немесе 50% болады.
б)
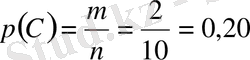 немесе 20% болады.
немесе 20% болады.
2-мысал. Монета екі рет лақтырылды. Кем дегенде бір рет герб жағы пайда болуы ықтималдығын анықтау керек.
Төменгі тең мүмкіндікті 4 жағдай болады. Олар: ГТ, ТГ, ГГ, ТТ.
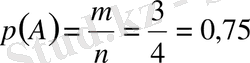 немесе 75% болады.
немесе 75% болады.
3-мысал. Бірден екі ойын кубы лақтырылады. Екі куб еденге түскенде шыққан нөмірлерінің қосындысы 7 болуы ықтималдығы неге тең?
Шешуі: Барлық мүмкін жағдайларды есептейік. Бірінші куб жақтарының нөмірлері әр түрлі алты тәсілмен түсуі мүмкін. Бұлар әр жолы екінші кубтың алты нөмірінің бірімен комбинацияланады. Сонда n =6⋅6=36 болады. Қолайлы жағдайлар саны: 1+6=7, 2+5=7, 3+4=7, 4+3=7, 5+2=7, 6+1=7
m=
6.
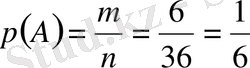 .
.
Қосу теоремасы
Ықтималдықтарды есептеу сынаудың жалпы саны мен оқиғаның пайда болуына қолайлы нәтижелер санын анықтауға келіп тіреледі. Бұларды тікелей есептеу көп жағдайда үлкен қиындыққа ұшыратады. Оның үстіне, практикада кездесетін оқиғалар күрделі болып келеді де, олардың ықтималдығын табу үшін, ол оқиғаларды бірнеше қарапайым оқиғалардың қосындысы не көбейтіндісі түрінді жазып, солардың ықтималдықтары арқылы күрделі оқиға ықтималдығын анықтайды. Ол үшін негізінен ықтималдықтарды қосу және көбейту теоремаларын пайдаланады.
Қосу теоремасы . Үйлесімсіз А және В оқиғаларының қосындысының ықтималдығы олардың ықтималдықтардың қосындысына тең, яғни
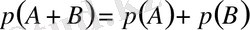 (1)
(1)
Д/уі: Теореманы дәлелдеу үшін (1) теңдіктегі үш ықтималдықты есептеп, ол мәндерді (1) теңдікке қойып, оның дұрыстығына көз жеткізу жеткілікті.
Қосудың кеңейтілген теоремасы
Егер А 1 , А 2 , . . . , А п қос-қостан үйлесімсіз оқиғалар болса, онда бұлардың қосындысының ықтималдығы олардың әрқайсысының ықтималдықтарының қосындысына тең болады, яғни
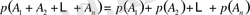 (2)
(2)
1-салдар. Оқиғалардың толық тобын құрайтын қос-қостан үйлесімсіз сынау нәтижелері ықтималдықтарының қосындысы бірге тең.
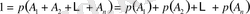
2-салдар. Қарама-қарсы екі оқиға ықтималдықтарының қосындысы бірге тең, яғни
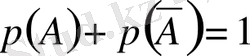 .
.
3 дәріс. Қосу және көбейту теоремалары.
1. Тәуелсіз және тәуелді оқиғалар.
2. Шартты ықтималдық
3. Ықтималдықтарды көбейту теоремасы
1 Тәуелсіз және тәуелді оқиғалар.
Егер екі оқиғаның бірінің пайда болуы екіншісінің пайда болу ықтималдығын өзгертпесе, ондай екі оқиғаны тәуелсіз деп атайды.
Егер екі оқиғаның бірінің пайда болуы екіншісінің пайда болу ықтималдығын өзгертетін болса, ондай оқиғаны тәуелді оқиғалар деп атайды.
А
оқиғасының пайда болуы
В
оқиғасының пайда болуына байланысты, яғни
А
оқиғасының пайда болу ықтималдығы
В
оқиғасының пайда болуына байланысты өзгереді. Мұндай ықтималдықты шартты ықтималдық деп атайды. Шартты ықтималдықты былай белгілейді:
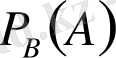 -
В
оқиғасы орындалғанда
А
оқиғасының пайда болу ықтималдығы.
-
В
оқиғасы орындалғанда
А
оқиғасының пайда болу ықтималдығы.
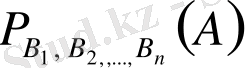 -
-
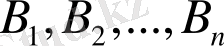 оқиғалары орындалғанда
А
оқиғасының пайда болу ықтималдығы.
оқиғалары орындалғанда
А
оқиғасының пайда болу ықтималдығы.
3 Ықтималдықтарды көбейту теоремасы
Теорема. Екі тәуелді оқиға көбейтіндісінің ықтималдығы біреуінің шартсыз ықтималдығын сол оқиға пайда болды деп алынғандағы екінші оқиғаның шартты ықтималдығына көбейткенге тең:
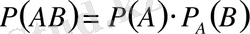 (1)
(1)
немесе
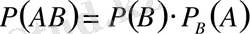 (1
/
)
(1
/
)
Мысал. М О С К В А сөзін құрастыратын кеспе әріптер әбден араластырылып, 4 кеспе әріпті қатарынан қойғанда К В А С сөзінің шығу ықтималдығын анықтау керек.
Шешуі: Бірінші алынған кеспе әріп К болуы А 1 оқиғасы болсын, екіншісі В болуы - А 2 , үшіншісі А болуы - А 3 , төртіншісі С болуы А 4 оқиғасы болсын десек, онда КВАС сөзінің пайда болуы А оқиғасы болады. Көбейту теоремасы бойынша
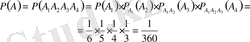
болып шығады.
Теорема . Екі тәуелсіз оқиғалар көбейтіндісінің ықтималдығы олардың шартсыз ықтималдықтарының көбейтіндісіне тең, яғни
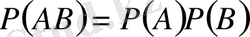
болады.
4 дәріс . Ең болмағанда бір оқиғаның пайда болуының ықтималдығы
1. Ықтималдықтарды қосудың жалпы теоремасы
2. Ықтималдықтың толық (орта) формуласы
3. Байес формуласы
1. Ықтималдықтарды қосудың жалпы теоремасы
Теорема. Екі оқиғаның кемінде біреуінің пайда болу ықтималдығы олардың ықтималдықтарының қосындысынан оқиғалардың бірден пайда болу ықтималдығын шегерткенге тең болады.
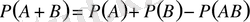 (1)
(1)
Мысал. Колодада 36 карта бар. Кездейсоқ алынған бір картаның көзір немесе тұз болу ықтималдығын анықтау керек.
Шешуі: Шыққан картаның көзір болуы А оқиғасы, тұз болуы В оқиғасы болсын. Сонда көзір тұздың шығуы АВ оқиғасы болады. Мұның ықтималдығы
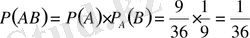
А және В оқиғалары үйлесімді, өйткені көзір карта тұз болуы да мүмкін. Олай болса,
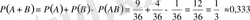
немесе 33, 3%, өйткені
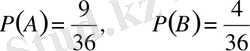
2. Ықтималдықтың толық (орта) формуласы
Айталық,
Н
1
, Н
2
, . . . , Н
п
оқиғалары қос-қостан үйлесімсіз оқиғалардың толық тобын құрайтын болсын. Ал
В
оқиғасы осы оқиғалардың тек біреуімен ғана бірігіп орындалады дейік. Оның үстіне
р(Н
1
), р(Н
2
), . . . , р(Н
п
)
және
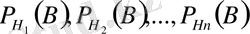 ықтималдықтары белгілі болсын. Осы берілгендер бойынша
В
оқиғасының ықтималдығын анықтауға бола ма және ол неге тең деген сұрақ туады. Мұның жауабын ықтималдықтың толық формуласы береді.
ықтималдықтары белгілі болсын. Осы берілгендер бойынша
В
оқиғасының ықтималдығын анықтауға бола ма және ол неге тең деген сұрақ туады. Мұның жауабын ықтималдықтың толық формуласы береді.
Шынында,
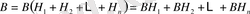 (1)
(1)
Ал
Н
1
, Н
2
, . . . , Н
п
қос-қостан үйлесімсіз болғандықтан,
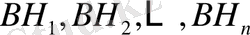 оқиғалары да қос-қостан үйлесімсіз. Олай болса, бұл оқиғаларға қосу теоремасын қолдануға болады. Сонда
оқиғалары да қос-қостан үйлесімсіз. Олай болса, бұл оқиғаларға қосу теоремасын қолдануға болады. Сонда
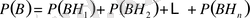
шығады.
Көбейту теоремасы бойынша
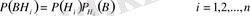
болады.
Демек,
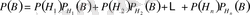
немесе
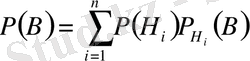 (2)
(2)
жоғарыдағы берілгендері бойынша В -нің ықтималдығын осы (2) формуламен анықтайды. Бұл формуланы ықтималдықтардың толық формуласы деп атайды. Әдетте, Н 1 , Н 2 , . . . , Н п оқиғаларын гипотезалар (болжамдар) деп атайды.
Байес формуласы
Осы уақытқа дейін қарастырып келген ықтималдықтар интуитивті түрде теориялық болжамдарға сүйеніп, тәжірибе жүргізбей-ақ, комплекс шарт жөніндегі білім (түсінік) негізінде анықталып келді. Тәжірибеге дейінгі Н 1 , Н 2 , . . . , Н п гипотезалар (оқиғалар) ықтималдығы сәйкес түрде р(Н 1 ), р(Н 2 ), . . . , р(Н п ) болатынды.
Тәжірибе жүргізілді делік, соның нәтижесінде
В
оқиғасының пайда болғаны анықталды, енді осы
В
оқиғасының пайда болуына байланысты
Н
1
, Н
2
, . . . , Н
п
гипотезаларының ықтималдығын қайта қарауға тура келеді. Яғни
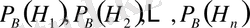 ықтималдықтар мәнін анықтауға тіреледі. Бұл ықтималдықты анықтау үшін, көбейту теоремасы мен ықтималдықтардың толық формуласын пайдаланамыз.
ықтималдықтар мәнін анықтауға тіреледі. Бұл ықтималдықты анықтау үшін, көбейту теоремасы мен ықтималдықтардың толық формуласын пайдаланамыз.
Тәуелді оқиғалар В мен
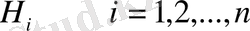 үшін
үшін
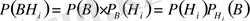 (1)
(1)
Бұдан
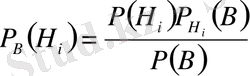 (2)
(2)
шығады. Бұл формулаға толық ықтималдық формуласынан
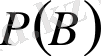 мәнін қойсақ, онда
мәнін қойсақ, онда
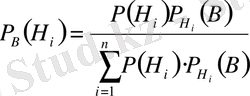 (3)
(3)
шығады. Осы (3) формуланы Байес формуласы деп айтады.
5 дәріс. Толық ықтималдық формуласы. Байес формуласы
- Сынауды қайталау
2.
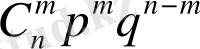 -нің жуық формуласы
-нің жуық формуласы
3. Муавр-Лапластың интегралдық теоремасы
Сынауды қайталау
Ықтималдықтар теориясы мен оның қолданылуында осы уақытқа дейін қарастырылып келген жеке сынау нәтижесінің іс тұрғысынан қарағанда қажеттігі шамалы. Өйткені практика жүзінде жеке сынау нәтижесін алдын-ала болжау мақсат етілмейді. Мұның орнына сынаудың сан алуан қайталанып отыратын жағдайы мен осыған тиісті ықтималдықтарды есептеуді мақсат етеді. Осы айтылғандарды жай мысалдармен түсіндірейік.
Сынау жүргізгенде бірнеше нәтиженің пайда болуын күтуімізге болады. Бұлардың ішіндегі ең қарапайым сынау нәтижесі тек екі оқиға.
А
және оған қарама-қарсы
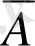 болатын және әрбір тәуелсіз сынауда оқиғаның пайда болу ықтималдығы тұрақты
болатын және әрбір тәуелсіз сынауда оқиғаның пайда болу ықтималдығы тұрақты
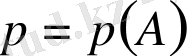 (пайда болмауы
(пайда болмауы
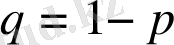 ) тең болатын схемасы. Мұндай қарапайым схеманы тұңғыш қарастырған Швецаря ғалымы Я. Бернулли (1654-1705), сондықтан бұл схеманы Бернулли схемасы немесе тәуелсіз сынауларды қайталау схемасы деп атайды.
) тең болатын схемасы. Мұндай қарапайым схеманы тұңғыш қарастырған Швецаря ғалымы Я. Бернулли (1654-1705), сондықтан бұл схеманы Бернулли схемасы немесе тәуелсіз сынауларды қайталау схемасы деп атайды.
Мысал. Нысананы көздеп 3 рет оқ атылды. Әрқайсысының дәл тию ықтималдығы бірдей, яғни ол
 -ге тең. Нысанаға дәл екі оқтың тию ықтималдығы неге тең.
-ге тең. Нысанаға дәл екі оқтың тию ықтималдығы неге тең.
Шешуі: Оқтың нысанаға тиюуі
А
десек, тимеуі
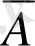 оқиғасы болады. Олардың ықтималдығы берілген шарт бойынша
оқиғасы болады. Олардың ықтималдығы берілген шарт бойынша
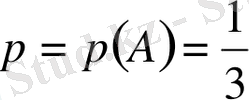
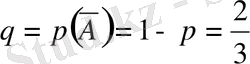
Оқтың екі рет дәл тиюуі В оқиғасы болсын. Әрине, бұл күрделі оқиға.
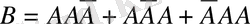
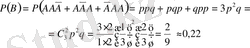
Теорема . Егер әрбір сынауда оқиғаның пайда болу ықтималдығы тұрақты және ол р -ге тең болса, онда п рет тәуелсіз сынау жүргізгенде ол оқиғаның дәл т рет пайда болу ықтималдығы мынаған тең:
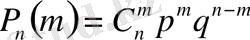 .
.
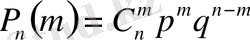 формуласын ықтималдықтардың биномдық үлестірімділігі не биномдық үлестірімділік заңы деп атайды.
формуласын ықтималдықтардың биномдық үлестірімділігі не биномдық үлестірімділік заңы деп атайды.
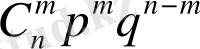 -нің жуық формуласы
-нің жуық формуласы
Сынау саны
п
үлкен болған сайын
 ықтималдықта Бернулли формуласымен есептеу қиындай түседі. Сондықтан ғалымдар осы формула жарық көрісімен-ақ, оған жуық формулаларды іздестіре бастаған.
п
жеткілікті үлкен болғанда, ол
р
мәні 0 мен 1-ге мейілінше жуық болмаған жағдайда төмендегі формуланы пайдаланады:
ықтималдықта Бернулли формуласымен есептеу қиындай түседі. Сондықтан ғалымдар осы формула жарық көрісімен-ақ, оған жуық формулаларды іздестіре бастаған.
п
жеткілікті үлкен болғанда, ол
р
мәні 0 мен 1-ге мейілінше жуық болмаған жағдайда төмендегі формуланы пайдаланады:
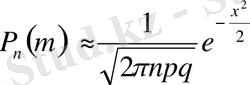 (1)
(1)
мұнда
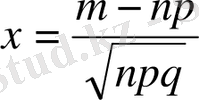 (2)
(2)
- жуық мәнін табу өте оңай. Ол үшін
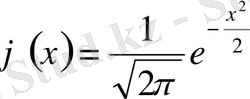 (3)
(3)
функциясының кестесін пайдаланамыз. (1-қосымша)
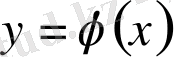 функциясы симметриялы, яғни
функциясы симметриялы, яғни
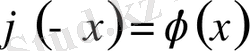 болғандықтан, кестеде
х
-тің оң мәндері ғана келтірілген. Сонымен, (1) формула
болғандықтан, кестеде
х
-тің оң мәндері ғана келтірілген. Сонымен, (1) формула
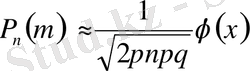 (4)
(4)
түрінде жазылады.
Муавр-Лапластың интегралдық теоремасы
Муавр-Лапластың теоремасы. Егер әрбір сынауда оқиғаның пайда болу ықтималдығы тұрақты және ол
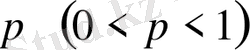 болса, онда сынау саны
болса, онда сынау саны
 жағдайда оқиғаның орындалу санының
жағдайда оқиғаның орындалу санының
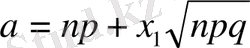 және
және
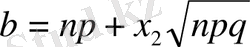 аралығында болу ықтималдығы
аралығында болу ықтималдығы
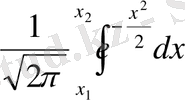
интегралына ұмытылады, яғни
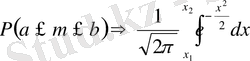 (5)
(5)
болады, мұндағы
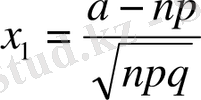 ,
,
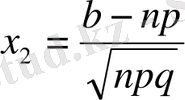
(5) теңдіктің оң жақ бөлігіндегі интеграл элементар функциялар арқылы есептелмейді. Сондықтан мына Лаплас функциясын енгіземіз:
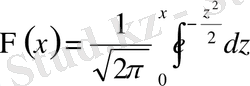 (6)
(6)
Бұл функцияның таблицасы кітап соңында беріледі. (2-қосымша) . Мұның қасиетін пайдалану арқылы (5) теңдікті ықшам түрде былай жазамыз:
 (7)
(7)
немесе
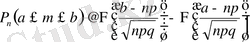 (7
/
)
(7
/
)
Мұны Лапластың интегралдық формуласы дейміз.
Лаплас функциясының мынадай қасиеттері бар.
1.
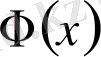 функциясы тақ функция, яғни
функциясы тақ функция, яғни
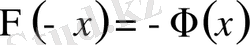 .
.
2.
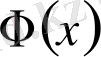 функциясы монотонды өспелі, яғни
функциясы монотонды өспелі, яғни
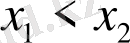 болса, онда
болса, онда
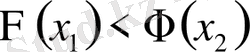 болады.
болады.
3.
х
шектеусіз өскенде
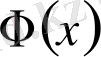 функциясы 0, 5-ке ұмтылады, яғни
функциясы 0, 5-ке ұмтылады, яғни
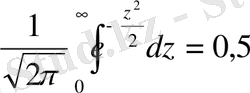 болады. Сондықтан
болады. Сондықтан
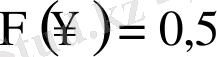 .
.
4.
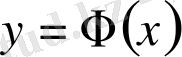 қисығы координаталар бас нүктесіне қатысты симметриялы. Мұның екі горизонтал асимптотасы бар, өйткені
қисығы координаталар бас нүктесіне қатысты симметриялы. Мұның екі горизонтал асимптотасы бар, өйткені
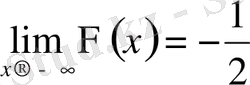 ;
;
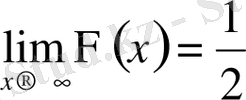 . Ал
. Ал
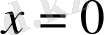 болғанда
болғанда
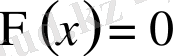 .
.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz