Ньютон формуласы

Қарастырылатын сұрақтар (дәріс жоспары) :

1. Қателіктер теориясы.
2. Қателіктердің жіктелуі.
3. Арифметикалық амалдар нәтижелерінің қателіктері.

Дәрістің қысқаша мазмұны:

Есептеу кезінде анализдік әдістерді пайдалану қиындық келтіргенде немесе тіпті пайдалану мүмкін болмаған жағдайда есептеу математикасының сандық әдістері қолданылады. Ол әдістер бастапқы берілген есепті мағынасы бойынша соған жуық басқа есеппен алмастыру мүмкіндігіне негізделген. Ал соңғы есеп кейбір шарттарды қанағаттандыруы тиіс. Мәселен, шешімінің бар болуы, орнықты, жинақты болуы және т. с. с. Бұл есептің шешімі алғашқы есептің жуық шешімін беруі тиіс немесе оған белгілі бір дәлдікпен жинақталуы қажет.

Дәл шешім мен жуық шешім айырмасы әдіс қателігі немесе дөңгелектеу қателігі деп аталады.

Қателіктер 3 түрге бөлінеді:

1. . Әдіс қателігі;
2. . Жөнделмейтін (түзетілмейтін) қателік;
3. . Есептеу қателігі.

Әдіс қателігі берілген есепті шешу үшін таңдалған сандық әдістен тәуелді болады. Осыған байланысты әр әдістің қателігін бағалау формуласы әртүрлі болады.

Жөнделмейтін (түзетілмейтін) қателіктер - есептің бастапқы берілгендерінен, коэффициенттерінен, шарттарынан тәуелді қателіктер.

Есептеу қателігі жуық шешімдерді алу барысында қолданылатын математикалық есептеулер кезінде қолданылатын сандарды дөңгелектеуден тәуелді.

Егер x саны - дәл мән, x ^* саны оған белгілі жуықтау болса, онда жуықтаудың абсолютті қателігі деп 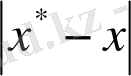- олардың айырымын, ал шектік абсолютті қателігі деп мына шартты қанағаттандыратын қателікті айтады: .

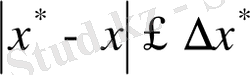Жуықтаудың салыстырмалы қателігі деп келесі шартты қанағаттандыратын шартты айтады:

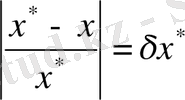немесе .

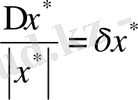Санның мәнді цифрлары деп оның жазылуындағы солдан бастағанда нөлден өзгеше барлық цифрларын айтады.

Мәнді цифрды дұрыс дейді, егер санның абсолютті қателігі осы цифрге сәйкес разряд бірлігінің жартысынан аспаса, кері жағдайда күмәнді цифр деп атайды.

Арифметикалық амалдар нәтижелерінің қателіктері:

1. Қосындының қателіктері. F(x) =x=x ₁ +x ₂ +x ₃ +…+x _n қосындысы берілсін.

a) қосындының абсолютті қателігі: .

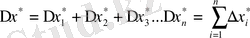Егер 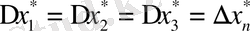болса, онда 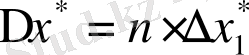, ал n>=10 болса, Чеботарев формуласы қолданылады: .

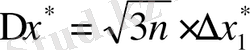b) қосындының салыстырмалы қателігі:

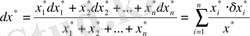. Мұндағы , , .

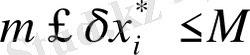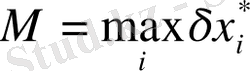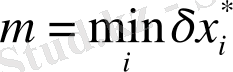2. Айырымның қателіктері. X=x ₁ -x ₂ , x ₁ >x ₂ >0 болсын және азайғыш пен азайтқыштың жуық мәндері мен абсолютті қателіктері белгілі болсын.

a) айырымның абсолютті қателігі: .

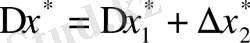b) айырымның салыстырмалы қателігі:

.

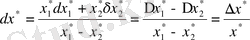3. Көбейтіндінің қателіктері. x=x ₁ *x ₂ *…*x _n көбейтіндісі берілсін. Көбейткіштердің жуық мәндері және абсолютті, салыстырмалы қателіктері белгілі болсын.

a) көбейтіндінің абсолютті қателігі:

.

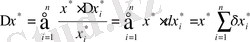b) көбейтіндінің салыстырмалы қателігі:

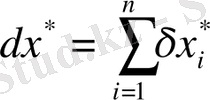
4 Бөліндінің қателігі: 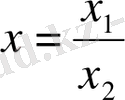бөліндісі берілсін. Алымы мен бөлімінің жуық мәндері, абсолютті, салыстырмалы қателіктері берілген болсын.

a) бөліндінің абсолютті қателігі: .

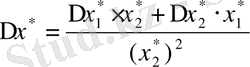b) бөліндінің салыстырмалы қателігі: .

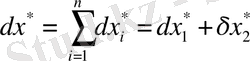Қарастырылатын сұрақтар (дәріс жоспары) :

1. Графиктік әдіс.

2. Жартылай қақ бөлу (дихотомия) әдісі.

Дәрістің қысқаша мазмұны:

Графиктік әдіс.

Айталық

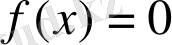(1)

теңдеуінің түбірлерін анықтау керек, мұнда 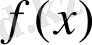- қандай да бір ақырлы немесе ақырсыз 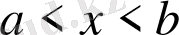аралығында анықталған және үзіліссіз функция.

Анықтама 1. 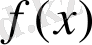фунқциясын нөлге айналдыратын, қандай да бір x мәні (1) теңдеудің түбірі деп аталады.

Анықтама 2. f(x) функциясының анықталу 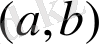облысына тиісті (1) теңдеудің тек бір ғана түбірі жататын аралықтарын анықтау теңдеудің түбірлерін жекешелеу деп аталады.

Анықтама 3. Түбірлерді жекешелеу кезінде анықталған аралықтағы теңдеудің түбірі үшін қабылданған бастапқы жуықтауды ε дәлдіктің дәрежесіне дейін жеткізуді түбірді дәлдеу деп атайды.

(1) теңдеудің тек бір түбірі жатқан кіші аралықты анықтау үшін математикалық талдау курсынан келесі теорема колданылады.

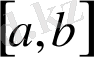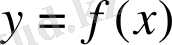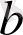Теорема. Егер аралығында анықталған, әрі үзіліссіз фунқциясы және нүктелерінде қарама-қарсы таңбалы мәндерді қабылдаса, яғни

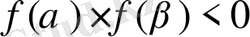(2)

теңсіздігі орындалса, онда осы аралықта (1) теңдеуінің кем дегенде бір түбірі болады.

Ал егер осындай 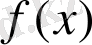функциясының туындысы бар болып және ол осы аралығында таңбасын өзгертпесе, онда 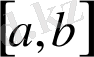аралығында (1) теңдеудің жалғыз түбірі болады.

(1) -ші теңдеудің нақты түбірлері 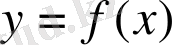қайсысының Ох осімен қиылысқан нүктелерінің абсциссалары болғандықтан түбірлерді жекешелеуді графиктік әдіспен анықтасақ болады.

Графиктік әдісінің алгоритмі:

1. (1) теңдеуді өзімен пара-пар теңдеумен алмастыруға болады

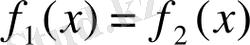
мұндағы - функциялары 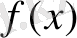функциясына қараған-да қарапайым фунқциялар болуы тиіс;

2) 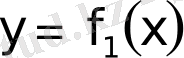және 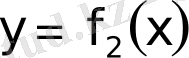функцияларының графиктерін саламыз;

3) осы графиктердің қиылысу нүктелерінің абсциссаларын анықтаймыз;

4) Егер табылған абсциссалар мәндері (2) теңсіздікті қанағаттандырса, онда осы графиктердің қиылысу нүктелерінің абсциссалары берілген теңдеудің ізделінді түбірлері болып табылады. Егер (2) теңсіздік орындалмаса, онда 3-ші пунктке ораламыз.

Жартылай қақ бөлу (дихотомия) әдісі.

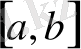(1) теңдеу берілсін. функциясы кесіндісінде үзіліссіз болсын және (2) теңсіздік орындалсын. 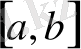кесіндіде жатқан (1) теңдеудің түбірін табу үшін осы кесіндіні қақ ортасынан бөлеміз.

Егер 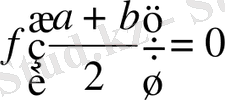болса, онда 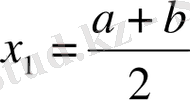берілген теңдеудің түбірі болып табылады, ал кері жағдайда, егер ,

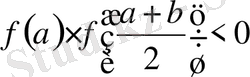онда 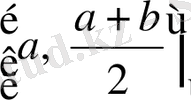кесіндіні қарастырамыз, әйтпесе 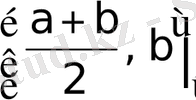кесіндіні қарастырамыз.

Әрі қарай , яғни 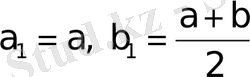немесе 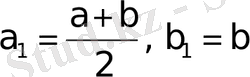кесіндісін тағы қақ бөлеміз. Нәтижесінде қандай да бір қадамда не (1) теңдеудің дәл түбірін аламыз, не бір бірінің ішінде орналасқан 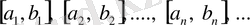шектеусіз тізбектерді аламыз.

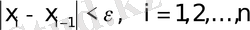(3)

жағдайда итерациялық процесті тоқтатамыз. Шешімнің қателік бағасының формуласы

.

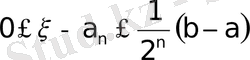Қарастырылатын сұрақтар (дәріс жоспары) :

1. Хорда әдісі.

2. Жанамалар (Ньютон) әдісі.

Дәрістің қысқаша мазмұны:

Хорда әдісі.

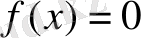теңдеуінің 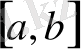аралығындағы берілген дәлдік-пен түбірін табу керек. Екі жағдай болуы мүмкін

1. , 2) .

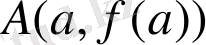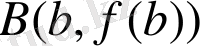Бірінші жағдайда және нүктелерінен өтетін хорда мен Ох осінің қиылысу нүктесін табу үшін 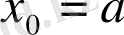болғанда келесі формуланы қолданамыз:

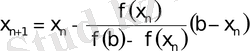(4)

Екінші жағдайда хорда әдісі үшін келесі негізгі формуланы аламыз

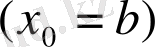
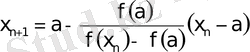(5)

Егер 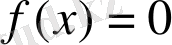теңдеуінің 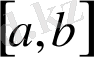-дағы дәл түбірін 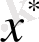деп, ал хорда әдісімен табылған түбірінің жуық мәнін ξ деп алсақ, онда осы жуык мәннің қателік бағасы

Итерация процесін

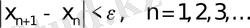
болғанда тоқтатамыз, мұнда ε>0 қандай да бір аз шама.

Жанамалар (Ньютон) әдісі.

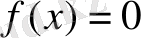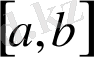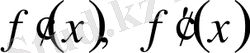
теңдеуінің ξ түбірі кесіндісінде жекеленген, үзіліссіз және анықталған таңбаны сақтайтын, сонымен қатар кесіндісінде үзіліссіз болсын. Ньютон әдісі у= f (x) қисығынын доғасын қисыктың қандайда бір нүктесінде жүргізілген жанамамен алмастырғанмен пара-пар.

Жанамалар (Ньютон) әдісінің негізгі формуласы:

(6)

Қателік бағасы

мұндағы х ^* - түбірдің дәл мәні;

ξ - түбірдің жуық мәні.

Қарастырылатын сұрақтар (дәріс жоспары) :

1. Гаусс әдісі.

2. Квадрат түбірлер әдісі.

Дәрістің қысқаша мазмұны:

Гаусс әдісі.

Гаусс әдісі белгісіздерді біртіндеп жою негізінде әртүрлі сұлба бойынша іске асырылуы мүмкін. Есептеу сұлбасын қандай да бір нақты мысалда қарастырған ыңғайлы. Сондықтан төртінші ретті теңдеулер жүйесін қарастырайық:

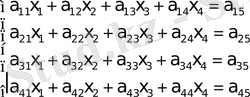(1)

( - бас элемент деп аталады) деп ұйғарайық. Гаусс әдісімен (1) сызықтық алгебралық теңдеулер жүйесін шешу процесі үшбұрышты теңдеулер жүйесін

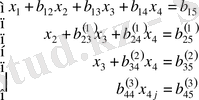(2)

құрумен пара-пар. Бас элементтің нөлден өзге болуы Гаусс әдісінің қолданылуының қажетті және жеткілікті шарты болып табылады.

Гаусс әдісінің тура жүрісі - коэффициенттерін табу

1. ,
2. , мұнда
3. , мұнда
4. .

Гаусс әдісінің кері жүрісі - белгісіздердің мәнін есептеу процесі.

Квадрат түбірлер әдісі.

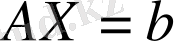сызықтық теңдеулер жүйесі берілсін, мұндағы А симметриялы матрица, яғни .

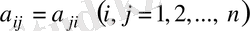Тура жүрісі. А матрицасын өзара транспонирленген екі үшбұрышты матрицаларының көбейтіндісі ретінде жазуға болады

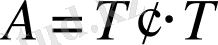, (1)

мұндағы

,

Т матрицасының 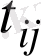элементтерін аныктау үшін 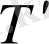және Т матрицаларын көбейтіп А матрицасына теңестіреміз.

(2)

(5) қатынас орындалса, (1) теңдеу келесі екі теңдеумен пара-пар

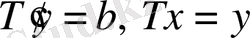. (3)

Кері жүрісі. (7) теңдеулерді жүйе арқылы жазамыз

және

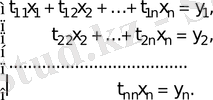
Осы жүйелерден біртіндеп у және х мәндерін табамыз:

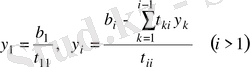
Қарастырылатын сұрақтар (дәріс жоспары) :

1. Жай итерациялық әдіс.
2. Зейдель әдісі.

Дәрістің қысқаша мазмұны:

Жай итерация әдісі.

Сызықтық теңдеулер жүйесінде белгісіздер саны көп болған жағдайда жүйенің түбірлерін табу үшін жуықталған сандық әдістерді қолданған ыңғайлы.

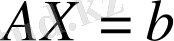(1)

сызықтық теңдеулер жүйесі берілсін және 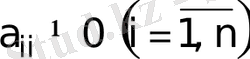деп үйғарайық Берілген (1) жүйені нормаль (келтірілген) жүйеге келтірейік

(2)

мұндағы

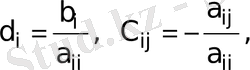егер ;

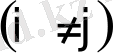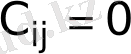, егер .

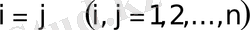Бастапқы жуықтау ретінде бос мүшелерді аламыз

.

Жалпы алғанда (2) жүйеден -ші жуықтау келесі формулалар арқылы табылады

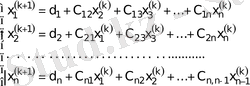(3)

Егер келесі шарттардың ең болмағанда біреуі орындалса

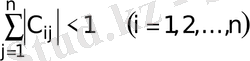(4)

немесе

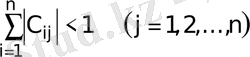. (5)

онда (3) итерация процесі бастапқы жуықтауды таңдауға тәуелсіз осы жүйенің жалғыз шешіміне жинақталады, яғни

.

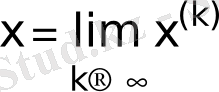Итерация процесін

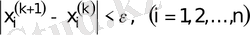(6)

болғанда тоқтатамыз, мұнда ε>0 қандайда бір аз шама.

Зейдель әдісі.

(2) -ші келтірілген сызықтық теңдеулер жүйесі берілсін. Түбірдің бастапқы жуықтауын еркін түрде таңдаймыз. Зейдель әдісі бойынша түбірдің +1 жуықтауын келесі формула бойынша есептейміз

Итерация әдісінде қарастырылған шарттар Зейдель әдісі үшін де тура. Зейдель әдісі итерация әдісіне қарағанда жақсы жинақталады .

Қарастырылатын сұрақтар (дәріс жоспары) :

1. А. Н. Крылов әдісі.

2. А. П. Данилевский әдісі.

Дәрістің қысқаша мазмұны:

А. Н. Крылов әдісі.

Кез келген 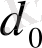бастапқы вектор берiлсiн, ал 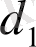мына формуламен анықталады:

Сонда (1) сипаттамалық теңдеуiнiң 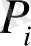коэффициентi мына жүйенi бередi

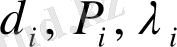-лердiң мәндерiн анықтағаннан кейiн меншiктiк векторы мына формуламен есептеледi

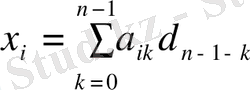
мұндағы

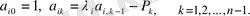
А. П. Данилевский әдісі.

Бұл әдiстiң мәндiлiгi n-1 түрлендiруiнен кейiн берiлген А матрицасы өсiне сәйкес Фробениус В матрицасына көшедi.

(1) сипаттамалық теңдеуiнде Р _k iзделiндi коэффициенттерi бар.

В матрицасының элементтерi мына формуламен есептеледi:

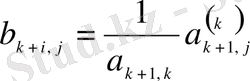
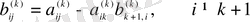
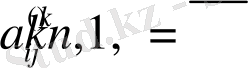
мұндағы 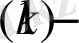- түрлендiру, сондықтан 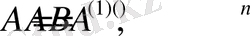. нөлге жақындағанда процесс туындауы мүмкiн. Меншiктiк вектор меншiктiк мәнiне сәйкес мына формуладан анықталады.

.

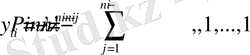
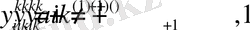
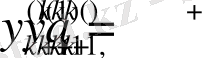Мұндағы

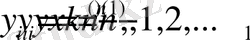
Қарастырылатын сұрақтар (дәріс жоспары) :

1. Функцияны жуықтау әдістері.
2. Тең емес арақашықтықта орналасқан түйiндерге арналған Лагранждың интерполяциялық формуласы.
3. Ньютонның интерполяциялық формулалары.

Дәрістің қысқаша мазмұны:

Функцияны интерполяциялау мәселесі.

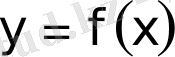функциясы берiлген және оның мәндерi кесте түрiнде берiлген. 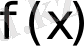- функциясы сияқты 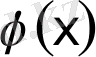- кез келген функциясы да 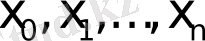нүктелерiнде дәл сондай мәндердi қабылдайды, ал берiлген аралықтағы өзге нүктелерде 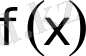функциясының қабылдайтын мәнiне, таңдалынған дәлдiкпен алғандағы, маңайлас шамаға тең.

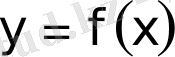функциясын берiлген тораптардан өзге нүктелерде 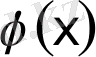функциясымен алмастырса, мұндай операцияны 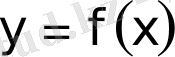функциясын интерполяциялау деймiз. Мұнда формуласы интерполяциялау формуласы деп аталады. Интерполяциялау формулалары 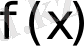функциясының аргументтiң берiлген мәндерi қарастырылған аралықта белгiсiз мәндерiн табу үшiн қолданылады.

Нәтижесiн шығарар кезде мынадай қателiктер ескерiледi:

1. Әдiс қателiгi.
2. Жойып алмау қателiгi.
3. Жуықтау қателiгi.

Әдiстiң қателiгi қалған мүшенi интерполяциялау формуласы арқылы табылуы мүмкiн және 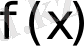- тiң сәйкес дәрежесiндегi туындысының интерполяциялау аралығындағы мәнiне байланысты бағаланады.

Тең емес арақашықтықта орналасқан түйiндерге арналған Лагранждың интерполяциялық формуласы

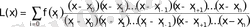(1)

Айталық, 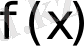функциясы аралығында тек 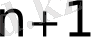-ге дейiнгi барлық дәрежеде туындысы табылады және қателiгi мына түрде болады.

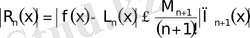(2)

,

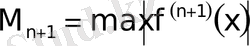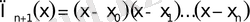
Тең емес арақашықтықта орналасқан түйiндерге арналған Ньютонның интерполяциялық формуласы

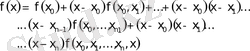(3)

(3) -тiң оң жағындағы барлық мүшелерiнiң қосындысы Ньютонның интерполяциялау көпмүшелiгi деп, ал соңғы мүшесi

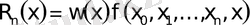(4)

қателiгi деп аталады.

Ньютонның бірінші интерполяциялау формуласы.

Тұрақты қадаммен берілген кесте, функцияға ақырлы түрлі кестесі құрылған. Интерполяциалау көп мүшелігін осындай түрде іздейміз:

(6)

Бұл n дәрежедегі көпмүшелік.

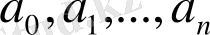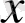коэфиценттерінің мағынасын, шыққан функцияның мағынасының сәйкестік шартын және көпмүшелік түйіндерін табамыз. -ге қарап, (5. 11) -ден -ді табамыз, одан . мәнді 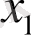және -ні бере отырып төмендегіні аламыз:

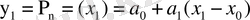, одан

тағы сол сияқты 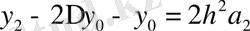, немесе

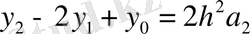
одан .

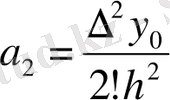
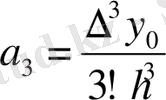Жалпы жағдайда үшін мынадай түр болады:

(7)

(6) -ші көпмүшелік үшін (7) -ні қоямыз:

(8)

Бұл формула басқаша түрде қолданылады

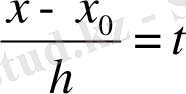болса, тағы сол сияқты

онда:

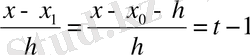
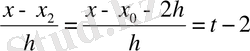
(9)

(9) - формула Ньютонның бірінші интерполяциондық формуласы деп аталады. Абсолюттік шамасы бойынша кіші болғанда, бұл формула интерполяцианың кесіндісінің басында интерполяциалау үшін қолданылады. Осы себепке байланысты Ньютонның бірінші интерполяциалау формуласын алға интерполяциалау деп атайды. Бастапқы 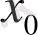мәнін 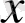аргументтегі кестелік мәнді қабылдауға болады.

Ньютонның екінші интерполяциялау формуласы.

Аргументтің мәні интерполяциалау кесіндісінің соңына жақын орналасқан кезде бірінші интерполяциалау формуласын қолдану тиімсіз. Бұл жағдайда артқа интерполяциалау, яғни, Ньютонның келесі түрде ізделінетін екінші интерполяциалау формуласы қолданылады:

(10)

Ньютонның бірінші формуласындағыдай 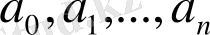коэффицентері түйінде функция мәндері және интерполяциалау көпмүшесінің сәйкес келу шартынан табылады.

(11)

(11) -шы өрнекті (10) -ші өрнекке қойып және 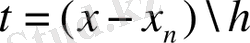айнымалысына өтіп, Ньютонның екінші формулаларының соңғы түрін аламыз:

(12)

Қарастырылатын сұрақтар (дәріс жоспары) :

1. Анықталған интегралдарды жуықтап есептеу әдістері.

2. Трапеция формуласы.

3. Симпсон формуласы.

4. Ньютон формуласы .

Дәрістің қысқаша мазмұны:

Келесідей анықталған интегралды есептегенде

,

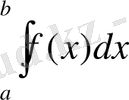мұндағы функциясы кесіндісінде үздіксіз, кейде белгілі Ньютон - Лейбниц формуласын қолдануға болады:

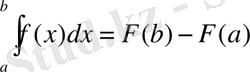(1)

мұндағы функциясының алғашқыбейнелерінің бірі болады (яғни, 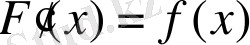) . Бірақ, сирек жағдайда, тәжірибе жүзінде алғашқыбейнені аналитикалық түрде алғанның өзінде, анықталған интегралдың сандық мәнін нақты соңына дейін есептей алмаймыз. Оған қоса, кейде интеграл астындағы функция таблица немесе график түрінде берілсе, онда интегралды не үшін (6. 18) формуласымен есептеу кең ауқымды практикалық қолданыс алмайтыны түсінікті болар еді.

Мұндай жағдайда жуықтап (сандық) интегралдаудың әртүрлі тәсілдері қолданылады.

Бір еселі интегралдарды жуықтап есептеуге қолданылатын формулалар квадратуралық формулалар деп аталынады. Квадратуралық формулаларды құрудың қарапайым әдісі мынадай болады. Интеграл астындағы функциясы кесіндісінде интерполяциялау көпмүшелігімен алмастырылады. Мысалы, 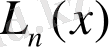-Лагранж көпмүшелігімен алмастырсақ, мынадай жуықтау теңдігі құрылады:

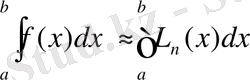, (2)

Мұндай әдіс ЭЕМ-де жеңіл орындалатын алгоритмдерге әкеліп, нәтижені нақты алу мүмкіндігін береді. Бұл жағдайда, кесіндісі бөлікке нүктелерімен бөлінеді, соның нәтижесінде 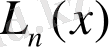көпмүшелігі құрылады.

Алынған нәтижені 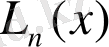көпмүшелігінің орнына қоя отырып, біз

,

мәнін аламыз.

Сонымен

, (3)

мұндағы

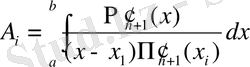, (4)

Осы табылған формулалар нәтижесін біле отырып, мынаны байқауға болады:

1) 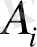коэффициенттері функциясына тәуелді еместігі, себебі олар интерполяциялау түйіндерін ескеріп құрылған.

2) Егер , -ші дәрежелі полином болса, онда (2) формуласы нақты болады, себебі, бұл жағдайда .

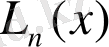
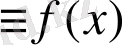Мұндағы x _к -интерполяцияның берiлген түйіндер, А _к -функцияның түрiне тәуелді емес тек түйіндер таңдауына тәуелдi коэффициенттер, R -қалдық мүше немесе квадратуралық формуланың қателiгi.

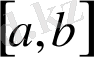интегралдау кесiндiсiн тең n бөлiкке бөлемiз:

интеграл астындағы функцияны алынған тораптарда есептеймiз.

Бiрдей қашықтықта жатқан тораптар үшiн квадратуралық формулалар Ньютон-Котес формулалары деп аталады. Бұндай формулалардың қарапайым түрлерi төменде келтiрiлген:

Трапеция формуласы.

(5)

мұндағы .

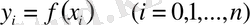Қалдық мүшесi келесi түрде есептелiнедi:

Симпсон формуласы.

,

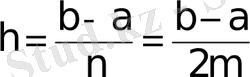(6)

Қалдық мүшесi келесi түрде есептелiнедi:

Ньютон формуласы.

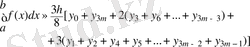(7)

мұндағы

.

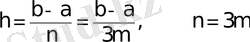№14

дәріс

Қарастырылатын сұрақтар (дәріс жоспары) :

1. Пикар әдісі.

2. Біртіндеп жуықтау әдісі.

3. Эйлер әдісі.

4. Рунге-кутт әдісі.

Дәрістің қысқаша мазмұны:

Пикар әдісі.

Бұл y ^/ =f(x, y) (1) диффенерциалды теңдеуді аналитикалық функция түрінде жақындатылған шешімін алуға мүмкіндік береді. Пикар әдісі (1) теңдеудің жалғыз шешімінің және табылу теоремасын дәлделдеуге байланысты пайда болады және мәні бойынша сығылған көріністің принципін қолданудың бірі болып табылады. Бастапқы (2) шарты бар (1) теңдеуінің шешімін табу теоремасының шартына сәйкес табу талап етілсін (1) теңдеуінің екі жағын x ₀ -ден x-ке дейін интегралдаймыз:

y(x ₀ ) =y ₀ (5)

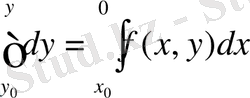
немесе

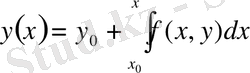(5)

(5) интегралды теңдеу шешімі дифференциалды теңдеуді және бастапқы шартты қанағаттандырады.

Шынында да, x=x ₀ кезінде аламыз:

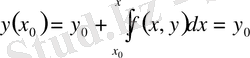
Сонымен (5) интегралдың теңдеудің шешімі тізбекті жақындау әдісін қолдануға мүмкіндік береді. y=y ₀ теңестіріп (5) теңдеуінен бірінші жақындауды аламыз:

Оң жақтағы интеграл тек x айнымалысынан тұрады, бұл интегралды тапқаннан кейін y ₁ (x) жақындаудың аналитикалық өрнегі x айнымалы функциясы сияқты алынады. Енді (5) теңдеуінде у-те табылған у ₁ (х) мәнімен алмастырамыз және екінші жақындауды аламыз;

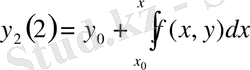
Және тағы сол сияқты.

Жалпы жағдайда интеграциялық формула мынадай түрде блады:

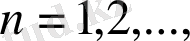(6)

(6) формуланың циклдық қолдануы төмендегі функция тізбегін береді:

Y ₁ (x), y ₂ (x), …, y _n (x) (7)

G-облысында f функциясы үзіліссіз болғандықтан, онда ол функция (х ₀ , у ₀ ) нүктесінен тұратын кейбір