Алгоритмдер және деректер құрылымдары: жылдам сұрыптау, AVL ағашын теңестіру және қызыл-қара ағашқа негізделген практикалық жұмыс


ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТІРЛІГІ
Л. Н. Гумилев атындағы Еуразия ұлттық университеті
Ақпараттық технологиялар факультеті
Компьютерлік және программалық инженерия кафедрасы
Алгоритмдер және деректер құрылымы пәні
К У Р С Т Ы Қ ЖҰ М Ы С
«6B06104 - Есептеу техникасы және бағдарламалық қамтамасыз ету» мамандығының
В057-6104-20-07 тобының студенті
Ермағамбетов Ержан Жандосұлы
тегі А. Ә.
Нұр - Сұлтан 2022
Мазмұны
Кіріспе
«Алгоритмдер және деректер құрылымы» пәнін оқу нәтижесінде программалау технологиясының жоғарғы деңгейі - динамикалық құрылымдарды қолдану алгоритмдері меңгерілді.
«Алгоритмдер және деректер құрылымы» пәнін меңгеру кезінде келесі динамикалық құрылымдардың әдістері мен қолдану жолдары қарастырылды:
- Бір және екі жақты байланысқан тізбектер;
- Стек және кезек динамикалық құрылымдары;
- Сұрыптау алгоритмдері;
- Екілік іздеу ағаштары (AVL ағашы, қызыл-қара ағаш, үйме ағашы) ;
- Екілік іздеу ағаштарын теңестірудің (оңға және солға, кіші және үлкен бұрулардың) алгоритмдері;
- Хэш функциялардың үлгілері;
- Хэш кестелерін құру және кестедегі қайшылықтарды шешу;
- Компьютер жадысында графты анықтаудың жолдары;
- Графтарды тереңінен және көлденеңінен қарастыру алгоритмдері.
1. Жылдам сұрыптау әдісі
Сұрыптау - күнделікті жұмыс және көп уақытты қажет етеді. Сұрыптау термині әдетте тізімдегі заттарды алдын-ала белгіленген тапсырыс қатынасы негізінде өсу немесе кему ретімен орналастыруды білдіреді. Сұрыптау көбінесе деректерді өңдеудегі тағы бір негізгі қызмет болып табылатын іздеуге арналған. Егер сөздіктерде сөздер ұйымдастырылмаған немесе сұрыпталмаған болса, сөздікті іздеу қаншалықты қиын болғанын елестетіп көріңіз. Бұл сөздіктегі жазбалардың стандартты алфавиттік тәртіпте сақталуының себебі. Көптеген тапсырмалар мен есептеулер жай сұрыптау арқылы оңай болмайды. Сұрыптау алгоритмдері суретке түсетін жерде.
Сұрыптау алгоритмі - тізімнің элементтерін белгілі бір тәртіпке, мысалы, ең төменнен жоғарыға, ең төменнен төменге, өсіп келе жатқан тәртіпке, азайту тәртібіне, алфавиттік т. с. с. ұйымдастыруға арналған әдіс. сандық және лексикографиялық тәртіпті құрайды. Алгоритмдер негізгі сұрыптау ретінде сұрыптауды жиі қолданады. Сұрыптау алгоритмдерінің алуан түрлері бар, олардың әрқайсысында көптеген әдістер қолданылады. Осындай танымал, бірақ қуатты алгоритмнің бірі - көп тармақты рекурсияға негізделген алгоритм болып табылатын Divide және Conquer алгоритмі. Жылдам сұрыптау және біріктіру сұрыптау - бөлу және жеңу алгоритміне негізделген екі жиі қолданылатын алгоритмдер.
Жылдам сұрыптау - бөлу және жеңу тәсіліне негізделген жоғары тиімді, бірақ тиімді сұрыптау алгоритмі, ол екі немесе одан да көп ішкі мәселелерге бөлініп, содан кейін рекурсивті түрде шешілетін динамикалық тәсілге өте ұқсас. Егер қосалқы есептердің мөлшері аз болса, онда олар еш қиындықсыз қарапайым түрде шешіледі. Жылдам сұрыптау алгоритмі бөлімді айырбастау сұрауы деп аталады, тізімді үш негізгі бөлікке бөледі: 1) жиынтық элемент (орталық элементтер), 2) айналмалы элементтерден аз элементтер және 3) айналмалыдан үлкен элементтер. Біліктің өзі екі топтың арасына өзінің соңғы орнына ауысады, содан кейін САҚТАНДЫҚ СОРТ рекурсивті қолданылады.
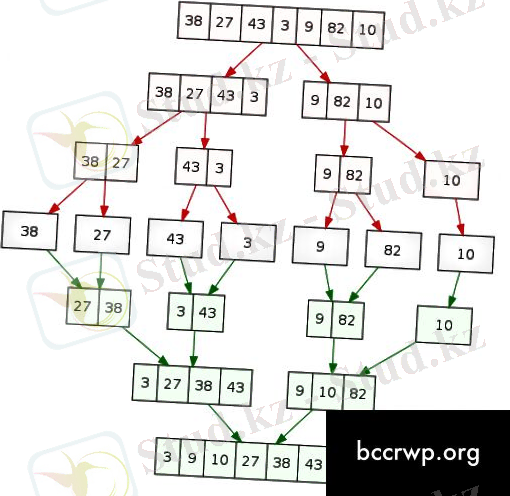
Жылдам сұрыптау және сұрыптауды біріктіру арасындағы айырмашылық
Жылдам сұрыптау және біріктіру сұрыптарының екеуі де бөлуге және жеңуге негізделген сұрыптау алгоритмдері бірдей негізгі қағидатқа ие - мәселені екі немесе одан да көп ішкі есептерге бөліп, содан кейін оларды рекурсивті түрде шешу. Алайда, олар біріктіру процедураларында және өнімділік жағынан ерекшеленеді. Жылдам сұрыптау әдетте басқа сұрыптау алгоритмдеріне қарағанда жақсы және жылдам, бұл кішігірім деректер жиынтығына кіру кезінде сұрыптауды қосады, ал сұрыптауды біріктіру деректер жиынтығының түріне қарамастан сәйкестікті сақтайды. Жылдам сұрыптау массивтер үшін өте жақсы, ал Біріктірілген сұрыпталған сілтемелер үшін өте жақсы.
Ғарыштық күрделілік Жылдам сұрыптау алгоритмінде сұрыптау рекурсивті түрде жасалады және әр рекурсивті қоңырау үшін стек орын қажет. Ол біріктіруге арналған қосымша орынды қажет етпейді, біріктіруге арналған бір жадтан басқа. Бұл орнында сұрыптау алгоритмі болғандықтан, сұрыптау үшін қосымша орын қажет емес. Шындығында, ол массивті бөлу және біріктіру кезінде бірдей жиымды қолданады. Merge Sort, екінші жағынан, деректерді файлда немесе массив түрінде ұсынудың бірнеше жолдары бар, сондықтан оған қосымша орын қажет ететін ішкі файлдар немесе масштабтағы өлшемдер сияқты жұмыс аумақтары қажет. Ең нашар істің күрделілігі Жылдам сұрыптау үшін ең нашар жағдай бөлу теңестірілмеген кезде пайда болады, ол бөлу үшін қандай элементтер қолданылатынына байланысты болады, алгоритм кірістіру сұрыпталуы сияқты асимптотикалық түрде баяу жұмыс істейді. Жылдам сұрыптаудың ең нашар көрсеткіші - O (n2) және жаттығу ретінде қалады. Дегенмен, дұрыс бұрылысты таңдау арқылы оны болдырмауға болады. Merge Sort-тің ең нашар жағдайы, керісінше, ең көп салыстыруды орындау қажет болған кезде пайда болады. Біріктірудің сызықтық өнімділігін ескерсек, сұрыптаудың ең нашар көрсеткіші O (n log2 n) болып табылады. Қысқаша мәліметЖылдам сұрыптау және біріктіру сұрыптау алгоритмдері де бөлуге және сұрыптауға арналған тәсілге негізделген. Дегенмен, олар бөлу және біріктіру процедураларын орындау үшін қолданылатын әдістермен ерекшеленеді. Олар негізінен бірдей принцип бойынша жұмыс істейді - мәселені екі немесе одан да көп ішкі проблемаларға бөліп, содан кейін оларды рекурсивті түрде шешу. Біріктіру сұрыптау нашар жағдайда жылдам сұрыптауға қарағанда тиімді, бірақ екеуі орташа жағдайда бірдей тиімді. Жылдам сұрыптау - Merge Sort сұрыптауынан гөрі кең орынды. Осылайша, Жылдам сұрыптау, біріктірудің сұрыптауынан гөрі тезірек және жақсырақ, бірақ салыстыруға келгенде кейбір жағдайларда тиімсіз болады.
2. AVL- ағашты байланыстыру. Солға үлкен бұру
 AVL ағашы
(Aдельсон-Velsky және Landis өнертапқыштардың атымен аталады ) - бұл өзін-өзі теңдестіретін екілік іздеу ағашы. Мұндай бірінші болды мәліметтер құрылымы ойлап табу керек. [2] AVL ағашында биіктіктер екеуінің бала кез-келген түйіннің ішкі ағаштары ең көбімен ерекшеленеді; егер кез-келген уақытта олар бірнешеден ерекшеленетін болса, қайта теңгерімдеу осы қасиетті қалпына келтіру үшін жасалады. Іздеу, енгізу және жою қажет O(журнал
n
) орташа және нашар жағдайдағы уақыт, қайда - бұл операцияға дейінгі ағаштағы түйіндердің саны. Енгізу және жою ағашты бір немесе бірнеше баланстың теңгерімдеуін талап етуі мүмкін ағаштардың айналуы. AVL ағашы екеуінің атымен аталған Кеңестік өнертапқыштар, Георгий Адельсон-Вельский және Evgenii Landis, оны 1962 ж. «Ақпаратты ұйымдастырудың алгоритмі» мақаласында жариялады. [3] AVL ағаштарын жиі салыстырады қызыл-қара ағаштар өйткені екеуі де бірдей операциялар жиынтығын қолдайды және қабылдайды негізгі операцияларға арналған уақыт. Іздеуді қажет ететін қосымшалар үшін AVL ағаштары қызыл-қара ағаштарға қарағанда жылдамырақ, өйткені олар қатаң теңдестірілген. [4] Қызыл-қара ағаштарға ұқсас, AVL ағаштары биіктікте теңдестірілген. Екеуі де жалпы емес салмақ теңдестірілген не - кез-келген үшін теңдестірілген ; [5] яғни, бауырластар түйіндерінің ұрпақтарының саны әр түрлі болуы мүмкін. AVL ағашына бірнеше элементтер кірістірілген анимация. Оған солға, оңға, солға-оңға және оңға-солға айналу кіреді.
AVL ағашы
(Aдельсон-Velsky және Landis өнертапқыштардың атымен аталады ) - бұл өзін-өзі теңдестіретін екілік іздеу ағашы. Мұндай бірінші болды мәліметтер құрылымы ойлап табу керек. [2] AVL ағашында биіктіктер екеуінің бала кез-келген түйіннің ішкі ағаштары ең көбімен ерекшеленеді; егер кез-келген уақытта олар бірнешеден ерекшеленетін болса, қайта теңгерімдеу осы қасиетті қалпына келтіру үшін жасалады. Іздеу, енгізу және жою қажет O(журнал
n
) орташа және нашар жағдайдағы уақыт, қайда - бұл операцияға дейінгі ағаштағы түйіндердің саны. Енгізу және жою ағашты бір немесе бірнеше баланстың теңгерімдеуін талап етуі мүмкін ағаштардың айналуы. AVL ағашы екеуінің атымен аталған Кеңестік өнертапқыштар, Георгий Адельсон-Вельский және Evgenii Landis, оны 1962 ж. «Ақпаратты ұйымдастырудың алгоритмі» мақаласында жариялады. [3] AVL ағаштарын жиі салыстырады қызыл-қара ағаштар өйткені екеуі де бірдей операциялар жиынтығын қолдайды және қабылдайды негізгі операцияларға арналған уақыт. Іздеуді қажет ететін қосымшалар үшін AVL ағаштары қызыл-қара ағаштарға қарағанда жылдамырақ, өйткені олар қатаң теңдестірілген. [4] Қызыл-қара ағаштарға ұқсас, AVL ағаштары биіктікте теңдестірілген. Екеуі де жалпы емес салмақ теңдестірілген не - кез-келген үшін теңдестірілген ; [5] яғни, бауырластар түйіндерінің ұрпақтарының саны әр түрлі болуы мүмкін. AVL ағашына бірнеше элементтер кірістірілген анимация. Оған солға, оңға, солға-оңға және оңға-солға айналу кіреді.
AVL ағашы - бұл теңдестірілген екілік іздеу ағашының түрі, онда әр ішкі түйіннің екі баласының биіктігі бір-біріне сәйкес келуі керек. Сыртқы түйіннің биіктігі нөлге тең, ал кез-келген ішкі түйіннің биіктігі әрқашан екі баласының биіктігінің максимумы болып табылады. Осылайша, AVL ағашының биіктік функциясы WAVL ағашының шектеулеріне бағынады және біз кез-келген AVL ағашын WAVL ағашына айналдырып, әр түйіннің биіктігін оның дәрежесі ретінде қолдана аламыз.
AVL ағашы мен WAVL ағашының арасындағы негізгі айырмашылық түйінде бірдей дәрежеге немесе бойға ие екі бала болған кезде пайда болады. AVL ағашында, егер түйін болса х бойымен бірдей екі баласы бар сағ ретінде, содан кейін биіктігі х дәл болуы керек сағ + 1. Керісінше, егер WAVL ағашында, егер түйін болса х бір деңгейдегі екі баласы бар р ретінде, содан кейін дәрежесі х болуы мүмкін р + 1 немесе р + 2. Себебі дәреже WAVL ағашындағы биіктікке қатаң тең келмейді. Бұл дәрежелердегі үлкен икемділік құрылымдардағы үлкен икемділікке әкеледі: кейбір WAVL ағаштарын олардың қатарларын өзгерту арқылы тіпті AVL ағаштары жасауға болмайды, өйткені олардың құрамына балалардың биіктігі бірден көп болатын түйіндер кіреді. Алайда, барлық AVL ағаштары WAVL ағаштары деп айта аламыз. AVL ағаштары дегеніміз - 2-дәреже айырмашылығының екеуі де бар түйіні жоқ WAVL ағаштары. Егер WAVL ағашы тек кірістіру операцияларын қолдану арқылы жасалса, онда оның құрылымы сол кірістіру ретімен құрылған AVL ағашының құрылымымен бірдей болады және оның қатарлары сәйкес AVL ағашының қатарларымен бірдей болады. Тек жою операциялары арқылы WAVL ағашы AVL ағашынан өзгеше бола алады. Атап айтқанда, бұл тек кірістіру арқылы жасалған WAVL ағашының биіктігі ең жоғары болатындығын білдіреді
Байланыстыру дегеніміз −сол және оң жақ ішкі ағаштардың биіктіктері h(L) -h(R) =2 айырмашылығы болған жағдайда, ағаштың қасиеті қалпына келтірілетін етіп, осы шыңның астындағы ата−баба ұрпағының байланысын өзгертетін операция. h(L) - H(R) ⩽1, әйтпесе ештеңе болмайды өзгертеді. Теңдестіру үшін біз әр шың үшін оның сол және оң жақ ішкі ағашының биіктігі арасындағы айырмашылықты сақтаймыз diff [i] = h (L) - h (R)
Кіші сол жақ бұрылыс:
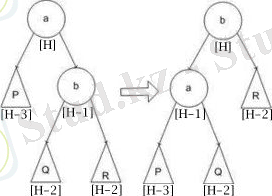
function rotateLeft(Node a) :
Node b = a. right
a. right = b. left
b. left = a
корректировка высоты a
корректировка высоты b
Үлкен сол жақ бұрылыс:
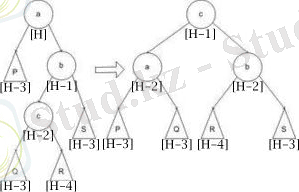
function big Rotate Left(Node a) :
rotateRight(a. right)
rotate Left(a)
3. Программалау есебі
Берілгені: Кездейсоқ жолмен алынған [0, 50] аралығындағы қайталанбайтын n бүтін саннан тұратын қызыл-қара ағашты құру керек. Қызыл-қара ағаштың суретін салу керек. Ағаштағы [ 15, 40] аралығындағы сандардың ең кішісін табу керек.
Коды:
#include <iostream>
using namespace std;
typedef enum {BLACK, RED} nodeColor;
struct rbNode
{
rbNode* left;
rbNode* right;
rbNode* parent;
nodeColor color;
int data;
};
#define NIL &nullbytak
rbNode nullbytak = { NIL, NIL, 0, BLACK, 0 };
rbNode* root = NIL;
void rotateLeft(rbNode* x)
{
rbNode* y = x->right;
x->right = y->left;
if (y->left != NIL)
y->left->parent = x;
if (y!=NIL)
y->parent = x->parent;
if (x->parent)
{
if (x == x->parent->left)
x->parent->left = y;
else x->parent->right = y;
}
else root = y;
y->left = x;
if (x != NIL)
x->parent = y;
}
void rotateRight(rbNode* x)
{
rbNode* y = x->left;
x->left = y->right;
if (y -> right != NIL)
y->right->parent = x;
if (y != NIL)
y->parent = x->parent;
if (x->parent)
{
if (x == x->parent->right)
x->parent->right = y;
else x->parent->left = y;
}
else root = y;
y->right = x;
if (x != NIL)
x->parent = y;
}
void insertFixup(rbNode* x)
{
while (x != root && x->parent->color == RED)
{
if (x->parent == x->parent->parent->left)
{
rbNode* y = x->parent->parent->right;
if (y->color == RED)
{
x->parent->color = BLACK;
y->color = BLACK;
x->parent->parent->color = RED;
x = x->parent->parent;
}
else
{
if (x == x->parent->right)
{
x = x->parent;
rotateLeft(x) ;
}
x->parent->color = BLACK;
x->parent->parent->color = RED;
rotateRight(x->parent->parent) ;
}
}
else
{
rbNode* y = x->parent->parent->left;
if (y->color == RED)
{
x->parent->color = BLACK;
y->color = BLACK;
x->parent->parent->color = RED;
x = x->parent->parent;
}
else
{
if (x == x->parent->left)
{
x = x->parent;
rotateRight(x) ;
}
x->parent->color = BLACK;
x->parent->parent->color = RED;
rotateLeft(x->parent->parent) ;
}
}
}
root->color = BLACK;
}
rbNode* insertrbNode(int data)
{
rbNode* current, * parent, * x;
current = root;
parent = 0;
while (current != NIL)
{
if (data == current->data) return(current) ;
parent = current;
current = (data < current->data) ? current->left:current->right;
}
x = (rbNode*) malloc(sizeof(rbNode) ) ;
x->data = data;
x->parent = parent;
x->left = NIL;
x->right = NIL;
x->color = RED;
if (parent)
{
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz