Айнымалысы модуль ішіндегі теңсіздіктер

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 53 бет
Таңдаулыға:

Қазақстан Республикасы Білім және ғылым Министрлігі А. Байтұрсынов атындағы Қостанай өңірлік университеті

Жанат Сұңқар

Орта мектепте модулі бар теңдеулер мен теңсіздіктерді шешуде оқытудың ерекшеліктері

Дипломдық жұмыс

5В010900 Математика

Қостанай 2021

Қазақстан Республикасы Білім және ғылым Министрлігі А. Байтұрсынов атындағы Қостанай өңірлік университеті

«Қорғауға жіберілсін»

Математика кафедрасы

Қолы Утемисова А. А.

«___» 2021ж.

ДИПЛОМДЫҚ ЖҰМЫС

Орта мектепте модулі бар теңдеулер мен теңсіздіктерді шешуде оқытудың ерекшеліктері

5В010900 Математика

Орындаған: Жанат Сұңқар

Оқу: күндізгі бөлімнің 4 курс студенті

Ғылыми жетекшісі: доцент Ысмагул Р. С

МАЗМҰНЫ

КІРІСПЕ . . .

КІРІСПЕ . . .: 1 Орта мектепте модульмен теңсіздіктерді шешуге дайындықты ұйымдастырудың теориялық-әдістемелік негіздері . . .

4: 7

КІРІСПЕ . . .: 1. 1 Модуль. Модульдің анықтамасы . . .

4: 7

КІРІСПЕ . . .: 1. 2 Санның модулі және модульдің негізгі қасиеттері . . .

4: 9

КІРІСПЕ . . .: 1. 3 Модуль таңбасымен берілген теңдеулер мен теңсіздіктер . . .

4: 14

КІРІСПЕ . . .: 1. 4 Мектеп математикасы курсында «Модульмен теңсіздіктерді шешу» тақы6рыбы бойынша оқу мақсаттары . . .

4: 16

КІРІСПЕ . . .: 1. 5 Негізгі мектеп бағдарламасындағы және мектептің математика оқулықтарындағы модуль таңбасымен берілген теңдеулер мен теңсіздіктерге есептер . . .

4: 19

КІРІСПЕ . . .: 1. 6 Негізгі алгебра курсында модульмен теңсіздіктерді шешуге үйрету бойынша әдістемелік ұсыныстар . . .

4: 22

КІРІСПЕ . . .: 1. 7 АКТ-ны қолдана отырып, модулі белгісіндегі айнымалысы бар теңдеулер мен теңсіздіктерді шешуге үйретудің әдістемелік ерекшеліктері . . .

4: 25

КІРІСПЕ . . .: 2 Практикалық бөлім . . .

4: 30

КІРІСПЕ . . .: 2. 1. 6-сыныпта модуль таңбасы бар теңдеулер мен теңсіздіктерге берілген есептерді шешуге нұсқаулық . . .

4: 30

КІРІСПЕ . . .: 2. 1. 1 Модулі бар теңдеулер мен теңсіздіктерді шешуге арналған кесте . . .

4: 30

КІРІСПЕ . . .: 2. 1. 2 Айнымалысы модуль ішіндегі теңдеулер . . .

4: 33

КІРІСПЕ . . .: 2. 1. 3 Айнымалысы модуль ішіндегі теңсіздіктер . . .

4: 36

КІРІСПЕ . . .: 2. 2. 6 «Б» сыныбына жүргізілген педагогикалық сараптама . . .

4: 37

КІРІСПЕ . . .: 2. 3 Сабақ әзірлемелері . . .

4: 46

КІРІСПЕ . . .: ҚОРЫТЫНДЫ . . .

4: 61

КІРІСПЕ . . .: ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . .

4: 62

КІРІСПЕ

Бұл дипломдық жұмыс оқушылардың білімін кеңейтуге, әртүрлі бағыттағы есептерді шешу арқылы математикалық дайындық деңгейін арттыруға бағытталған "модулі бар теңдеулер мен теңсіздіктер" тақырыбы бойынша элективті курс ретінде пайдаланылуы мүмкін. Айта кету керек, модулі бар теңдеулерді, теңсіздіктерді шешу және модулі бар қарапайым функциялардың графигін құру дағдылары негізгі мектеп курсы үшін пән бойынша емтиханды сәтті тапсырып қана қоймай, сонымен қатар 10-11 сыныптарда оқуға, емтихан тапсыруға және одан әрі жоғары оқу орындарына түсуге жақсы дайындалғысы келетін оқушыға қажет. Материалда модулі бар тапсырмалардың кең класын тиімді шешуге мүмкіндік беретін "стандартты емес" әдістер бар. Математиканы оқытудың негізгі міндеті - оқушылардың математикалық білім мен дағдылар жүйесін берік және саналы игеруін қамтамасыз етумен қатар, бұл жұмыс пәнге тұрақты қызығушылықты қалыптастыруды, математикалық қабілеттерді анықтауды және дамытуды, математикамен байланысты мамандықтарға бағдарлауды қамтиды.

Осы жұмыста ұсынылған тапсырмаларды шешу қызықты және оңайырақ, бұл оқушылардың оқу мотивациясын арттыруға және олардың математика қабілеттерін тексеруге мүмкіндік береді. Сонымен қатар, мазмұн кез-келген деңгейдегі оқушыға оқу-танымдық процеске белсенді қатысуға және өзін барынша көрсетуге мүмкіндік береді.

Оқушы әдемі шешілген тапсырмадан, математиканы басқа пәндерге қолдану мүмкіндігінен эстетикалық қанағаттануды сезінуі керек. Проблемалық оқытуды қолдану сабақтарды қызықты және тиімді етеді.

Бұл жұмыс оқушыларды модульдермен алгебралық есептерді шешудің аналитикалық және функционалды-графикалық әдістерімен таныстырады. Осы курсты зерделеу нәтижесінде өзін-өзі бағалау элементтерін жүзеге асыру, өзара бағалау, математикалық әдебиеттермен жұмыс істеу және ең бастысы жұптық, топтық іс-әрекет әдістері қолданылады.

Дипломдық жұмыстың өзектілігі: Математиканы оқыту барысында оқушылардың дайындықтарының тиімділігі мен білімдерінің сапасы дәстүрлі емес тұрпаттар, әдістер мен тәсілдер жүйесін құру арқылы жүзеге асырылуы мүмкін, сондықтан әдістемелік нұсқаулықтарды қолданып, модулі бар теңдеулер мен теңсіздіктерді шешу өзекті мәселелердің бірі болып табылады.

Абсолютті шама нақты және күрделі сандар саласында санның маңызды сипаттамаларының бірі болып табылады. Мектептегі математика курсының әртүрлі бөлімдерінде, сондай-ақ жоғары математика мен физиканы зерттеуде модуль ұғымы жиі қолданылады. Мысалы, жуық есептеулер теориясында шамамен санның абсолютті және салыстырмалы қателері туралы ұғымдар қолданылады. Математикалық анализде модуль ұғымы шекті, шектеулі функция және т. б. сияқты ең негізгі ұғымдардың анықтамаларында кездеседі. Механика мен геометрияда вектор және оның ұзындығы (вектор модулі) ұғымдары зерттеледі. Абсолютті мәндермен байланысты есептер математикалық олимпиадаларда, университеттерге түсу емтихандарында, ҰБТ да жиі кездеседі.

Математикадан негізгі жалпы білім беру бағдарламасында арифметика бөлімінде «рационал сандар» тақырыбында қысқаша жазылған: «санның модулі (абсолютті шамасы) ». Бұл ұғым аталған бағдарламада да, Орта (толық) білім беру бағдарламасында да айтылмайды. «Модуль» ұғымы алтыншы сыныптың математика курсына оның геометриялық мағынасы арқылы енгізіледі, бірақ сандар жиынындағы унитарлық операция ретінде емес. Әрі қарай, 6-сыныпта модуль сандарды салыстыру кезінде, оң және теріс сандарды көбейту және бөлу кезінде қолданылады, сонымен қатар модульді қолдана отырып бірнеше қарапайым теңдеулер мен теңсіздіктер келтірілген. [1]

Орта мектепте модульмен теңсіздіктерді зерттеу жағдайы апатқа жақын деп айта аламыз. Негізгі және орта мектепті бітіргеннен кейін студенттер математика пәнінен емтиханнан да өтуі керек, ал емтихан бөлімінің көптеген тапсырмаларында әртүрлі типтегі модульмен тапсырмалар бар, және бұрын-соңды ойластырылмаған осындай күрделі деңгейдегі тапсырмалар болады.

Қарастырылып отырған тақырыптың өзектілігі дәл осы мектептегі білімдегі алшақтықта жатыр, өйткені «модуль» тақырыбында қарапайым тапсырмадан қиынына өту іс жүзінде жоқ. Модуль кез-келген функцияны, кез-келген теңдеуді немесе теңсіздікті керемет түрде өзгертеді, оларды күрделі етіп қана қоймай, қызықты етеді.

Сонымен қатар, жоғары оқу орындарына түсу емтихандарында және жақында ҰБТ кезінде модульмен берілген тапсырмалар үнемі қатысады. Біреу мектеп оқушыларына оларды шешуге үйретуі керек және мұны мектеп математикасы сабақтарында тәрбиешілердің көмегіне жүгінбей-ақ жасауға болады.

Дипломдық жұмыстың мақсаты: Модулі бар теңдеулер мен теңсіздіктерді шешуді оқыту әдістемесін зерделеп, әдістемелік нұсқаулық құру және оны практикада қолданылуын құрастырып, сараптама жүргізу.

Дипломдық жұмыстың міндеттері:

Модулі бар теңдеулер мен теңсіздіктерді шешу әдістемесінің теориялық негіздерін зерделеу.
Орта мектеп бағдарламасындағы оқулықтарға талдау жүргізу.
6-сыныпта модулі бар теңдеулер мен теңсіздіктерді шешуді оқыту әдістемесі бойынша нұсқаулық дайындау.
Гипотезаны тексеруге бағытталған сараптаманы өткізу.

Зерттеу объектісі: Модулі бар теңдеулер мен теңсіздіктер.

Зерттеу пәні: 6 сынып оқушыларының модулі бар теңдеулер мен теңсіздіктерді шығару процесінде оқу қызметі.

Жаңашылдығы: Модулі бар теңдеудлер мен теңсіздіктерді шешу әдістемесінің теориялық негіздері жүйелі зерделеніп, әдістемелік нұсқаулық құрастыру арқылы практикалық бөлімнің құрылуы болып табылады.

Тәжірибелік маңызы: Дипломдық жұмыс педагогикалық институттардың және университеттердің математика мамандығын таңдаған студенттер үшін машықтанудан өткенде, факультатив сабақтарын өткізгенде әдістемелік жәрдемші болады.

Гипотеза: егер 6-шы сынып оқушылары модулі бар теңдеулер мен теңсіздіктерді шығарудың әдістемелік нұсқаулығын қолданса, онда олардың танымдылық белсенділіктері мен қызығушылықтары артады және оқу үлгерімі жоғарылайды.

Зерттеудің теориялық және әдістемелік базасы. Зерттеудің теориялық негізін ғылыми жұмыстар, қазіргі заманғы отандық және шетелдік мамандардың математика саласындағы іргелі және қолданбалы зерттеулерінің нәтижелері құрайды. Зерттеу жүйелік тәсілдемеге, логикалық және салыстырмалы талдау әдістеріне негізделген.

Зерттеудің ақпараттық базасы ретінде аудармаға шыққан отандық және шетелдік басылымдар, әртүрлі анықтамалық материалдар, зерттелетін мәселелер бойынша конференция материалдары алынды.

Зерттеудің практикалық маңыздылығы. Зерттеу нәтижелерін математика мұғалімдері балаларды орта мектепте теңсіздіктерді модульмен шешуге үйрету кезінде қолдана алады.

Зерттеу құрылымы. Жұмыс кіріспеден, екі бөлімнен, қорытындыдан, әдебиеттер тізімінен және қосымшадан тұрады.

1 Орта мектепте модульмен теңсіздіктерді шешуге дайындықты ұйымдастырудың теориялық-әдістемелік негіздері

Модуль. Модульдің анықтамасы

Модуль (лат. modulus - өлшем) . қандай да бір аса маңызды коэффициенттің немесе шаманың (мысалы, тістер модулі , серпімділік модулі , комплекс сандар модулі ) атауы; құрылыстағы және сәулет өнеріндегі шартты бірлік. Бұл терминді өз кезегінде белгілі ғалым Исаак Ньютонның шәкірті болған ағылшын математигі және философы Роджер Котес алғаш рет енгізді деп саналады. [2]

Басқа нұсқа бойынша, 1806 жылы «модуль» терминін француз математигі Джордж Аргонне енгізген.

Немістің ұлы физигі, өнертапқышы, математигі және философы Готфрид Лейбниц те модуль функциясын өзі белгілеген жұмыстарында және жұмыстарында қолданды.

Осыған қарамастан, модульдің абсолюттік мән ретінде жалпы қабылданған және қазіргі мәнін тек 1841 жылы көрнекті неміс математигі Карл Вейерштрасс берді. ХІХ ғасырдың басында ғалымдар Арган мен Коши бұл сандарды күрделі сандарға енгізді. Бүгінгі күні модульдің функциясы өте қарапайым есептелгендіктен, ол іс жүзінде барлық бағдарламалау тілдеріндегі стандартты функциялар тізіміне енгізілген.

«Көп» және «кем» ұғымдары заттарды санауға және әр түрлі шамаларды салыстыру қажеттілігіне байланысты пайда болды. Ежелгі гректер теңсіздік ұғымын б. з. д ІІІ ғасырда қолданған. Архимед айналдыра есептей отырып, «кез-келген шеңбердің периметрі диаметрдің жетіден бірінен кіші, бірақ оннан жетпіс біріншіден асатын артықпен диаметрдің үш еселенгеніне тең» екенін анықтады. Басқаша айтқанда, Архимед $\pi\$ санның шекараларын көрсетті: $\ 3\frac{10}{71} < \pi < 3\frac{1}{7}.$

Евклид өзінің әйгілі «Бастамалар» трактатында бірқатар теңсіздіктер келтіреді. Мысалы, ол екі оң санның геометриялық ортасы олардың арифметикалық ортасынан үлкен емес және олардың гармоникалық орташасынан кем болмайтындығын, яғни $\frac{2a \bullet b}{a + b} \leq \overline{a \bullet b} \leq \frac{a + b}{2}\$ теңсіздіктің ақиқат екендігін дәлелдейді. Рим Папасы Александрияның (III ғасыр) «математикалық жиналысында» егер $\frac{a}{b} > \frac{c}{d}(a, b, c, d)$ болса, онда $ad > bc\$ болатындығы көрсетілген.

Алайда, бұл пайымдаудың барлығы ауызша жүргізіліп, көп жағдайда геометриялық терминологияға негізделген. Қазіргі теңсіздік белгілері 17-18 ғасырларда ғана пайда болды. $< және\ > \$ белгілерді ағылшын математигі Т. Гарриот (1560-1621), ал $\leq және\ \geq \$ белгілерін француз математигі П. Бугер (1698-1758) енгізген.

Санның модулі және модульдің негізгі қасиетттері

Санның өлшем бірлігі - математикада осындай қызықты ұғым, көптеген адамдар оны түсінуге қиналады. Дегенмен, бұл апельсин сияқты қарапайым. Бірақ оны түсіну үшін алдымен оның неге және кімге қажет екенін анықтайық.

Қараңыз . . .

Жағдай бір.

Өмірде теріс сандардың практикалық мәні жоқ жағдайлар жиі кездеседі. Мысалы, біз «минус 70 километрді» көлікпен жүре алмаймыз (қай бағытта жүрсек те 70 шақырым жүреміз), «минус 5 кг апельсинді» сатып ала алмайтынымыз сияқты. Бұл мәндер әрқашан оң болуы керек. Осындай жағдайларды белгілеу үшін математиктер арнайы термин - модуль немесе абсолютті мән ойлап тапты.

Екінші жағдай. Екінші жағдайВторой случай

ситуация два

Не удалось загрузить все результаты.

Повторить

Повторная попытка…

Не удалось загрузить все результаты.

Повторить

Повторная попытка…

Сіз Lay's чипсиін пакетін сатып аласыз. Сіз Lay's чиптерінің пакетін сатып аласыз. Пакетте оның салмағы 100 грамм екені айтылған. Бірақ, егер сіз пакеттерді өлшей бастасаңыз, олардың салмағы 100 грамм болуы екіталай. Олардың кейбіреулері 101 грамм, ал кейбіреулері 99 грамм болады. Егер сізде салмақ аз болса, сіз «Lay's» компаниясымен сотқа жүгіне аласыз ба?

Жоқ.

Себебі «Lay's» төзімділікті орнатады және сөмкенің салмағы 100 грамм болады, 1 грамм береді немесе алады дейді. Бұл «плюс немесе минус» - бұл модуль.

Үшінші жағдай

Үшінші жағдай

Третий случай

жағдай үш

ситуация три

Не удалось загрузить все результаты.

Повторить

Повторная попытка…

Не удалось загрузить все результаты.

Повторить

Повторная попытка…

Өмірде 100% дәл құндылықтар мүлдем жоқ. Мұндай толеранттылық әрдайым бар. Жалақыда, мысалы: «Мен айына 250 мың рубль жұмыс істеуге келісемін, плюс немесе минус 20 мың!» 20 мың - бұл модуль. Жалпы алғанда, қарапайымдылық үшін модуль кез-келген бағытта тірек нүктесінен қашықтық екенін ұмытпаңыз.

. . .

Ал, сіз әлдеқашан барлығын дерлік біледі.

. . .

Не удалось загрузить все результаты.

Повторить

Повторная попытка…

Енді толығырақ . . .

Санның модулі дегеніміз не?В общем случае, для простоты, иметь в виду, что модуль является расстоянием от опорной точки в любом направлении.

Жалпы, қарапайымдылық үшін, модуль кез келген бағытта бастапқы нүктеге дейінгі қашықтық екенін есте сақтаңыз.

В общем, для простоты учтите, что модуль - это расстояние до начальной точки в любом направлении.

Не удалось загрузить все результаты.

Повторить

Повторная попытка…

Не удалось загрузить все результаты.

Повторить

Повторная попытка…

Бұл сіз екеніңізді елестетіп көріңіз.

1-сурет

Сіз бір орында тұрып, алға да артқа да қозғала аласыз делік. Шығу нүктесін 0 деп белгілейік.

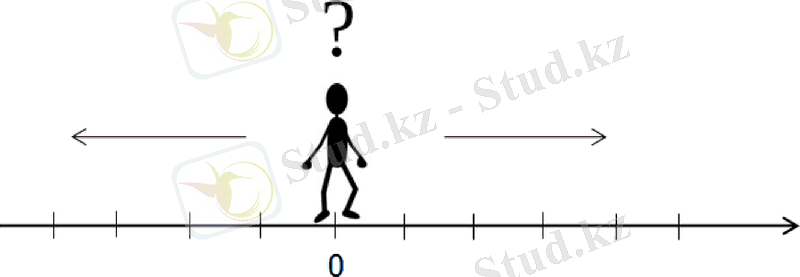
2-сурет

Сонымен, сіз 3 қадам алға басып, өзіңізді координатасы 3 болатын нүктеден табасыз.

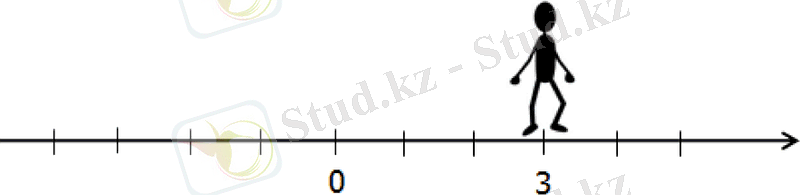
3-сурет

Бұл сіз 3 қадам (3 бірлік сегмент) тұрған жерден кеткеніңізді білдіреді. Яғни, қозғалыстың басынан бастап сіз аяқталған нүктеге дейінгі қашықтық 3-ке тең.

Бірақ сіз артқа қарай жүре аласыз!

Егер сіз 0 координатасы бар бастапқы нүктеден қарама-қарсы бағытта 3 қадам жасасаңыз, онда сіз -3 координатасы бар нүктеге жетесіз.

4-сурет

Бірінші және екінші жағдайда қандай қашықтық өтті?

Әрине, бірінші және екінші жағдайда өткен қашықтық бірдей және үшке тең болады, өйткені екі нүкте (3 және -3), онда сіз қозғалыс басталған нүктеден бірдей қашықтықта болдыңыз .

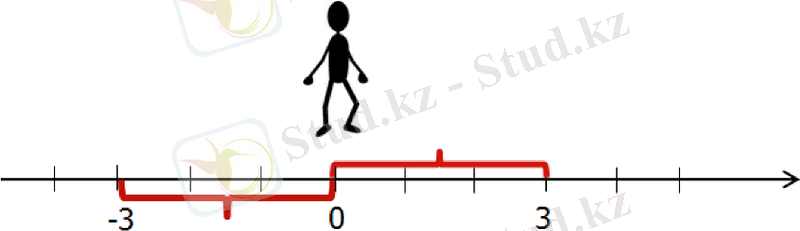
5-сурет

Осылайша біз модуль ұғымына жақындадық.

Модуль координаталық сегменттегі кез-келген нүктеден шығу нүктесіне дейінгі қашықтықты көрсетеді.

Сонымен, 5 санының модулі 5 болады. -5 санының модулі де 5-ке тең.

Себебі қашықтық теріс болмауы мүмкін! Модуль-абсолютті шама.

Модуль жай көрсетіледі:a, (a - кез келген Сан) .

Сонымен, 3 және -3 санының модулін табыңыз:

3=3

−3=3.

Анықтама 1. Санның модулі деп координаталық түзуде осы санды білдіретін нүктеден басталу нүктесіне дейінгі қашықтықты айтады.

Кейде «модуль» терминінің орнына санның «абсолютті мәні» термині қолданылады. Модуль $││\$ белгісімен көрсетілген.

Санның модулі мен санның арасында байланыс орнатып, анықтаманың аналитикалық жазбасын аламыз.

Анықтама 2.

$a = \left\{ \begin{array}{r} a, \ егер\ a \geq 0, \\ 0, \ егер\ a = 0, \\ - a, \ егер\ a < 0. \end{array} \right. \$

Санның модулін $a$ және $- a$ сандарының ең үлкені ретінде де анықтауға болады. Кейде модульдің анықтамасы арифметикалық квадрат түбір арқылы кездеседі.

Мысал 1. $x < 7\$ теңсіздігінің шешімдері $0 -$ ден басталып $7 -$ ге дейінгі барлық $x$ болып табылады. Олар $( - 7; 7)$ аралығында орналасқан.

Мысал 2. $x - 2 \leq 3$ теңсіздігінің шешімдері $2 -$ ден басталып $3 -$ тен аспайтын барлық $x$ болып табылады. Олар $\lbrack - 1; 5\rbrack$ аралығында орналасқан.

Мысал 3. $x > 4$ теңсіздігінің шешімдері $0 -$ ден басталып $4 -$ тен кем емес барлық $x$ болып табылады. Бұл екі бөлінбейтін сәулелердің бірігуі: (−∞; -4] ∪ [4; +∞) .

Мысал 4. $x + 3 > 5$ теңсіздігінің шешімдері $- 3 -$ тен басталып $5 -$ тен үлкен барлық $x$ болып табылады. Бұл екі қиылыспайтын сәулелердің кесілген бастаулармен үйлесуі: (−∞; -8) ∪ (2; +∞) .

Модульдің негізгі қасиеттері.

Барлық $x, y\epsilon R$ үшін:

a≥0, a \geq 0, \(Кез келген санның модулі-теріс емес сан)
−a=a - a = a, (Қарама-қарсы сандар модульдері тең)
a=a, a = a, \(Санның шамасы оның Модулінің шамасынан аспайды)
a•b=a•b, a \bullet b = a \bullet b, \(Екі санның көбейтіндісінің модулі, сол сандардың модульдерінің көбейтіндісіне тең)
ab=ab, (b≠0) \left \frac{a}{b} \right = \frac{a}{b}, \ (b \neq 0) (Бөлшектің модулі бөлгіштің модуліне бөлгіштің модулін бөлгенге тең (бөлгіш 0-ге тең болмаған жағдайда) )
an=an\left a^{n} \right = a^{n},
a2=a2\left a^{2} \right = a^{2}
a2k=a2ka^{2k} = a^{2k}\
a+b≤a+ba + b \leq a + b, (Қосындының модулі модулдердің қосындысынан аспайды)
a−b≤a±b≤a+b\left a - b \right \leq a \pm b \leq a + b\. Модуль таңбасымен берілген теңдеулер мен теңсіздіктер.

Нақты санның модулі (абсолют шамасы) деп $a \geq 0$ болғанда ол санның өзі, және $a < 0$ болғанда қарама-қарсы $a$ саны аталады. А санының модулі $a$ болып белгіленеді. Сонымен

$a = \left\{ \begin{array}{r} a, \ егер\ a \geq 0, \\ 0, \ егер\ a = 0, \\ - a, \ егер\ a < 0. \end{array} \right. \$

Мысалы: $\pi - 3 = \pi - 3, \$ өйткені $\pi - 3 > 0;$

$- 3, 7 = - ( - 3, 7) = 3, 7, \$ өйткені $- 3, 7 < 0.$

Геометриялық тұрғыдан $a$ координаталық түзуде $a\$ нүктесінің 0 нүктесінен қашықтығын білдіреді.

Мысалы: $- 3, 2$ дегеніміз $\ - \ 0$ нүктесінен сандар түзуін де белгіленген $( - 3, 2)$ нүктесіне дейінгі арақашықтығы.

Модульдің қасиеттері:

$a \geq 0; \ \ a = - a; \ ab = a \bullet b$ ,

$a^{2} = a^{2}$ ; $a \div b = a \div b, \ b \neq 0.$

$x - a = b\$ түріндегі теңдеуді геометриялық жолмен де шешуге болады.

1-мысал. $x - 5, 8$ = -3, 1 теңдеуін шешейік

$x - 5, 8$ = -3, 1 дегеніміз 0 нүктесінен $0, \ 2z + 2, 8\$ нүктесіне дейінгі арақашықтық $3, 1 -$ ге тең дегенді білдіреді. Ондай нүкте сандық осьте екеу: $- 3, 1$ және 3, 1.

Сондықтан келесі екі теңдеуді шешеміз:

$0, \ 2z + 2, 8\$ = 3, 1

$0, \ 2z + 2, 8\$ =-3, 1

Егер $0, \ 2z + 2, 8\$ = 3, 1 болса, онда $0, 2z = 0, 3; z = 1, 5\$

Егер $0, \ 2z + 2, 8\$ =-3, 1 болса, онда $0, 2z = - 5, 9; z = - 29, 5$

Жауабы: $z_{1} = 1, 5, \ \ z_{2} = - 29, 5$ .

2-мысал. $k - 3, 7 \leq 7$ теңсіздігін шешейік

Бұл теңсіздікті $- 7, 2 \leq k - 3, 7 \leq 7, 2\$ екі еселі теңсіздігі түрінде жазуға болады.

Теңсіздіктердің негізгі қасиеттерін ескеріп, теңсіздік мүшелеріне $3, 7$ санын қоссақ: $- 3, 5 \leq k \leq 10, 9\$ екі еселі теңсіздігін аламыз.

Жауабы: $k = \lbrack - 3, 5; 10, 9\rbrack$

Бұл есепті графиктік тәсілмен шешейік.

Егер $k - 3, 7 \geq 0$ болса, онда $k - 3, 7 = k - 3, 7$ және $k - 3, 7 \leq 7$ теңсіздігін шешу керек:

$\left\{ \begin{array}{r} k - 3, 7 \geq 0 \\ k - 3, 7 \leq 7 \end{array} \right. \ = > \left\{ \begin{array}{r} k \geq 3, 7, \\ k \leq 10, 9, \end{array} \right. \$

10, 9

3, 7

6-сурет

Демек, $( - 3, 5) -$ тен $10, 9$ аралығында жатқан $k -$ ның кез-келген мәні теңсіздікті қанағаттандырады.

Жауабы: $- 3, 5 \leq k \leq 10, 9.$

Мектеп математикасы курсында «Модульмен теңсіздіктерді шешу» тақырыбы бойынша оқу мақсаттары

Теңсіздіктер сызығы - математикадағы негізгі мағыналық жолдардың бірі. Теңсіздіктер сызығы функция ұғымына тікелей қатысты сұрақтарды зерттеу кезінде де, көптеген басқа ұғымдарда да жүзеге асырылады.

Негізгі жалпы білім берудің мемлекеттік білім беру стандартында «Математика» пәндік аймағын зерделеу нәтижелері мыналарды көрсетуі керек делінген:

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.