Тригонометриялық теңдеулерді, теңсіздіктерді және оның жүйелерін шешудің тиімді жолдары

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 12 бет
Таңдаулыға:

Қазақстан Республикасы Білім және Ғылым министрлігі Ақтөбе облыстық мамандандырылған физика-математикалық мектеп-интернаты

Баяндама
Тақырыбы:"Тригонометриялық теңдеулерді,теңсіздіктерді және оның жүйелерін шешудің тиімді жолдары"

Дайындаған:Таңатарова Ұ.Б

Ақтөбе 2022ж

Тақырып: Тригонометриялық теңдеулерді,теңсіздіктерді және оның жүйелерін шешудің тиімді жолдары
Мақсаты: Оқушылардың көп қиналатын тақырыптарының бірі- тригонометриялық теңдеулерді,теңсіздіктерді және оның жүйелерін тиімді шешудің жолдарын үйрету.
Міндеттері: Күнделікті әдебиеттерде кездесе бермейтін тригонометриялық теңдеулерді,теңсіздіктерді және оның жүйелерін шешудің ерекше жолдарын көрсете отырып, оқушылардың білім деңгейін арттыру,әрбір оқушыны жан-жақты білімді етіп тәрбиелеу.
Мектеп директоры: А.Жәлеке 21 11.2016
Тақырыбы:Классикалық би негізі
Мақсаты:Оқушылардың дене бітімін шынықтырып ,күшейте отырып классикалық би негізін қалаушыларды насихаттау.Өмірі мен шығармашылығымен,репетуарларымен таныстыру.

1.Кіріспе
Тригоннометрия-планиметрия мен стереометрияны кең қамтиды. 2. Негізгі бөлім
2.1 Тригонометриялық теңдеулерді шешу әдістері
2.2 Тригонометриялық теңсіздіктердің ерекшелігі
2.3 Тригонометриялық теңдеулер және теңсіздіктер жүйесі
3. Қорытынды 4. Пайдаланылған әдебиеттер

Кіріспе
Қай елдін болсын өсіп-өркендеуі, ғаламдық дүниеде өзіндік орын алуы оның ұлттық білім жүиесінің деңгейіне, даму бағытына байланысты. Білім - қоғамды әлеуметтік-мәдени, ғылыми үрдіспен қамтамасыз ететін жоғары құндылық. Болашақтың бүгінгіден нұрлы болуына ықпал етіп, адамзат қоғамы алға апаратын күш тек білімде ғана.
Жаңа ғасыр табалдырығын білім мен ғылымды инновациялық технология бағытымен дамыту мақсатымен аттауымыз үлкен үміттің басты нышаны болып табылады. Ұрпағы білімді халықтың болашағы бұлыңғыр болмайды дегендей, жас ұрпаққа сапалы, мән-мағыналы, өнегелі тәрбие мен білім беру - бүгінгі күннің басты талабы. Қазіргі кезеңде жалпы білімнің міндеті - баланың жалпылама дамуын қамтамасыз ету ғана емес, ең бастысы, оларды жастай өз қабілеті мен қызығуына қарай белгілі бір мамандыққа арнайы әзірлей білу.
Қазіргі заман - ғылым мен техниканың өркендеген, математика ғылымының өте жан - жақты тараған кезеңі. Ал, әрбір ұстаздың басты міндеті - жас ұрпаққа жан-жақты білім бере отырып, оқушының бойындағы қабілетін ашу арқылы, өмірге деген көзқарасын қалыптастыру. Математика пәніне қызығушылығын арттыру арқылы, логикалық ойлау қабілетін дамыту.
Тригонометрия ұғымдарымен мектеп оқушылары алғаш рет планиметрия курсында танысады. Кез келген жаңа ұғымға оқушы тарапынан: Бұл жаңалықты ең алғаш кім және не үшін ашты. Бізге ол қаншалықты қажет? деген сұрақ қойылуы заңды. Мұғалімді де жаңа тақырыпты оқыту қажеттілігі, дәлірек айтсақ, оқушының оқу қызметінің қажеттілігі, жаңа ұғымының қандай тәжірибелік негізде пайда болғандығы, тарихи даму кезеңдері, қазіргі кезде ғылым мен тәжірибеде алатын орны толғандырады. Оқушының өзін қызықтыратын объектіге талғап қарауынан сол объектінін (жаңа ұғымның) сырын ашуға деген тілек, талпыныс, қызығу, қажетсіну себептері туындайды Таңырқау - жаңалық ашудың анасы -деп физик Луи де Бройль тегін айтпаған Оқушыны бәрінен гөрі көп таңырқатып, оны проблемалық ситуацияға душар ететін нәрсе - ақпараттың жаңалығы, әдеттен тысқарылығы, кенеттілігі, оғаштығы, бұрынғы түсініктерге сәйкессіздігі, әсемдігі болып саналады. Тұтас алғанда бұлар танымдық қызығудың сезімдік - ойлау процестерін ширата түсетін аса күшті түрткілер болып табылады.
Бұл мақалада біз мұғалім сабақты қызықты өткізу үшін тригономтериялық теңдеулерді,теңсіздіктерді және оның жүйелерін бізге таныс емес жолмен шығаруға болатынына тоқталмақпыз

Негізгі бөлімі
Тригонометрия (грек. trіgōnon - үшбұрыш және metreo - өлшеу) - геометрияның үшбұрыш элементтерінің арасындағы метрикалық қатыс тригонометриялық функциялар арқылы өрнектелетін саласы. Тригонометрияның негізгі мәселесі үшбұрыштың белгісіз шамаларын берілген шамалар арқылы есептеу болып табылады. Тригонометрия жазық, түзу сызықты және сфералық тригонометрия болып бөлінеді.
Бастапқы кезден тригонометриялық функциялар тік бұрышты үшбұрыштағы қабырғаларының қатынастарымен байланыста болғаны белгілі. Олардың жалғыз аргументі сол үшбұрыштың бір сүйір бұрышы болып табылады.
Синус -- қарама-қарсы жатқан катеттің гипотенузаға қатынасы.
Косинус -- жанама катеттің гипотенузаға қатынасы.
Тангенс -- қарама-қарсы жатқан катеттің жанама катетке қатынасы.
Котангенс -- жанама катеттің қарама-қарсы жатқан катетке қатынасы.
Берілген анықтамалар функциялардың сүйір бұрыштарға (0-ден \pi \over 2 радиан) қатысты мендерін есептеуге арналған.
Тригонометриялық теңдеулерді шешудің әдіс тәсілдері. Тригонометриялық теңдеулерді шешу екі кезеңнен тұрады: теңдеуді қарапайым тригонометриялық теңдеуге түрлендіру және алынған қарапайым тригонометриялық теңдеуді шешу. Тригонометриялық теңдеулерді шешудің бірнеше әдіс- тәсілдері бар:
1. Алгебралық тәсіл.
2. Көбейткіштерге жіктеу тәсілі.
3. Біртекті теңдеуге келтіру.
4. Көмекші бұрыш енгізу әдісі.
5. Көбейтіндіні қосындыға түрлендіру.
6. Универсал алмастыру.
1) Теңдеуді шешіңіз: cos [2] x + sin x · cos x = 1.
Шешуі. cos [2] x + sin x · cos x - sin [2] x - cos [2] x = 0 ,
sin x · cos x - sin [2] x = 0 ,
sin x · ( cos x - sin x ) = 0 ,

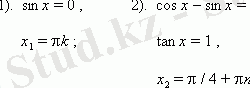
2) Теңдеуді шешіңіз: cos 2x - cos 8x + cos 6x = 1.
Шешуі. cos 2x + cos 6x = 1 + cos 8x ,
2 cos 4x cos 2x = 2 cos ² 4x
cos 4x · ( cos 2x - cos 4x ) = 0 ,
cos 4x · 2 sin 3x · sin x = 0 ,
1). cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,

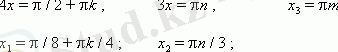
Жауабы:

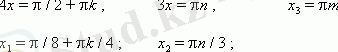
3) Теңдеуді шешіңіз: 3sin [2] x + 4 sin x · cos x + 5 cos [2 ]x = 2.
Шешуі. 3sin [2] x + 4 sin x · cos x + 5 cos [2] x = 2sin [2] x + 2cos [2] x ,
sin [2] x + 4 sin x · cos x + 3 cos [2] x = 0 ,
tg [2] x + 4 tg x + 3 = 0 ,
бұдан y [2] + 4y +3 = 0 .
Бұл теңдеудің шешімдері: y1 = -1, y2 = -3, бұдан
1) tg x = - 1, 2) tg x = - 3,

Анықтама. Тригонометриялық теңдеуі бар жүйені тригонометриялық теңдеулер жүйесі деп аталады.
Әр түрлі тригонометриялық теңдеулерді шешу алгебралық теңдеулерді шешу әдістеріне негізделіп шешіледі.

Теңдеулер жүйесін шешу әдістері

Алгебралық қосу ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.