Тригонометриялық теңдеулер мен теңсіздіктерді шешуде функцияның шенелгендік қасиетін қолдану


ТРИГОНОМЕТРИЯЛЫҚ ТЕҢДЕУЛЕР МЕН ТЕҢСІЗДІКТЕР ШЕШУДЕ ФУНКЦИЯНЫҢ ШЕНЕЛГЕНДІК ҚАСИЕТІН ҚОЛДАНУ
Есалина А. П.
Қ. Жұбанов атындағы Ақтөбе өңірлік университеті
Егер
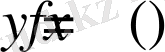 функциясы
Х
жиынында жоғарыдан да, төменнен де шенелген, яғни оң
С
саны табылып,
функциясы
Х
жиынында жоғарыдан да, төменнен де шенелген, яғни оң
С
саны табылып,
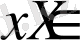 үшін
үшін
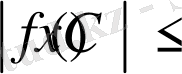 теңсіздігі орындалатын болса, онда
теңсіздігі орындалатын болса, онда
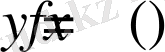 X
жиынында
шенелген функция
деп аталады. Басқаша айтқанда, функцияның
Х
жиынында шенелгендігі
X
жиынында
шенелген функция
деп аталады. Басқаша айтқанда, функцияның
Х
жиынында шенелгендігі
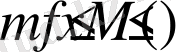 теңсіздігі барлық
теңсіздігі барлық
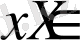 үшін орындалатындай
m
және
M
сандарының табылатындығын білдіреді.
үшін орындалатындай
m
және
M
сандарының табылатындығын білдіреді.
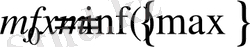 санын
санын
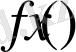 функциясының
дәл төменгі шекарасы
деп, ал
функциясының
дәл төменгі шекарасы
деп, ал
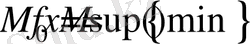 санын
санын
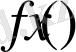 функциясының
дәл жоғарғы шекарасы
деп атайды.
функциясының
дәл жоғарғы шекарасы
деп атайды.
 айырмасы функцияның
Х
жиынындағы
тербелісі
деп аталады.
айырмасы функцияның
Х
жиынындағы
тербелісі
деп аталады.
Егер
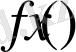 және
және
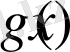 функциялары
Х
жиынында анықталған және шенелген болса, онда
функциялары
Х
жиынында анықталған және шенелген болса, онда
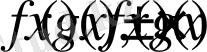 және
және
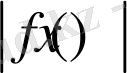 функцияларыда осы жиында шенелген болатын.
функцияларыда осы жиында шенелген болатын.
Тригонометриялық теңдеулер мен теңсіздіктерді шығаруда келесі тригонометриялық функциялардың шенелгендігін қолданамыз:
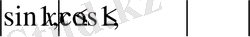
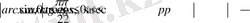
Есептерді шешудің мысалдары
Мысал 1.
 үшін функцияның ең кіші мәнін табыңыз:
үшін функцияның ең кіші мәнін табыңыз:
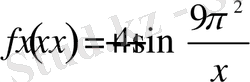
Шешуі: Өзара кері екі санның қосындысының қасиетін ескерсек:
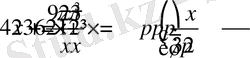
мұнда теңдік
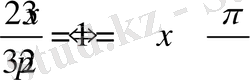 орындалады. Демек,
орындалады. Демек,
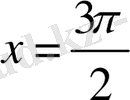 болғанда,
болғанда,
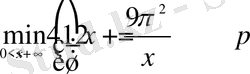
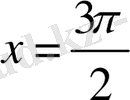 болғанда
болғанда
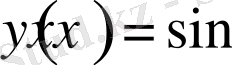 функциясы да ең кіші мәніне ие болады, яғни - 1, онда
функциясы да ең кіші мәніне ие болады, яғни - 1, онда
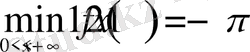
Жауабы:
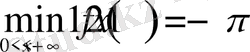
Мысал 2. Теңдеуді шешіңіз:
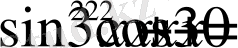
Шешуі: Қосылғыштарды топтастырып
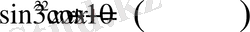
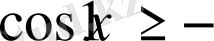 болғандықтан, онда теңдеудің сол жақ бөлігінде екі теріс емес өрнектердің қосындысы тұр. Ол нөлге тең болуы үшін әрбір қосылғыш жеке-жеке нөлге болуы қажет:
болғандықтан, онда теңдеудің сол жақ бөлігінде екі теріс емес өрнектердің қосындысы тұр. Ол нөлге тең болуы үшін әрбір қосылғыш жеке-жеке нөлге болуы қажет:
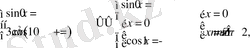
Мысал 3. q параметрінің қандай мәнінде теңдеулер жүйесінің шешімі бар болады?
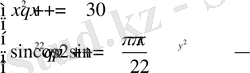
Шешуі: Екінші теңдеудің сол жақ бөлігі 1-ден кем емес, ал оң бөлігі 1-ден артық емес, демек, теңдеуле жүйесі келесі жүйеге эквивалентті:

Бірінші және соңғы теңдеуден келесіні аламыз:

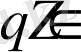 болғандықтан, бөлшектің бөлімі келесі төрт мәннің біріне тең болады:
болғандықтан, бөлшектің бөлімі келесі төрт мәннің біріне тең болады:
- Бұл жағдайда,
- болғандықтан, жарамайды.
- Бұл жағдайда,
Мысал 4.
Кез-келген
 үшін келесі теңсіздікті дәлелдеңіз:
үшін келесі теңсіздікті дәлелдеңіз:
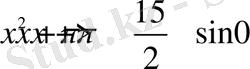
Шешуі
.
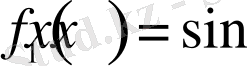 функциясының шенелгендігін ескерсек, келесі бағалау орындалады:
функциясының шенелгендігін ескерсек, келесі бағалау орындалады:
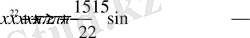
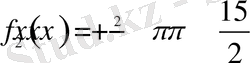 қарастырайық. Бұл квадрат үшмүшенің түбірлері
қарастырайық. Бұл квадрат үшмүшенің түбірлері
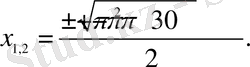
Демек,
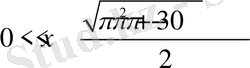 үшін
үшін
 ал
ал
 үшін
үшін

1)
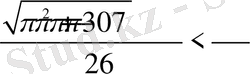 екенін байқайтын болсақ, бұл теңсіздік
екенін байқайтын болсақ, бұл теңсіздік
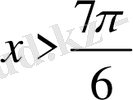 үшін орындалады. Ал
х
-тің қалған мәндері үшін екі жағдайды қарастырамыз.
үшін орындалады. Ал
х
-тің қалған мәндері үшін екі жағдайды қарастырамыз.
2)
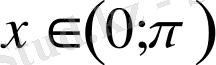 үшін теңсіздіктің сол жақ бөлігінде екі оң мән қабылдайтын функциялардың қосындысы орналасқан, яғни,
үшін теңсіздіктің сол жақ бөлігінде екі оң мән қабылдайтын функциялардың қосындысы орналасқан, яғни,
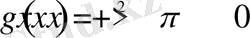 және
және
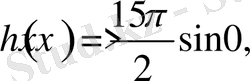 демек қарастырылып отырған аралықта теңсіздік орындалады.
демек қарастырылып отырған аралықта теңсіздік орындалады.
3)
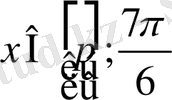 болсын
.
болсын
.
 және
және
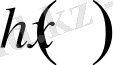 функцияларын төменнен бағалайтын болсақ
функцияларын төменнен бағалайтын болсақ
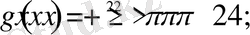
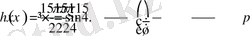
Демек, қосынды үшін келесі бағалау орынды
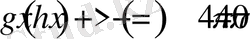
Барлық жағдайларды біріктіретін болсақ,
 үшін теңсіздіктің орындалатынына көз жеткіземіз.
үшін теңсіздіктің орындалатынына көз жеткіземіз.
Қолданылған әдебиеттер:
1. Пайдаланылған әдебиеттер тізімі:
1. Супрун В. П. Математика для старшеклассников. Нестандартые методы
2. Дыбов П. Т., Осколков В. А. Задачи по математике
3. Сборник задач по математике для поступающих во втузы. Под ред. Сканави М. И. 6-е изд. - М. : 2013
4. Бейсеков Ж., Онланова А. «Математикалық олимпиадаға даярлау» Шымкент 2012
Ғылыми жетекшісі - ф. ғ. к., доцент Иманчиев А. Е.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz