11-СЫНЫП ОҚУШЫЛАРЫНА АРНАЛҒАН ФУНКЦИЯНЫҢ ҚАСИЕТТЕРІН ПАЙДАЛАНЫП, ТЕҢДЕУЛЕР МЕН ТЕҢСІЗДІКТЕРДІ ШЕШУ ЭЛЕКТИВТІ КУРСЫН ӘДІСТЕМЕЛІК ҚАМТАМАСЫЗ ЕТУ

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

Қ. ЖҰБАНОВ атындағы АҚТӨБЕ ӨҢІРЛІК

УНИВЕРСИТЕТІ

Есалина Айзада Піралықызы

МАГИСТРЛІК ДИССЕРТАЦИЯ

11-СЫНЫП ОҚУШЫЛАРЫНА АРНАЛҒАН «ФУНКЦИЯНЫҢ ҚАСИЕТТЕРІН ПАЙДАЛАНЫП, ТЕҢДЕУЛЕР МЕН ТЕҢСІЗДІКТЕРДІ ШЕШУ» ЭЛЕКТИВТІ КУРСЫН ӘДІСТЕМЕЛІК ҚАМТАМАСЫЗ ЕТУ

7М01501 - Математика мамандығы

Ақтөбе

2021

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

Қ. ЖҰБАНОВ атындағы АҚТӨБЕ ӨҢІРЛІК

УНИВЕРСИТЕТІ

Математика кафедрасы

МАГИСТРЛІК ДИССЕРТАЦИЯ

11-СЫНЫП ОҚУШЫЛАРЫНА АРНАЛҒАН «ФУНКЦИЯНЫҢ ҚАСИЕТТЕРІН ПАЙДАЛАНЫП, ТЕҢДЕУЛЕР МЕН ТЕҢСІЗДІКТЕРДІ ШЕШУ» ЭЛЕКТИВТІ КУРСЫН ӘДІСТЕМЕЛІК ҚАМТАМАСЫЗ ЕТУ

Орындаушы:

7М01501-«Математика» мамандығының

2-курс магистранты Есалина А. П.

Ғылыми жетекшісі:

ф. -м. ғ., кандидаты, профессор Иманчиев А. Е.

Қорғауға жіберілді

Кафедра меңгерушісі,

ф. -м. ғ. к., доцент Тлеубергенова М. А.

«» 2021 ж.

Ақтөбе

2021

МАЗМҰНЫ

КІРІСПЕ

1. ЭЛЕКТИВТІ КУРСТЫҢ ҚҰРЫЛЫМЫ, МАҚСАТЫ МЕН МІНДЕТТЕРІ

НЕГІЗГІ БӨЛІМ

2. «ФУНКЦИЯНЫҢ ҚАСИЕТТЕРІН ПАЙДАЛАНЫП, ТЕҢДЕУЛЕР МЕН ТЕҢСІЗДІКТЕРДІ ШЕШУ» ЭЛЕКТИВТІ КУРСЫНЫҢ МАЗМҰНДЫҚ ҚҰРЫЛЫМЫ

2. 1 Функциялардың шенелгендік қасиетін пайдаланып, рационал және иррационал теңдеулер мен теңсіздіктерді шешу

2. 2 Функциялардың шенелгендік қасиетін пайдаланып, тригонометриялық теңдеулер мен теңсіздіктерді шешу

2. 3 Функциялардың шенелгендік қасиетін пайдаланып, көрсеткіштік теңдеулер мен теңсіздіктерді шешу

2. 4 Функциялардың шенелгендік қасиетін пайдаланып, логарифмдік теңдеулер мен теңсіздіктерді шешу

2. 5 Косинус және синус функцияларының шектеулілік қасиеттерін пайдаланып, теңдеулер мен теңсіздіктер шешу

2. 6 Кемімелі және өспелі функциялардың қасиеттерін пайдаланып теңдеулер мен теңсіздіктер шешу

2. 7 Функцияның монотондылық қасиетін пайдаланып, логарифмдік теңдеулер мен теңсіздіктерді шешу

2. 8 Функцияның монотондылық қасиетін пайдаланып, көрсеткіштік теңдеулер мен теңсіздіктерді шешу

3. «ФУНКЦИЯНЫҢ ҚАСИЕТТЕРІН ПАЙДАЛАНЫП, ТЕҢДЕУЛЕР МЕН ТЕҢСІЗДІКТЕРДІ ШЕШУ» ЭЛЕКТИВТІ КУРСЫНЫҢ ЭЛЕМЕНТТЕРІН МАТЕМАТИКА САБАҚТАРЫНДА ҚОЛДАНУДЫҢ ТИІМДІЛІГІ

ҚОРЫТЫНДЫ

2. «ФУНКЦИЯНЫҢ ҚАСИЕТТЕРІН ПАЙДАЛАНЫП, ТЕҢДЕУЛЕР МЕН ТЕҢСІЗДІКТЕРДІ ШЕШУ» ЭЛЕКТИВТІ КУРСЫНЫҢ МАЗМҰНДЫҚ ҚҰРЫЛЫМЫ

2. 1 Функциялардың шенелгендік қасиетін пайдаланып, рационал және иррационал теңдеулер мен теңсіздіктерді шешу

2. 1. ФУНКЦИЯ ШЕНЕЛГЕНДІГІН ТЕҢДЕУЛЕР ШЕШУДЕ ҚОЛДАНУ

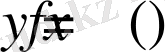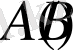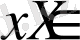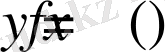функциясы Х жиынында анықталған болсын. Егер саны табылып, үшін теңсіздігі орындалса, онда функциясы Х жиынында төменнен (жоғарыдан) шенелген деп аталады. 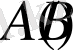санын функцияның төменгі (жоғарғы) шекарасы деп атайды. Функцияның төменнен (жоғарыдан) шенелгендігін дәлелдеу үшін оның ең болмағанда бір төменгі (жоғарғы) шекарасын көрсету жеткілікті.

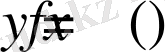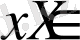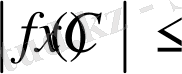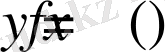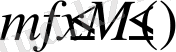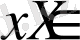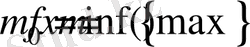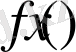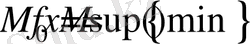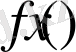Егер функциясы Х жиынында жоғарыдан да, төменнен де шенелген, яғни оң С саны табылып, үшін теңсіздігі орындалатын болса, онда X жиынында шенелген функция деп аталады. Басқаша айтқанда, функцияның Х жиынында шенелгендігі теңсіздігі барлық үшін орындалатындай m және M сандарының табылатындығын білдіреді. санын функциясының дәл төменгі шекарасы деп, ал санын функциясының дәл жоғарғы шекарасы деп атайды. айырмасы функцияның Х жиынындағы тербелісі деп аталады.

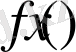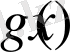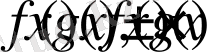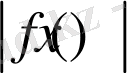Егер және функциялары Х жиынында анықталған және шенелген болса, онда және функцияларыда осы жиында шенелген болатын.

2. 2. БАҒАЛАУ ӘДІСІ. РАЦИОНАЛ ЖӘНЕ ИРРАЦИОНАЛ ТЕҢДЕУЛЕР МЕН ТЕҢСІЗДІКТЕР

Есептерді шешуде қолданылатын стандартты емес әдістердің бірі - бағалау әдісі. Бұл әдіс теңдеулермен теңсіздіктердегі функциялардың шенелгендігін пайдалануға арналған. Яғни, функциялардың ең үлкен және ең кіші мәндері арқылы функцияларды жоғарыдан және төменнен шенелгендігін есептер шешуде қолдануға бағытталады.

Анықтама 1. 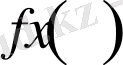функциясы D жиынында жоғарыдан шенелген деп аталады, егер , .

Анықтама 2. 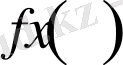функциясы D жиынында төменнен шенелген деп аталады, егер , .

Анықтама 3. 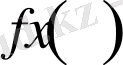функциясы D жиынында шенелген деп аталады, егер , .

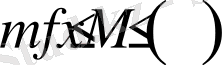Анықтама 3a. 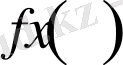функциясы D жиынында шенелген деп аталады, егер

, . (Бұл анықтама 3-анықтамаға эквивалентті)

Келесі фактілерді білген жөн:

• Егерболса, онда, теңдікорындалады.
• Егерболса, онда, теңдікорындалады.
• Егерболса, онда, теңдікорындалады.
• квадраттық функциясымәнімен, болғанда төменнен шенеледі, болғанда жоғарыдан шенеледі.
• Егержәнеболса, онда

.

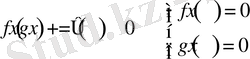• Егержәнеболса, онда

.

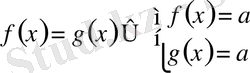• Егер, және, болса, онда

.

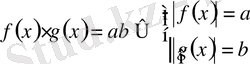Мұндағы, 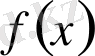және 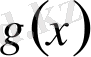бір таңбаға ие.

• Егер, және, болса, онда

.

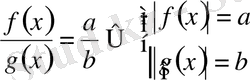Мұндағы, 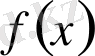және 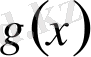бір таңбаға ие.

Есептерді шешудің мысалдары

Мысал 1. Теңдеулер жүйесін шешіңдер:

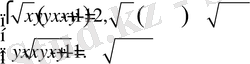
Шешуі. Түбір астындағы өрнектердің теріс болмауы шартынан, 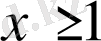және 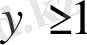шығады. Жүйенің екінші теңдеуін 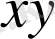бөліп:

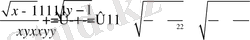
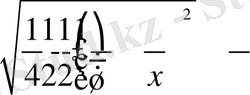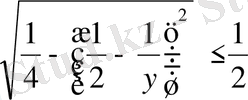және болғандықтан,

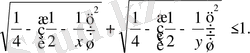
Демек, теңдік тек болған жағдайда ғана орындалады. Тексеру жасап табылған мәндер теңдеулер жүйесін қанағаттандыратынына көзімізді жеткіземіз.

Мысал 2. Функцияның ең үлкен және ең кіші мәндерін табыңыз:

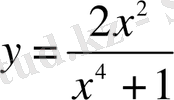
Шешуі. 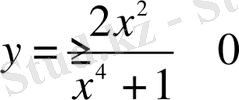және 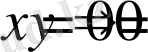екенін ескерсек, 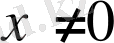жағдайын қарастырып, бөлшектің бөлімі мен алымын 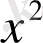бөлсек, 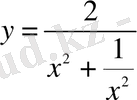аламыз. Өзара кері оң сандардың қосындысының қасиетінен 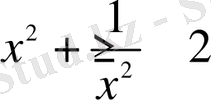аламыз, онда 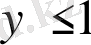және теңдік 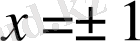үшін орындалады.

Жауабы: ; .

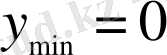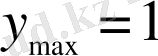Мысал 3. Өрнектің ең үлкен мәнін табыңыз:

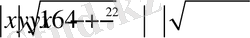
Шешуі. Есеп шартынан 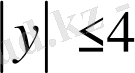және 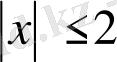шығады. Тригонометриялық ауыстыру жасаймыз:

Онда

.

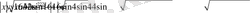
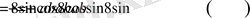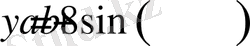функциясының ең үлкен мәні 8-ге тең болады, теңдік 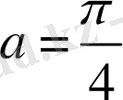және 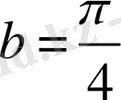орындалады. Яғни, 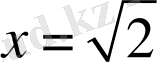және .

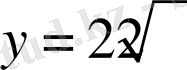Мысал 4. Теңдеуді шешіңіз:

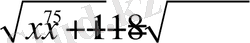
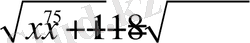
Шешуі. Түбір астындағы өрнектердің оң болу шартынан 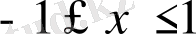аламыз. Өрнектердің анықталу облысында

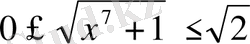және

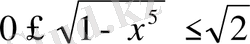
Демек, 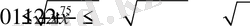, теңдеудің шешімі жоқ.

Практикалық тапсырмалар:

1. Теңдеуді шешіңіз:

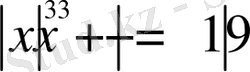
2. Теңдеуді шешіңіз:

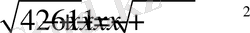
3. Теңдеулер жүйесінің барлық шешімдерін табыңыз:

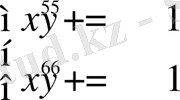
4. Теңдеулер жүйесін шешіңіз:

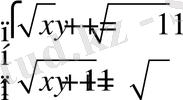
5. Теңсіздікті шешіңіз:

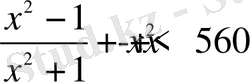
6. Функцияның ең үлкен және ең кіші мәнін табыңыз:

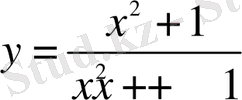
7. Функцияның мәндер жиынын табыңыз:

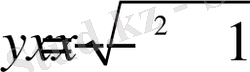
8. Функцияның ең үлкен және ең кіші мәнін табыңыз:

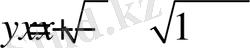
9. а параметрінің қандай мәнінде теңдеудің кемінде бір түбірі бар болады:

10. шартын қанағаттандыратын теңдеулер жүйесінің барлық шешімін табыңыз:

11. Теңдеуді шешіңіз:

12. Теңдеулер жүйесін шешіңіз:

2. Тригонометриялық теңдеулер мен теңсіздіктер

Тригонометриялық теңдеулер мен теңсіздіктерді шығаруда келесі тригонометриялық функциялардың шенелгендігін қолданамыз:

$$\left \sin x \right \leq 1, \ \ \left \cos x \right \leq 1,$$

$$\left arc\sin x \right \leq \frac{\pi}{2}, \ \ 0 \leq arc\cos x \leq \pi, \ arctgx < \frac{\pi}{2}, \ \ 0 < arcctgx < \pi$$

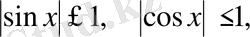
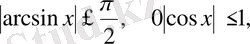
Есептерді шешудің мысалдары

Мысал 1. $x > 0$ үшін функцияның ең кіші мәнін табыңыз:

$f(x) = 4x + \frac{9\pi^{2}}{x} + \sin x.$

Шешуі: Өзара кері екі санның қосындысының қасиетін ескерсек:

$4x + \frac{9\pi^{2}}{x} + \sin x = 2 \bullet 3\pi\left( \frac{2х}{3\pi} + \frac{3\pi}{2x} \right) \geq 6\pi \bullet 2 = 12\pi, \$

мұнда теңдік $\frac{2х}{3\pi} = 1 \Longleftrightarrow x = \frac{3\pi}{2}\$ орындалады. Демек,

$x = \frac{3\pi}{2}$ болғанда, $\min_{0 < x < + \infty}\left( 4x + \frac{9\pi^{2}}{x} \right) = 12\pi.$

$x = \frac{3\pi}{2}$ болғанда $y(x) = \sin x$ функциясы да ең кіші мәніне ие болады, яғни - 1, онда

$\min_{0 < х < + \infty}f(x) = 12\pi - 1.$

Мысал 2. Теңдеуді шешіңіз:

$\sin^{2}x + 3x^{2}\cos x + 3x^{2} = 0$

Шешуі: Қосылғыштарды топтастырып

$\sin^{2}x + 3x^{2}{(cos}x + 1) = 0.$

$\cos x \geq - 1$ болғандықтан, онда теңдеудің сол жақ бөлігінде екі теріс емес өрнектердің қосындысы тұр. Ол нөлге тең болуы үшін әрбір қосылғыш жеке-жеке нөлге болуы қажет:

$$\left\{ \begin{array}{r} \sin x = 0 \\ 3x^{2}{(cos}x + 1) = 0 \end{array} \Longleftrightarrow \left\{ \begin{array}{r} \sin x = 0 \\ \left\lbrack \begin{array}{r} x = 0 \\ \cos x = - 1 \end{array} \right. \ \end{array} \Longleftrightarrow \left\lbrack \begin{array}{r} x = 0 \\ x = \pi + 2\pi n, \ \ n \in Z \end{array}. \right. \ \right. \ \right. \$$

Мысал 3. q параметрінің қандай мәнінде теңдеулер жүйесінің шешімі бар болады?

$$\left\{ \begin{array}{r} x^{2} + qx + 3 = 0 \\ \sin^{2}q\pi + \cos^{2}\frac{\pi x}{2} + 2^{y^{2}} = \sin{\frac{\pi}{2}x} \end{array} \right. \$$

Шешуі: Екінші теңдеудің сол жақ бөлігі 1-ден кем емес, ал оң бөлігі 1-ден артық емес, демек, теңдеуле жүйесі келесі жүйеге эквивалентті:

$$\left\{ \begin{array}{r} x^{2} + qx + 3 = 0 \\ \sin{q\pi} = 0 \\ \cos\frac{\pi x}{2} = 0 \\ y = 0 \\ \sin{\frac{\pi x}{2} = 1} \end{array} \Longleftrightarrow \left\{ \begin{array}{r} x = \frac{- q \pm \sqrt{q^{2} - 12}}{2} \\ q \geq 12 \\ q \in Z \\ y = 0 \\ x = 1 + 4n, \ n \in Z \end{array} \right. \ \right. \$$

Бірінші және соңғы теңдеуден келесіні аламыз:

$${(2(1 + 4n) + q) }^{2} = q^{2} - 12 \Longleftrightarrow q = - \frac{3}{1 + 4n} - (1 + 4n)$$

$q \in Z$ болғандықтан, бөлшектің бөлімі келесі төрт мәннің біріне тең болады:

1. 1+4n=−3⇔n=−1. 1 + 4n = - 3 \Longleftrightarrow n = - 1. Бұл жағдайда, q=4, x=−3, y=0. q = 4, \ x = - 3, \ y = 0.
2. 1+4n=−1⇔n=−0, 5. n∈Z1 + 4n = - 1 \Longleftrightarrow n = - 0, 5. \ n \in Zболғандықтан, жарамайды.
3. 1+4n=1⇔n=0. 1 + 4n = 1 \Longleftrightarrow n = 0. Бұл жағдайда, q=−4, x=1, y=0. q = - 4, \ x = 1, \ y = 0.
4. 1+4n=3⇔n=0, 5∉Z. 1 + 4n = 3 \Longleftrightarrow n = 0, 5 \notin Z.

Мысал 4. Кез-келген $x > 0$ үшін келесі теңсіздікті дәлелдеңіз:

$$x^{2} + \pi x + \frac{15}{2}\pi\sin{x > 0}$$

Шешуі . $f_{1}(x) = \sin{x\ }$ функциясының шенелгендігін ескерсек, келесі бағалау орындалады:

$$x^{2} + \pi x + \frac{15}{2}\pi\sin x \geq x^{2} + \pi x - \frac{15}{2}\pi$$

$f_{2}(x) = x^{2} + \pi x - \frac{15}{2}\pi$ қарастырайық. Бұл квадрат үшмүшенің түбірлері

$$x_{1, 2} = \frac{\pm \sqrt{\pi^{2} + 30\pi} - \pi}{2}$$

Демек, $0 < x < \frac{\sqrt{\pi^{2} + 30\pi} - \pi}{2}$ үшін $f_{2}(x) < 0, \$ ал $x > \frac{\sqrt{\pi^{2} + 30\pi} - \pi}{2}$ үшін $f_{2}(x) > 0$

1) $\frac{\sqrt{\pi^{2} + 30\pi} - \pi}{2} < \frac{7\pi}{6}$ екенін байқайтын болсақ, бұл теңсіздік $x > \frac{7\pi}{6}$ үшін орындалады. Ал х-тің қалған мәндері үшін екі жағдайды қарастырамыз.

2) $х \in (0; \ \pi)$ үшін теңсіздіктің сол жақ бөлігінде екі оң мән қабылдайтын функциялардың қосындысы орналасқан, яғни, $g(x) = x^{2} + \pi x > 0$ және $h(x) = \frac{15\pi}{2}\sin x > 0,$ демек қарастырылып отқан аралықта теңсіздік орындалады.

3) $х \in \left\lbrack \pi; \ \frac{7\pi}{6} \right\rbrack$ болсын . $g(x)$ және $h(x)$ функцияларын төменнен бағалайтын болсақ

$g(x) = x^{2} + \pi x > 2\pi^{2} > 4\pi;$

$h(x) = \frac{15\pi}{2}\sin x > \frac{15\pi}{2} \bullet \left( - \frac{1}{2} \right) = - \frac{15\pi}{4} > - 4\pi.$

Демек, қосынды үшін келесі бағалау орынды

$g(x) + \ h(x) > 4\pi - 4\pi = 0$

Барлық жағдайларды біріктіретін болсақ, $x > 0$ үшін теңсіздіктің орындалатынына көз жеткіземіз.

3. Құрамында логарифмдік және көрсеткіштік функциялары бар теңдеулер мен теңсіздіктер

Логарифмдік және көрсеткіштік функциялардың шенелгендігін қолдану арқылы теңдеулер мен теңсіздіктерді шешуде бұған дейінгі тақырыптарда қарастырылған қасиеттер орындалады.

Есептерді шешудің мысалдары

Мысал 1. р параметрінің қандай мәндерінде теңдеудің шешімдері бар болады:

$$4^{x} + 2^{x + 2} + 7 = р - 4^{- x} - 2 \bullet 2^{1 - x}$$

Шешуі. Теңдеуді келесі түрде жазамыз

$$\left( 4^{x} + \frac{1}{4^{x}} \right) + 4\left( 2^{x} + \frac{1}{2^{x}} \right) + 7 = p$$

Өзара кері сандардың қосындысының қасиеті бойынша

$$4^{x} + \frac{1}{4^{x}} \geq 2, \ \ 2^{x} + \frac{1}{2^{x}} \geq 2$$

Теңдік екі жағдайда да $x = 0\$ болғанда орындалады, онда теңдеудің сол жақ бөлігіндегі өрнек $2 + 4 \bullet 2 + 7 = 17\$ кем мән қабылдамайды, демек, функция үзіліссіз болғандықтан, 17-ден үлкен немесе оған тең мәндер қабылдайды. Теңдеудің шешімі $p \geq 17$ орындалады.

Мысал 2. Теңдеуді шешіңіз:

$$25 \bullet 3^{x - 5 + x - 3} + 9 \bullet x^{x - 4 + x - 6} = 450$$

Шешуі. Теңдеудің екі жақ бөлігінде бөлеміз

$$3^{x - 5 + x - 3 - 2} + 5^{x - 4 + x - 6 - 2} = 2$$

х кез келген мәні үшін келесі теңсіздіктер орындалады

$$x - 3 + x - 5 \geq 2; \ \ x - 4 + x - 6 \geq 2;$$

Онда, теңдеудің сол жақ бөлігі оң жақ бөлігінен үлкен немесе тең болады, теңдік тек келесі жағдайда орындалады:

$$\left\{ \begin{array}{r} x - 3 + x - 5 = 2 \\ x - 4 + x - 6 = 2 \end{array} \Leftrightarrow \left\{ \begin{array}{r} x - 3 \geq 0 \\ x - 5 \leq 0 \\ x - 4 \geq 0 \\ x - 6 \leq 0 \end{array} \Leftrightarrow 4 \leq x \leq 5 \right. \ \right. \$$

Мысал 3. Теңдеуді шешіңіз:

$$\ln x + \frac{1}{\ln x} = 2 \bullet \sin\left( x + \frac{\pi}{4} \right)$$

Шешуі. $\left \ln x + \frac{1}{\ln x} \right \geq 2$ және $\left 2 \bullet \sin\left( x + \frac{\pi}{4} \right) \right \leq 2$ болғандықтан, теңдеудің сол жақ және оң жақ бөліктерінің тең болуы үшін екі жағы да 2-ге тең болуы керек.

Бірінші жағдайда,

$$\left\{ \begin{array}{r} \ln x + \frac{1}{\ln x} = 2 \\ 2 \bullet \sin\left( x + \frac{\pi}{4} \right) = 2 \end{array} \Leftrightarrow \left\{ \begin{array}{r} \ln x = 1 \\ \sin\left( x + \frac{\pi}{4} \right) = 1 \end{array} \Leftrightarrow \left\{ \begin{array}{r} x = e \\ x = \frac{\pi}{4} + 2\pi n, \ n \in Z \end{array} \Leftrightarrow \varnothing \right. \ \right. \ \right. \$$

Екінші жағдайда,

$$\left\{ \begin{array}{r} \ln x + \frac{1}{\ln x} = - 2 \\ 2 \bullet \sin\left( x + \frac{\pi}{4} \right) = - 2 \end{array} \Leftrightarrow \left\{ \begin{array}{r} \ln x = - 1 \\ \sin\left( x + \frac{\pi}{4} \right) = - 1 \end{array} \Leftrightarrow \left\{ \begin{array}{r} x = e^{- 1} \\ x = - \frac{3\pi}{4} + 2\pi n, \ n \in Z \end{array} \Leftrightarrow \varnothing \right. \ \right. \ \right. \$$

Демек, теңдеудің шешімі жоқ.

Мысал 4. Теңсіздікті шешіңіз:

$$\log_{0, 5}1 - x - \log_{x - 1}2 \leq 2$$

Шешуі Теңсіздікте берілген екінші логарифмдік функцияның негізіндегі шектеулерді қолданып бірінші логарифмдік функцияда берілген модульді ашсақ, және жаңа неігізге көшу формуласын қолдансақ

$$\log_{2}{(x - 1) } + \frac{1}{\log_{2}{(x - 1) }} \geq - 2$$

Өзара кері сандардың қосындысының қасиеті бойынша теңсіздік келесі теңсіздіктер жиынтығына эквивалентті болады:

$$\left\lbrack \begin{array}{r} \log_{2}{(x - 1) } > 0 \\ \log_{2}{(x - 1) } = - 1 \end{array} \Leftrightarrow \left\lbrack \begin{array}{r} x - 1 > 1 \\ x - 1 = \frac{1}{2} \end{array} \Leftrightarrow \left\lbrack \begin{array}{r} x > 2 \\ x = \frac{3}{2} \end{array} \Leftrightarrow \left\{ \frac{3}{2} \right\} \right. \ \right. \ \cup (2; \ + \infty) \right. \$$

Мысал 5. Теңсіздікті шешіңіз:

$$2^{\sin x} + 2^{\cos x} \geq 2^{1 - \frac{\sqrt{2}}{2}}$$

Шешуі: Теңсіздіктің сол жақ бөлігін бағалайық

$$2^{\sin x} + 2^{\cos x} \geq 2\sqrt{2^{\sin x} + 2^{\cos x}} = 2^{1 + \frac{1}{2}\left( \sin x + \cos x \right) } = 2^{1 + \frac{\sqrt{2}}{2}\sin\left( x + \frac{\pi}{4} \right) }$$

4. Рационалдау әдісі

Рационалдау әдісі - бұл белгілі жағдайларда теңсіздіктерді жеңілдетудің, яғни теңсіздіктерді рационал теңсіздікке айналдырудың әдісі, ал рационал теңсіздікті интервалдар әдісімен қолданып шешеміз.

f(x) - монотонды өспелі функциясы берілсін. а және b сандары берілген функцияның анықталу облысына тиісті болсын, онда келесі тұжырымдар ақиқат болады:

• f(a) >f(b) f(a) > f(b) теңсіздігіа>bа > bтеңсіздігі эквивалентті, немесе басқаша айтқандаf(a) −f(b) >0f(a) - f(b) > 0теңсіздігіа−b>0а - b > 0теңсіздігіне эквивалентті болады.
• Осылайша, f(a) <f(b) ⇔а<bf(a) < f(b) \Leftrightarrow а < bнемесеf(a) −f(b) <0⇔а−b<0f(a) - f(b) < 0 \Leftrightarrow а - b < 0

Осы екі тұжырымды қысқаша жазатын болсақ:

Егер f(x) - монотонды өспелі функция болса, онда $f(a) - f(b)$ айырымының таңбасы $a - b$ айырымының таңбасымен бірдей болады.

Теңсіздіктерді шешуде бұл идеяның қолданылуын келесі мысал арқылы көрсетуге болады:

$\frac{f(x) - f(a) }{g(x) - g(b) } > 0$ (1)

мұндағы, $f(x)$ және $g(x)$ - монотонды өспелі функциялар . Онда $f(x) - f(a)$ айырымын $x - а$ айырымына ауыстыруға, ал $g(x) - g(b)$ айырымын $x - b$ айырымына ауыстыруымызға болады. Келесі рационал теңсіздікті аламыз:

$\frac{x - a}{x - b} > 0$ (2)

Бұл теңсіздікті интервалдар әдісімен шешеміз. Мұндағы (2) теңсіздік (1) теңсіздіктің салдары болады. Демек, (2) теңсіздіктің шешімдерінің ішінде (1) теңсіздіктің барлық шешімдері жатады, арасында бөгде түбірлері де болуы мүмкін. Теңсіздіктің шешімін таңдап алу үшін, $f(x)$ және $g(x)$ функцияларының анықталу облыстарымен қиылыстырсақ жеткілікті.

Есептерді шешудің мысалдары

Мысал 1. Теңсіздікті шешіңіз:

$$\log_{x^{2}}(x + 2) < 1$$

Шешуі. Теңсіздікте қандай да бір тұрақты негізге көшейік. Мысалы, негізі 10 логарифмі

$$\frac{{lg}(x + 2) }{\lg x^{2}} < 1$$

Рационалдау әдісін қолдану үшін, теңсіздіктің оң жағында нөл болуы қажет. Бірді сол жаққа көшіреміз:

$$\frac{{lg}(x + 2) }{\lg x^{2}} - 1 < 0 \Leftrightarrow \frac{{lg}{(x + 2) - \lg x^{2}}}{\lg x^{2}} < 0$$

Бөлшектің алымнда логарифмдердің айырымы шықты. Бөлшектің бөлімінде де логарифмдердің айырымы қажет. Бұл айырымды оңай алуымызға болады:

$$\lg x^{2} = \lg x^{2} - 0 = \lg x^{2} - \lg 1$$

Осылайша, теңсіздік келесі түрде ие болады:

$$\frac{{lg}{(x + 2) - \lg x^{2}}}{\lg x^{2} - \lg 1} < 0$$

Бұған дейін теңсіздікте теңбе тең түрлендірулер қолданылған болатын, демек, теңсіздік берілген теңсіздікке мәндес теңсіздік болады.

Енді $y = lgx$ функциясының монотонды өспелі екенін ескерсек, теңсіздік келесі теңсіздіктер жүйесіне көшеді:

... жалғасы

Жаратылыстану-математика сыныптарында оқытылатын математиканың элективтік курстарының мазмұны

Логарифмдік теңдеулерді шешу

Жаратылыстану-математикалық бағытта бейіндік оқытудың әдістемелік ерекшеліктері

Айнымалысы модуль ішіндегі теңсіздіктер

Мектеп математика курсында функцияны оқытудың мақсаттары

Мектеп математика курсындағы теңдеулер мен теңсіздіктерді оқыту әдістемесі

Математиканы тереңдетип окыту

Математикадан сыныптан тыс сабақтар

Химияны жаратылыстану ғылымдарымен байланыстыра оқытудың ерекшеліктері

Анықталмаған интеграл қасиеттері

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс