ПРОГРЕССИЯНЫҢ ҚОСЫНДЫЛАРЫН ЕСЕПТЕУДЕ ГЕОМЕТРИЯЛЫҚ ӘДІСТЕРІН ҚОЛДАНУ

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 14 бет
Таңдаулыға:

Ақтөбе облыстық мамандандырылған физика-математикалық мектеп-интернат

ПРОГРЕССИЯНЫҢ ҚОСЫНДЫЛАРЫН ЕСЕПТЕУДЕ

ГЕОМЕТРИЯЛЫҚ ӘДІСТЕРІН ҚОЛДАНУ

Секциясы: Математика

Дайындаған: Акимгереева Шадияра 10 класс

Саламатова Фарида 10 класс

Ғылыми жетекшісі: Иманчиев Асқарбек Ермекұлы

Физика-математика ғылымдарының кандидаты, Қ. Жұбанов атындағы АӨУ доценті

Жетекшісі: Таңатарова Ұштап Бақтығалиқызы, Арызахметов Еркебулан Алтынбекулы

Математика пәні мұғалімдері

2021 жыл

Аннотация

Ғылыми зерттеудің мақсаты: Арифметикалық және геометриялық прогрессиялардың қосындыларын табудың геометриялық жолдарын табу, прогрессияларды зерттеу әдістері кеңейту.

Гипотезасы: Тұрақты айырымды прогрессиялардың қосындыларын табуда геометрияның негізгі ұғымдары ұзындық, аудан, көлем сынды ұғымдармен геометрияның кеңінен қолданылатын теоремаларды ұштастырып, қосындылауға пайдалану. Жобамыздағы басты гипотеза ретінде, кез-келген арифметикалық, геометриялық бірінші ретті және одан реті жоғары прогрессиялардың қосындыларын табуға геометрия әдістерін пайдалануға болатындығы.

Зерттеу барысында, алдымен арифметикалық прогрессияның қосынды формуласын геометриялық жолмен алған болатынбыз. Бұл тұста, Фалес теоремасы, пропорционал кесінділер туралы теоремалар сынды геометриялық белгілі тұжырымдар қолданылды, ал келесі кезекте геометриялық прогрессия қосындысын алу барысында аудан ұғымдары кеңінен қолданылды. Осылайша жұмыста табиғаттары басқа болғанмен математиканың бөлімдерінің бір-бірімен тығыз байланысы айқын байқалды.

Зерттеу нәтижелерін олимпиадалық есептерді шешу барысында, прогрессияның визуалды көрсету мүмкіндігін ашады.

Abstract

The purpose of the research : to find geometric ways to find the sum of arithmetic and geometric progressions, to expand the methods of studying progressions.

Hypothesis: The use of the basic concepts of geometry in the combination of the most widely used theorems of geometry, such as length, area, volume, in finding the sum of constant differential progressions. The main hypothesis of our project is that geometric methods can be used to find the sum of any arithmetic, geometric first order and higher progressions.

In this case, geometrically known concepts such as Thales' theorem, theorems on proportional segments were used, and then the concept of area was widely used in obtaining the sum of geometric progressions. Thus, in the work, despite the different nature, it is clear that the sections of mathematics are closely related to each other.

The results of the study reveal the possibility of visual representation of progress in solving Olympic problems.

Бұл жұмыста арифметикалық және геометриялық прогрессиялардың n алғашқы мүшелерін қосындылаудың геометриялық жолдары жайлы зерттеу жүргізіледі.

1. Осындай геометриялық прогрессияның мүшелерін алудың қызықты геометриялық жолын көрсетейік: a, a ² , a ³ , a ⁴ , . . .

Ox және Oy өзара перпендикуляр екі түзуді құрайық.

О нүктесінен Ох осінің бойындмен ОА = 1 кесіндісін, ал Оу осінің бойымен ОВ = а кесіндісін кейінге қалдырамыз.

Біз А нүктесін В нүктесімен АВ кесіндісімен байланыстырамыз және В нүктесінен осы перпендикулярды қалпына келтіреміз. Бұл перпендикуляр Ох осін С нүктесінде қиып өтеді; осы нүктеден перпендикулярды ВС ға қайтадан қалпына келтіріңіз және т. б.

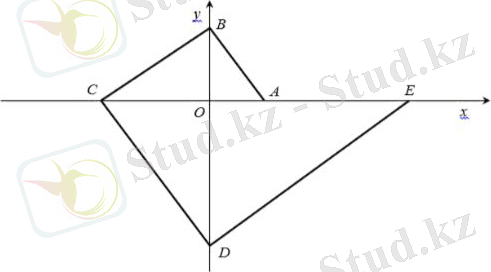
$C:\Users\Acer\Downloads\1 сурет.jpg$

OС = a ² , ОД = а ³ , ОЕ = а ⁴ және т. б екенін дәлелдейік

Тік бұрыштың төбесінен гипотенузаға дейінгі перпендикуляр теоремасы бойынша бізде

ОА × ОС= (ОВ) ² , яғни OC = a ²

ОВ × ОД = (ОC) ² , яғни OD = a ³ ,

OC × OE = (OD) ² , яғни OE = a ⁴ , және т. c. c.

2. Геометриялық жолмен берілген геометриялық прогрессияның тағы бір мысалын қарастырайық.

α ға тең сүйір AOB бұрышын алыңыз

ОА = 1. болсын А нүктесінен АВ перпендикулярын ОВ түзуіне түсірейік, онда ОС = cosα.

СD⊥OA жүргізейік, содан кейін бізде екі ұқсас үшбұрыш болады: OCAOC және ∆ADS. Ұқсастықтан

біз алатын үшбұрыштар $\frac{ОД}{ОС}$ = $\frac{ОС}{ОА}$ ОА = 1, OC = cosα екенін ескере отырып, OD = cos2α аламыз.

Перпендикулярларды DE, EF және т. біз OE = $\cos^{3}$ α, OF = $\cos^{4}$ α және т. б.

$C:\Users\Acer\Downloads\2 сурет.jpg$

Сонымен, бізде cosα, $\cos^{2}$ α, $\cos^{3}$ α, $\cos^{4}$ α, . . . тізбегі бар . . . Егер α орнына кез келгенін алсақ мәні болса, онда біз сәйкес сандық тізбекті аламыз. Мысалы:

α= $\frac{\pi}{4}$ : cos $\frac{\pi}{4}$ , ${(\cos\frac{\pi}{4}) }^{2}$ , ${(\cos\frac{\pi}{4}) }^{3}$ , ${(\cos\frac{\pi}{4}) }^{4}$ , . . . немесе $\frac{\sqrt{}2}{2}$ , $\frac{1}{2}$ , $\ \frac{\sqrt{}2}{4}$ , $\ \frac{1}{4}$ , $\ \frac{\sqrt{}2}{8}$ , . . .

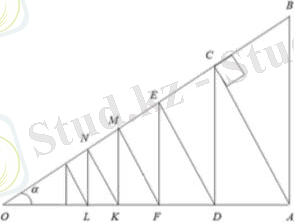
3. ВОА -ның үшкір бұрышын алыңыз, α -ге тең. Осыдан AC⊥OB, CD⊥OA, CR⊥AB, KH⊥OB, HM⊥AB және т. б. жүргіземіз.

$C:\Users\Acer\Downloads\3 сурет.jpg$

Үшбұрыштардың ұқсастығынан ∆OAC және ∆ASD $\frac{AD}{AC} = \frac{AC}{OA}$ алды. ОА = 1, АС = sin $\alpha$ , екенін ескере отырып CK = АD= $\sin^{2}\alpha$ аламыз.

$\mathrm{\Delta}$ СНК мен $\mathrm{\Delta}$ СКА ұқсастығынан біз $\frac{HK}{KC}$ $= \frac{KC}{AC}\$ алдық. $\mathrm{\Delta}$ OСA мен $\mathrm{\Delta}$ СKA ұқсастығынан біз $\ \frac{КС}{АС}$ $= \frac{АС}{АО}\$ алдық. Соңғы екі теңдіктен бізде $\frac{HK}{CK} = \frac{AC}{AO}$ бар.

OA = 1, CK = $\sin^{2}\alpha$ , AC= sin $\alpha$ , бізде НК = $\sin^{3}\alpha$ бар. Сол сияқты, НМ = $\sin^{4}\alpha$ және т. б.

Сонымен, бізде sin $\alpha$ , $\sin^{2}\alpha$ , $\sin^{3}\alpha$ , $\sin^{4}\alpha$ , . . . прогрессиясы бар.

4. Паскаль үшбұрышының әрбір көлденең сызығындағы сандар геометриялық прогрессияның мүшелері болатын есеп, қызықты болып табылады. Шын мәнінде:

1 = $2^{0}$

1 + 1 = $2^{1}$

1 + 2 + 1 = $2^{2}$

1 + 3 + 3 + 1 = $2^{3}$

1 + 4 + 6 + 4 + 1 = $2^{4}$

. . .

Бізде b ₁ = 1 бірінші мүшесі мен q = 2 еселігі бар геометриялық прогрессия пайда болады.

5. Шеңберді (4 -сурет) тең доғалардың белгілі бір санына AM, MN, NP, HQ және т. б. бөлінсін.

A, M, N, P, Q нүктелері және т. б. шеңбердің радиусы болатын кесінділер арқылы О нүктесіне қосамыз. А нүктесінен АМ` перпендикулярын ОМ радиусына түсірейік; М` нүктесінен M`N` перпендикулярын түсіреміз және т. д.

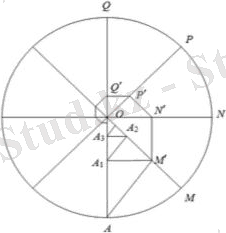
$C:\Users\Acer\Downloads\4 сурет.jpg$

Пайда болған AM`N`P`Q` . . . сынық сызықтардың ұзындықтары қайсыбір геометриялық прогрессияның қосындысына тең болатынына көзіміз жетеді. Мысалы, шеңбер радиусын 1-ге тең деп алып, ал шеңберді алдымен 6, сонан соң, 8, одан кейін 12 бөлікке бөлетін болсақ, сынық сызықтардың геометриялық прогрессия қосындысын беретінін байқаймыз.

Нұсқау ретінде сізге бұл үзік сызықтың ұзындығы AM`A ₁ A ₂ A ₃ A ₄ . . . үзік сызығының ұзындығына тең болатынын ескергеніміз жөн. Алдымен AM`, A ₁ A ₂ , A ₃ A ₄ , . . . және A ₁ M`, A ₃ A ₂ , A ₅ A ₄ , . . . сегменттерінің ұзындықтары бірдей еселігі бар геометриялық прогрессия мүшелерін құрайтынын алдын-ала дәлелдеп алуымыз қажет. Шеңбер 6 тең доғаға бөлінсе, прогрессияның қосындысы $\sqrt{3}$ болады, 8 тең бөлікке бөлінген жағдайда (1 + $\sqrt{2}$ ), 12 тең доғаға бөлінген жағдайда - (2 + $\sqrt{3}$ ) болатынын ескереміз.

Бірінші жағдайда бізде бірінші мүшесі b ₁ = $\frac{\sqrt{3}}{2}$ геометриялық прогрессия болады және q ₁ = $\frac{1}{2}$ еселігі, екінші жағдайда b ₁ = $\frac{\sqrt{2}}{2}$ , q ₂ = $\frac{1}{\sqrt{2}}$ , үшінші жағдайда b ₁ = $\frac{\sqrt{}2}{2}$ , q ₃ = $\frac{\sqrt{3}}{2}$ , осындай геометриялық прогрессиялар пайда болады.

Кемімелі геометриялық прогрессия

Кемімелі геометриялық прогрессияның алғашқы екі мүшесі берілсін. Оның басқа мүшелерін геометриялық түрде қалай табуға болатынын көрсетейік.

Прогрессияның бірінші мүшесіне тең AB` кесіндісін саламыз . А және В нүктелері арқылы біз O нүктесінде қиылысатын Ox және Oy кез-келген түрде алынған екі түзуді жүргіземіз, AB` бойынша прогрессияның екінші мүшесіне тең KB` кесіндісін сызып аламыз. Оy-ке параллель К нүктесі арқылы түзу жүргіз. Осы түзудің Ox түзуімен қиылысу нүктесі арқылы AB` параллель түзуді жүргіземіз; онда С` нүктесі арқылы - В`В параллель және т. с. с.

Сонда $\frac{BC`}{AB`}$ = $\frac{OB}{OA}$ = $\frac{OC`}{OB`}$ = $\frac{OC}{OB}$ = $\frac{CD`}{BC`}$ = . . . Бұл осы прогрессия мүшелері тең болатынын білдіреді.

AB`, BC`, CD`, DE`, EM` сегменттері және т. б. Бұл прогрессияның еселігі q = $\frac{OC`}{OD`}$

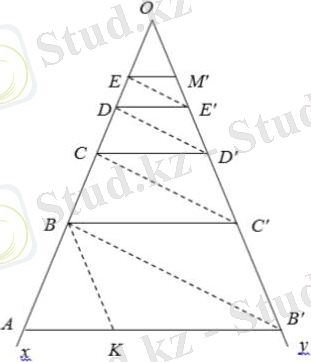
$C:\Users\Acer\Downloads\5 сурет.jpg$

Жоғарыда айтылғанның негізінде, кемімелі геометриялық прогрессияның кез келген мүшелері санының қосындысын оңай таба аламыз. СС`, DD`, EE`… желісін ұзарту жеткілікті, C``, D``, E`` нүктелерінде АВ` кесіндісінде қиылыспағанға дейін. АС``, AD``, AE`` бұл екі, үш және төрт мүшенің қосындысы прогрессиясы қосындылары оңай дәлелдей алады. Егер О нүктесі арқылы АВ` кесіндісінің жалғасуымен қиылысқанға дейін O`` нүктесіндегі түзу OO`` түзу сызық салынса., параллельдік тікелей ВВ′, онда AO`` кесіндісін аламыз, ол геометриялық прогрессияның шексіз кемуі қосындының мүшелерін білдіреді:

AO``=AB`+BC`+CD`+DE`+… 6-суретте тағы бір шексіз кемитін геометриялық прогрессия көрсетілген, еселік q = $\frac{OC`}{OB`}$ , бірақ алғашқы мүшесі өзгеше.

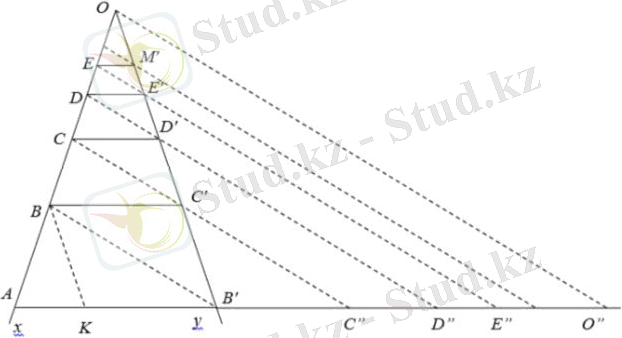
$C:\Users\Acer\Downloads\6 сурет.jpg$

Мына суреттен бізде $\frac{CC`}{BB`}$ = $\frac{OC`}{OB`}$ = $\frac{OC}{OB}$ = $\frac{OD`}{OC`}$ = $\frac{DD`}{CC`}$ = . . .

бұл BB’, CC’, DD’, EE’, . . . сонымен қатар шексіз кемитін геометриялық прогрессияның мүшелері.

Осы прогрессия мүшелерінің қосындысы OO” кесіндісіне тең екенін дербес дәлелдеуге болады. Бұны қосымша орындауға болатын тапсырма ретінде қарастыруға болады.

Мүшелер саны шексіз $\frac{1}{2}$ , $\frac{1}{4}$ , $\frac{1}{8}$ , $\frac{1}{16}$ , . . . геометриялық прогрессиясының қосындысы 1-ге тең екені белгілі.

Графикалық түрде бұл прогрессияны келесі түрде ұсынуға болады.

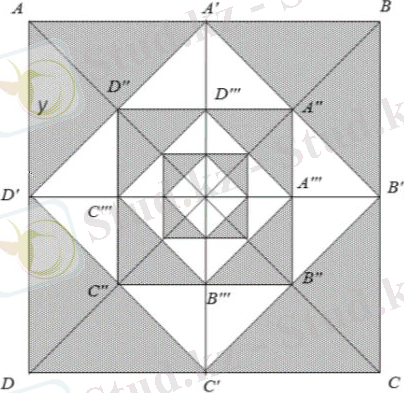
$C:\Users\Acer\Downloads\7 сурет.jpg$

Қабырғасы 1 -ге тең бірінші AВСД квадратында, оның төбелері бірінші квадраттың қабырғаларын жартысына бөлетін нүктелерге жататындай екіншісін жазамыз. Үшбұрыштардың аудандарының қосындысы

AA’D’+BB’A’+CC’B’+DD’C’

ABCD квадратының жартысына тең екенін дәлелдеу оңай, яғни $\frac{1}{2}$ . АА”Д”+AА”В’В”+B”C’C”+C”D’D”үшбұрыштарының аудандарының қосындысы ABCD квадратының $\frac{1}{4}$ ауданына тең және т. б.

Бұл прогресті шексіздікке жалғастыра отырып, шектіде біз 1 -ге тең AВСД бастапқы квадратының бүкіл ауданын аламыз.

Шексіз кемитін $\frac{1}{4}$ , $\frac{1}{16}$ , $\frac{1}{64}$ , . . . геометриялық прогрессияның геометриялық қосындысын табайық. АВС үшбұрышын алайық, оның ауданы бірге тең. D және E нүктелері сәйкесінше AC және AB жақтарының орта нүктелері болып табылады; ВД В төбесінен төмен түсірілген медиана болады. Біз D және E нүктелерін қосамыз және АС түзуіне параллель ЕF түзуін және ДЕ-ге параллель FK түзулерін жүргіземіз және т. б.

$C:\Users\Acer\Downloads\8 сурет.jpg$

Мына суреттен көлеңкеленген үшбұрыштардың ADE, EFK, KHM, MON және т. б. аудандары $\frac{1}{4}, \frac{1}{16}, \frac{1}{64}$ , . . . $\mathrm{\Delta}$ ABC үшбұрышының бөліктерінің аудандарына тең болады.

$S_{\mathrm{\Delta}ADE} + S_{\mathrm{\Delta}EFK} + S_{\mathrm{\Delta}KHM} + S_{\mathrm{\Delta}MON} + . . .$ олардың аудандарының қосындысы $\frac{1}{3}$ -ге тең болады, өйткені

$S_{\mathrm{\Delta}ADE} = \frac{1}{3}S_{AELC}$ , $S_{\mathrm{\Delta}EFK} = \frac{1}{3}S_{EKPH}$ және т. б.

Демек $S_{\mathrm{\Delta}ADE} + S_{\mathrm{\Delta}EFK} + S_{\mathrm{\Delta}KHM} + S_{\mathrm{\Delta}MON} + . . . = \frac{1}{3}S_{\mathrm{\Delta}ABC}$

ал $S_{\mathrm{\Delta}ABC} = 1$ болғандықтан, бұл қосынды $\frac{1}{3}$ -ке тең.

9. 1, 4, 7, 10, 13, 16 арифметикалық прогрессияның қосындысын табыңыз.

$C:\Users\Acer\Downloads\9 сурет.jpg$

Біріншіден, бұл прогрессияны 16, 13, 10, 7, 4, 1 кему ретпен жазыңыз. Бірінші қатарда 1 көлеңкеленген ұяшық пен 16 көлеңкесі жоқ ұяшық, екіншісінде - көлеңкелі 4 ұяшық пен 13 көлеңкесі жоқ ұяшық және т. б.

Әлбетте, мүшелердің қосындысы көлеңкелі немесе көлеңкесі жоқ ұяшықтардың санына тең, сондықтан осылайша түзілген төртбұрыш ұяшықтарының жартысы; бұл қосынды 6 ∙ (16 + 1),

бұл 1, 4, 7, 10, 13, 16 прогрессия мүшелерінің қосындысы

$\frac{6 \bullet (16 + 1) }{2}$ =51

-ге тең болады дегенді білдіреді. Қажетті соманы келесі суреттегі көрсетілгендей геометриялық түрде табуға болады. 1 + 4 + 7 + 10 + 13 + 16 = (16 + 1) • 3 = 51.

$C:\Users\Acer\Downloads\12 cehtn.jpg$

Келесі арифметикалық прогрессия қосындысын, қосымша тапсырма ретінде қарастыруға болады:

n дәл осылай табуды ұсынамыз сандарды 1 + 2 + 3 + . . . + n.

Алғашқы тоғыз тақ санның қосындысын табыңыз.

Қабырғасы 9 -ға тең квадрат сызайық. Квадратта суретте көрсетілгендей бояйық.

Ежелгі гректер бұл Г-тәрізді фигураларды гномондар деп атаған . Ішіндегі квадраттар санын санау сандар әрбір гном бізде 1, 3, 5, 7, 9, 11, 13, 15, 17 реттік болады - бұл тақ сандар тізбегі. Олардың қосындысын квадраттарды қайта есептеместен AВСД квадратының ауданы ретінде табуға болады.

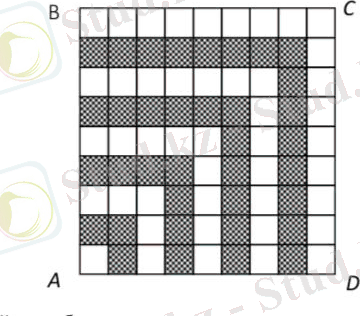
$C:\Users\Acer\Downloads\10 сурет.jpg$

1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 = 81

Бұл нәтижені қорытындылай келе, біз бірінші тақ сандардың қосындысын есептейтін формуланы аламыз: 1 + 3 + 5 + 7 + . . . + (2n‒ 1) = n ² .

11. Осындай тізбектің k мүшесінің қосындысын есептейік

$1^{3}$ , $2^{3}$ , $3^{3}$ , . . . , $k^{3}$ , яғни k натурал сандар кубтарының қосындысы.

AВСD квадратының қабырғалары 1 + 2 + 3 + . . . + k қосындысына тең. А шыңындағы бұл шаршыда біз қабырғалары бар квадраттар сериясын құрамыз: 1, (1 + 2), (1 + 2 + 3), . . . , (1 + 2 + 3 + . . . + k) . Ені k -ке тең гномон ВСДД`С`В` ауданы бар:

S BCD`S`B` = S BB`FС + S ДД`СE‒ S СЕС`F = 2 kAD - k ² .

AD - 1 + 2 + 3 + . . . + k арифметикалық прогрессияның қосындысы және $\frac{k(k + 1) }{2}$ -ге тең, сондықтан гномон ауданы ВСDD`С`В` бұл: $k^{2}$ (k + 1) ‒ $k^{2}$ = $k^{3}$ .

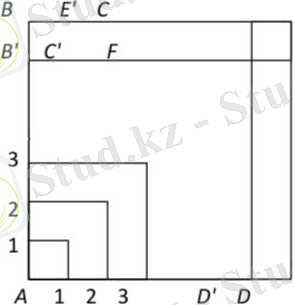
$C:\Users\Acer\Downloads\11 сурет.jpg$

Сондықтан суретте көрсетілген гномондардың ауданы болады: $1^{3}$ , $2^{3}$ , $3^{3}$ , . . . , $k^{3}$ . Олардың қосындысы - қабырғасы 1 + 2 + 3 + . . . + k тең квадрат. Бұл натурал қатардағы сандардың кубтарының қосындысы осы сандардың қосындысының квадратына тең екенін білдіреді, яғни

$1^{3}$ , $2^{3}$ , $3^{3}$ , . . . , $k^{3}$ = ${(\frac{k(k + 1) }{2}) }^{2}$ натурал сандардың текшелерін білдіреді.

Екі бұрыштың қосындысының синусы

Қазір танымал тригонометриялық формулалардың бірі болып табылатын екі бұрыштың қосындысының синусын дәлелдейік:

$\sin(\alpha + \beta) = \sin{\alpha\cos{\beta + \sin{\beta\cos\alpha}}}$

Тіктөртбұрыштың ішінде гипотенузасы 1 болатын екі жұп бірдей тікбұрыштың үшбұрыштыр орналасқан. Жасыл үшбұрыштардың бұрышы $\alpha$ , ал қызылдары $\beta.$ Ортада бұрышы $\alpha + \beta$ болатын ромб салынғанын байқай аламыз.