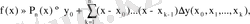Функцияны жуықтау және интерполяция әдістері: Лагранж пен Ньютон формулалары, шекті айырымдар және кубикалық сплайндар


№10-11 дәріс
Функцияны жуықтау әдістері. Лагранждың интерполяциялық формуласы. Ньютонның интерполяциялық формулалары.
Айталық
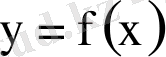 , берілген функция болсын.
, берілген функция болсын.
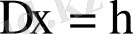 арқылы аргумент өсімшесініңбекітілген шамасын белгілеп аламыз. Онда
арқылы аргумент өсімшесініңбекітілген шамасын белгілеп аламыз. Онда
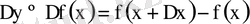
өрнегі
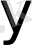 функциясының бірінші шекті айырымы деп аталады. Жоғарғы ретті шекті айырымдар жоғарғыдағыдай анықталады.
функциясының бірінші шекті айырымы деп аталады. Жоғарғы ретті шекті айырымдар жоғарғыдағыдай анықталады.
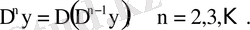
Интерполяция есебі келесідей болады:
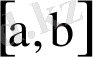 интервалында интерполяция түйіндері деп аталатын
интервалында интерполяция түйіндері деп аталатын
 нүктелер
нүктелер
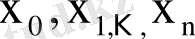 берілген, және осы нүктелердегі кейбір
берілген, және осы нүктелердегі кейбір
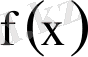 функциясының мәні
функциясының мәні
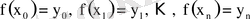 .
.
Берілген функция үшін интерполяция түйіндерінде
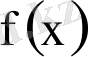 мәндерін қабылдайтын
мәндерін қабылдайтын
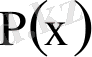 көпмүшесі тұрғызылады, яғни
көпмүшесі тұрғызылады, яғни
.
Сонымен бірге
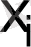 мәндерінің арасында бірдей мәндер жоқ деп есептеледі,
мәндерінің арасында бірдей мәндер жоқ деп есептеледі,
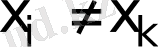 ,
,
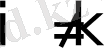 . Яғни, интерполяциялық көпмүше бастапқы функцияға жақын болу үшін берілген нүктелер жүйесінде олардың мәндері дәл келеді.
. Яғни, интерполяциялық көпмүше бастапқы функцияға жақын болу үшін берілген нүктелер жүйесінде олардың мәндері дәл келеді.
Егер интерполяциялық көпмүшенің дәрежесі
 -ге тең болса, онда глобалді интерполяция деп айтады (
-ге тең болса, онда глобалді интерполяция деп айтады (
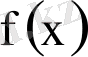 функциясын интеполяциялауда
функциясын интеполяциялауда
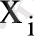 аргументінің өзгеру интервалында бір ғана көпмүше қолданылады) . Интерпоялциялық көпмүшелерді
аргументінің өзгеру интервалында бір ғана көпмүше қолданылады) . Интерпоялциялық көпмүшелерді
 аргументінің өзгеру интервалының әртүрлі бөліктерінде тұрғызуға болады. Мұндай жағдайларды үзікті интерполяция (кусочная интерполяция) деп атайды.
аргументінің өзгеру интервалының әртүрлі бөліктерінде тұрғызуға болады. Мұндай жағдайларды үзікті интерполяция (кусочная интерполяция) деп атайды.
Интерполяциялаудың негізгі шарты бойынша интерполяциялық көпмүше графигі интеполяциялық түйіндерде функцияның берілген мәндері арқылы өту керек.
Есептің қойылымы. Жуық көпмүшелерді құру әдістерінің біреуі ретінде төмендегі есепті қарастыратын интерполяции әдісін алуға болады.
Айталық, функция у = ƒ( х ) кестелік түрде берілген болсын:
Дәрежесі
n
-нен артпайтын, мәндері
х
к
,
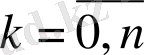 нүктелерінде берілген функция мәндерімен дәл келетін
L
n
(x)
көпмүшесін табу керек, яғни
нүктелерінде берілген функция мәндерімен дәл келетін
L
n
(x)
көпмүшесін табу керек, яғни
х
k
,
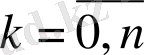 нүктелерін
интерполяциялау түйіндері
, ал
L
n
(x) -
ті
х
0,
х
1, …,
х
n
. түйіндері бойынша
ƒ(х)
функциясы үшін
интерполяциялық көпмүше
деп атайды.
нүктелерін
интерполяциялау түйіндері
, ал
L
n
(x) -
ті
х
0,
х
1, …,
х
n
. түйіндері бойынша
ƒ(х)
функциясы үшін
интерполяциялық көпмүше
деп атайды.
Интерполяиялық көпмүшелер. Интерполяциялау есептерін шешу Лагранж интерполяциялық көпмүшесі болады.
ƒ(х) функциясын интерполяциялау үшін интерполяция түйіндерінде берілген функция өзінің интерполяциялық көпмүшесімен сәйкес болу қажеттілігі есептің қойылымында беріледі. Егер х интерполяциялау түйіні болмаған жағдайда ƒ(х) функциясы L n (x) - көпмүшесіне жуық тең болады, демек
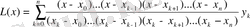
r n (x) арқылы ƒ(х) - L n (x) айырымын белгілеп алу арқылы келесі теңдікті жазуға болады:
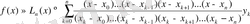
Бұл теңдік Лагранжа интерполяциялық көпмүшесі , ал r n (x) - қалдық мүше деп аталады.
f(x) функциясына және х 0 , х 1 , …, х N түйіндеріне сәйкес келетін сплайн (интерполяциялық текше сплайн) деп, келесі шарттарды қанағаттандыратын S(x) функциясы аталады:
1) Әрбір [x i-1 , x i ], i=1, 2, …, N сегментінде S(x) функциясы үшінші дәрежеләі көпмүше болады.
2) S(x) функциясы және оның бірінші, екінші туындылары [а, b] аралығында үзіліссіз;
3) интерполяциялау шарты: S(x i ) =f(x. i ), i=0, 1, …, N.
Аталған шарттарды қанағаттандыратын сплайн жалғыз ғана болатынын дәлелдейміз және оны тұрғызуды көрсетеміз.
Әрбір [х i-1, . х i ], i=1, 2, . . . , N аралықта төмендегі түрдегі S(x) =S i (x) -ті іздейміз
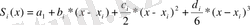
мұнда a i , b i , c i , d i - коэффициенттер. Барлығы 4N коэффициенттер, туындыны табамыз.
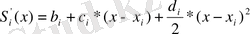 ;
;
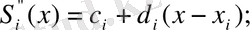
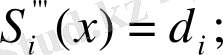
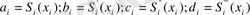
Интерполяциялау шарты бойынша S(x i ) =f(x i ), i=1, 2, . . . , N аламыз, және a I =f(x i ), i=1, 2, . . . , N, сонымен қатар, а 0 =f(х 0 ) . Осындай түрде а i , i=1, 2, . . . , N үшін N коэффициенттерді анықтайды .
Бұдан әрі S(x) функциясының үзіліссіздігінен S(x) =S i (х), i=1, 2, . . . , N шығады. Осыдан (10. 1) -ді ескере отырып, i=0, 1, . . . , N-1 үшін теңдеулер аламыз
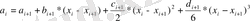
h i =x i -x i+ 1 -белгілеп аламыз, онда бұл теңдеулер a i =f(x i ) =f i -ді еске алумен бұл теңдеулерді келесі түрде жазуға болады:
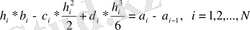
Бірінші туындының
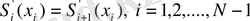 үзіліссіз шарты төмендегі теңдеуді шығарады:
үзіліссіз шарты төмендегі теңдеуді шығарады:
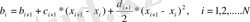
Бұрынғы қабылданған белгілеулерді ескере отырып бұл теңдеулерді келесідей жазуға болады:
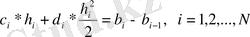
Екінші туындының
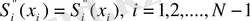 үзіліссіз шартынан келесі теңдеуді аламыз:
үзіліссіз шартынан келесі теңдеуді аламыз:
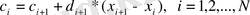
Оларды мына түрде жазуға болады:
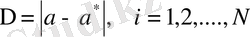
(10. 2 ), (10. 3) , (10. 4) формулаларын біріктіре отырып, 3N болатын b i , c i , d i , i=1, 2, . . . , N . белісіздерге байланысты 3N-2 теңдеулер жүйесін аламыз.
Жетіспейтін екі теңдеуді алу үшін
S(x)
-ке шеттік шарттар береміз
.
Мысалы,
f(x)
-функциясы
(a) =0 (b) =0
шарттарын қанағаттандыратын болсын
.
Бұл жағдайда
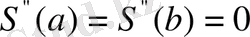 болуына талап қоюға болады. Осыдан
болуына талап қоюға болады. Осыдан
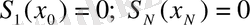 аламыз.
аламыз.
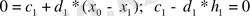 немесе
немесе
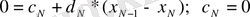
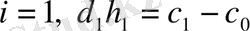 үшін (8. 4) жазып аламыз және алынған
үшін (8. 4) жазып аламыз және алынған
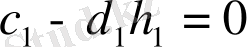 салыстырып, егер
салыстырып, егер
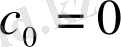 болса олардың сәйкес болатынын көреміз.
болса олардың сәйкес болатынын көреміз.
Демек, текше сплайн коэффициенттерін анықтау үшін тұйық теңдеулер жүйесіне келеміз.
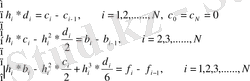
Енді, жүйенің жалғыз шешімі болатынына көз жеткізейік. (10. 5) -(10. 7) -тен b i , d i , i=1, 2, . . . , N-1 айнымалыларын шығару нәтижесінде с i , i=1, 2, . . . , N-1 -терден тұратын жүйені аламыз. Ол үшін (10. 7) көрші теңдеулерін қарастырамыз:
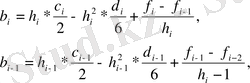
және бірінші теңдеуден екінші теңдеуді аламыз.
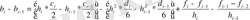
Пайда болған b i -b i-1 өрнектерін (8. 6) теңдеуінің оң жағына қою арқылы төменгі формуланы аламыз:
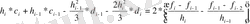
Бұдан әрі (10. 5) теңдеуінен, оны
h
i
және
h
i-1
-ке көбейтеміз:
i
үшін
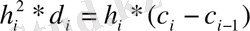 ;
i-1
үшін
;
i-1
үшін
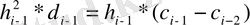 .
Бұл өрнектерді (10. 8) -ге қоямыз:
.
Бұл өрнектерді (10. 8) -ге қоямыз:
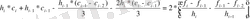
осыдан
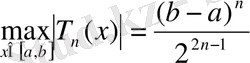 . Демек,
c
i
коэффициенттерін анықтау үшін келесі теңдеулер жүйесін аламыз:
. Демек,
c
i
коэффициенттерін анықтау үшін келесі теңдеулер жүйесін аламыз:

Осы жүйенің матрицасын жазайық:

Бұл матрицада диагоналдық элементтердің осы жолдағы диагоналға жатпайтын элементтерден көбірек екенін байқауға болады. Осындай матрицалы жүйеде тек қана бір шешім болады. Сонымен қатар, жүйе матрицасы үшКроме того, так как матрица системы диагоналді болғандықтан оның шешімін ее решение легко найти методом қумалық әдіс арқылы шешуге болады(метод прогонки) .
Табылған c i коэффициенттері бойынша b i және d i коэффициенттері (10. 5) және (10. 7) формулаларынан алынған формулалар көмегімен бұрынғыдай анықталады:
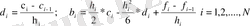
Шеттік шарттар ретінде басқа шарттарды қарастыруға болатынын және, қарастырған жағдайда бұл шарттар ретінде
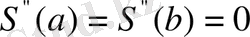 алынғанын ескертеміз.
алынғанын ескертеміз.
Ньютонның интерполяциялық формуласы
Айталық у = ƒ( х ) функциясы кестелк түрде берілсін:
Дәрежесі
n
-нен аспайтын,
х
к
,
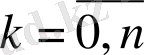 нүктелеріндегі мәндері берілген функцияның мәндерімен сәйкес болатын
L
n
(x)
көпмүшесін табу қажет болсын. Қойылған есептің шешімі к өпмүше
Р
n
(x) ≡L
n
(x)
болады:
нүктелеріндегі мәндері берілген функцияның мәндерімен сәйкес болатын
L
n
(x)
көпмүшесін табу қажет болсын. Қойылған есептің шешімі к өпмүше
Р
n
(x) ≡L
n
(x)
болады:
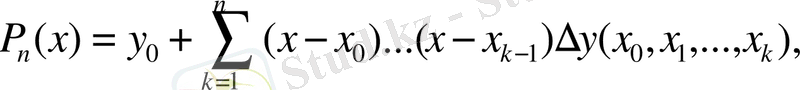
мұнда ∆y (х 0, х 1 ), ∆y(х 0, х 1, х 2 ), …, ∆y(х 0, х 1, …, х n ) - төмендегі формулалар арқылы есептелетін айырымдық қатынастар:
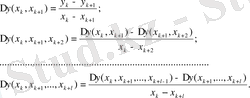
Мұндай көпмүшені Ньютонның интерполяциялық көпмүшесі деп, ал
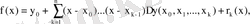
формуласын Ньютонның интерполяциялық формуласы деп атайды.
Ньютона формуласының Лагранж формуласынан артықшылығы, егер алынған интерполяция түйіндеріне тағыда бір түйін қосса Лагранж формуласының барлық мүшелері өзгеріп, сандары үлкейеді, ал Ньютон формуласындағы барлық табылған мүшелер сақталады және жаңа қосындылар қосылып отырады. Дегенмен, Лагранж формуласы басқа жағдайларда ыңғайлы: мысалы, интерполяциялау түйіндерінің бір жүйесінде бірнеше функцияларды интерполяциялау қажет болса. Әдетте айырымдық қатынастарды 1 -кестесі түрінде жазып алады (анықтылық үшін n= 4 деп аламыз) . Ньютон интерполяциялық формуласына 1- кестеде көрсетілген айырымдық қатынастар кіреді (бұл айырымдық қатынастардың асты сызылған) .
Тең қашықтықта орналасқан х k = х 0 + kh, k=0, n түйіндер үшін h >0 интерполяциялау қадамымен Ньютон көпмүшесі келесі түрде болады:
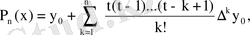
мұнда t=(x - х 0 ) / h, а ∆ k y 0 - k- ші ретті шеттік айырымдар.
Шеттік айырымдарды есептеу үшін 2-кестесін құрамыз (анықтылық үшін n = 4 деп аламыз) .
1-кесте
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz