8-сыныпта экстремумге берілген есептерді алгебралық әдістермен шешу


8-сыныпта алгебраны оқыту барысында экстремумға берілген есептерді шешу әдістері
Бізді қоршаған ортадағы табиғат құбылыстарына байланысты есептерді, экономикалық есептер мен механиканың есептерін, математикалық программалау мен тиімділік есептерін шығару математикалық тұрғыдан белгілі бір теңдеулер, теңсіздіктер немесе теңдеулер мен теңсіздіктер жүйесін шешуге әкеледі. Ендеше осы есептерді шешу тәсілдерін, соның ішінде тиімді тәсілдерін іздестіру әруақытта күн тәртібінен түскен емес. Есептердің жататын тобына байланысты оларды шығару тәсілі де әр түрлі болып келеді. Тиімділік есептерін, «экстремумға» берілген есептерді шығару дифференциалдық есептеулерді, ал аудан, көлем табу, жылу өткізгіштік т. с. с. есептерді шығару интегралдық есептеулерді қолдану арқылы шығарылады.
Солай бола тұрса да, мұндай есептердің шығарудың басқа алгебралық, геометриялық тәсілдері де бар. Олар тіпті дифференциалдық және интегралдық есептеулер ашылмастан да бұрын қолданылған әдістер. Кейбір жеке жағдайларда мұндай әдістер дифференциалдық және интегралдық есептеулерден де тиімдірек екені практикада байқалып жүрген жағдай. Есепке әртүрлі жолмен келуді көрсету әруақытта ұтымды. Әртүрлі тәсілдермен шығарылатын есептер барлық уақытта қызықты және белгілі бір тұжырым жасауға ыңғайлы. Есептерді шығарудың әртүрлі тәсілдерін өзара салыстыру арқылы оқушыларда есепті шығару жолын іздестіру жүйесі қалыптасып, интуицияларының дамуына мүмкіндік туып, қажетті тәжірибелер жинақталады.
Ең үлкен және ең кіші мәндерді табуға арналған есептерді қарапайым математика әдістерімен шешуге болады. Онда квадраттық функция қолданылады.
Есептерді осы әдіспен шығарғанда өткен дәрісте дәлелденген төмендегі теоремаға сүйенеміз:
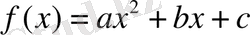 квадраттық функциясы
квадраттық функциясы
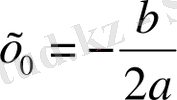 нүктесінде
нүктесінде
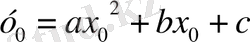 экстремальды мәнін қабылдайды. Ол a <0 болса максимум (ең үлкен мәні), a > 0 минимум (ең кіші мәні) болады.
экстремальды мәнін қабылдайды. Ол a <0 болса максимум (ең үлкен мәні), a > 0 минимум (ең кіші мәні) болады.
Мысал келтірейік.
Есеп. Қолда бар тақталардан ұзындығы 200 метр шарбақ тұрғызуға болады. Ең үлкен аумақтың төртбұрышты ауласын бір жағына бұрыннан салынған қабырғаны пайдаланып, осы дуалмен қоршау қажет.
Қоршаудың екі жағының ұзындығы х, ал қабырғаға параллель жатқан қабырғасының ұзындығы у болсын. Сонда есептің шарты бойынша 2x+y=200, y=200-2x, y=2(100-x) өрнектейміз. Ауланың ауданын S арқылы белгілеп, S=xy, S(x) =2x(100-x) .
Функцияның графигі тармақтары төмен бағытталған парабола болғандықтан және олар абсцисса осін 0 және 100 нүктелерінде қиып өтетіндіктен, параболаның төбесі осы осьтегі 50 санына сәйкес келеді.
Жауабы: Қоршаудың қабырғаларының ұзындығы 50м, 100м және 50м.
Алгебра курсындағы экстремалды есептерді шешу екі кезеңде жүзеге асырылады. Бірінші кезеңде анықталмаған (белгісіз) есеп қарастырылады, оның мәтіні математикалық тілге анықталмаған (белгісіз) теңдеу немесе функция) түрінде аударылады. Бұл көптеген немесе шексіз көп шешімдер алуға мүмкіндік береді
Екінші кезеңде нақты немесе жасырын түрде берілген бір белгілерге сәйкес есептің қай шешімі ең тиімді екендігі анықталады.
Берілген кесіндідегі сызықтық фунуциясының экстремумының мәндерін табу
y = kx+l (мұндағы x - тәуелсіз айнымалы, k мен l - нақты сандар) түріндегі формуламен берілетін фуннкцияны сызықтық функция деп атайды.
Берілген кесіндіде үзіліссіз функциясы берілді делік, және оның санаулы күдікті нүктелері болсын. Функцияның кесіндісінде бірнеше үлкен мәндері болса, онда ол экстремумдардың біреуі функцияның ең үлкен мәні болып табылады, атап айтқанда табылған нүктелердегі функциялардың ең үлкен мәні болып табылады.
Сонымен, функциясының ең үлкен мәні кесіндісінің ұштарында, немесе осы кесіндідегі максимум нүктесінде болады.
Мұндай есептердің бар болуы математиканың өмірге аса қажетті пән екенін дәлелдейді. Көптеген мәселелер, функцияның экстремумын табуға әкеледі. Мысалға экономиялық есептер, немесе қарапайым мәтіндік есептер.
Сызықтық функция мектеп қабырғасында алтыншы сыныптан бастап қарастырылған, құрылымы күрделі емес болғандықтан оқушыларға көп киындық түсіре бермейді. Курстың бастамасы берілген функцияның гиафигін салудан бастап, соңында қолданбалы есептерді шешуге тапсырмалар беріледі, ал көпдеген қолданбалы есепетрді шығару барысында бізге экстремумдарының мәндерін табу керек болады. Сондықтан ең қарапайым сызықтық функциянының ерекшеліктері мен оны нақты өмірмен байланыстырып түсініу және қолдану өте маңызды деп есептеймін.
Сызықтық функция не шексіз өспеді немесе шексіз кемімелі болып табылады, сондықтан оның экстремумдары жоқ. Бірақ егер оған белгілі шектеулер қойсақ, онда оның сол аралықтағы экстремумының мәндерін анықтай аламыз. Сол себепті мектеп бағдарламасында: “берілген кесіндідегі сызықтық фунуциясының экстремумының мәндерін табуға арналған есептер” болып кездеседі.
Квадраттық функцияның экстремум мәндерін табу
Квадраттық функция деп мына түрде беруге болатын функцияны айтады . Квадраттық функцияның графигі парабола деп аталады. Жалпы түрде квадраттық функцияның теңдеуі мына түрде жазылады: . Парабола төбесінің координаттары:( , . түзуі квадраттық функция графигінің симметрия осі деп аталады. Егер a<0 болса парабола төмен тармақталған болады, a>0 болғанда - жоғары тармақталған.
Көптеген есептерде квадраттық функцияның максималды немесе минималды мәнін есептеу керек болады. Егер бастапқы функция стандартты түрде жазылса, максимум немесе минимумды табуға болады:
немесе параболаның жоғарғы координаталары арқылы: . Cонымен қатар, кез-келген квадраттық функцияның максимумын немесе минимумын математикалық операциялар арқылы табуға болады.
Бірінші әдісін қарастырайық. Квадраттық функция стандартты түрде жазылсын:
I есептеу. Параболаның бағытын анықтаңыз.
Квадраттық функцияның графигі параболаны білдіреді. Параболаның тармақтары жоғары немесе төмен бағытталған. Егер а коэффициенті оң болса, парабола жоғарыға бағытталған. Егер а коэффициенті теріс болса, парабола төменге бағытталған. Мысалы:
. Бұл жерде а=2, сондықтан параболаның тармақтары жоғарыға бағытталған.
. Бұл жерде а=-3, сондықтан парабола тармақтары төменге бағытталған.
. Бұл жерде а=1, сондықтан парабола тармақтары жоғары тармақталған.
Егер параболаның тармақтары жоғарыға бағытталған болса, оның минимумын табу керек. Егер төменге бағытталса, керісінше максимумын табу керек болады. Біздің жағдайымызда а=2, жоғары бағытталған, сондықтан минимумын табу керекпіз.
II есептеу. -ны есептеу қажет.
мәні парабола төбесі. Егер квадраттық функция стандарт түрінде жазылған болса, онда және х коэффициенттерін төмендегідей қолданыңыз:
функцияның коэффициенттері a=1 және b=10 болады. Параболаның төбесі х-ты былай есептейміз:
Мысал ретінде функциясын қарастырайық. Бұл жерде
a=-3 және b=6. Сондықтан параболаның төбесі х-ты былай есептейміз:
III есептеу. -тың сәйкес мәндерін табу. Табылған х мәнін берілген функцияға қойып, -тың сәйкес мәндерін табу қажет. Осылай функцияның максимум немесе минимум мәндерін табамыз. Бірінші мысалда
біз х=-5 - ке тең екенін тапқан болатынбыз. Енді бұл мәнді функцияға апарып қойып, функцияның максимум мәнін табамыз:
.
Екінші мысалда бізде х=1-ге тең болды. Осы тапқан мәнді функцияға апарып қойсақ, функцияның максимум мәнін табамыз:
.
Жауабы:бірінші мысалда парабола төбесінің координатасы (-5, 26) және функцияның минимум мәні -26. Екінші мысалда, парабола төбесінің координатасы (1, -1), максимум мәні -1.
Қолданбалы есептерге мысалдар келтіретін болсақ:
1-мысал. Периметрі 40 см болатын тіктөртбұрыштың ауданы ең үлкен мән қабылдау үшін, тіктөртбұрыштың қабырғалары қандай болуы керек?
P=2(a+b)
2(a+b) =40
a+b=20
b=20-a
S=a b= a (20-a) - ең үлкен мән
a=-1<0
a= =10
b=20-10=10
S= a b= 10 10=100
Жауабы: 10
2-мысал. Әлібек 42 m темірмен үйдің бір қабырғасына жалғап тіктөртбұрыш тәізді қоршау жасамақ болды, үйдің осы қабырғасы 18m ге тең, яғни қоршаудың ұзындығы 16m ден аспауы қажет, ені неше метрге тең болғанда, қоршаудың ауданы ең үлкен болады? Ең үлкен мәні неше?
Шешуі : Қоршаудың енін xm деп алсақ, онда ұзындығы (42-2x) ке тең.
S=x
S=
X= (m), (
Жауабы:10, 5 m; 220, 5 .
3-мысал. Құрылыста ұзындығы 167 м болатын су құбырын жүргізу керек. Ұзындықтары 5м және 7м болатын құбырлар бар. Жалғаулар саны аз болатындай етіп құбырларды кеспестен 5м-лік немесе 7м-лік құбырлардың қаншауын қолдану қажет .
Шешуі:
5м-лік құбырлардың санын у, ал 7м-лік құбырларды х деп белгілейміз. Сонда 7х-7м-лік құбырдың ұзындығы, 5у-5м-лік құбырдың ұзындығы. Осыдан келесі теңдеуді аламыз:
7х+5у=167
у-ті х арқылы өрнектесек:
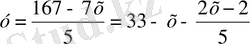 .
.
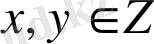 болғандықтан, 7х+5у=167 теңдеуін қанағаттандыратын х пен у-тің мәндерін іріктеу арқылы алсақ болады:. (1; 32), (6; 25), (11, 18), (16; 11), (21; 4) . Бұл шешімдердің ішінен ең тиімдісі соңғы шешім, яғни: x=21, y=4.
болғандықтан, 7х+5у=167 теңдеуін қанағаттандыратын х пен у-тің мәндерін іріктеу арқылы алсақ болады:. (1; 32), (6; 25), (11, 18), (16; 11), (21; 4) . Бұл шешімдердің ішінен ең тиімдісі соңғы шешім, яғни: x=21, y=4.
Жауабы: Жалғаулар саны аз болатындай етіп құбырларды кеспестен 21 7м-лік құбыр 45м-лік құбырларды қолдану қажет.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz