Математикадан экстремумге берілген қолданбалы есептерді шешу әдістемесі

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 25 бет
Таңдаулыға:

Математикадан экстремумге берілген қолданбалы есептерді шешу әдістемесі
1-курс, 2-семестр, 2021-2022 оқу жылы
7М01501-Математика ММОК-211-214
Құрастырған: Б. Қасқатаева
Практикалық сабақтар.
1- практикалық сабақ
Экстремумге берілген қолданбалы есептер туралы жалпы мәліметтер және оның даму тарихы
Экстремумға берілген есептер, олардың түрлері және ондай есептерді шешудің тиімді әдістері жайлы сөз қозғамас бұрын экстремум, максимум, минимум ұғымдарының мән-мағынасына тоқталайық.
Қазақ сөздігі деп аталатын Қазақ тілінің біртомдық үлкен түсіндірме сөздігінде Экстремум (лат. еxtremum) функцияның математикалық ең көп және ең аз мәндері деген анықтама берілген [16]. Сондай-ақ орта мектептің 11 сыныбына арналған Алгебра және анализ бастамалары оқулығында экстремум сөзі латынша Extremum (шеткі) дегеннен келіп шыққанын айта кетіп, қазақша maximum-ең үлкен, minimum-ең кіші деп аударылды делінген [17]. Ал интернет желісінде бұл сөзге экстремум -математикада берілген аралықтағы функцияның ең үлкен немесе ең кіші мәні деп анықтама берілген. В.М.Тихомировтың Рассказы о максимумах и минимумах атты кітабында, экстремум сөзі шеткі деген мағынаны білдіретіні және ол максимум мен мининум түсініктерінің бірігуі деп анықтама береді[11].
Экстремум сөзі аталған кезде максимум және минимум сөздері де онымен бірге ажырамай айтылады. Ол сөздер де күрделі ұғымдар болып табылады және түрлі әдебиеттерде әралуан анықтамалар беріледі. Себебі біз бұл сөздерді тек математикада ғана емес, тұрмыста да көптеп кездестіреміз. Енді бірінші бұл сөздің тұрмыста қолданылатын анықтамасына тоқталып өтсек:
Орысша қазақша сөздікте максимум сөзіне ең үлкен, ең көп, қандай да бір заттың мүмкін болатын ең үлкен мөлшері, баға жағынан: ең қымбат баға, бір нәрсенің шектік мөлшері, ең жоғарғы дәреже т.с.с. анықтамалар берілген.
Ал минимум сөзі ең кіші шама, ең кіші, ең аз, бір нәрсенің берілген жағдайдағы ең аз мөлшері деген мағыналарды білдіреді.
1. Қазақстан ұлттық энциклопедиясында Минимум (лат. minimum-ең кіші), функцияның минимумы, функцияның ең кіші мәні - берілген Е жиынындағы функциясының ең кіші мәні; түрінде белгіленеді.
Максимум (лат. maximum-ең үлкен) функцияның максимумы, функцияның ең үлкен мәні - берілген Е жиынындағы 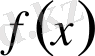функциясының ең үлкен мәні; 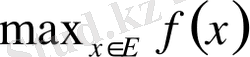түрінде белгіленеді деп атап өтілген[18].
А.Е.Әбілқасымова, К.Д.Шойынбеков, В.Е.Корчевский, З.А.Жұмағұлованың авторлығымен шыққан 10-сынып Алгебра және анализ бастамалары атты оқулығында максимум және минимум ұғымдарына төмендегідей анықтама берілген:
Анықтама. Егер 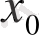нүктесінің қандай да бір аймағынан алынған барлық x (мұндағы 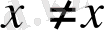үшін 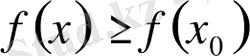теңсіздігі орындалса, онда 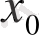нүктесі 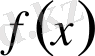функциясының минимум, ал 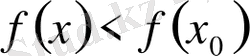теңсіздігі орындалса, максимум нүктесі деп аталады.
Максимум және минимум нүктелерін экстремум нүктелері деп атайды. Функцияның осы нүктелердегі мәндерін функцияның экстремумы деп атайды деп атап көрсетілген [19].
Экстремумға берілген есеп ұғымына түсініктеме беретін болсақ, ол максимум немесе минимумын табуға арналған есеп деген мағынаны білдіреді. Математика саласында экстремумдарды (максимум және минимумдарды) зерттеу өте ертеден, жиырма бес ғасыр бұрын басталған. Ұзақ уақыт бойы бұл мәселе өз шешімін таба қоймаған еді, дегенмен үш жүз жыл бұрын заман жаңалығы болып алғаш математикалық талдау салаларына ене бастаған. Неге бұл тақырыпқа деген қызығушылық соншалықты күшті болды? Оның атап айтарлық бірнеше себептері бар. Біріншіден, максимум және минимумға берілген есептердің ішінде тамаша, қызықты және шығаруға жағымды есептер өте көп. Бірақ адамдар ондай есептерді тек жақсы көргендіктен шығарып қана қойған жоқ, ондай есептер ғалымдардың үстелінде өмірде қолданысқа қажет болғаны үшін, практикада кездескені үшін де жатты. Максимумдар мен минимумдар инженерлік салада, архитектурада, экономика саласында әрдайым қолданыста болды. Сонымен қатар, экстремумға берілген есептер күтпеген жерден табиғат туралы ғылымдарда, яғни физика, химия, биология салаларында да қажет бола бастады. Қарап отырсақ, қоршаған орта экстремумдық заңдар негізінде құрылғанын байқаймыз. Экстремумға берілген есептер әр түрлі тақырыптарда геометрияда, алгебрада, математикада да кездеседі. Мысалы, 0,1,2,3,4,5,6 және 7 цифрларының барлығымен жазылатын және цифрлар қайта қайталанбайтын:
1) ең үлкен санды жазыңдар;
2) ең кіші санды жазыңдар.
Шешуі: Ең үлкен натурал сан: 76543210
Ең кіші натурал сан: 10234567. Бұл 5-сынып математика оқулығында кездесетін қарапайым ғана экстремумға берілген есеп болып табылады [20].
Оқушыларға бұл тақырыпты үйрету барысында максимум нүкте, минимум нүкте мен функцияның максимум мәні және минимум мәні деген түсініктердің бір-бірінен үлкен айырмашылық жасайтынына тереңірек тоқталып өту керек. Максимум және минимум нүктені біз абсцисса осінің бойынан іздесек, максимум және минимум мәндерді біз сол нүктелерге сәйкес Оу осінің бойынан, яғни ординаталар осінен іздейміз. Тағы да көпшілік балаларда ең үлкен мән мен ең кіші мәнді осы максимум және минимуммен шатастыру қателігі өте басым, себебі олар бұл ұғымдардың айырмашылығын терең түсіне бермейді, екеуі бір ұғым деген өздеріне түсінік қалыптастырып алған. Ал шындығына келгенде бұл ұғымдарда үлкен айырмашылықтар бар. Функцияда ең кіші (ең үлкен мән) мән біреу ғана болады, ал минимум (максимум) нүктелер көп болуы мүмкін.
Экстремумға берілген есептер әлі күнге дейін бір жүйеге келтірілмеген, ондай есептерді шығарудың әдістемесі жасалып, бір ізге түсірілмеген. Қазіргі таңда экстремумға берілген есептермен мектеп оқушылары тек 10-11 сыныптарда туынды тақырыбын өту кезінде ғана танысады.
Экстремумға берілген көп есептер туындының көмегімен шығарылады, алайда оларды элементар әдістермен де шығаруға болады. Ондай әдістермен негізгі мектеп оқушыларын таныстырып, есептер шығарып жаттықтыратын болсақ, оқушылар жоғары сыныптарда өтілетін экстремум ұғымымен ертерек танысып, жоғары сыныпта ол тақырыпты өту барысында еш қиындықсыз оңай меңгеруіне және де күнделікті өмірде кездесетін экстремумға берілген есептерді шығара алуына үлкен көмек болар еді.

2- практикалық сабақ.
Оқушылардың математикалық сауаттылығын дамыту мақсатында экстремумге берілген қолданбалы есептерді шешу.
Есеп. Балаларға арнап сыйлық алынды. 12 қалың дәптер, 16 қаламсап және 8 түрлі түсті карандаш. Әр сыйлықтағы қалың дәптер, қаламсап және түрлі түсті карандаштардың саны бірдей болса, ең көп дегенде неше сыйлық әзірлеуге болады?
Шешуі: ЕҮОБ(12,16,8)=4. Демек, 4 сыйлық дайындауға болады [35].
Диаграммалар тақырыбы жаңартылған мазмұндағы бағдарлама бойынша 5-сынып математика курсына енгізілді. Ол тақырыпта статистикалық мәліметтерді көрнекі түрде диаграммалар арқылы кескіндеу көрсетілген және ол жерде де экстремумға берілген қарапайым тапсырмаларды кездестіруге болады.
13-есеп. 26-суретте Меркурий, Шолпан, Жер және Марс ғаламшарларының радиустарын көрсететін бағанды диаграмма сызылған. Бағанды диаграмма бойынша онда берілген ғаламшарлардың ең үлкені қайсысы? Ең кішісі қайсысы?

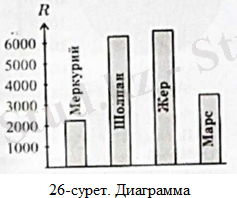
Шешуі: Диаграммадан көріп тұрғанымыздай ең үлкені - Жер, ең кішісі - Меркурий [36].
Біз жоғарыда 5-сынып мектеп математика курсында кездесетін экстремумға берілген тапсырмалардың біразына тоқталып өттік, енді 6-сынып математика курсындағы оқулықтарға талдау жасау арқылы экстремумға берілген есептерге шолу жасаймыз.
Нақты процестердің графиктерін пайдаланып, шамалар арасындағы тәуелділіктерді зерттеу тақырыбында 6-сынып 2018 жылы жаңартылған мазмұндағы білім беру бағдарламасына сәйкес шығарылған математика оқулығында кездесетін кейбір есептерге тоқталып өтейік.
14-есеп. 27-суретте 21 наурыз күні соққан желдің жылдамдығының тәулік бойындағы өзгеріс графигі кескінделген.
График бойынша анықтаңдар:
1) Желдің ең жоғарғы жылдамдығын
2) Қай уақыт аралығында желдің жылдамдығы жоғары болды?
3) Қай уақыт аралығында желсіз ауа - райы байқалды?

Шешуі: 1) Желдің ең үлкен жылдамдығы 5мс болды;
2) Сағат 14-тен 20-ға дейін желдің жылдамдығы 5мс болды;
3) Сағат 6-дан 8-ге дейін және 22-де.

3-4 практикалық сабақ
5-6 сыныптардың математика курсында экстремумге берілген қолданбалы есептерді шешу әдістері

2-мысал. Шойыннан жасалған құйманың массасы 16 кг. Әрқайсысының массасы 12 кг болатын 41 деталь жасау үшін қанша шойын құймасы қажет болады?
Шешуі: Бірінші әдіс. 1 детальдың массасы 12 кг болғандықтан, алдымен 41 детальдың жалпы массасын есептеп аламыз. Ол 41·12=492 кг - ға тең екен. Енді 1 шойын қоймасы 16 кг болатын болса 492:16=30 (қалдық 12) 41 детальға 31 шойын құймасы керек болады. Қалдығы көп не аз екендігі маңызды емес. Ал балалар қалдығына мүлде мән бермей 30 шойын құймасы керек деп қате тұжырым жасайды.
Екінші әдіс. n - құймалардың саны болсын, онда 16n - құймалардың массасы, ал 12·41 - детальдардың массасы.
Ары қарай оқушылар осы берілгендер арқылы есеп шартына сәйкес мынадай теңсіздік құрады:
16n12·41
16n492
n 492:16
n 30. Осыдан N - нің мәндері мына шексіз жиынды құрайды:

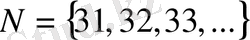
Шойын құймаларының ең аз шамасы 31 болады.
5-6 сынып оқушыларын экстремумға берілген есептерге қызықтыру үшін оларға өмірмен байланысты экономикалық мазмұндағы есептер берілсе, олар өте қызығушылықпен шығарады. Сондай есептердің бірін мысал ретінде көрсететін болсақ:
3-мысал. Қала халқын қамтамасыз ету үшін 4 ауылдан 3000т картоп сатып алу керек. Әр ауылдан алуға болатын картоп мөлшері мен 1т картопты тасу құны төмендегі 1-кестеде көрсетілген:

1-кесте

Әр ауылдан алуға болатын картоптың мөлшері мен 1т картопты тасу құны

Картоптың мөлшері (тоннамен)
1100
900
800
700
1т картоптың бағасы (рубльмен)
3
2,5
2
2,7

Картопты тасу құны ең аз болатындай етіп қаланы картоппен қамтамасыз ететін жоспар құру керек.
1 - кестеден көріп тұрғанымыздай, егер 1 т картопты тасу құнының арзандығы бойыша орналастыратын болсақ: 2; 2,5; 2,7; 3 деп орналасады, ал оларға сәйкес картоп мөлшері мына ретпен тұрады: 800; 900; 700; 1100.
Есептің шешімі бағалау әдісімен табылады:
1. 8003000
2. 800+900=17003000
3. 1700+700=24003000
4. 2400+11003000
5. 3000-2400=600
6. 800·2+900·2,5+700·2,7+600·3=7540 руб.
Демек, қалаға әкелінетін картоптың ең аз, тиімді бағасы 7540 рублді құрайды [6, 8-10].
Тіктөртбұрыштың ауданы және периметрі тарауында оқушыларға мынадай есеп беруге болады. Ауданы 36 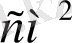болатын тіктөртбұрыш сызыңыз.
Оқушылардың шығармашылық қабілетін арттыру үшін тіктөртбұрыштың периметрі ең кіші болуы туралы ешқандай сұрақ қоймаймыз, сонда бала өзі шешімге келеді. Ауданы 36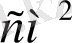болатын тіктөртбұрыштардың өлшемдері әр түрлі болуы мүмкін, оқушы соларды салыстыру арқылы өзі бір шешімге келеді. Тіктөртбұрыштың мүмкін өлшемдерін кестеде көрсетейік.
Тіктөртбұрыштың мүмкін өлшемдері

Аудан
36
36
36
36
36
36
36
Ұзындық
72
36
18
12
9
8
6
Ені
(12)
1
2
3
4
412
6
Периметр
145
74
40
30
26
25
24

Кестедегі өлшемдерді салыстыра отырып оқушы аудандары бірдей тіктөртбұрыштардың ішінде ең кіші периметр квадраттың периметрі болатынына өзі көз жеткізеді. Немесе есепті керісінше беруге болады. Периметрі бірдей тіктөртбұрыш сызу берілсін, мысалы периметрі 20см болуы керек. Мұнда да ауданы ең үлкені жайлы ештеңе айтпаймыз, оқушы есепті шығару барысында өзі көз жеткізіп, периметрлері бірдей тіктөртбұрыштарды зерттеу арқылы өзі бір ерекшелікті байқап бір қорытындыға келуі керек. Тағы да тіктөртбұрыштың мүмкін өлшемдерін келесі кестеде көрсетейік:

Тіктөртбұрыштың мүмкін өлшемдері

Периметр
20
20
20
20
20
Ұзындық
9
8
7
6
5
Ені
1
2
3
4
5
Аудан
9
16
21
24
25

Кестеде тек натурал сандармен ғана көрсеттік, негізі бөлшек сандарды да қолданып есептеуге болады. Кестені өзі сызып, есептеу барысында оқушы периметрлері бірдей тіктөртбұрыштардың ішінде квадраттың ауданы ең үлкені болатынына көз жеткізеді.
Үш автобус таңғы сағат 6-да бір станциядан әр түрлі бағыттарда жолға шықты. Олар сол бағытта барады және кері қайтады: бірінші автобус - 40 минут, екінші автобус - 1 сағат, ал үшінші автобус - 50 минут сайын сол станцияға қайтып келіп отырады. Ең кем дегенде қанша уақыттан кейін үш автобус дәл сол станциядан бірдей уақытта жолға шығады [6, 17].
Бұл есептің шешімі мына түрде келтіріледі. ЕКОЕ(40, 60, 50)= 600. Демек, ең аз дегенде үш автобус, сол станцияда 600 минуттан кейін, яғни 10 сағаттан кейін ғана кездесе алады
Есептер
1-есеп. 0,1,2,3,4,5,6 және 7 цифрларының барлығымен жазылатын және цифрлар қайта қайталанбайтын:
1) ең үлкен санды жазыңдар;
2) ең кіші санды жазыңдар.
Шешуі: Ең үлкен натурал сан: 76543210
Ең кіші натурал сан: 10234567
2-есеп. Жанар ең кіші екі таңбалы санға ең үлкен үш таңбалы санды бірнеше рет қосты. Қосынды ең кіші бес таңбалы санға тең болады. Жанар ең үлкен үш таңбалы санды неше рет қосты?
Шешуі: Ең кіші екі таңбалы сан - 10, ал ең үлкен үш таңбалы сан - 999. Ал ең кіші бес таңбалы сан - 10000. Демек, ең үлкен үш таңбалы сан неше рет қосылғанын білу үшін алдымен 10000-10=9990 амалын орындаймыз, сосын шыққан нәтижені 999-ға бөлеміз, яғни 9990:999=10.
Жауабы: Ең кіші бес таңбалы санды алу үшін ең үлкен үш таңбалы санды 10 рет қосу керек.
Ал Натурал сандарды салыстыру тақырыбында мынадай есептер кездеседі.
3-есеп. Ананас алмадан ауыр, өрік алмадан жеңіл. Жемістердің ең ауыры қайсысы, ең жеңілі қайсысы?
Шешуі: Есепті шешу үшін берілгендерді пайдаланып қос теңсіздік құрастырамыз: өрікалмаананас. Демек, ең ауыр жеміс - ананас, ал ең жеңіл жеміс - өрік.
4-есеп. х-тің орнына қос теңсіздік тура болатындай натурал санның ең үлкенін тауып, жазыңдар:
1) 46x50
2) 5670x5680
3) 186x190

4) 32416x40000
Шешуі: 1) х=49 2) х=5679 3) х=189 4) х=39999. Себебі, бұл есепте барлығы қатаң теңсіздікпен берілгендіктен, теңсіздік таңбасының екі жағындағы сандарды қабылдамайды.
5-есеп. 5, 0 және 3 цифрларының әрқайсысын бір рет қана пайдаланып, үш таңбалы сандарды жазыңдар. Осы сандардың ең үлкені ең кішісінен қанша артық?
Шешуі:530, 503, 305, 350. Ең үлкені - 530, ал ең кішісі - 305, ал олардың айырмасы - 225. Демек, ең үлкені ең кішісінен 225-ке артық.
Ең үлкен ортақ бөлгіш және Ең кіші ортақ еселік тақырыптарында нағыз қарапайым әдістермен шығарылатын экстремумға берілген тапсырмалардың негізі қаланады. Шығарылуы өте қарапайым болғанымен Ең үлкен ортақ бөлгіш және Ең кіші ортақ еселік тақырыптарынан күнделікті тұрмыста қолданысқа ие есептерді көптеп кездестіруге болады.
6-есеп. Балаларға сыйлық дайындау үшін 180 жаңғақ, 150 өрік және 210 кәмпит алынды. Балаларға берілетін сыйлықтардағы өріктердің саны бірдей, жаңғақтардың саны бірдей, жаңғақтардың саны бірдей, кәмпиттердің саны бірдей болу керек. Сыйлық ең көп дегенде неше балаға жетеді?
Шешуі: Сыйлық ең көп дегенде неше балаға жететінін анықтау үшін өрік, жаңғақ және кәмпиттердің ең үлкен ортақ бөлгішін табамыз: ЕҮОБ(180,150,210)=30. Демек, сыйлық ең көп дегенде 30 балаға жетеді.
7-есеп. Мұнай қоймасына мұнай тиелген үш тіркес цистерналар әкелінді. Цистерналардың біріншісінде 504т, екінші тіркесінде 288т, ал үшінші тіркесінде 648т мұнай бар. Цистерналардың барлығы мұнаймен толтырылған және цистерналардың әрқайсысындағы мұнайдың массалары бірдей.
* Әрбір цистернадағы мұнайдың ең көп мүмкін массасы неше тонна?
* Цистерналардың бірінші тіркесінде, екінші тіркесінде, үшінші тіркесінде неше цистерна бар?
Шешуі: ЕҮОБ(504,288,648)=72, демек, әрбір цистернадағы мұнайдың ең көп массасы 72 т. Сонда, цистерналардың бірінші тіркесінде 504:72=7, екінші тіркесінде 288:72=4, ал үшіншісінде 648:72=9 цистерна бар.
8-есеп. Таңертеңгі сағат 8-де элеватордан астық таситын үш машина шықты. Машиналардың біріншісі 3 сағатта, екіншісі 4 сағатта, ал үшіншісі 6 сағатта элеваторға қайтып оралыр отырады. Егер машиналар бір қалыпты жүріп тұрса, олар сағат нешеде элеваторда қайта кездеседі?
Шешуі: Бұл есепті шығару үшін үш машинаның уақыттарының ең кіші ортақ еселігін табамыз. ЕКОЕ(3,4,6) =12, демек үш машина бір мезгілде элеваторға 12 сағат өткесін қайтып оралады. Олар таңертеңгі сағат 8-де шыққан болса, кешкі 8-де олар үшеуі бірдей элеваторға келеді.
9-есеп. Марканың бағасы 45тг. Айнұрда 20 теңгелік монеталар ғана бар. Егер сатушыда қайтаратын ақша болмаса, Айнұр ең кем дегенде неше марка сатып ала алады?
Шешуі: ЕКОЕ(45,20) = 180, демек Айнұр сатушы оған ақша қайтара алмайтын болса ең кем дегенде 180 теңгеге 4 марка сатып алуы керек.
10-есеп. Маржан дүңгіршектен бағасы 80тг лотерея билеттерін немесе 60 тг маркаларды сатып алуы керек. Сатушының қайтаратын ақшасы болмаған жағдайда Маржан үйінен ең кем дегенде неше теңге алып шығуы керек?
Шешуі: ЕКОЕ(80,60) = 240, егер сатушының қайтаратын ақшасы болмай қалса, Маржан үйінен ең кем дегенде 240 тг алып шығцы керек [20].
11-есеп. Екі санның қосындысы 35-ке тең. Олардың ең кіші ортақ еселігі 60, осы сандарды табыңдар.
Шешуі: 20 және 15 [33].
12-есеп. 3,4,5,6,7,8,9 сандарының арасынан өзара жай сандар жұбын тауып, олардың ең кіші ортақ еселігін табыңдар.
Шешуі: 3 пен 7, 4 пен 7, 5 пен 9, 5 пен 7, 5 пен 6, 7 мен 9, 8 бен 9, 3 пен 8, 3 пен 4, 3 пен 5, 4 пен 5, 4 пен 9, 5 пен 8. ЕКОЕ(3,7)=21, ЕКОЕ(4,7)=28, ЕКОЕ(5,9)=45, ЕКОЕ(5,7)=35, ЕКОЕ(5,6)=30, ЕКОЕ(7,9)=63, ЕКОЕ(8,9)=72, ЕКОЕ(3,8)=24, ЕКОЕ(3,4)=12, ЕКОЕ(3,5)=15, ЕКОЕ(4,5)=20, ЕКОЕ(4,9)=36, ЕКОЕ(5,8)=40 [34].

5 практикалық сабақ.
Функцияның экстремумдарын табуға берілген практикалық мазмұнды есептер
Мысал:
Функцияның кіші мәнін табу және графигін салу.

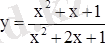
Шешуі:
Толық квадратын бөліп шығарамыз.:

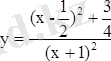
х = -1 болғанда мағнасы болмайды. Х тің басқа мәндерінде функция тек оң мән қабылдайды. Функцияның кіші мәні де оң сан болады. Оны бірден анықтау мүмкін емес. Сондықтан мынандай түрлендіру жасаймыз.

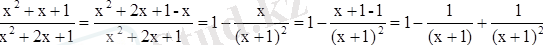
u деп белгілейміз:

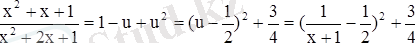
Функцияның кіші мәні Оны мына теңдеуді шешіп таптық.
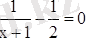
х = 1
Кесте құрып, графигін саламыз.
х
-3
-2
-32
-1
-12
0
1
2
3
...
у
74
3
7
Х
3
1
34
79
1316
...
Если аргумент х тің мәні -1 ге ұмтылғанда (слева или справа), у шексіз өседі.
Теперь посмотрим, как будет вести себя у, когда х +шексіздікке ж2не - шексіздікке ұмтылғанда функция 1- ге ұмтылады.

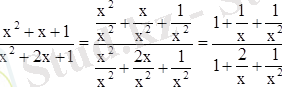
Функцияның экстремумдарын табу

2. суретте у = f(х) графигі берілген.
Функцияның анықталу облысын анықта

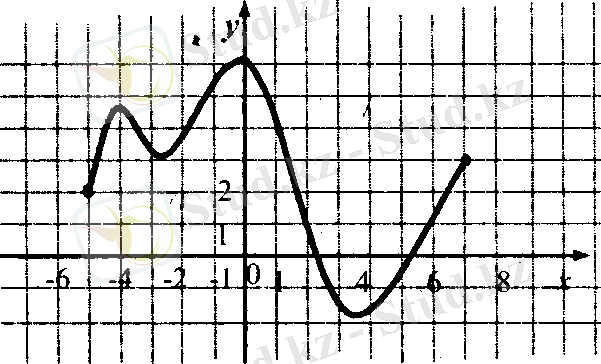
1) [- 5; 7]
2) [- 2; 6]
3) [- 2; 4]
4) [0; 7]

Жауабы:1

3. у = f(х) функцияның графигі [ - 6; 4] аралықта.
f(х) 0 анықта

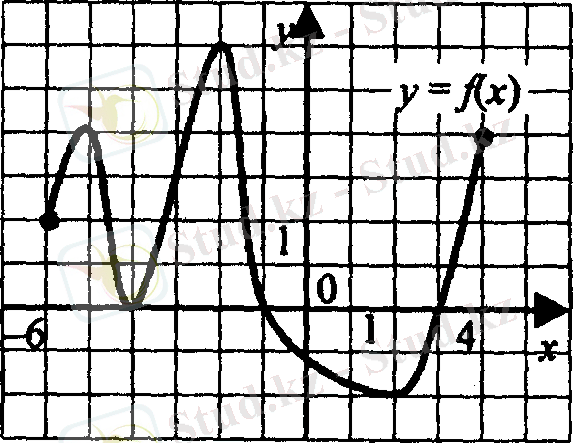
1) [- 6; - 5] [- 4; - 2] [2; 4]
2) [- 6; - 5] [- 4; 2] [3; 4]
3) [- 6; - 4) (- 4; - 1) (3; 4 ]
4)[- 6;- 1) (3;4]
Жауабы: 4

4.Функцияның қай аралықта кемімелі

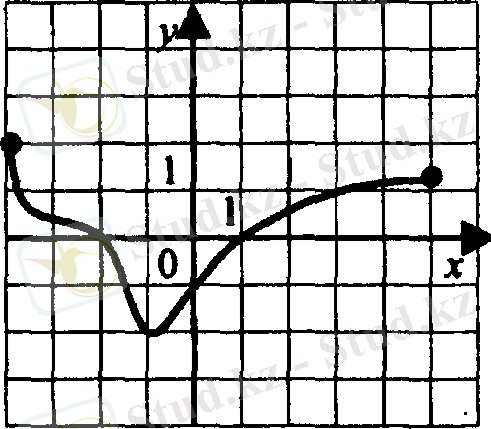
1)[ - 4; 0]
2)[ - 4; 1]
3)[ - 2; 1]
4)[ - 4; - 1]
Жауабы: 4

6-7 практикалық сабақ.
Экстремумға берілген қолданбалы есептерді шешудің геометриялық және алгебралық тәсілдері

Есеп №1
Жасаушысы 15 см болатын конустық шұңқыр жасау керек, көлемі ең үлкен болу үшін оның биіктігі қандай болуы керек?
Шешуі:
l=15

15

R
R2+h2=225 R2=225-h2
V=13PIR2h=13PI225-h2h
V(h)=PI3225h-h3
V'(h)=225-3h2=375-h2=0 h2=75 h=53
Жауабы: 53

критерий
дескриптор
балл
1
Пифагор теоремасы арқылы радиусты табады
1
2
Конустың формулаларын пайдаланады
1
3
Көлемнің туындысын табу арқылы, биіктікті анықтайды
1

Есеп №2
Диагоналы 4 дм болатын барлық тіктөртбұрышты қораптардың ішінен ауданы ең үлкені болатын қораптың қабырғасын табыңыз.
Шешуі:
аxb=S
a2+b2=42 b2=16-a2
S=a16-a2 S'=16-2a216-a2=0
16-2a2=0 a2=8 a=+-22
a0 a=22 b=22
S=22x22=8
Жауабы: 8
критерий
дескриптор
балл
1
Пифагор теоремасы арқылы қабырғаны табады
1
2
Ауданды табу формулаларын пайдаланады
1
3
Ауданның туындысын табу арқылы қабырғасын анықтайды
1

критерий
дескриптор
балл
1
Цилиндрдің формулаларын пайдаланып, көлемін табады
1
2
Көлемін пайдаланып, қанша балық жіберуге болатынын табады
1

Есеп №3
Айжан электронды сағаттың сағаттық және минуттық сандарының цифрларының қосындыларын тауып өзара қосты. Қосындының ең үлкен мәнін көрсетіңіз.
Шешуі:
19:59 ды көрсеткенде үлкен цифрлар
1+9+5+9 = 24
Жауабы: 24
Есеп №4
Кестеде әр жылдардағы Шкода және Шевролет автомобильдерінің бағаларының графигі берілген. Тік осьте көліктің бағасы, көлденең осьте жылдар көрсетілген. Жыл бойы екі автомобильдің де бағалары 4000000-нан кем емес болған жылдарды көрсетіңіз.

Жауабы: 2009 жыл

5-есеп. Жеделхат құнын пошта қызметкерлері келесі ереже бойынша есептейді: әр сөз үшін 5 рубль және жеделхат жіберу үшін тағы 20 рубль. Егер жеделхаттағы сөздер саны 17 = х = 40 теңсіздігін шешу арқылы анықталса, жеделхаттың ең жоғары және ең төменгі құны қандай болуы мүмкін?
Есептің шешімі 5х + 20 өрнектің ең үлкен және ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.