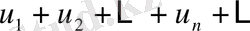Екі және үш еселі интегралдар мен сандық қатарлардың жинақталу критерийлері


1. Тікбұрышты координаталармен берілген екі еселі интеграл
Айталық,
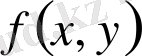 функциясы
функциясы
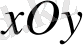 жазықтығының
жазықтығының
 шенелген облысында анықталсын.
шенелген облысында анықталсын.
 облысын аудандары
облысын аудандары
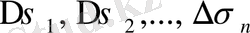 және диаметрлері
және диаметрлері
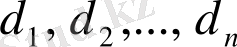 (лблыстың диаметрі деп осы облыстың шекарасының ең қашақ екі нүктесінің арасының ұзындығын айтады) болатын "
(лблыстың диаметрі деп осы облыстың шекарасының ең қашақ екі нүктесінің арасының ұзындығын айтады) болатын "
 " облыстарға бөлшектейік. Әрбір элементар облыста кез келген
" облыстарға бөлшектейік. Әрбір элементар облыста кез келген
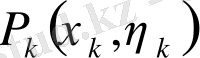 нүктесін таңдап алайық және функцияның
нүктесін таңдап алайық және функцияның
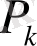 нүктесіндегі мәнін осы облыстың ауданына көбейтейік.
нүктесіндегі мәнін осы облыстың ауданына көбейтейік.
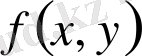 функциясы үшін
функциясы үшін
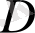 облысы бойынша
интегралдық қосынды
деп келесі қосындыны айтады:
облысы бойынша
интегралдық қосынды
деп келесі қосындыны айтады:
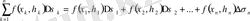 (1)
(1)
Егер
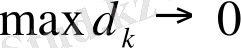 ұмтылғанда интегралдық қосындының
ұмтылғанда интегралдық қосындының
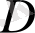 облысын элементар бөлшектерге бөлу әдісінен және осы облыста
облысын элементар бөлшектерге бөлу әдісінен және осы облыста
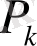 нүктелерін таңдап алудан тәуелсі анықталған ақырлы шегі болса, яғни
нүктелерін таңдап алудан тәуелсі анықталған ақырлы шегі болса, яғни
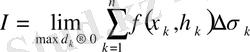 (2)
(2)
онда бұл шек
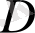 облысындағы
облысындағы
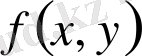 функциясының
екі еселі интегралы
деп аталады және былай белгіленеді:
функциясының
екі еселі интегралы
деп аталады және былай белгіленеді:
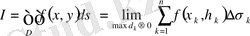 (3)
(3)
Ескерту. Егер
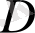 облысында
облысында
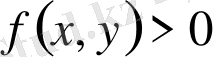 болса, онда
болса, онда
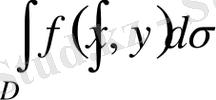 екі еселі интеграл - жоғарыдан
екі еселі интеграл - жоғарыдан
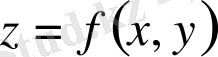 бетімен, бүйірінен құраушылары
бетімен, бүйірінен құраушылары
 осімен параллель болатвн цилиндрлік бетпен және төменнен
осімен параллель болатвн цилиндрлік бетпен және төменнен
 жазақтығының
жазақтығының
 облысымен шектелген цилиндрлік дененің көлеміне тең болады.
облысымен шектелген цилиндрлік дененің көлеміне тең болады.
 .
.
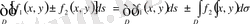
 .
.
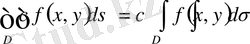 , мұнда
, мұнда
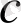 - тұрақты сан.
- тұрақты сан.
 . Егер
. Егер
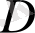 интегралдау облысы
интегралдау облысы
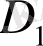 және
және
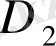 облыстарына бөлінсе, онда
облыстарына бөлінсе, онда

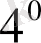 .
Екі еселі интегралды бағалау.
Егер
.
Екі еселі интегралды бағалау.
Егер
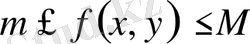 болса, онда
болса, онда
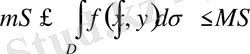 , мұнда
, мұнда
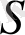 -
-
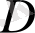 облысының ауданы, ал
облысының ауданы, ал
 және
және
 -
-
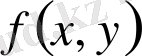 функциясының
функциясының
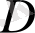 облысындағы сәйкес ең кіші және ең үлкен мәндері.
облысындағы сәйкес ең кіші және ең үлкен мәндері.
Интегралдау облысының негізгі екі түрі болады.
1.
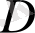 интегралдау облысы сол жақтан және оң жақтан
интегралдау облысы сол жақтан және оң жақтан
 ,
,
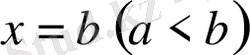 түзулерімен, ал төменнен және жоғарыдан әрқайсысы вертикаль түзумен тек бір нүктеде қиылысатын
түзулерімен, ал төменнен және жоғарыдан әрқайсысы вертикаль түзумен тек бір нүктеде қиылысатын
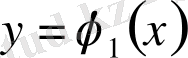 және
және
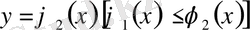 үзіліссіз қисықтармен шектелген (1-сурет) .
үзіліссіз қисықтармен шектелген (1-сурет) .
Мұндай облыс үшін екі еселі интеграл келесі формула бойынша есептеледі:
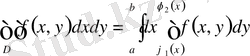
және де алдымен ішкі интеграл
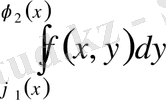 ,
,
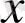 -ті тұрақты деп алып есептеледі.
-ті тұрақты деп алып есептеледі.
2.
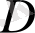 интегралдау облысы төменнен және жоғарыдан
интегралдау облысы төменнен және жоғарыдан
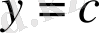 және
және
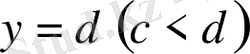 түзулерімен, ал сол жақтан және оң жақтан әрқайсысы горизонталь түзумен тек бір нүктеде қиылысатын үзіліссіз
түзулерімен, ал сол жақтан және оң жақтан әрқайсысы горизонталь түзумен тек бір нүктеде қиылысатын үзіліссіз
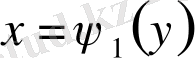 және
және
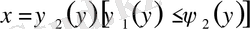 қисықтарымен шектелген (2-сурет) .
қисықтарымен шектелген (2-сурет) .
1-сурет 2-сурет
Мұндай облыс үшін екі еселі интеграл келесі формула бойынша есептеледі:
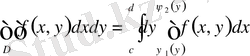
және де алдымен ішкі интеграл
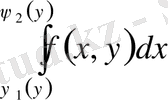 ,
,
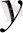 -ті тұрақты деп алып есептеледі.
-ті тұрақты деп алып есептеледі.
Көрсетілген формулалардың оң жақтары қайталанбалы интегралдар деп аталады. Жалпы жағдайда интегралдау облысы бөлшектеу жолымен жоғарыдағы негізгі интегралдарға келтіріледі
2. Екі еселі интегралда айнымалыларды ауыстыру
Полярлық координаталардағы екі еселі интеграл.
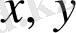 тікбұрышты координаталарымен берілген екі еселі интегралды тікбұрышты координаталармен
тікбұрышты координаталарымен берілген екі еселі интегралды тікбұрышты координаталармен
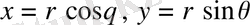 өрнектері арқылы байланысатын
өрнектері арқылы байланысатын
 полярлық координаталарға көшіру келесі формула бойынша іске асырылады:
полярлық координаталарға көшіру келесі формула бойынша іске асырылады:
.
Егер
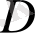 интегралдау облысы полюстен басталатын
интегралдау облысы полюстен басталатын
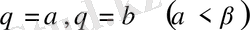 сәулелерімен және
сәулелерімен және
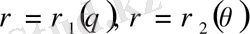 қисықтарымен (мұнда
қисықтарымен (мұнда
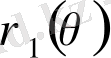 және
және
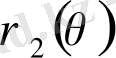 -
-
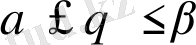 және
және
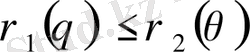 болғанда бірмәнді функциялар) шектелсе, онда екі еселі интеграл келесі формула бойынша есептеледі:
болғанда бірмәнді функциялар) шектелсе, онда екі еселі интеграл келесі формула бойынша есептеледі:
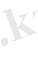
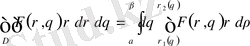
мұнда
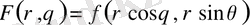 және де алдымен ішкі интеграл
және де алдымен ішкі интеграл
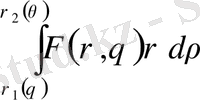 ,
,
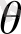 -ны тұрақты деп алып есептеледі.
-ны тұрақты деп алып есептеледі.
Қисық сызықты координаталардағы екі еселі интеграл.
Айталық екі еселі интеграл
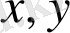 тікбұрышты координаталардан, осы тікбұрышты координаталармен
тікбұрышты координаталардан, осы тікбұрышты координаталармен
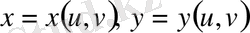 өрнектері арқылы байланысатын
өрнектері арқылы байланысатын
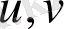 қисық сызықты координаталарға ауыстырылсын, мұнда
қисық сызықты координаталарға ауыстырылсын, мұнда
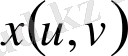 және
және
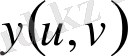 функцияларының
функцияларының
 жазықтығының
жазықтығының
 облысында үзіліссіз дербес туындылары бар және түрлендірудің якобиан деп аталатын анықтауышы
облысында үзіліссіз дербес туындылары бар және түрлендірудің якобиан деп аталатын анықтауышы
 облысында нөлге тең емес:
облысында нөлге тең емес:
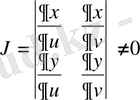
Сонымен бірге
 жазықтығының
жазықтығының
 облысы мен
облысы мен
 жазықтығының
жазықтығының
 облысының нүктелерінің арасында өзара бірмәнді және екі жаққа да үзіліссіз сәйкестік орнатылады (5-сурет) .
облысының нүктелерінің арасында өзара бірмәнді және екі жаққа да үзіліссіз сәйкестік орнатылады (5-сурет) .
5-сурет
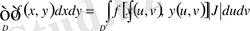
Полярлық координаталар үшін:
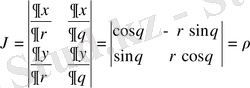 .
.
3. Жазық фигураның ауданын есетеу
 облысымен шектелген
жазық фигураның ауданы
келесі формула бойынша есептеледі:
облысымен шектелген
жазық фигураның ауданы
келесі формула бойынша есептеледі:

Егер
 облысы, мысалы,
облысы, мысалы,
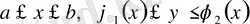 теңсіздіктерімен анықталса, онда
теңсіздіктерімен анықталса, онда
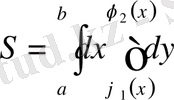
Егер
 облысы полярлық координаталарда
облысы полярлық координаталарда
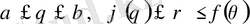 теңсіздіктерімен анықталса, онда
теңсіздіктерімен анықталса, онда
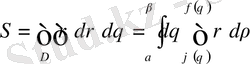 .
.
4. Дененің көлемін есептеу
Жоғарыдан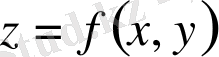 үзіліссіз бетпен, төменнен
үзіліссіз бетпен, төменнен
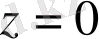 жазықтығымен және бүйірінен
жазықтығымен және бүйірінен
 жазықтығында
жазықтығында
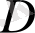 облысын қиятын цилиндрлік бетпен шектелген цилиндрлік
дененің көлемі
келесі формула бойынша есептеледі:
облысын қиятын цилиндрлік бетпен шектелген цилиндрлік
дененің көлемі
келесі формула бойынша есептеледі:
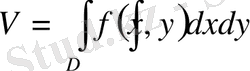
5. Беттің ауданын есептеу
Егер жылтыр бет
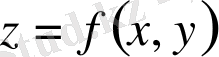 теңдеуі арқылы берілсе, онда
беттің ауданы
келесі формула бойынша есептеледі:
теңдеуі арқылы берілсе, онда
беттің ауданы
келесі формула бойынша есептеледі:
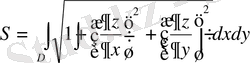 ,
,
мұнда
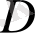 берілген беттің
берілген беттің
 жазықтығындағы проекциясы.
жазықтығындағы проекциясы.
Осылайша, егер бет
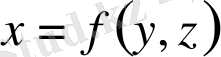 теңдеуі арқылы берілсе, онда:
теңдеуі арқылы берілсе, онда:
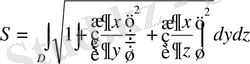 ,
,
мұнда
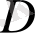 берілген беттің
берілген беттің
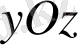 жазықтығындағы проекциясы.
жазықтығындағы проекциясы.
Егер беттің теңдеуі
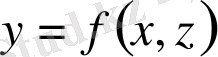 түрінде бнрілсе, онда:
түрінде бнрілсе, онда:
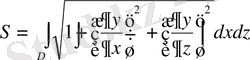 ,
,
мұнда
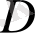 берілген беттің
берілген беттің
 жазықтығындағы проекциясы.
жазықтығындағы проекциясы.
6. Екі еселі интегралдың физикада қолданылуы
Егер пластинка
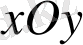 жазықтығының
жазықтығының
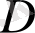 облысын алып жатса және оның
облысын алып жатса және оның
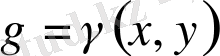 беттік тығыздығы айнымалы болса, онда пластинканың
беттік тығыздығы айнымалы болса, онда пластинканың
 массасы
екі еселі интеграл арқылы былай өрнектеледі:
массасы
екі еселі интеграл арқылы былай өрнектеледі:
 .
.
Пластинканың
 және
және
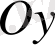 осьтеріне қатысты
статикалық моменті
келесі формулалар бойынша табылады:
осьтеріне қатысты
статикалық моменті
келесі формулалар бойынша табылады:
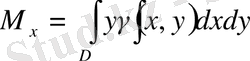 ,
,
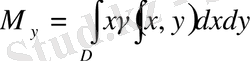 .
.
Пластинка біртекті болғанда
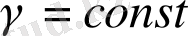 .
.
Пластиканың ауырлық центрінің координаталарын келесі формулалар арқылы есептеуге болады:
 ,
,
мұнда
 - пластинканың массасы, ал
- пластинканың массасы, ал
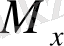 ,
,
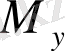 - оның координаталар осьтеріне қатысты статикалық моменттері.
- оның координаталар осьтеріне қатысты статикалық моменттері.
Пластинка біртекті болса, онда ол формулалар келесі түрде болады:
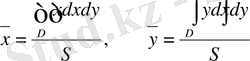 ,
,
мұнда
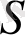 -
-
 облысының ауданы.
облысының ауданы.
Пластинканың
 және
және
 осьтеріне қатысты
инерция моменттері
келесі формулалар бойынша табылады:
осьтеріне қатысты
инерция моменттері
келесі формулалар бойынша табылады:
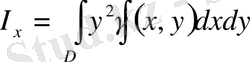 ,
,
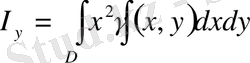 ,
,
ал координаталар бас нүктесіне қатысты инерция моменті келесі формула бойынша есептеледі:
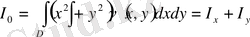 .
.
Бұл формулаларда
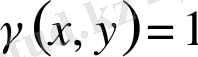 деп алсақ, жазық фигураның геометриялық инерция моменттерін есептеуге арналған формулаларды аламыз.
деп алсақ, жазық фигураның геометриялық инерция моменттерін есептеуге арналған формулаларды аламыз.
Үш еселі интеграл
Айталық,
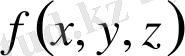 функциясы шектелген тұйық кеңістіктік
функциясы шектелген тұйық кеңістіктік
 облысында анықталған болсын.
облысында анықталған болсын.
 облысын кез келген әдіспен диаметрлері
облысын кез келген әдіспен диаметрлері
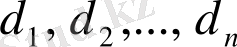 және көлемдері
және көлемдері
 болатын
болатын
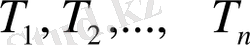 -
-
 элементар облыстарға бөлшектейік. Әрбір элементар облыста кез келген
элементар облыстарға бөлшектейік. Әрбір элементар облыста кез келген
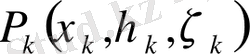 нүктесін таңдап алайық және функцияның
нүктесін таңдап алайық және функцияның
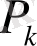 нүктесіндегі мәнін осы облыстың көлеміне көбейтейік.
нүктесіндегі мәнін осы облыстың көлеміне көбейтейік.
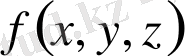 функциясы үшін
функциясы үшін
 облысы бойынша
интегралдық қосындысы
деп келесі түрдегі қосындыны айтады:
облысы бойынша
интегралдық қосындысы
деп келесі түрдегі қосындыны айтады:
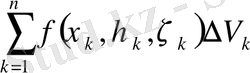 .
.
Интегралдық қосындының
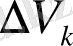 элементар облыстарының диаметрлерінің ең үлкені нөлге ұмтылған кездегі шегін
элементар облыстарының диаметрлерінің ең үлкені нөлге ұмтылған кездегі шегін
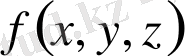 функциясынан
функциясынан
 облысы бойынша алынған үш еселі интеграл деп атайды және ол келесі түрде белгіленеді:
облысы бойынша алынған үш еселі интеграл деп атайды және ол келесі түрде белгіленеді:
 .
.
Бұл түрдегі ақырлы шек тек қана шектелген функция үшін ғана бар болады. .
Егер
 облысында
облысында
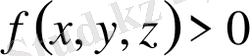 болса, онда
болса, онда
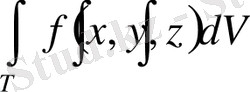 үш еселі интегралы
үш еселі интегралы
 облысын алып жататын және
облысын алып жататын және
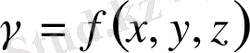 тығыздығы айнымалы болатын дененің массасы болады (үш кеселі интегралдың физикалық мағнасы) .
тығыздығы айнымалы болатын дененің массасы болады (үш кеселі интегралдың физикалық мағнасы) .
Үш еселі интегралдың негізгі қасиеттері екі еселі интегралдың қасиеттеріне сәйкес болады.
Декарттық координаталарда үш еселі интеграл келесі түрде болады:
 .
.
Айталық,
 интегралдау облысы
интегралдау облысы
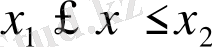 ,
,
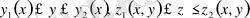 (мұнда
(мұнда
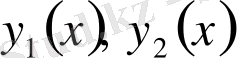 ,
,
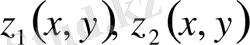 - үзіліссіз функциялар) теңсіздіктерімен анықталсын.
- үзіліссіз функциялар) теңсіздіктерімен анықталсын.
Сонда
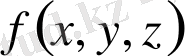 функциясынан
функциясынан
 облысы бойынша алынған үш еселі интеграл келесі формуланың көмегімен есептеледі:
облысы бойынша алынған үш еселі интеграл келесі формуланың көмегімен есептеледі:
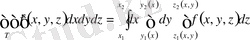 .
.
Егер үш еселі интегралды есептегенде
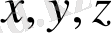 айнымалылларынан осы айнымалылармен
айнымалылларынан осы айнымалылармен
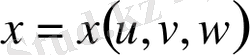 ,
,
 өрнектері арқылы байланысатын
өрнектері арқылы байланысатын
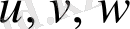 айнымалыларына көшу керек болса (мұнда
айнымалыларына көшу керек болса (мұнда
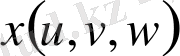 ,
,
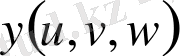 ,
,
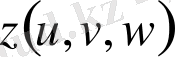 - өздерінің бірінші ретті дербес туындыларымен бірге үзіліссіз функциялар),
- өздерінің бірінші ретті дербес туындыларымен бірге үзіліссіз функциялар),
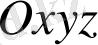 кеңістігінің
кеңістігінің
 облысы мен
облысы мен
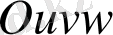 кеңістігінің
кеңістігінің
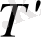 облысының нүктелерінің арасында өзара бірмәнді және екі жаққа да үзіліссіз сәйкестік орнатылады және
облысының нүктелерінің арасында өзара бірмәнді және екі жаққа да үзіліссіз сәйкестік орнатылады және
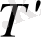 облысында
облысында
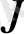 якобианы нөлге айналмайды:
якобианы нөлге айналмайды:
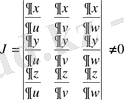 ,
,
онда келесі формуланы пайдалану керек. :
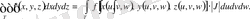
Дербес жағдайда,
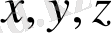 декарттық координаталардан осы координаталармен
декарттық координаталардан осы координаталармен
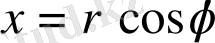 ,
,
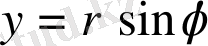 ,
,
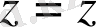 (
(
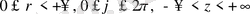 ) өрнектері арқылы байланысатын
) өрнектері арқылы байланысатын
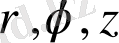 цилиндрлік координаталарға көшу кезінде түрлендіру якобианы
цилиндрлік координаталарға көшу кезінде түрлендіру якобианы
 болады және
үш еселі интегралды цилиндрлік координаталарға түрлендіру формуласы
келесі түрде болады (17-сурет) :
болады және
үш еселі интегралды цилиндрлік координаталарға түрлендіру формуласы
келесі түрде болады (17-сурет) :

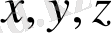 декарттық координаталардан осы координаталармен
декарттық координаталардан осы координаталармен
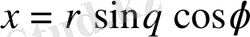 ,
,
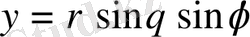 ,
,
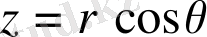 (
(
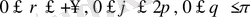 ) өрнектері арқылы байланысатын
) өрнектері арқылы байланысатын
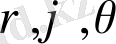 сфералық координаталарға көшу кезінде түрлендіру якобианы
сфералық координаталарға көшу кезінде түрлендіру якобианы
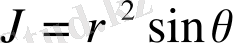 болады және
үш еселі интегралды сфералық координаталарға түрлендіру
формуласы келесі түрде болады (18-сурет) :
болады және
үш еселі интегралды сфералық координаталарға түрлендіру
формуласы келесі түрде болады (18-сурет) :

17-сурет 18-сурет
8. Үш еселі интегралдың қолданылулары
 облысында жататын
дененің көлемі
келесі формула бойынша есептеледі:
облысында жататын
дененің көлемі
келесі формула бойынша есептеледі:
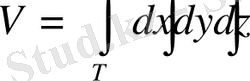 .
.
Егер дененің тығыздығы айнымалы болса, яғни
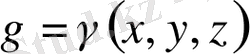 , онда
, онда
 облысында жататын
дененің массасы
келесі формула бойынша есептеледі:
облысында жататын
дененің массасы
келесі формула бойынша есептеледі:
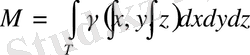 .
.
Дененің ауырлық центрінің координаталары мына формулалар бойынша анықталады:
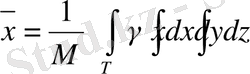 ,
,
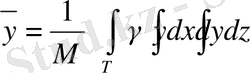 ,
,
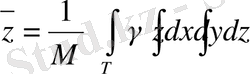 .
.
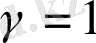 болғанда
болғанда
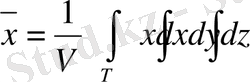 ,
,
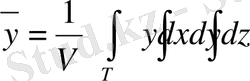 ,
,
 .
.
(
 -геометриялық ауырлық центрінің координаталары) .
-геометриялық ауырлық центрінің координаталары) .
Координата осьтеріне қатысты инерция моменттері (геометриялық) сәйкесінше төмендегідей болады:
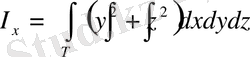 ,
,
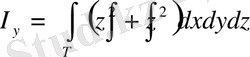 ,
,
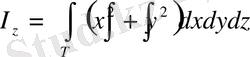 .
.
9. Параметрден тәуелді интегралдар.
Интеграл таңбасы астында дифференциалдау және интегралдау
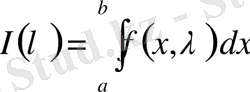 (1)
(1)
интегралын қарастырамыз, мұнда
 - айнымалы параметр, ал
- айнымалы параметр, ал
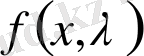 -
-
 аралығында
аралығында
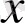 -тің барлық мәндері үшін және
-тің барлық мәндері үшін және
 -ның
-ның
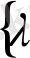 жиынындағы барлық мәндері үшін анықталған екі айнымалының функциясы. Бұл шарттар орындалғанда (1) интеграл
жиынындағы барлық мәндері үшін анықталған екі айнымалының функциясы. Бұл шарттар орындалғанда (1) интеграл
 параметрінен тәуелді функция болады.
параметрінен тәуелді функция болады.
 функциясының
функциясының
 параметрі бойынша туындысы туралы сұрақтың маңызы зор. Айталық,
параметрі бойынша туындысы туралы сұрақтың маңызы зор. Айталық,
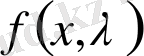 функциясы және
функциясы және
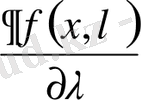 дербес туындысы
дербес туындысы
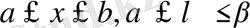 тікбұрышында үзіліссіз болсын. Бұл жағдайда келесі туынды анықталады:
тікбұрышында үзіліссіз болсын. Бұл жағдайда келесі туынды анықталады:
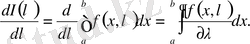 . (2)
. (2)
Егер туындының (
 бойынша) және интегралдың (
бойынша) және интегралдың (
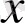 бойынша) таңбаларын ауыстыруға болатын болса, онда (1) функциясын
параметр бойынша интеграл таңбасының астында дифференциалдауға
болады дейді. (2) формулада интегралдау шекаралары
бойынша) таңбаларын ауыстыруға болатын болса, онда (1) функциясын
параметр бойынша интеграл таңбасының астында дифференциалдауға
болады дейді. (2) формулада интегралдау шекаралары
 және
және
 -
-
 параметрінен тәуелсіз деп есептеледі. Егер
параметрінен тәуелсіз деп есептеледі. Егер
 және
және
 -
-
 параметрінен тәуелді болса, онда
параметрінен тәуелді болса, онда
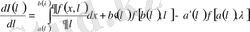 . (3)
. (3)
Айталық,
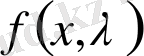 функциясы қандай да бір
функциясы қандай да бір
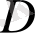 облысында
облысында
 -ның барлық мәндері үшін және
-ның барлық мәндері үшін және
 -ның барлық мәндері үшін берілген болсын¸ және де әрбір
-ның барлық мәндері үшін берілген болсын¸ және де әрбір
 үшін бұл облыста келесі интеграл анықталсын:
үшін бұл облыста келесі интеграл анықталсын:

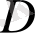 облысында бұл интеграл
облысында бұл интеграл
 -
ға қатысты бірқалыпты
-
ға қатысты бірқалыпты
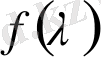 -
ға ұмтылса, онда
-
ға ұмтылса, онда
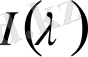 интегралы
интегралы
 -ға қатысты параметрдің берілген мәндері үшін
бірқалыпты жинақталады
деп атайды.
-ға қатысты параметрдің берілген мәндері үшін
бірқалыпты жинақталады
деп атайды.
Бұдан кез келген
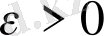 үшін
үшін
 -
дан тәуелді
-
дан тәуелді
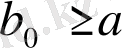 саны табылып,
саны табылып,
 болған кезде
болған кезде
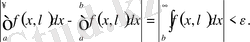
теңсіздігі
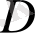 облысында
облысында
 -ның барлық мәндері үшін орындалады.
-ның барлық мәндері үшін орындалады.
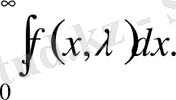 меншіксіз интегралын параметр бойынша дифференциалдау үшін,
меншіксіз интегралын параметр бойынша дифференциалдау үшін,
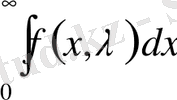 және
және
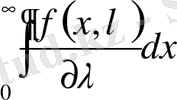 интегралдарының
интегралдарының
 болған кезде бар болуы қажет.
болған кезде бар болуы қажет.
(1) анықталған интегралды
 параметрі бойынша
параметрі бойынша
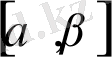 аралығында интеграл таңбасы астында интегралдау формуласы келесі түрде болады:
аралығында интеграл таңбасы астында интегралдау формуласы келесі түрде болады:
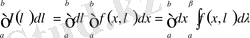 . (4)
. (4)
Интеграл астындағы функция
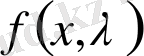 ақырлы интегралдау облысында екі айнымалының үзіліссіз функциясы болу керек. Интегралдау облысы ақырсыз болғанда қаталама меншіксіз интеграл шығады.
ақырлы интегралдау облысында екі айнымалының үзіліссіз функциясы болу керек. Интегралдау облысы ақырсыз болғанда қаталама меншіксіз интеграл шығады.
Үш еселі интеграл
Айталық,
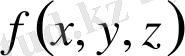 функциясы шектелген тұйық кеңістіктік
функциясы шектелген тұйық кеңістіктік
 облысында анықталған болсын.
облысында анықталған болсын.
 облысын кез келген әдіспен диаметрлері
облысын кез келген әдіспен диаметрлері
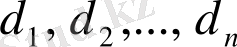 және көлемдері
және көлемдері
 болатын
болатын
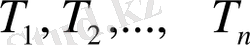 -
-
 элементар облыстарға бөлшектейік. Әрбір элементар облыста кез келген
элементар облыстарға бөлшектейік. Әрбір элементар облыста кез келген
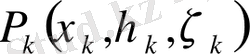 нүктесін таңдап алайық және функцияның
нүктесін таңдап алайық және функцияның
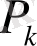 нүктесіндегі мәнін осы облыстың көлеміне көбейтейік.
нүктесіндегі мәнін осы облыстың көлеміне көбейтейік.
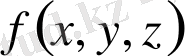 функциясы үшін
функциясы үшін
 облысы бойынша
интегралдық қосындысы
деп келесі түрдегі қосындыны айтады:
облысы бойынша
интегралдық қосындысы
деп келесі түрдегі қосындыны айтады:
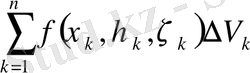 .
.
Интегралдық қосындының
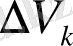 элементар облыстарының диаметрлерінің ең үлкені нөлге ұмтылған кездегі шегін
элементар облыстарының диаметрлерінің ең үлкені нөлге ұмтылған кездегі шегін
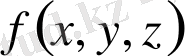 функциясынан
функциясынан
 облысы бойынша алынған үш еселі интеграл деп атайды және ол келесі түрде белгіленеді:
облысы бойынша алынған үш еселі интеграл деп атайды және ол келесі түрде белгіленеді:
 .
.
Бұл түрдегі ақырлы шек тек қана шектелген функция үшін ғана бар болады. .
Егер
 облысында
облысында
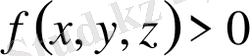 болса, онда
болса, онда
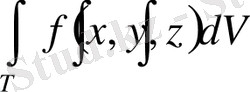 үш еселі интегралы
үш еселі интегралы
 облысын алып жататын және
облысын алып жататын және
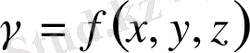 тығыздығы айнымалы болатын дененің массасы болады (үш кеселі интегралдың физикалық мағнасы) .
тығыздығы айнымалы болатын дененің массасы болады (үш кеселі интегралдың физикалық мағнасы) .
Үш еселі интегралдың негізгі қасиеттері екі еселі интегралдың қасиеттеріне сәйкес болады.
Декарттық координаталарда үш еселі интеграл келесі түрде болады:
 .
.
Айталық,
 интегралдау облысы
интегралдау облысы
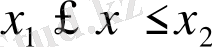 ,
,
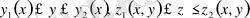 (мұнда
(мұнда
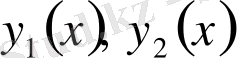 ,
,
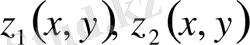 - үзіліссіз функциялар) теңсіздіктерімен анықталсын.
- үзіліссіз функциялар) теңсіздіктерімен анықталсын.
Сонда
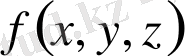 функциясынан
функциясынан
 облысы бойынша алынған үш еселі интеграл келесі формуланың көмегімен есептеледі:
облысы бойынша алынған үш еселі интеграл келесі формуланың көмегімен есептеледі:
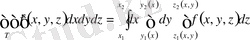 .
.
Егер үш еселі интегралды есептегенде
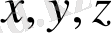 айнымалылларынан осы айнымалылармен
айнымалылларынан осы айнымалылармен
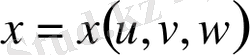 ,
,
 өрнектері арқылы байланысатын
өрнектері арқылы байланысатын
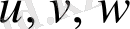 айнымалыларына көшу керек болса (мұнда
айнымалыларына көшу керек болса (мұнда
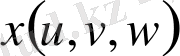 ,
,
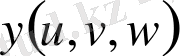 ,
,
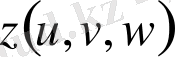 - өздерінің бірінші ретті дербес туындыларымен бірге үзіліссіз функциялар),
- өздерінің бірінші ретті дербес туындыларымен бірге үзіліссіз функциялар),
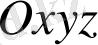 кеңістігінің
кеңістігінің
 облысы мен
облысы мен
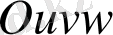 кеңістігінің
кеңістігінің
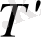 облысының нүктелерінің арасында өзара бірмәнді және екі жаққа да үзіліссіз сәйкестік орнатылады және
облысының нүктелерінің арасында өзара бірмәнді және екі жаққа да үзіліссіз сәйкестік орнатылады және
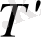 облысында
облысында
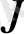 якобианы нөлге айналмайды:
якобианы нөлге айналмайды:
 ,
,
онда келесі формуланы пайдалану керек. :
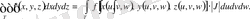
Дербес жағдайда,
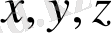 декарттық координаталардан осы координаталармен
декарттық координаталардан осы координаталармен
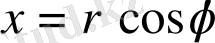 ,
,
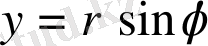 ,
,
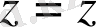 (
(
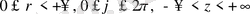 ) өрнектері арқылы байланысатын
) өрнектері арқылы байланысатын
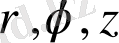 цилиндрлік координаталарға көшу кезінде түрлендіру якобианы
цилиндрлік координаталарға көшу кезінде түрлендіру якобианы
 болады және
үш еселі интегралды цилиндрлік координаталарға түрлендіру формуласы
келесі түрде болады (17-сурет) :
болады және
үш еселі интегралды цилиндрлік координаталарға түрлендіру формуласы
келесі түрде болады (17-сурет) :

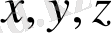 декарттық координаталардан осы координаталармен
декарттық координаталардан осы координаталармен
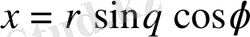 ,
,
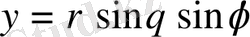 ,
,
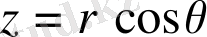 (
(
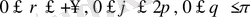 ) өрнектері арқылы байланысатын
) өрнектері арқылы байланысатын
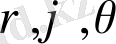 сфералық координаталарға көшу кезінде түрлендіру якобианы
сфералық координаталарға көшу кезінде түрлендіру якобианы
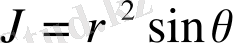 болады және
үш еселі интегралды сфералық координаталарға түрлендіру
формуласы келесі түрде болады (18-сурет) :
болады және
үш еселі интегралды сфералық координаталарға түрлендіру
формуласы келесі түрде болады (18-сурет) :

17-сурет 18-сурет
8. Үш еселі интегралдың қолданылулары
 облысында жататын
дененің көлемі
келесі формула бойынша есептеледі:
облысында жататын
дененің көлемі
келесі формула бойынша есептеледі:
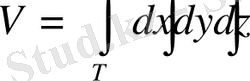 .
.
Егер дененің тығыздығы айнымалы болса, яғни
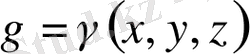 , онда
, онда
 облысында жататын
дененің массасы
келесі формула бойынша есептеледі:
облысында жататын
дененің массасы
келесі формула бойынша есептеледі:
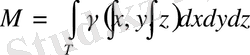 .
.
Дененің ауырлық центрінің координаталары мына формулалар бойынша анықталады:
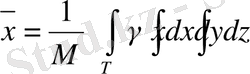 ,
,
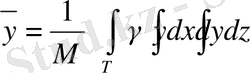 ,
,
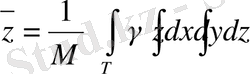 .
.
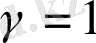 болғанда
болғанда
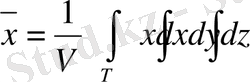 ,
,
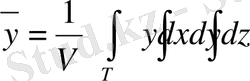 ,
,
 .
.
(
 -геометриялық ауырлық центрінің координаталары) .
-геометриялық ауырлық центрінің координаталары) .
Координата осьтеріне қатысты инерция моменттері (геометриялық) сәйкесінше төмендегідей болады:
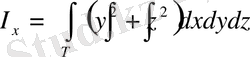 ,
,
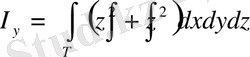 ,
,
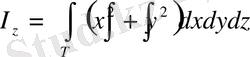 .
.
9. Параметрден тәуелді интегралдар.
Интеграл таңбасы астында дифференциалдау және интегралдау
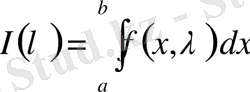 (1)
(1)
интегралын қарастырамыз, мұнда
 - айнымалы параметр, ал
- айнымалы параметр, ал
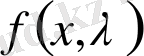 -
-
 аралығында
аралығында
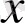 -тің барлық мәндері үшін және
-тің барлық мәндері үшін және
 -ның
-ның
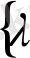 жиынындағы барлық мәндері үшін анықталған екі айнымалының функциясы. Бұл шарттар орындалғанда (1) интеграл
жиынындағы барлық мәндері үшін анықталған екі айнымалының функциясы. Бұл шарттар орындалғанда (1) интеграл
 параметрінен тәуелді функция болады.
параметрінен тәуелді функция болады.
 функциясының
функциясының
 параметрі бойынша туындысы туралы сұрақтың маңызы зор. Айталық,
параметрі бойынша туындысы туралы сұрақтың маңызы зор. Айталық,
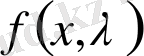 функциясы және
функциясы және
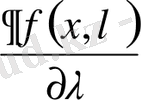 дербес туындысы
дербес туындысы
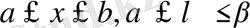 тікбұрышында үзіліссіз болсын. Бұл жағдайда келесі туынды анықталады:
тікбұрышында үзіліссіз болсын. Бұл жағдайда келесі туынды анықталады:
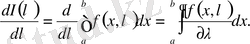 . (2)
. (2)
Егер туындының (
 бойынша) және интегралдың (
бойынша) және интегралдың (
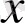 бойынша) таңбаларын ауыстыруға болатын болса, онда (1) функциясын
параметр бойынша интеграл таңбасының астында дифференциалдауға
болады дейді. (2) формулада интегралдау шекаралары
бойынша) таңбаларын ауыстыруға болатын болса, онда (1) функциясын
параметр бойынша интеграл таңбасының астында дифференциалдауға
болады дейді. (2) формулада интегралдау шекаралары
 және
және
 -
-
 параметрінен тәуелсіз деп есептеледі. Егер
параметрінен тәуелсіз деп есептеледі. Егер
 және
және
 -
-
 параметрінен тәуелді болса, онда
параметрінен тәуелді болса, онда
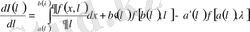 . (3)
. (3)
Айталық,
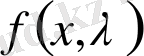 функциясы қандай да бір
функциясы қандай да бір
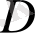 облысында
облысында
 -ның барлық мәндері үшін және
-ның барлық мәндері үшін және
 -ның барлық мәндері үшін берілген болсын¸ және де әрбір
-ның барлық мәндері үшін берілген болсын¸ және де әрбір
 үшін бұл облыста келесі интеграл анықталсын:
үшін бұл облыста келесі интеграл анықталсын:

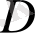 облысында бұл интеграл
облысында бұл интеграл
 -
ға қатысты бірқалыпты
-
ға қатысты бірқалыпты
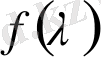 -
ға ұмтылса, онда
-
ға ұмтылса, онда
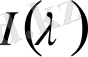 интегралы
интегралы
 -ға қатысты параметрдің берілген мәндері үшін
бірқалыпты жинақталады
деп атайды.
-ға қатысты параметрдің берілген мәндері үшін
бірқалыпты жинақталады
деп атайды.
Бұдан кез келген
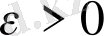 үшін
үшін
 -
дан тәуелді
-
дан тәуелді
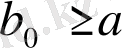 саны табылып,
саны табылып,
 болған кезде
болған кезде
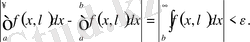
теңсіздігі
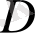 облысында
облысында
 -ның барлық мәндері үшін орындалады.
-ның барлық мәндері үшін орындалады.
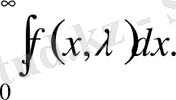 меншіксіз интегралын параметр бойынша дифференциалдау үшін,
меншіксіз интегралын параметр бойынша дифференциалдау үшін,
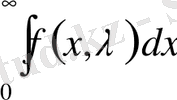 және
және
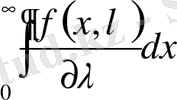 интегралдарының
интегралдарының
 болған кезде бар болуы қажет.
болған кезде бар болуы қажет.
(1) анықталған интегралды
 параметрі бойынша
параметрі бойынша
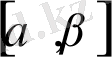 аралығында интеграл таңбасы астында интегралдау формуласы келесі түрде болады:
аралығында интеграл таңбасы астында интегралдау формуласы келесі түрде болады:
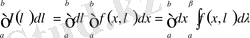 . (4)
. (4)
Интеграл астындағы функция
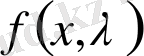 ақырлы интегралдау облысында екі айнымалының үзіліссіз функциясы болу керек. Интегралдау облысы ақырсыз болғанда қаталама меншіксіз интеграл шығады.
ақырлы интегралдау облысында екі айнымалының үзіліссіз функциясы болу керек. Интегралдау облысы ақырсыз болғанда қаталама меншіксіз интеграл шығады.
САНДЫҚ ҚАТАРЛАР
- Негізгі түсініктер мен теоремалар
Айталық
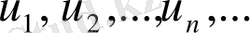 , мұнда
, мұнда
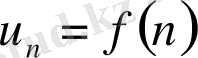 -шексіз сандық тізбек болсын.
-шексіз сандық тізбек болсын.
өрнегі
шексіз сандық қатар
деп аталады, ал
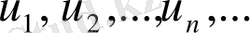 сандары қатардың
мүшелері
,
сандары қатардың
мүшелері
,
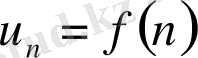 - қатардың
жалпы мүшесі
деп аталады. Қатарды көбіне
- қатардың
жалпы мүшесі
деп аталады. Қатарды көбіне
 түрінде жазады. Қатардың алғашқы
түрінде жазады. Қатардың алғашқы
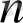 мүшесінің қосындысын қатардың
мүшесінің қосындысын қатардың
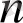 -ші дербес қосындысы
деп атайды және оны
-ші дербес қосындысы
деп атайды және оны
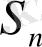 деп белгілейді.
деп белгілейді.
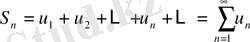
Егер қатардың
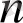 -ші дербес қосындысы
-ші дербес қосындысы
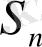
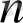 шексіз өскен кезде ақырлы шекке ұмтылатын болса, онда қатар жинақталатын қатар деп аталады, яғни
шексіз өскен кезде ақырлы шекке ұмтылатын болса, онда қатар жинақталатын қатар деп аталады, яғни
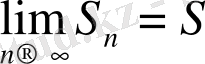
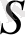 - саны қатардың
қосындысы
деп аталады. Егер
- саны қатардың
қосындысы
деп аталады. Егер
 кезде қатардың
кезде қатардың
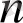 -ші дербес қосындысы ақырлы шекке ұмтылмайтын болса, онда қатар
жинақталмайды
дейді. Кез келген кемімелі геометриялық прогрессия мүшелерінен құралған
-ші дербес қосындысы ақырлы шекке ұмтылмайтын болса, онда қатар
жинақталмайды
дейді. Кез келген кемімелі геометриялық прогрессия мүшелерінен құралған
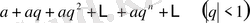
қатары
жинақталады
және оның қосындысы
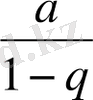 болады.
болады.
Келесі гармоникалық қатар
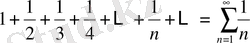 жинақталмайды.
жинақталмайды.
2. Жинақталатын сандық қатарлар туралы негізгі теоремалар
Егер
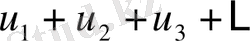 қатары жинақталса, онда осы қатардың алғашқы
қатары жинақталса, онда осы қатардың алғашқы
 мүшесін алып тастағанда қалған
мүшесін алып тастағанда қалған
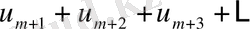 қатары да жинақталады (бұл соңғы қатарды берілген қатардың
қатары да жинақталады (бұл соңғы қатарды берілген қатардың
 -ші қалдығы деп атайды), керісінше
-ші қалдығы деп атайды), керісінше
 -ші қалдықтың жинақтылығынан берілген қатардың жинақтылығы шығады.
-ші қалдықтың жинақтылығынан берілген қатардың жинақтылығы шығады.
Егер
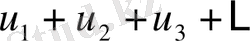 қатары жинақталатын болса және оның қосындысы
қатары жинақталатын болса және оның қосындысы
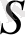 -ке тең болса, онда
-ке тең болса, онда
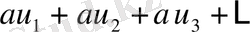 қатары да жинақталады және де бұл қатардың қосындысы
қатары да жинақталады және де бұл қатардың қосындысы
 -ке тең болады.
-ке тең болады.
Егер қосындылары сәйкес
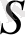 және
және
 болатын
болатын
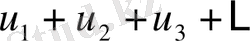 және
және
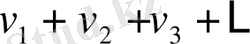 қатарлары жинақталатын болса, онда
қатарлары жинақталатын болса, онда
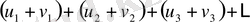 қатары да жинақталады және оның қосындысы
қатары да жинақталады және оның қосындысы
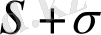 -ға тең болады.
-ға тең болады.
(қатардың жинақталуының қажетті шарты) . Егер
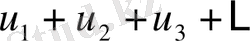 қатары жинақталатын болса, онда
қатары жинақталатын болса, онда
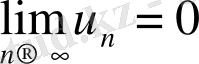 болады, яғни
болады, яғни
 кезде жинақталатын қатардың жалпы мүшесінің шегі нөлге тең болады.
кезде жинақталатын қатардың жалпы мүшесінің шегі нөлге тең болады.
Сонымен, егер
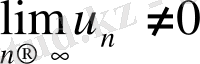 болса, онда қатар жинақталмайды.
болса, онда қатар жинақталмайды.
3. Оң мүшелі қатарлар.
Анықтама.
Егер
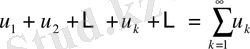 сандық қатарының мүшелері
сандық қатарының мүшелері
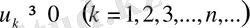 шартын қанағаттандырса, онда бұл қатар
оң мүшелі
қатар деп аталады.
шартын қанағаттандырса, онда бұл қатар
оң мүшелі
қатар деп аталады.
Оң мүшелі қатарлардың жинақталуының және жинақталмауының негізгі белгілері:
Бірінші салыстыру белгісі. Оң мүшелі екі қатар берілсін:
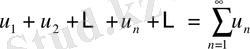 , (1)
, (1)
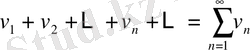 ( 2)
( 2)
және де (1) қатардың әрбір мүшесі (2) қатардың оған сәйкес мүшесінен артық болмасын, яғни
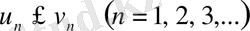 . Онда егер (2) қатар жинақталса, онда (1) қатар да жинақталады, ал егер (1. 1) қатар жинақталмайтын болса, онда (2) қатар да жинақталмайды.
. Онда егер (2) қатар жинақталса, онда (1) қатар да жинақталады, ал егер (1. 1) қатар жинақталмайтын болса, онда (2) қатар да жинақталмайды.
Екінші салыстыру белгісі.
Егер (1) және (2) қатарлардың жалпы мүшелерінің қатынасының ақырлы және нөлден өзгеше келесі
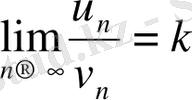 шегі бар болса, онда
шегі бар болса, онда
 және
және
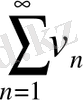 қатарлары бірдей жинақталады немесе бірдей жинақталмайды.
қатарлары бірдей жинақталады немесе бірдей жинақталмайды.
Коши белгісі.
Егер
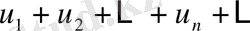 қатары үшін
қатары үшін
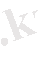
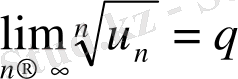 шегі бар болса, онда бұл қатар
шегі бар болса, онда бұл қатар
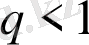 болғанда жинақталады және
болғанда жинақталады және
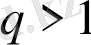 болғанда жинақталмайтын болады.
болғанда жинақталмайтын болады.
Даламбер белгісі.
Егер
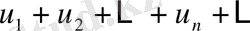 қатары үшін
қатары үшін
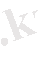
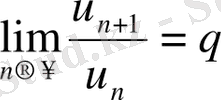 шегі бар болса, онда бұл қатар
шегі бар болса, онда бұл қатар
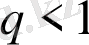 болғанда жинақталады және
болғанда жинақталады және
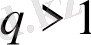 болғанда жинақталмайтын болады.
болғанда жинақталмайтын болады.
Кошидің интегралдық белгісі.
Егер
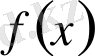 функциясы беріліп және ол
функциясы беріліп және ол
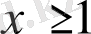 болған кезде үзіліссіз, оң және монотонды кемімелі функция болса, онда жалпы мүшесі
болған кезде үзіліссіз, оң және монотонды кемімелі функция болса, онда жалпы мүшесі
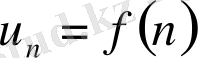 болып келген
болып келген
 қатары
қатары
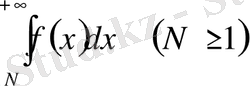 интегралы жинақталатын болса жинақталады, ал егер бұл интеграл жинақталмайтын болса жинақталмайды.
интегралы жинақталатын болса жинақталады, ал егер бұл интеграл жинақталмайтын болса жинақталмайды.
Ауыспалы таңбалы қатарлар
Анықтама. Көршілес мүшелерінің таңбалары қарама-қарсы болатын қатарлар ауыспалы таңбалы қатарлар деп аталады. Оны жалпы түрде былай жазады:
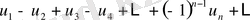 (3)
(3)
мұнда
 .
.
Лейбниц теоремасы (ауыспалы таңбалы қатарлардың жинақталу белгісі) . Егер ауыспалы таңбалы қатардың мүшелерінің абсолют шамасы монотонды кемімелі болса, ал жалпы мүшесі нөлге ұмтылса, онда бұл қатар жинақталады, яғни келесі екі шарт орындалуы керек:
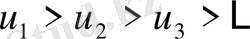 , (4)
, (4)
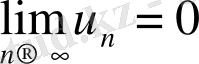 . (5)
. (5)
Салдар.
Лейбниц белгісі орындалатын жинақталатын ауыспалы таңбалы қатардың
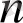 -ші дербес қосындысын алайық:
-ші дербес қосындысын алайық:
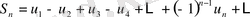
Айталық
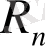 қатардың
қатардың
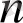 -ші қалдығы болсын. Оны қатардың қосындысы
-ші қалдығы болсын. Оны қатардың қосындысы
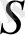 пен
пен
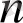 -ші дербес қосынды
-ші дербес қосынды
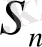 -нің айырымы түрінде жазуға болады
-нің айырымы түрінде жазуға болады
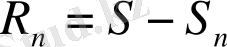 (6)
(6)
яғни
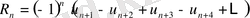 .
(7)
.
(7)
Онда ауыспалы таңбалы қатарлардың
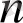 -ші қалдығының абсолют шамасы қатардың шығарып тасталған мүшелерінің біріншісінің абсолют шамасынан артық емес, яғни
-ші қалдығының абсолют шамасы қатардың шығарып тасталған мүшелерінің біріншісінің абсолют шамасынан артық емес, яғни
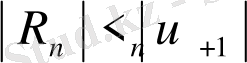 . (8)
. (8)
5. Айнымалы таңбалы қатарлар және олардың кейбір қасиеттері.
Анықтама 1. Ауыспалы таңбалы қатарлар және мүшелерінің таңбалары кез келген тәртіппен өзгеретін қатарлар айнымалы таңбалы қатарлар деп аталады.
Сонымен ауыспалы таңбалы қатарлар айнымалы таңбалы қатарлардың дербес түрі болып табылады.
Анықтама 2.
Егер келесі
 қатары, яғни айнымалы таңбалы қатардың мүшелерінің абсолют шамаларынан құрылған қатар жинақталатын болса, онда
қатары, яғни айнымалы таңбалы қатардың мүшелерінің абсолют шамаларынан құрылған қатар жинақталатын болса, онда
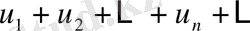 айнымалы таңбалы қатары да жинақталады. Бұл жағдайда
айнымалы таңбалы қатары да жинақталады. Бұл жағдайда
 қатары
абсолютті жинақталады
дейді.
қатары
абсолютті жинақталады
дейді.
Теорема 1.
(айнымалы таңбалы қатардың абсолют жинақталуының Коши критерийі) .
 қатары абсолютті жинақталуы үшін кез келген
қатары абсолютті жинақталуы үшін кез келген
 үшін бір
үшін бір
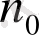 саны табылып, барлық
саны табылып, барлық
 және бүтін
және бүтін
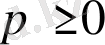 сандары үшін
сандары үшін
 теңсіздігінің орындалуы қажетті және жеткілікті.
теңсіздігінің орындалуы қажетті және жеткілікті.
Теорема 2.
Егер
 қатары абсолютті жинақталса, онда ол қатардың мүшелерінің орнын кез келген ауыстыру арқылы алынған қатар да абсолютті жинақталады және оның қосындысы берілген қатардың қосындысына тең болады.
қатары абсолютті жинақталса, онда ол қатардың мүшелерінің орнын кез келген ауыстыру арқылы алынған қатар да абсолютті жинақталады және оның қосындысы берілген қатардың қосындысына тең болады.
Қатарларды қосу және алу.
Егер айнымалы таңбалы
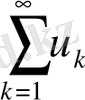 және
және
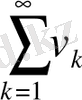 қатарлары абсолютті жинақталса, онда
қатарлары абсолютті жинақталса, онда
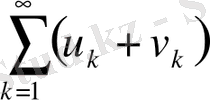 және
және
 қатарлары да абсолютті жинақталады.
қатарлары да абсолютті жинақталады.
Теорема 3.
Егер
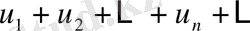 және
және
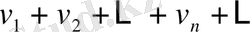 қатарлары абсолютті жинақталса және олардың қосындылары сәйкес
қатарлары абсолютті жинақталса және олардың қосындылары сәйкес
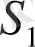 және
және
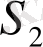 болса, онда келесі
болса, онда келесі
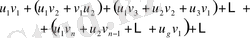
қатары да абсолютті жинақталады.
Бұл қатар берілген қатарлардың Коши бойынша көбейтіндісі деп аталады. Оның қосындысы
 болады.
болады.
Анықтама.
Егер
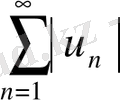 қатары жинақталмайтын болса, онда жинақталатын
қатары жинақталмайтын болса, онда жинақталатын
 қатары
шартты жинақталады
деп атайды.
қатары
шартты жинақталады
деп атайды.
Басқаша айтқанда айнымалы таңбалы қатар жинақталатын болып, ал оның абсолют шамаларынан құрылған қатар жинақталмайтын болса, онда ол қатар шартты жинақталады.
Теорема 4. Егер айнымалы таңбалы қатар абсолютті жинақталса, онда ол жәй да жинақталады.
Риман теоремасы.
Егер
 қатары шартты жинақталса, онда оның мүшелерінің орнын алмастыру жолымен
қатары шартты жинақталса, онда оның мүшелерінің орнын алмастыру жолымен
- қосындысы кез келгенсанына тең жаңа қатар құруға болады.
- жинақталмайтын жаңа қатар алуға болады.
6. Қатарлардың абсолют жинақталуының белгілері.
Теорема 1. Айталық оң мүшелі, жинақталатын
(9)
қатары және айнымалы таңбалы
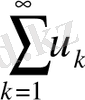 (10)
(10)
қатары берілсін. Онда, егер
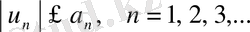 (. 11)
(. 11)
орындалса, онда (10) қатар абсолют жинақталады.
Сонымен бірге, (10) және (9) қатарлардың сәйкес қосындылары
 және
және
 үшін
үшін
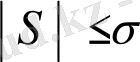 арақатынасы орындалады.
арақатынасы орындалады.
Теорема 2. Мүшелері кез келген сан болатын (10) қатар үшін
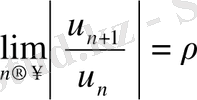 (12)
(12)
бар болса,
 болғанда (10) қатар абсолют жинақталады да,
болғанда (10) қатар абсолют жинақталады да,
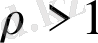 болғанда жинақталмайды.
болғанда жинақталмайды.
Теорема 3. Мүшелері кез келген сан болатын (10) қатар үшін
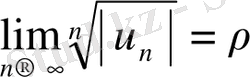 (13)
(13)
бар болса,
 болғанда (10) қатар абсолют жинақталады да,
болғанда (10) қатар абсолют жинақталады да,
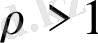 болғанда жинақталмайды.
болғанда жинақталмайды.
7. Қатарлардың абсолют және шартты жинақталуының қасиеттері.
Теорема 1. Мүшелері кез келген сан болатын
 (14)
(14)
абсолют жинақталып, оның қосындысы
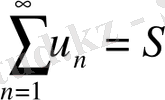 бар болса, онда (14) қатардың оң мүшелерінен құралған
бар болса, онда (14) қатардың оң мүшелерінен құралған
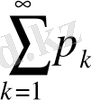 (15)
(15)
және (14) қатардың теріс мүшелерінің абсолют шамаларынан құралған
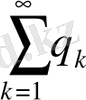 ( 16)
( 16)
қатарлары жинақталады және
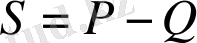 болады.
болады.
Теорема 2. Егер (14) қатар шартты жинақталса, онда (15) және (16) қатарлары жинақталмайды.
ФУНКЦИЯЛЫҚ ТІЗБЕКТЕР МЕН ҚАТАРЛАР
1. Функциялық тізбектер мен қатарлардың жинақталуы.
Айталық, қандай да бір
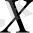 жиынында сандық мәндер қабылдайтын (жалпы жағдайда комплексті, дербес жағдайларда тек нақты)
жиынында сандық мәндер қабылдайтын (жалпы жағдайда комплексті, дербес жағдайларда тек нақты)
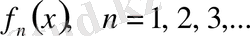 (1)
(1)
функциялар тізбегі берілсін.
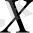 жиынының элементтерін
нүктелер
деп атаймыз.
жиынының элементтерін
нүктелер
деп атаймыз.
Егер барлық
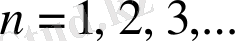 және барлық
және барлық
 нүктелері үшін
нүктелері үшін
 теңсіздігі орындалатын
теңсіздігі орындалатын
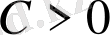 саны табылса, онда (2. 1) тізбегі
саны табылса, онда (2. 1) тізбегі
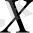 жиынында
шектелген
дейді.
жиынында
шектелген
дейді.
Егер кез келген белгіленген
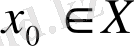 нүктесі үшін
нүктесі үшін
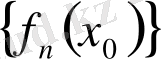 сандық тізбегі жинақталса, онда (2. 1) функциялық тізбек
сандық тізбегі жинақталса, онда (2. 1) функциялық тізбек
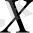 жиынында
жинақталады
дейді.
жиынында
жинақталады
дейді.
Егер (2. 1) тізбек
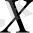 жиынында жинақталатын болса, онда әрбір
жиынында жинақталатын болса, онда әрбір
 үшін
үшін
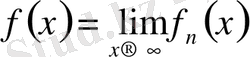
теңдігі бойынша анықталатын
 функциясы (2. 1) тізбектің
шегі
деп аталады.
функциясы (2. 1) тізбектің
шегі
деп аталады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz