Экстремумге қолданбалы есептерді шешудің геометриялық әдістері және практикалық мысалдар


«Экстремумға қолданбалы есептерді шешудің геометриялық әдістері» тақырыбында баяндама
Бағалау әдісі
Бұл әдіс экстремумге берілген алгебралық және геометриялық есептерде қолданылады.
Әдістің мәні келесідей. Белгілі бір өрнек (немесе белгілі бір F геометриялық фигурасы) қарастырылады, осы өрнекті ( немесе F фигурасын) сипаттайтын бір немесе бірнеше шамалар бөлінеді.
Бөлінген шаманы немесе шамалар жиынтығын бағалау қажет, яғни Z шамасы Z M немесе Zm ( * ) түріндегі теңсіздіктерінің бірін қанағаттандыратынын дәлелдеу қажет. Мұндағы m және M есептің шартымен анықталады. Мұнда есепті шешу үшін теңсіздіктердің біреуінің ( * ) растығын орнату қажет, яғни ( * ) біреуіне жататын әрбір Z үшін бұл өрнектің мағынасы бар (фигура бар) . Теңсіздікті қанағаттандырмайтын Z нөмірі үшін бұл өрнектің мағынасы жоқ ( Ғ фигурасы жоқ) .
Санау әдісі
Кейде аналитикалық түрде елестету қиын немесе дискретті F(x), мұндағы х С функциясын азайту мүмкін емес болған кезде табиғи түрде санау әдісі деп аталатын әдіс ұсынылады.
Бұл әдістің мәні мынада: алдымен {} С нүктелерінің тізбегі анықталады. Содан кейін F (), . . . , F () функциясының барлық мәндері кезекпен анықталады . Бұл есептеулер F( F (), (i=1. 2, . . . , n) нақты R табылғанға дейін жалғасады.
Сонда min F(x) =F () екені анық.
Жазықтықты түрлендіру әдісі
Фигуралардың үздіксіз жиынтығында қарастырылған экстремумге берілген есептерді шешудің негізгі әдісі ретінде жазықтықты түрлендіру әдісі қолданылады.
Ол келесідей:
фигурасының элементінің экстремумын табу қажет болсын, мұндағы элементтерімен анықталған.
экстремумын табу әдісі келесідей:
элементіне белгілі бір мән беріп, берілген және элементтері бойынша фигурасын құру есебін шешеміз .
Осы есепті шеше отырып, біз элементті жылжымалы деп қарастырамыз. Содан кейін жазықтықтың белгілі бір түрлендірулерін қолдана отырып, x элементі максималды немесе минималды мәнге жеткенде пайда болатын ерекшеліктерді байқаймыз.
Бұл ерекшелікті таңдау F фигурасының x элементінің экстремумы туралы қорытынды жасауға мүмкіндік береді.
Есептерді шешуге геометриялық көзқарас.
Жазықтықты түрлендіру әдісі
Геометриялық есептерді экстремумдарға шешудің негізгі әдістерінің бірі ретінде жазықтықты түрлендіру әдісі қолданылады. Әдістің мәні келесідей.
X, ai, i = 1, 2 . . . , n элементтері арқылы анықталған F фигурасының x элементінің экстремумын табу қажет болсын.
Экстремумды табу әдісі:
1) X элементіне белгілі бір мәнді береміз X = C және берілген X және ai элементтеріне сәйкес F фигурасын құру мәселесін шешіңіз.
2) Осы есепті шеше отырып, біз элементті жылжытумен қарастырамыз. Содан кейін жазықтықтың белгілі бір түрлендірулерін қолдана отырып, элемент Х максималды немесе минималды мәнге жеткенде пайда болатын ерекшеліктерді байқаймыз.
Бұл ерекшелікті анықтау F фигурасының x элементінің экстремумы туралы қорытынды жасауға мүмкіндік береді.
Нақты мәселені шешуде әдісті қолданып көрейік.
1-мысал. А негізі бар және қарама-қарсы α бұрышы бар барлық мүмкін үшбұрыштардың ішінен максималды ұзындықтағы медианасы бар үшбұрышты табыңыз.
Шешуі:

- AKAKмедианасына қарама-қарсы жатқанА=αА\ = \ \alphaберілген бұрышы құрамыз.
- Осы мәселені шеше отырып (құру әдістерін қолдана отырып) медиананың ұзындығын айнымалы деп санаймыз және медиананың максималды мәніне жеткенде пайда болатын ерекшеліктерді байқаймыз.
- Егер А нүктесі шеңбер бойымен қозғалса, онда ВС және BAC бұрышы тұрақты болып қалады және медиананың ұзындығы:А2К<AK<А1KА2К < AK < А1Kшегінде өзгереді.
- Бұл осы негізі және қарама-қарсы бұрышы бар барлық үшбұрыштардың ішінде теңбүйірлі үшбұрыштың ең үлкен медианасы бар екенін білдіреді.
2-мысал. Жазықтықта болатындай бұрыш салынған, бұрыш ішінен нүктесі белгіленген. Бұрыштың қабырғаларынан болатындай және қосындысы ең кіші мәнге ие болатындай, және нүктелерін белгілеңіз.
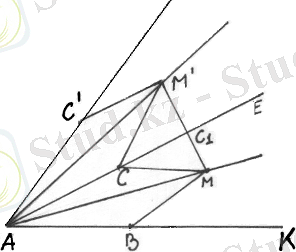
Шешуі:
Жазықтықты түрлендірудің жалпы әдістерін қолданамыз. Есептегі белгісіз элемент қосындысын береді, яғни . х элементінің сандық мәні және екі нүктесінің орындарын анықтаудаға байланысты.
Бірақ -тің шектік мәні көрінбегендітен, онда есептің шешімін бір нүктенің анықтау арқылы алу керек.
Осы мақсатпен жазықтықты нүктесінің маңайында бұрышқа айналдырамыз. В нүктесі С нүктесіне, С нүктесі С' нүктесіне, М нүктесін М' нүктесіне көшіреміз. Енді х-тің сандық мәні тек қана элементінің шектік мәнін анықтайтын С нүктесінің орнына байланысты екенін бірден байқауға болады, және егер болса, онда . Бірақ , сондықтан , мұндағы .
3-мысал. АВС үшбұрышы және оның ішінде D және Е нүктелері берілген. Үшбұрыштың әрбір қабырғаларынан өту арқылы бір нүктеден екінші нүктеге қалай ең қысқа жолмен баруға болады?
Шешуі:
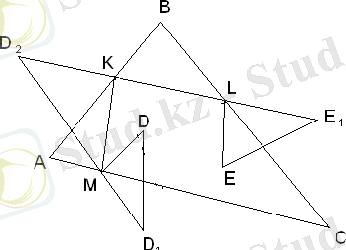
Келесі салуларды орындаймыз. D және Е нүктелеріне симметриялы болатындай етіп, және нүктелерін саламыз. Және АВ түзуіне қатысты нүктесіне симметриялы нүктесін саламыз. кесіндісін және DMKLE сынығын жүргіземіз. Оның ұзындығы кесіндісінің ұзындығына тең. D-дан Е-ге баратын кез-келген басқа жол алысырақ болатынын бірден түсінуге болады. DMKLE сияқты сынқтар үшеу. Осылардың ішінен ең қысқасын таңдап алуға болады, ол үшін сияқты үш кесіндіні өлшеп алсақ болғаны.
Теру әдісі.
Мектептегі экстремумдарға арналған геометриялық есептерді шешуде, шешімі объектілердің соңғы жиынында үлгі болып табылатын есептер бар. Бұл мәселелерді шешу әдісі әмбебап емес, өйткені ол натурал сандармен көрсетілген өлшемдері бар фигуралардың немесе фигуралардың соңғы жиынтығын қарастыратын мәселелерді шешумен байланысты. Алайда, бұл әдістің рөлі өте маңызды, ол студенттердің практикалық дағдыларын дамытады, оңтайлы модельдің оңтайлы нәтижесін табу қажеттілігін дамытады.
Ең үлкен (ең кіші) мәнді табу фигуралардың өзара орналасуына байланысты болатын мәселені қарастырыңыз.
4-мысал. Өлшемі 60x130 мм тікбұрышты материалдың парақтарынан екі типтегі бланкілерді кесіңіз, осындай мөлшерде:
Қалдықтардың минималды пайызын анықтаңыз.
Шешуі:
Бұл міндет маңызды иллюстрациялық рөл атқарады. Бұл студенттерге өндірістік материалдарды ұтымды кесу мәселесінің сипатын және оларды шешуде қажет негізгі әдістемелік әдістерді түсіндіруге мүмкіндік береді.
Жеңілдету мақсатында іздеу шешу керек ұсына оқушыларға бастапқы деректер парақтың материалдың және дайындамаларды тиісті ауқымы суретте көрсетілген. Әрі қарай, материалдың әр парағын әр түрлі жолмен кесуге болатындығын көруге болады, ал бланкілердің көп немесе аз мөлшерін алады. Мұнда материал парағын кесудің мүмкін жолдары берілген
Әрбір кесу кезінде материалдың жоғалуын әр жағдайда есептейміз. Бұл кесу нұсқаларының барлық мүмкіндіктерін қарастыруға және ең жақсысын таңдауға мүмкіндік береді. Бұл жолда сіз санау әдісімен кездесуіңіз керек. Ойлау нәтижелерін кестеге келтірген жөн, одан материалды оңтайландыру шығыны туралы қорытынды жасау оңай
Кесудің оңтайлы жоспары-материалдың 25 парағын 3 жолмен кесу керек, ал материалдың жоғалуы минималды болады, яғни 2, 6 %.
Бланкілердің санын өзгерту жеткілікті, ал тапсырма күрделене түседі, содан кейін оны студенттерге жеке жұмыс үшін ұсынуға болады.
5-мысал (ең кіші аудан туралы есеп) . Оның ішінде бұрыш пен нүкте берілген. Бұл нүкте арқылы үшбұрыштың бұрышынан ең кіші ауданды кесіп тастайтын сызық салу қажет.
Шешуі:
Ізделінді түзу мына қасиетке ие екенін көрсетеміз: оның бұрыштың ішінде жатқан кесіндісі, берілген нүктеде тең бөлінеді. Мұндай түзуді салу оңай. Мысалы, берілген М нүктесін А төбесімен қосуға болады, [AM] кесіндісінің жалғасында ұзындығы бойынша [AM] кесіндісіне тең [MA'] кесіндісін қалдыруға және А' нүктесі арқылы АС-қа параллель түзу сызуға болады. D - осы түзу пен АВ қабырғасының қиылысу нүктесі болсын. Содан кейін D нүктесін М нүктесімен байланыстыратын және E нүктесінде AC қиылысатын сызық DM = ME (үшбұрыштар үшін МDA мен МЕА тең) екенін түсіну оңай.
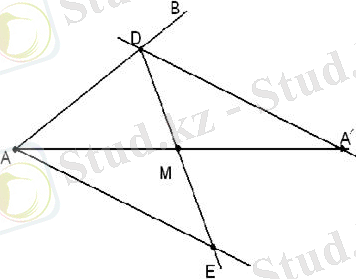
Ізделінді түзу салынды. Басқа да салу тәсілдерін қарастыруға болады.
Енді салынған түзудің ізделінді түзу екендігін дәлелдейміз.

Ол үшін тағы бір D'E' түзуін сызыңыз. Анық болу үшін Е' нүктесі Е нүктесінен тыс жатсын. Содан кейін AE'D' үшбұрышының ауданы AED үшбұрышының ауданынаY EME' үшбұрышының ауданын азайтып, MDD' үшбұрышының ауданын қосқанға тең болады. DА' түзуінің D ' E ' түзуімен қиылысу нүктесін F арқылы белгілеңіз. Содан кейін EME' және MDF үшбұрыштары тең болады. Бірақ бұл үшбұрыштардың екіншісі DD 'M үшбұрышында кездеседі, жоғарыда айтылғандардан ADE үшбұрышының ауданы AD' E ' үшбұрышының ауданынан аз болатындығы шығады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz