Математиканың ерекшелігі - оның қолданылымының әмбебаптығы

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

Баяндама

Орындаған: ммок-212, 2-топ

Ермекова Оразгүл

Еркін Фариза

Ернұр Ұлпан

Жанат Сұңқар

Ерсінқызы Мөлдір

Математиканың қолданбалы бағытын көрсету оқушылардың көзқарасын қалыптастырады. Математика сабағында теориялық материал мен есеп шығару материалын тығыз байланыстырып, оқушының нақты да жүйелі математикалық дағдысын қалыптастыру керек. Себебі бұл дағды математиканы әрі қарай меңгеруге, оны өмірде, кәсіпте қолдануға қажет болады. Мектепте оқушылар көп жағдайда абстракциялы мазмұнды есептер шығарады, балалар шартты есепке көп ынта қоймағандықтан олардың белсенділігі төмендейді. Математиканы қолданбалы бағытта оқыту дегеніміз-математиканы оқытуда техника мен оған жақын ғылымдарда оны қолдану, халық шаруашылығы мен тұрмыста қолдануға бағыттау, немесе оқытуға политехникалық бағыт беру, яғни физика, химия, география, сызу, технология сабақтарымен байланыс орнату; компьютерлік сауаттандыру, математикалық ойлау және жұмыс дағысын қалыптастыру, оқушыны есептер шешуге, мысалдар шығартуға, оқушы өз бетінше есептей білу дағдыларын қалыптастыру.

Математиканың ерекшелігі - оның қолданылымының әмбебаптығы. Міне, осы кезде математиканың табиғаттағы, адам өміріндегі рөлі айқындалады. Мектепте математика курсын оқытудың ең маңызды мақсаттарының бірі-математиканың қолданбалы мүмкіндіктерін ашу. Ал бұл мүмкіндікті ашуда қолданбалы есептердің маңызы зор. Қолданбалы есептер деп математикалық әдістермен шығарылатын математикадан тыс құрылған есептерді айтамыз. Қолданбалы есептерде мынандай талаптар болуы керек:математикалық және математикалық емес проблемалар көрініс табуы керек, бағдарламаға сай болуы, есеп мазмұны нақтылыққа құрылған, шығарылу жолы практикалық әдіс тәсілдерге жақын болуы керек. Кейбір жағдайларда қолданбалы есептерді шығару барысында көптеген мұғалімдер ол есептердің математикалық модулін құруға, мысалы теңдеу құруға, оны шешуге көбірек назар аударады. Әрине бұл дұрыс, бірақта мұндай есептерді шығару сан жағынан аз болса да, ол есептердің бастапқы берілген шарттарын жан-жақты талқылауға, оларда берілген шамалардың мән мағынасын анықтауға, сондай-ақ, ол есепті шешудің таңдап алынған жолдың дұрыстығын анықтап, талдауға аса назар аудару қажет, өйткені қолданбалы есептерді шығару барысында бұл мәселе оқушыларда үлкен қиындық тудырады. Және де оқушыларда кәсіпке байланысты қолданбалы бағыттағы ойлауды қалыптастыруға үлкен әсерін тигізеді. Мектептің математика курсының құрамына математикалық анализ бастамаларын енгізу, оның қолданбалылығын және өмірмен байланыстылығын күшейтуге үлкен әсер етеді. Бірақта ол мүмкіндіктерді жүзеге асырып оқушыларды математикалық анализ әдістерін қолданбалы есептерді шығаруға пайдалануға дағдыландыру төмен жағдайда болып отыр. Оның бірінші себебі дифференциалдау интегралдау амалдары мектеп курсында кештеу (10-11сыныптарда) енгізілген. Екінші себебі математикалық анализдің тәсілдерін қолданып қолданбалы есептерді шығаруға үйрететін әдістемелік құралдар жоқтың қасында, сонымен қатар, мұндай есептер мектеп оқулықтарында өте аз. Ең негізгі себебі мұғалімдер көпшілігінің математиканы оқытудың қолданбалылығы мен политехникалық бағыттылығын арттыруға немқұрайлы қарауы болып табылады.

Экстремумға берілген есептер әлі күнге дейін бір жүйеге келтірілмеген, ондай есептерді шығарудың әдістемесі жасалып, бір ізге түсірілмеген. Қазіргі таңда экстремумға берілген есептермен мектеп оқушылары тек 10-11 сыныптарда туынды тақырыбын өту кезінде ғана танысады.

Экстремумға берілген көп есептер туындының көмегімен шығарылады, алайда оларды элементар әдістермен де шығаруға болады. Ондай әдістермен негізгі мектеп оқушыларын таныстырып, есептер шығарып жаттықтыратын болсақ, оқушылар жоғары сыныптарда өтілетін экстремум ұғымымен ертерек танысып, жоғары сыныпта ол тақырыпты өту барысында еш қиындықсыз оңай меңгеруіне және де күнделікті өмірде кездесетін экстремумға берілген есептерді шығара алуына үлкен көмек болар еді.

Сызу пәнінің мұғалімі резервуар сызумен таныстырады. Оқушылар өздерін толғандырған сұрақтарын қояды.

Шешуі:

Іщкі цилиндрдің табанының радиусы x, ал биіктігін h деп белгілейік. Сыйымдылығы V0 науаның табаны мен қабырғасына жұмсалатын материал барынша аз болу үшін ішкі цилиндрдің табанының радиусы мен биіктігінің қандай қатынаста болу керек екенін табайық. Науаның табаны мен қабырғасына кететін материалдың көлемі

$V = (x + d) ^{2}(h + d) - xh^{2}$

формуласымен анықталады. Осы функцияның ең кіші мәнін анықтау қажет. Сонда V көлемінің тәуелсіз х пен h айнымалыларының функциясы болатынын аңғару қиын емес.
Сонымен ішкі цилиндрдің табанының радиусы мен биіктігі өзара тең болғанда ана сыйымдылығы белгілі науаны жасауға барынша аз материал жұмсалады.

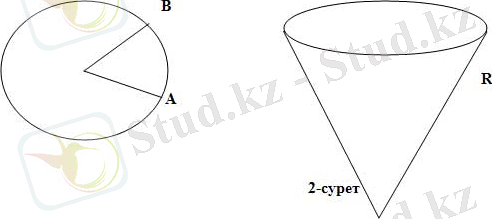
2- мысал. Химиялық лабораторияларда қолданылатын конус тәрізді дөңгелек фильтр(сүзгі) қағазды орау арқылы жасалады. АОВ секторынан басқа дөңгелектің қалған бөлігі конустық воронканың бүйір қабырғасын құрайтындай етіп оралады. . Сүзгі қағаздың радиусы R болса, табаны қандай болғанда конустың сыйымдылығы үлкен болады? Шешуі: х арқылы конустың табанының радиусын белгілейміз. 0<x

4erzg

3- мысал

Өлшемі 5см $\times$ 8см тік төртбұрыштың төрт бұрышынан өлшемдері бірдей квадратты қиып алып, одан беті ашық қорап жасау керек. Онда қораптың ең үлкен көлемін анықтаңыз :

V=a*b*c =(8-2x) (5-2x) x = (40 - 26x+4 $x^{2}$ ) x = 4 $x^{3}$ - 26 $x^{2}$ +40x

Сонда х айнымалысына байланысты құрылған функция:

4 $x^{3}$ - 26 $x^{2}$ +40x Сонда х $\in$ (0. 2, 5)

Кризистік нүктені табамыз:

V’ = 12 $x^{2}$ -52x+40 =0 /4

3 $x^{2}$ -13x+10 =0

$x_{1} = 1$ х $\in$ (0. 2, 5)

$x_{2} = \ \frac{10}{3}$ $\varnothing$

$x_{1} = 1$ Нүктесі функцияның ең үлкен мәнге ие екенін анықтаймыз. Екінші реттік туынды аламыз.

V’’=24x-52 = 24-52 = -28 < 0 Функция осы нүктеде максимум мәнді қабылдайды.

$f_{\max}$ => $f_{е. ү}$

V = 6*3*1 =18 ${см}^{3}$

4-мысал

Өлшемдері 60 см×60 см болатын шаршы формалы картон парағы бар. Картонның бұрыштарындағы квадраттарды кесіп тастағанда, картоннан төбесі ашық қорап алуға болады. Қораптың көлемі ең үлкен болуы үшін қандай өлшемді квадраттарды кесу керек?

Кесілген шаршының ұзындығын - х (см) деп белгілейік. Онда қалған бөліктің ұзындығы: 60-2х (см)

$V = (60 - 2x) (60 - 2x) x = x(60 - 2x) ^{2}$

$V(x) = 4x^{3} - 240x^{2} + 3600x$

$V'(x) = 12x^{2} - 480x + 3600$

$V'(x) = 0$

$x^{2} - 40x + 300 = 0$

$x_{1} = 30; \ болмайды\$

$x_{2} = 10$

Жауабы: 10см×10см

5-мысал

Периметрі 20 м болатын тік төртбұрыш формалы бөлменің ауданы ең үлкен болатындай бөлменің ені мен ұзындығын табыңыз:

Ені мен ұзындығын бір айнымалы арқылы өрнектейміз:

а, 10-а

S = a*(10-a) = 10a - $a^{2}$ Бұл - мәтінге байланысты құрылған функция.

a $\in$ (0. 10)

Функцияның ең үлкен және ең кіші мәнін табу үшін кризистік нүктелерін табамыз.

$S^{1}$ = 10-2a = 0

a=5

Тік төртбұрыштың ұзындығы болатын а - ның қандай да бір мәні a=5; Осы мән тіктөртбұрышты ең үлкен мәнге жеткізетін мән болатынын тексеруіміз керек.

5 $\in$ (0. 10)

Берілген аралықта бір ғана не максимум, не минимум нүкте бар. Соны анықтауымыз керек. Ол үшін екінші ретті туынды аламыз:

$S^{11}$ =-2 <0 $f_{\max}$ => $f_{е. ү}$

Ұзындығы: 5м

Ені: 10-а = 10 - 5 = 5 м

Қорытынды:

1. ) ойлау, есептеу дағдысы қалыптасты.

2. ) мұнай құбырларының сыйымдылықтары интегралдың көмегімен анықталды.

3. ) ғылыми әрі практикалық көзқарастары ұштасты.

Қазіргі кезде ғылымның барлық дерлік салаларында математикалық әдістерді қолдану қажетті шартқа айналды. Ол өмір талабынан, ғылыми - техникалық прогресттің дамуынан туындайды. Қолданбалы есептерді түсініп шығарудың бір шарты пәнаралық байланысты жүзеге асыру. Физикалық, химиялық немесе географиялық т. т. мазмұнды есептерді шешу барысында, атап айтқанда, 6-сыныпта масштабты, пропорцияны өткенде, жол, уақыт, жылдамдыққа берілген есептерді шешуде, оқушылар математикалық ұғымдар мен заңдылықтарды терең түсініп, сонымен қатар мамандыққа даярлықтың негіздерін меңгереді. ҰБТ-ға дайындауда химияға қатысты, концентрация мен қоспаға байланысты есептер көптеп кездеседі. Бұл есептерге тәжірибелік және математикалық сипаттағы математикалық әдісті пайдаланамын. Қолданбалы есептерді шығару оқушылардың басқа пәндерді оқып білуіне, еңбек барысында, күнделікті өмірде математиканы қолдана білуге қажетті білімдер, іскерліктермен дағдыларды қалыптастыруға септігін тигізеді, математикалық олимпиадаларға дайындығын ұштайды. Ең негізгісі қолданбалы есептер арқылы білімін тереңдетіп, кәсіптік бағдар береміз. Қорытынды. Кәсіби бағдар беруде қолданбалы курстардағы қолданбалы есептердің маңыздылығы мынада: Оқушының өз білімін практикамен ұштастыруы жүзеге асады. Белгілі бір дәрежеде ғылыми тұжырымды пайдалана отырып оның математикалық әдісті қолдана отырып, нақты өмірде қолдана білуге үйренеді. Күрделіден жеңілге қарай принципімен білімнің мағынасы ашылады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.