Экстремалды есептер және оңтайландыру әдістері: мектепте оқыту мен практикалық қолдану


Баяндама
Орындаған: ммок-212, 2-топ
Ермекова Оразгүл
Еркін Фариза
Ернұр Ұлпан
Жанат Сұңқар
Ерсінқызы Мөлдір
Қазіргі уақытта ғылым мен техниканың көптеген салаларының дамуының табыстылығы негізінен математиканың әртүрлі салаларының дамуына байланысты екендігі жалпыға бірдей мойындалды. Мұндай салаларға, мысалы, ықтималдықтар теориясы, сызықтық және динамикалық бағдарламалау, оңтайлы басқару теориясы, математикалық экономика және т. б. жатады. Математика өндірісті ұйымдастыру мәселелерін шешудің, оңтайлы шешімдерді іздеудің құралына айналады және, сайып келгенде, еңбек өнімділігін арттыруға және ұлттық экономиканың тұрақты прогрессивті дамуы. экономика. Өндірістің тиімділігін арттырудың және өнім сапасын арттырудың маңызды шарты математикалық әдістерді технология мен халық шаруашылығына кеңінен енгізу болып табылады, ол алға қойылған әртүрлі мәселелерді шешуге мүмкіндік беретін сапалы және сандық зерттеулердің жаңа, тиімді әдістерін құруды көздейді. тәжірибе арқылы.
Қазіргі студенттер орта мектепте «тиімділік», «оңтайлылық», «экстремум», «ең үлкен», «ең кіші», «ең жақсы», «ең тиімді» сияқты өнеркәсіп пен ғылымның дамуына қатысты маңызды ұғымдар туралы түсінік ала алады. , «ең үнемді» және т. б. Бұл, ең алдымен, адамдардың еңбек қызметі процесінде материалдық және еңбек ресурстарын тиімді пайдалануға және өндірістің берілген көлемімен шығындарды азайтуға (минимизациялауға) немесе, берілген ресурстармен максималды өнімді қамтамасыз ету. Осымен қатар білім берудегі заманауи көзқарас математиканы оқытудың қолданбалы аспектілеріне ерекше назар аударуды қажет етеді. Оңтайландыру есептерін шығаратын математика есептерінің ішінде мектеп математика курсында жиі кездесетін және өз кезегінде жалпы оңтайландыру есептерін қарастыруға негіз болатын экстремумдар мен оптимумдарға арналған есептерді бөліп көрсету қажет.
Егер F(u) сандық функциясы үздіксіз болса, U бойынша F(u) экстремумына F'(u) = 0 немесе F'( u ∈ U нүктелерінде ғана жетуге болатыны математикалық талдаудан белгілі. u) U жиыны үшін де жоқ немесе шекара болып табылады. Экстремумды табудың сипатталған әдісін X класынан бастап есептердің шешімі оның туындысымен бірге функцияны зерттеуге дейін қысқартылған барлық жағдайларда қолдануға болады. , жеткілікті қарапайым пішіні бар. Көптеген практикалық есептерде туындыны есептеу қиынға соғады және көбінесе туындының бізді қызықтыратын нүктелерде бар-жоғы белгісіз. F(u) функциясы тек кесте түрінде беріледі немесе мәселені аналитикалық түрде беру әдетте қиынға соғады. Туынды әлі де есептелетін жағдайларда F'(u) = 0 теңдеуінің шешімі де күрделі қиындықтарға әкелуі мүмкін.
Туындыны есептеуді қажет етпейтін экстремалды есептерді шешудің әдіснамалық техникасы, жолдары болуы маңызды. Бұл, мысалы, дискретті оңтайландыру есептерін шешу кезінде орын алады. Экстремалды есептердің ерекше түрі туындының көмегінсіз шешілетін сызықтық программалау есептері болып табылады. Туынды көптеген геометриялық есептерді шешуде де қолданылмайды.
Білім беруде экстремалды тапсырмаларды енгізу педагогикалық тұрғыдан негізделген, өйткені олар оқушылардың санасында адамның қалай ізденетіні, өмірлік мәселелердің шешіміне үнемі қол жеткізетіндігі, соның арқасында оның қызметінің нәтижесі мүмкіндігінше жақсы болатыны туралы түсінік қалыптастырады. Осы типтегі есептерді шығара отырып, студенттер, бір жағынан, математикалық ұғымдардың абстрактілі сипатын, екінші жағынан, олардың практикалық, өмірлік есептерді шешуге үлкен және тиімді қолданылуын көреді. Экстремалды есептерді мұндай тұжырымдау оқу материалын қолдану аясының кеңеюіне ықпал етеді, мектеп оқушыларына математикалық білім берудің терең мақсаты - математиканы адам іс-әрекетінің әртүрлі салаларында қолдануды үйретуде бұл міндеттердің рөлін арттырады. .
Экстремалды тапсырмалар оқушыға жұмыста, қоршаған шындықты білуде жиі қолданылатын мектеп математика курсының кейбір идеяларымен және қолданбалы әдістерімен танысуға көмектеседі. Мұндай тапсырмалар оқу материалының мазмұнына, зерттелетін теорияның практикада қолдану аспектілеріне елеулі әсер етуі мүмкін. Мектепте, математика сабақтарында мен қарапайымырақ мақсат қойдым: оқушыларды мәнді экстремалды есептердің мысалдары бойынша тәрбиелеу, оларда ғылыми дүниетанымды, табиғатта да, қоғамдық өмірде болып жатқан процестерге терең көзқарасты қалыптастыру, математикалық білімнің маңыздылығы мен есептерді шығара білу.
Экстремалды есептерді шешу оқушылардың математикалық білімдерін тереңдетіп, байытуға ықпал етеді. Есептер арқылы олар үзіліссіз дискретті жиында қарастырылатын зерттелетін функциялардың экстремалды қасиеттерімен, теңсіздіктердің кейбір қасиеттерімен танысады. Белгілі бір геометриялық фигураның қасиеттерін зерттей отырып, оқушылар тапсырмалардың көмегімен осы фигураның экстремалды қасиеттері туралы білім алады, сонымен қатар қолданбалы есептерді шешуде оларды қолдану жолдарын меңгереді. баға жетпес маңыздылығы Мектептегі математика курсында экстремалды есептер шығаруды оқушылардың зерттеушілік мәдениетін дамытуда да көремін. Өйткені, мұндай есептердің барлық шешімдері математикалық модельді зерттеу деңгейінде және оңтайландыру құралдарын пайдалану арқылы нақты жағдайды зерттеу деңгейінде ұсынылады. Сонымен қатар, экстремалды есептердің көпшілігін шешу процесінде эвристикалық әдістер кеңінен және сәтті қолданылады, олар алгоритмдік әдістерден айырмашылығы, ұсынылған есептерді шешудің жолын ұсына алады.
Экстремалды мәселелерді шешу үшін келесі әдістер бар:
1. Қолдау функциясы әдісі;
2. Бағалау әдісі;
3. санау әдісі;
4. Жазықтықты түрлендіру әдісі.
Функцияның экстремумы - берілген жиындағы функцияның ең үлкен (ең кіші) мәні. Экстремумға жеткен нүкте экстремум нүктесі деп аталады.
Туынды нөлге тең нүктелер стационарлық нүктелер деп аталады.
Функция үздіксіз және оның туындысы жойылатын немесе жоқ болатын нүктелер критикалық нүктелер деп аталады.
Функцияның экстремумын табу тәуелсіз тапсырма да, функцияны толық зерттеу және оның графигін салу кезеңдерінің бірі де болуы мүмкін.
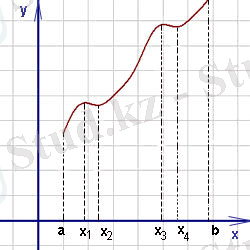
Экстремалды нүктелер максималды және минималды нүктелер үшін біріктіруші термин болып табылады және осы нүктелердегі функциялардың мәндері функцияның экстремумдары деп аталады.
Үздіксіз функцияның графигін қарастырайық. 1-суретте функцияның нүктесіндегі мәні оған жеткілікті жақын, оң және сол жақтағы оған іргелес нүктелердегі функция мәндерінен аз екендігі көрсетілген. Бұл жағдайда функцияның нүктесінде минимумы бар деп айтылады.
нүктесінде функцияның мәні оның оң және сол жағында орналасқан оған жеткілікті жақын нүктелердегі функция мәндерінен үлкен. Бұл жағдайда функция нүктесінде максимумға ие деп айтылады.
Экстремум нүктелеріне қатаң анықтамалар берейік.
1-анықтама: f(x) функциясының нүктесінде минимумы бар, егер нүктесінің осы маңайындағы барлық x≠ үшін f( ) <f( ) +∆x) теңсіздігі болатын көршілестігі бар болса. қанағаттандырады.
2-анықтама: f(x) функциясының нүктесінде максимумы бар, егер нүктесінің осы маңайындағы барлық x≠ үшін f( ) >f( ) +∆x) теңсіздігі болатын көршілестігі бар болса қанағаттандырады.
Жоғарыда келтірілген анықтамалардан функцияның экстремумының жергілікті сипатқа ие екендігі шығады - бұл жақын мәндермен салыстырғанда функцияның ең үлкен және ең кіші мәні. Интервалда функцияның бірнеше экстремумдары болуы мүмкін және функцияның кез келген минимумы оның максимумдарының кез келгенінен үлкен болып шығуы мүмкін.
Мысал. Берілген тікбұрышты парақтан ең аз қалдықпен кесуге болатын құмыраның оңтайлы өлшемдерін табыңыз.
біз цилиндрдің s(r) радиусына байланысты оның жалпы бетінің ауданының функциясын құрамыз. Құты түбінің (және қақпағының) радиусы r см болсын:
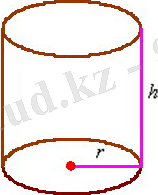
Содан кейін төменгі аймақ
Шарт бойынша банканың көлемі
... жалғасы
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz