Теңдеулер мен теңсіздіктерді шешуге үйрету

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 26 бет
Таңдаулыға:

6-лекция
Теңдеулер мен теңсіздіктерді шешуге үйрету.
Жоспары
1.Мектеп математика курсында теңдеулер мен теңсіздіктер тақырыбын оқыту реті.
21.Теңдеу және теңсіздік ұғымдары. Мүмкін мәндер облысы.
3. Мәндес теңдеулер мен теңсіздіктер.
4.Теңдеулер мен теңсіздіктерді шешудің жалпы әдістері.
Әдебиеттер:
1. Рахымбек Д. Арифметика, алгебра, анализ бастамаларын оқыту әдістемесі. Оқулық - Шымкент: М. Әуезов атындағы ОҚМУ баспа орталығы 2016. - 432 б
2. Елубаев С. Математиканы оқыту әдістемесі. - Алматы; Эверо, 2016
3. Мектеп оқулықтары
4. Мұғалімге арналған оқу-әдістемелік құралдар

1. Мектептегі теңдеуді шешу туралы жалпы мәлімет
Мектепте теңдеу мен теңсiздiктi және олардың жүйелерiн ерте бастан жүйелi түрде оқыту дәстүрi қалыптасты. Бұл дәстүр қазiргi бағдарламаларда да көрiнiс тапқан: теңдеу ұғымы, сызықтық теңдеу, екi белгiсiзi бар сызықтық теңдеулер жүйесi 6-сыныпта, квадрат теңдеулер мен рационал теңдеулер 7,8-сыныпта, мәндес теңдеулер мен теңсiздiктер және тригонометриялық теңдеулер 10-сыныпта, дифференциалдық теңдеулер туралы ұғым, көрсеткiштiк және логарифмдiк теңдеулер 11-сыныпта оқытылады.
Орта мектепте теңдеулер мен теңсiздiктердi оқып-үйренудің әртүрлi нұсқаулары бар‚ кейде теңдеулер мен теңсiздiктердi параллель оқыту туралы ұсыныс та жасалынып жатады.
Әдiстемелiк әдебиеттерде теңдеудiң мынадай анықтамалары кездеседi.
1. Екi алгебралық өрнекке енетiн әрiптiң қандай да бiр мәндерiнде бiрдей сандық мәндер қабылдайтын теңдiктi теңдеу деп атайды.
2. Бiр белгiсiзi бар теңдеу былайша жазылады: f(х)=(х). Егер х0 саны бiрiншiден f(х) және (х) функцияларының анықталу облысына енетiн болса, екiншiден мына сандық теңдiк f(х0)=(х0) орындалатын болса, онда х0 саны теңдеудiң түбiрi деп аталады. Теңдеудi шешу деп оның барлық түбiрлерiн табуды айтады.
3. Бiр айнымалысы бар теңдеу деп осы айнымалы арқылы құрылған теңдiктi айтады. Теңдiктегi айнымалыны әдетте белгiсiз шама дейді. Белгiсiздiң орнына апарып қойғанда берiлген теңдеудi дұрыс теңдiкке айналдыратын айнымалының мәнiн теңдеудiң түбiрi (шешiмi) деп атайды.
4. Белгiсiзi бар теңдiктi теңдеу деп атайды. Белгiсiздiң теңдiктi дұрыс сандық теңдiкке айналдыратын мәндерi теңдеудiң түбiрi деп аталады. Теңдеудi шешу дегеніміз оның барлық түбiрлерiн табу.
Теңдеу ұғымының бұл анықтамаларын бiр-бiрiне қарсы қоюға болмайды. Бұл анықтамалардың әрқайсысы теңдеулердi шешудiң теориялық және практикалық мәселелерiнде қолданылады.
Мектеп оқулықтарында қазiргi кезде теңдеудiң анықтау 4-анықтама негiзiнде алынған.
Теңдеу ұғымына ең жақын ұғым теңбе-теңдiк. Бiрақ ол көбiнесе теңдеу ұғымына байланыссыз анықталады. Бұл әдетте теңбе-теңдiк теңдеуден бұрын өтiлген жағдайда кездеседi. Алдымен теңбе-теңдiк айнымалының кез келген мәнiнде дұрыс болатын теңдiк деп қарастырылады. Кейiнiрек рационал бөлшектердi қарастырғанда теңбе-теңдiк ұғымы дәлiрек анықталады: айнымалының барлық мүмкiн мәндерiнде орындалатын теңдiктi теңбе-теңдiк деп атайды.
Теңдеу мен теңбе-теңдiк ұғымдарының арасыңдағы тiкелей байланыс мынадай анықтамамен берiледi: егер f(х)=g(х) теңдеуiнiң шешiмдерiнiң жиыны берiлген теңдеудiң аңықталу облысымен сәйкес келетiн болса, онда бұл теңдеудi теңбе-теңдiк деп атайды.

2. Мектептегi теңдеулерді шешудің жалпы мәселелері

Орта мектепте теңдеулер тақырыбына байланысты мынадай негiзгi мәселелер қарастырылады.
Бiр немесе бiрнеше белгiсiзi бар теңдiктi теңдеу деп атайды. Бiр белгiсiзi және n белгiсiзi бар теңдеу жалпы түрде былайша жазылады:
f(x)=0; f(x1, x2, ... ..xn)=0.
f(x) немесе f(x1, x2,...,xn) функцияларының анықталу облысын теңдеудiң мүмкiн мәндер облысы дейді.
Мысалы: теңдеуiнiң мүмкiн мәндерiнiң облысы болады.
Орнына апарып қойғанда берiлген теңдiктi дұрыс санды теңдiкке айналдыратын белгiсiздiң мәндерiн теңдеудiң түбiрлерi деп атайды.
Мысалы: х2 - 4=0 теңдеуiн шешу деп, оның түбiрлерi х1 = -2, х2 = 2-нi табуды айтады. х2 + 4=0 теңдеуiн шешу деп, оның түбiрлерiнiң жоқ екендiгiн көрсету.
Кез келген күрделі теңдеу түрлендірулер нәтижесінде не сызықтық, не квадрат теңдеуге, не қарапайым иррационал, тригонометриялық, көрсеткіштік, логарифмдік теңдеулердің біріне келтіріледі.
Рационал, иррационал, көрсеткіштік т.б. теңдеулердің белгілі бір түріне лайықты өзіндік шешу әдістері болғанымен, барлық теңдеулерді шешуге ортақ идея, жалпы әдістер бар. Ондай жалпы әдістер үшеу:
1) Теңдулерді шешудің көбейткіштерге жіктеу әдісі;
2) Теңдулерді шешудің жаңа белгісіз енгізу әдісі;
3) Теңдулерді шешудің функционалды-грфиктік әдісі.

3.Теңдеулерді шешудің көбейткіштерге жіктеу әдісі
Көбейткіштерге жіктеу әдісінің мәні мынада: f(x) = 0 теңдеуін шешу керек, мұндағы f(x) = болсын. Сонда f(x)=0 теңдеуін, оған қарағанда қарапайым теңдеулер жиынтығымен (бірлігімен) алмастыруға болады. Осы теңдеулер жиынтығының түбірлерін тауып, олардың ішінен f(x)= 0 теңдеуінің анықталу облысына тиістілерін таңдап алсақ, онда f(x) = 0 теңдеуінің түбірлерін табамыз.
Демек f(x) = 0 теңдеуін шешу үшін теңдіктің сол жағын көбейткіштерге жіктеп алуымыз керек. f(x) өрнегін көбейткіштерге жіктеудің мектеп математика курсында мынадай тәсілдері оқып-үйреніледі:
1) топтау және ортақ көбейткішті жақша сыртына шығару;
2) қысқаша көбейту формулаларын пайдалану (мәселен а 2 - в2 = (а - в) (а + в));
3) квадрат үшмүшелікті көбейткіштерге жіктеу: , мұндағы квадрат үшмүшеліктің түбірлері.
1-мысал. 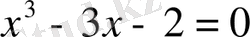теңдеуін шешу керек.
Ш е ш у і. деп алайық, сонда:

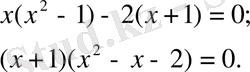
1. x+1=0, х1= -1.
2. х2 - х -1 = 0 бұдан х2= -1, х = 2.
Жауабы: -1; 2.
2-мысал. Теңдеуді шешу керек:

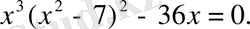
Ш е ш у і: Теңдеудің сол жағын алдымен қысқаша көбейту формуласын пайдаланып, кейін топтау және ортақ көбейткішті жақша сыртына шығару тәсілімен көбейткіштерге жіктейміз.
.
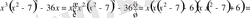
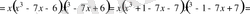
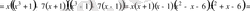
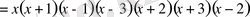х(х+1)(x-1)(x-3)(x+2)(x+3)(x-2)=0
Бұдан
Жауабы: 0;
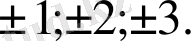
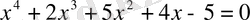
3-мысал.теңдеуін шешу керек.
Ш е ш у і: Теңдеудің сол жағындағы 5х2 = х2 + 4х2 түрінде жазып алғаннан кейін, топтап, квадрат үшүшелікті көбейткіштерге жіктейміз:

Енді 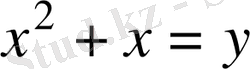деп алмастыру жасасақ 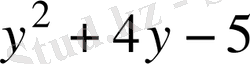квадрат үшмүшелігін аламыз. Үшмүшеліктің түбірлері 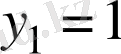және Сонда 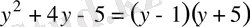болады. Бұдан
= 0 болып жіктеледі.
Әрбір көбейткішті жеке-жеке нөлге теңеп берілген теңдеудің түбірлері табылады .
Бірінші теңдеудің түбірлері ,
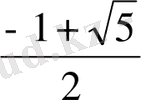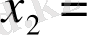
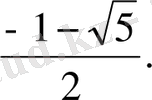
Екінші теңдеудің нақты сандар жиынында шешімі жоқ.
Жауабы: ;
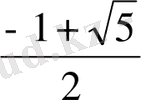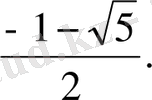
Бүтін коэффициенті рационал көпмүшелікті көбейткіштерге жіктеуде бос мүшенің бөлгіштерін ескеретін арнайы тәсіл бар.
Теорема. Егер бүтін коэффициенті р(x) көпмүшелігінің бүтін түбірі 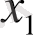болса, онда 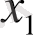саны көпмүшеліктің бос мүшесінің бөлінгіші болады.
Осы теореманың негізінде көпмүшеліктерді көбейткіштерге жіктеу әдісін пайдаланып бүтін коффициентті р(x)=0 теңдеуі мынадай ретпен шығарылады:
1. р(x) көпмүшелігінің бос мүшесінің барлық бөлгіштері жазылады.
2. Бөлгіштердің арасынан р(x) көпмүшелігінің түбірі болатыны саны таңдап алынады.
3. р(x) көпмүшелігі көбейткіштерге (х - ) екімүшелігі болатындай етіп жіктеледі.
4. р(x)=0 теңдеуін (х-)g(x) = 0 теңдеуіне түрлендіріп алғаннан кейін g(x) = 0 теңдеуін шешуге көшеді.
4-мысал. 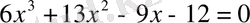теңдеуін шешу керек.
Шешуі.1. Бос мүшенің бөлгіштерін жазып шығамыз, яғни
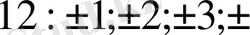
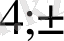
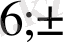-12.
2. мәндерін ретімен қойып р() есептейміз;

Демек, 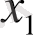= - 3.
3. Берілген теңдеудің оң жағындағы көпмүшеліктің көбейткіштерге жіктелуінде (х+3) екімүшелігі болатындай етіп таңдап аламыз.

=
=
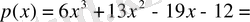
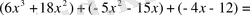
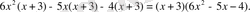
4. Берілген теңдеу мына түрге келеді

бұдан,
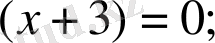
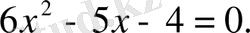
Бірінші теңдеуден 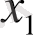= 3, екіншіден
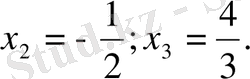
Жауабы:
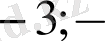
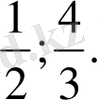
3-жағдайда көпмүшелігін (х+3) екімүшелігіне бұрыштап бөлу арқылы да көбейткіштерге жіктеуге болады.
4. Теңдеулерді шешудің жаңа айнымалы енгізу әдісі
f(x) = 0 теңдеуін р(g(x)) = 0 түріндегі теңдеуге түрлендіру мүмкін болса, онда u = g(x) айнымалысын енгізіп, p(u) = 0 теңдеуін шешеді. Егер p(u) = 0 теңдеуінің түбірлері 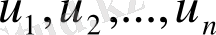болса, онда 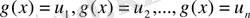теңдеулер жиынтығының шешімдері берілген теңдеудің түбірлері болады.
Жаңа айнымалыны енгізу теңдеуді шешуді әлдеқайда оңайлатады. Сондықтан теңдеуді шешу үшін жаңа айнымалыны дұрыс таңдай алу, мектеп оқушыларының математикалық мәдениетінің маңызды құрамды бөлігі болып саналады.
Оқушыларды теңдеуді шешу үшін оны бірден түрлендіруге асықпастан, қандай жаңа айнымалы енгізсек есептің шығарылуы оңайлауы мүмкін деп ойлануға үйрету керек. Егер теңдеудің шартынан жаңа айнымалыны енгізу бірден белгілі бола қоймаса, онда қандай түрлендірулер жасасақ жаңа айнымалыны енгізу мүмкіндігі бар деп ойлану керек.
Сондықтан жаңа айнымалыны енгізу бірден теңдеуді шешуге кірісу кезінде, немесе біршама түрлендірулерден кейін көрінуі де мүмкін, кейде бір емес, екі жаңа айнымалы енгізуге тура келетін жағдайлар да кездеседі.
1-мысал.Теңдеуді шешу керек

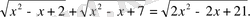
Ш е ш у і. 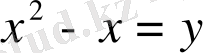де белгілесек берілген теңдеу мынадай түрге келеді:

Енді 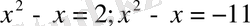теңдеулерін шешу қалды.
Бірінші теңдеудің түбірлері 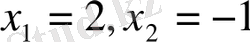, ал екінші теңдеудің түбірлері жоқ.
Жауабы: 2; - 1.
Бұл теңдеуді шешу үшін 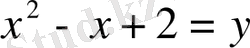деп белгілеуге де болады.
2-мысал. 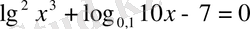теңдеуін шешу керек.
Ш е ш у і. Теңдеудегі қосылғыштарды жеке-жеке түрлендірейік:

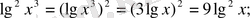
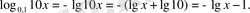
Сонда берілген теңдеу мына түрде жазылады:
.
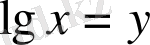деп белгілесек, 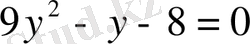болады. Бұдан
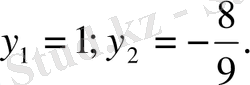
Енді мынадай екі теңдеуді шешеміз:
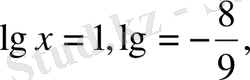бұдан .
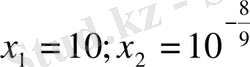Жауабы:
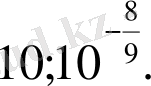
3-мысал. Теңдеуді шешу керек:.
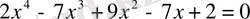Ш е ш у і. Теңдеуді шешу үшін қандай белгісіз енгізу керек екені белгісіз. Бірақ, мұндай теңдеулердің өзіндік аты бар. Көпмүшеліктің екі шеткі мүшелерінен бастап әрбір мүшесінің коэффициенттері тең теңдеулер симметриялы (қайталамалы) теңдеулер делінеді. Симметриялы теңдеулерді шешудің өзіндік тәсілі бар. Теңдеуді шешу үшін теңдеудің екі жағын да 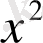-қа бөлеміз:
,
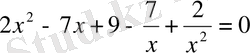Бірінші мен соңғы, екінші мен төртінші мүшелерді топтап ортақ көбейткішті жақша сыртына шығарсақ

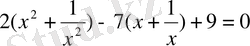
болады.
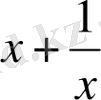=y жаңа белгілеу енгізейік. Бұл теңдіктің екі жағын квадраттасақ:
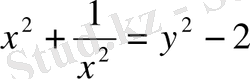болады.
Енді теңдеуді мына түрде жазуға болады:
, яғни .
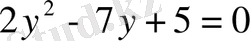Соңғы теңдеудің шешімдері
Осыдан 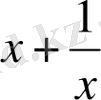=1; 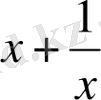= теңдеулер жиынтығы шешіледі.
Жауабы: 2; .
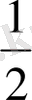5. Теңдеулерді шешудің функционалды-грфиктік әдісі
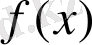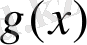= теңдеуін функционалды-графиктік әдісіпен шешу үшін:
1) y= және у = функцияларының графиктері салынады;
2) графиктер қиылысса, қиылысу нүктесін табады.
Графиктердің қиылысу нүктесінің абссицасы теңдеудің түбірі болады.
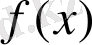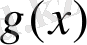y= және у = функцияларының графиктері қиылыспаса теңдеудің шешімі жоқ.
Бұл әдіс теңдеудің түбірлерінің санын және теңдеудің түбірлерін дәл немесе жуықтап анықтауға мүмкіндік береді.
Егер Х аралығында y= 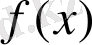және у = 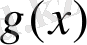функцияларының бірі өсетін, ал екіншісі кемитін болса, онда 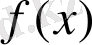= 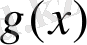теңдеуінің осы аралықта жалғыз түбірі болады (1,a-сурет) немесе ешбір түбірі болмайды (1,ә-сурет).
өседі
кемиді
x
y
O
ә)
O
y
x
өседі
кемиді
жалғыз түбірі
а)

1-сурет

1-мысал. 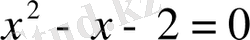теңдеуін шешу.
Ш е ш у і. Берілген теңдеуді = x +2 түрінде жазып аламыз.
1. y = және y = x +2 саламыз;
2. Бұл графиктердің қиылысу нүктелер (-1;1), (2;4) (2-cурет).
O
x
y
-1
1

2- сурет
Жауабы: 1;2.
2-мысал. 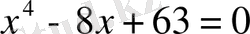теңдеуін шешу керек.
Ш е ш у і. Теңдеуді шешу үшін теңдіктің сол жағын көбейткіштерге жіктеу керек. Бұл оңайға түспейді. Бірақ жіктеуге болады.
Егер теңдеуді = 8x - 63 түрінде жазып, у = және у= 8x - 63 функцияларының графигін ең болмағанда схемалық түрде салатын болсақ, олардың қиылыспайтындығына көзіміз жетеді (3 - сурет)

x
O
y

-63

3-сурет

Егер Х аралығында y= 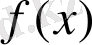және у =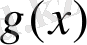функцияларының бірі өсетін, екіншісі кемитін болса және қандайда бір жолмен 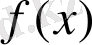= 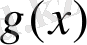теңдеуінің бір түбірін анықтай алсақ, онда теңдеу толық шешілген, ол түбір теңдеудің жалғыз түбірі.
3-мысал. Теңдеуді шешу керек:

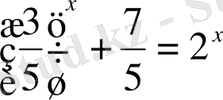
Ш е ш у і. x= 1 теңдеудің бір түбірі болатындығын тағайындау қиын емес.
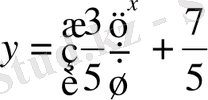функциясы кемімелі, ал 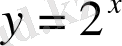функциясы өспелі, олай болса теңдеудің x= 1-ден басқа түбірлері жоқ.
Жауабы: 1.
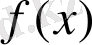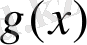Егер y= функциясы Х аралығындағы ең үлкен мәні А және және у = функциясының ең кіші мәні де сол А-ға тең болса, онда Х аралығында 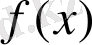= 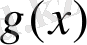теңдеуі

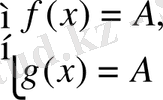
теңдеулер жүйесімен мәндес.
4-мысал. Теңдеуді шеш
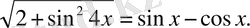
Ш е ш у і:f(x) = болсын, онда f(x) 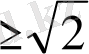болады. Ал g(x)=sinx +cosx болса, онда
g(x) = =
=
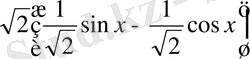Бұдан g(x)екені белгілі.
Сонымен 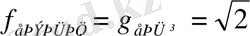болғандықтан = теңдеуін шешу мынадай теңдеулер жүйесін шешуге алып келеді

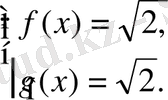
яғни мынадай теңдеулер жүйесін шешеміз:

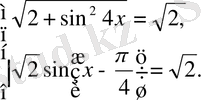
Теңдеулер жүйесінің бірінші теңдеуін шешеміз: sin4x=0, 4x=, x=.
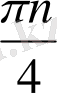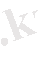
Жүйенің екінші теңдеуін шешеміз:

түбірлер үйірі, х = 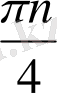түбірлер үйірінің құрамына енеді, сондықтан берілген теңдеудің түбірлері.
Жауабы: .

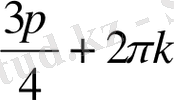3.3. Мәндес теңдеулер

Теңдеулерді шешу кезінде әр түрлі түрлендірулер жүргізіп, алдыңғымен салыстырғанда қарапайым түрге келтіреді. Түрлендірулер тізбегі нәтижесінде пайда болған, соңғы теңдеудің шешімдері берілген теңдеудің түбірлері бола ма, бөгде түбірлер қайдан пайда болды немесе теңдеудің түбірлерінің жоғалып кету жағдайлыры неліктен орын алды деген мәселелер мәндес теңдеулер ұғымымен байланысты. Қандай теңдеулер мәндес деп аталынады, қандай түрлендірулер мәндес түрлендіру болады, қандай жағдайда мәндес емес, оны қалай білуге болады, т. б. мәселелерді оқушылар саналы түрде меңгеруі керек.
Мектеп математика курсында мәндес түрлендіру ұғымы біртіндеп, оқушыларда ол ұғымға деген қажеттілік пайда болып, белгілі бір тәжірибе жинақталғанда енгізіледі. Математика тілінде қандай да бір жаңа терминнің пайда болуы, оған деген қажеттілік болғанда ғана енгізілетінін оқушы түсіну тиіс.
Сызықтық теңдеулер мен квадрат теңдеулерді оқып үйрену кезінде мәндес теңдеу және мәндес түрлендіру туралы мәселе көтерілмейді. Себебі бұл жерде мәндес емес түрлендіру мүлде болмайды, сондықтан мәндес теңдеу терминін енгізуге деген қажеттілік те жоқ.
Алгебралық бөлшектерді оқып үйренуге байланысты, бөлшек рационал теңдеулердің бөлімінен құтылу кезінде бөгде түбірлердің пайда болуы туралы алғашқы түсінік беріледі. Сол кезде бірінші рет мәндес теңдеу термині енгізіледі. Осы кезде мәндес теңдеу ұғымын енгізуге деген қажеттілік те пайда болады, тәжірибе де жинақталады.
Түбiрлерi бiрдей болатын екi теңдеудi өзара мәндес теңдеулер деп атайды. Бір теңдеудің әрбір түбірі екінші теңдеуді де қанағаттандырса және керісінше, екінші теңдеудің кез келген түбірі бірінші теңдеуді қанағаттандырса, онда олар мәндес немесе эквивалент теңдеулер делінеді. Дербес жағдайда, түбiрлерi жоқ барлық теңдеулер өзара мәндес. Мысалы, мына теңдеулер мәндес:
1. х - 2=0 және 2[х]=4,
2. sinx=2 және =-1.
Егер = теңдеуінің әрбір түбірі бір уақытта = теңдеуінің де түбірлері болса, онда = теңдеуі = теңдеуінің салдары деп, немесе салдар-теңдеу деп аталады.
= теңдеуі =теңдеуінің салдары екендігін көрсету үшін, =теңдеуін қанағаттандыратын х-тің барлық мәндері =теңдеуін қанағаттандыратындығына көз жеткізу жеткілікті.
х2-8х=0 теңдеуінің салдары (х2-8х)(х+5)=0 теңдеуі болатындығын көрсету үшін х2-8х=0 теңдеуінің әрбір түбірі (х2-8х)(х+5)=0 теңдеуінің де шешімі болатындығына көз жеткізіледі.
Егер екі теңдеудің бірі екіншісінің салдары және керісінше болса, онда екі теңдеу мәндес болады.
Қандай жағдайда бір теңдеуден екінші теңдеуге өткенде мәндес түрлендіру болады деген мәселеге тоқталайық.
Төмендегідей үш теорема орындалатындай түрлендіру жасағанда бір теңдеуден екінші теңдеуге өту әр уақытта мәндес түрлендіру болады.
1-теорема. Егер теңдеудің қандай да бір мүшесін кері таңбамен теңдіктің бір жағынан екінші жағына шығарса, онда пайда болған теңдеу берілген теңдеумен мәндес болады.
2-теорема. Егер теңдеудің екі жағын да бірдей тақ көрсеткішті дәрежеге шығарсақ, онда пайда болған теңдеу берілген теңдеумен мәндес болады.
3-теорема. 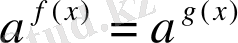(мұндағы а 0, a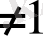)теңдеуі f(x) = g(x) теңдеуімен мәндес.
Бұл теоремаларды қолданғанда бөгде түбір пайда болмайды, түбірлердің жоғалып кетуі де мүмкін емес.
Ал мына төмендегі теоремалар белгілі бір шарттар орындалғанда ғана жұмыс істейді, яғни оларды қолдану кезінде ұқыптылықты қажет етеді.
4-теорема. Егер f(x) = g(x) теңдеуінің екі жағын да бірдей, берілген теңдеудің анықталу облысының барлық жерінде мағынасы бар, осы облыстың ешбір жерінде нөлге айналмайтын h(х) өрнегіне көбейтсе, онда берілген теңдеуге мәндес f(x)h(х) = g(x)h(х) теңдеуі пайда болады.
Бұл теоремамен жұмыс істегенде теңдіктің екі жағына да көбейтілетін h(х) өрнегінің:
1) берілген теңдеудің анықталу облысында мағынасы болуы;
2) берілген теңдеудің анықталу облысында нөлге айналмайтын болуы ескерілуі керек.
4-теоремадан ешқандай шартты талап етпейтін төмендегі салдар шығады: егер теңдіктің екі жағын да нөлден өзгеше с санына көбейтсе немесе бөлсе берілген теңдеуге мәндес теңдеу шығады.
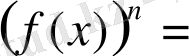
5-теорема. Егер f(x)=g(x) теңдеуінің анықталу облысында теңдіктің екі жағы да теріс емес болса, онда теңдіктің екі жағын да бірдей жұп дәрежеге шығарғаннан кейін пайда болған теңдеуі берілген теңдеуге мәндес.
f(x) = g(x) теңдеуінің екі жағын да жұп дәрежеге шығару үшін, теңдеудің анықталу облысында f(x)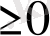, g(x) шарттар орындалуы қажет.
6-теорема. және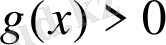болса, онда 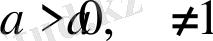болғанда 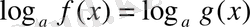теңдеуі f(x) = g(x) теңдеуімен мәндес.
Бұл теорема бойынша 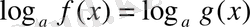(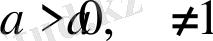) теңдеуінен f(x) = g(x) теңдеуіне өту үшін 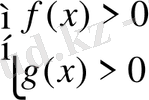теңсіздіктер жүйесін қанағаттандыру керек.
Егер теңдеуді шешу үдерісінде 4,5,6-теоремаларының шартындағы шектеулердің бірінің орындалуын тексерместен, қорытындысын ғана пайдалансақ салдар-теорема аламыз. Оған негізгі себеп, берілген теңдеудің анықталу облысының кеңейіп кетуінде.
Егер теңдеуді шешудің белгілі бір кезеңінде теңдеудің екі жағын да қандайда бір өрнекке көбейтсек (әрине ол өрнек теңдеудің анықталу облысында мағынасы бар болуы керек), немесе теңдіктің екі жағын да жұп дәрежеге шығарсақ, немесе логарифмдік теңдеулерді шығару барысында теңдіктің екі жағындағы бірдей негіздегі логарифм таңбасын тастап кетіп жазатын болсақ, онда табылған барлық түбірлерді міндетті тексеру керек.
Басқаша: теңдеуді түрлендіру үдерісінің белгілі бір кезеңінде теңдеудің анықталу облысының кеңеюі орын алса, онда міндетті түрде барлық табылған түбірлерді тексеруге тура келеді.
Енді мектеп математика курсы деңгейінде қандай түрлендірулер жасаған кезде теңдеудің анықталу облысының кеңейіп кетуі мүмкін деген орынды сұрақ туады.
Теңдеудің анықталу облысының кеңейіп кету жағдайлары үшеу:
1. Бөлшектің бөлімінен құтқару кезінде. Теңдеудің құрамындағы бөлшектің бөлімінде g(x) өрнегі болса, теңдеудің екі жағын да g(x)0 өрнегіне көбейтіп немесе бөлшекті қысқарту арқылы бөлшек бөлімсіз жазылады. Мұны еркін сөйлеу кезінде бөлшекті бөлімінен құтқару деп айта береді. Теңдеуде бөлім болмағаннан кейін шектеу де жоқ деген сөз. Демек теңдеудің анықталу облысы кеңейді.
2. Логарифмді тастап кету кезінде. Бірдей негіздегі логарифмдердің теңдігінен логарифм таңбасының астындағы өрнектердің теңдігіне көшу теңдеудің анықталу облысын кеңейтеді. Себебі логарифм таңбасы астындағы өрнектердің оң болатындығы ескерілмей отыр.
3. n жұп болғандағы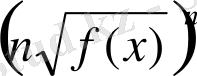= f(x) формуласын пайдалану кезінде. Шындығында да, егер мысалы, 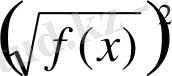өрнегінің анықталу облысы f(x) 0 теңсіздігімен беріледі. Егер 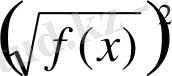өрнегін f(x) өрнегімен алмастырылса, f(x) еркін қарастырылады да f(x) 0 шектелуі алынып тасталады, яғни анықталу облыс кеңейеді.
Теңдеудің түбілерін тексеру екі жолмен жүргізіледі:
1) барлық түбірлерді берілген теңдеуге қойып тексергенде, теңдеуді қанағаттандыратындар (дұрыс санды теңдікке айналдыратындар) теңдеудің түбірлері, ал қанағаттандырмайтындары бөгде түбірлер болады.
2) табылған түбірлердің берілген теңдеудің анықталу облысына тиістілігі тексеріледі. Түбір анықталу облысында жататын болса, ол берілген теңдеудің түбірі, ал жатпаса бөгде түбір болғаны.
Теңдеудің түбірлерін анықталу облысы бойынша тексеру тәсілі бір теңдеуден екінші теңдеуге өту кезіндегі анықталу облысының кеңейіп кетуінен басқа мәндес емес түрлендірулер болмаған жағдайда ғана тиімді. Бұл логарифмдік теңдеулерді шешу кезінде орынды.
Ал, иррационал теңдеулерді шешу кезінде мәселе күрделілеу: теңдеудің табылған түбірлері анықталу облысына тиісті болғанымен де, олардың ішінде бөгде түбірлер болуы мүмкін. Мұндай жағдай теңдіктің екі жағын жұп дәрежеге шығаруға байланысты болады.
Енді теңдеудің түбірлері жоғалып кететін жағдайларға тоқталайық.
Мектеп математика курсы деңгейінде теңдеудің түбірінің жоғалып кетуі негізінен екі себепке байланысты:
1) теңдіктің екі жағын да бірдей h(x) өрнегіне бөлу кезінде (h(x) 0 екендігі анық белгілі болған жағдайдан басқа);
2) бір теңдеуден екінші теңдеуге өту кезінде теңдеудің анықталу облысының таралып кетуі.
Бірінші жағдайдағы кемшіліктерімен күресу қиын емес: өрнектің нөлге тең емес екендігі алдын ала белгілі болмаса, теңдеудің екі жағында бірдей ол өрнекке бөліп жіберуге тыйым салынады.
Оқушыны
теңдеуін
,

деп шешуге үйрету керек.
Екінші жағдай күрделі. Мұнда теңдеуді шешу үдерісінде формулаларды дұрыс қолданбауға байланысты түбірлердің жоғалып кетуі орын алады:
1. деп жазудың орнына деп қате жібереді.
2. деп жазудың орнына деп жазады.
3. деп жазудың орнынадеп қателеседі.
Тригонометриялық теңдеулерді шешуде түбірлердің жоғалып кетуіне алып келетін тригонометриялық формулаларды келтіріп кетейік.
1. ctgx =. Теңдіктің сол жағының анықталу облысы ; оң жағының анықталу облысы екі шарттың орындалуына байланысты: tgx 0, яғни ; cos 0; яғни . сtgx-ты -пен алмастырғанда анықталу облыс тарылады: шектелуінен басқа, қосымша шектелуі пайда болды, осының салдарынан түбірлердің жоғалып кетуі мүмкін.
ctgx = формуласын пайдаланғанда x = мәнін бастапқы теңдеуге қойып тексеру керек. Теңдеуді қанағаттандырса, ол теңдеудің түбірі болғаны.
2. tg2x = . Теңдіктің сол жағының анықталу облысы cos2x 0, яғни 2x немесе x; теңдіктің оң жағының анықталу облысы екі шарттың орындалуы арқылы табылады: яғни x, және cosx 0, яғни . Теңдіктің cол жағын оң жағымен алмастырғанда деген қосымша шектеу пайда болды. x = тексеру керек.
3. Бұл жерде теңдіктің сол жағын оң жағымен алмастырғанда шектеу пайда болады.
4. tg = tg үшін , яғни x ; ал үшін: x . Анықталу обылыс тарылды: x шектелуіне қосымша x шектелуі пайда болды.
Ал осы формулаға ұқсас tg формуласын пайдаланғаннан анықталу облысында тарылу болмайды. Теңдіктің сол жағы мен оң жағының анықталу облыстары бірдей: x .
5. Мұндай алмастырулар арқылы шешілетін теңдеудің x = түбірінің жоғалып кетуі мүмкін. Бұл мәнді бастапқы теңдеуге қойып тексеру керек.
Түбірдің жоғалып кетуі х-тің кез келген мәнінде анықталған sinx пен cosx өрнегін, анықталу облысының тарылуына алып келетін tg өрнегімен алмастырылуына байланысты болады.
Мысал. sinx - cosx =1 теңдеуін шешу керек.
Ш е ш у і. Теңдеуді шешу үшін формуласын пайдаланып, tg= u алмастыруын жасаймыз. tg-тің анықталу облысы , яғни x .
Берілген теңдеу мына түрге келеді , бұдан u=1, яғни tg=1,
Бірақ, берілген теңдеуді х = мәндері де қанағаттандырады. Теңдеу түбірлерінің бұл мәндерінің жоғалып кетуі х-тің кез келген мәнінде анықталған sinx пен cosx өрнегін, олардың анықталу облысын тарылтатын tg өрнегімен алмастыруымызға байланысты келіп шықты.
Жауабы: , х = .
1.Сызықтық теңдеуді шешу тақырыбын жүйелі оқыту.
Сызықтық теңдеуді шешу бастауыш сынып математикасын
оқытудан басталады.
1. Бастауыш сыныптарда мынадай сызықтық теңдеудi шешу қарастырылады: 7+х=10, x-3=10+5, x(17-10)=70, x:2+10=30 т.с.с. Белгiсiз санды алдымен iрiктеп, таңдап алу әдiсiн пайдаланып теңдеудуің түбірі табылады. Кейiн, теңдеудің түбірін табу арифметикалық амалдардың компоненттерi мен нәтижелерiнiң арасындағы байланысқа сүйенiп табуға үйретіледі. Мысалы, бiрiншi теңдеудi шешкенде оқушылар былайша пайымдайды: Белгiсiз қосылғышты анықтау үшiн қосындыдан белгiлi қосылғышты алуымыз қажет: х=10-7, х=3.
Теңдеулермен танысу формальдi түрде жүргiзiлмейдi. Мысалы, мынадай есеп қарастырылады: Белгiсiз санға 3-тi қосқанда 8 шыққан. Белгiсiз санды анықтаңдар. Есеп қысқаша түрде былайша жазылады: ? + 3=8. ? символының орнына қойылатын сан таңдап алу әдiсiмен анықталады. Бұдан кейiн белгiсiз санды x арқылы белгiлеп оны былайша жазуға болатындағы айтылады: х+3=8.
Бастауыш сыныптарда теңсiздiктер де таңдап алу әдiсiмен шығарылады, көбiнесе теңсiздiк шешiмдерiнiң шектi бөлiктерi ғана табылады.
2. 5-сыныпта да тендеулер арифметикалық амалдардың компоненттерi мен нәтижелерiнiң арасындағы байланыс бойынша шешiледi, көбiнесе алдын-ала өрнектердi ықшамдап алады. Мысалы‚ 13899+х = 2716+13899. Оқушылар көбейтудiң қосу (азайту) амалына қатысты үлестiрiмдiлiк заңын пайдаланып‚ мынадай 4х+4х=424; 15а - 8а = 714 т.с.с. теңдеулердi шешедi. Ондық бөлшектердi өту кезiнде мынадай теңдеулер шешiледi:
8,6-(x+2,75)=1,85; x+2,8=3,72+0,38; 45,7x+0,3x-2,4=89,6.
Бұл теңдеудердi шешу де арифметикалық амалдардың нәтижесi мен компоненттерiнiң қасиеттерiне негiзделген.
3. 6-сыныпта оң таңбалы және терiс таңбалы сандарды өткенде сызықтық теңдеудiң ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.