GeoGebra арқылы жазықтықтағы геометриялық салу есептерін шешу


12-Лекция
Лекция тақырыбы: Geogebra пакетін қолданып жазықтықтағы салу есептерін шешу
Жоспар:
- Жазықтықтағы салу есептері
- Теңбүйірлі үшбұрышты салу есебі
- Кесіндіге орта перпендикуляр жүргізу
- Берілген түзуге параллель түзу салу
- Үшбұрышқа сырттай шеңбер салу
- Берілген фигураға ұқсас фигура салу
- Берілген фигураға симметриялы фигура салу
- Жазықтықтағы салу есептері
Геометриялық салу есебі дегеніміз алдын ала берілген құралдарды пайдалану арқылы есепте көрсетілген талаптарды ескере отырып фигура салу.
Есеп шартын қанағаттандыратын әрбір салынған фигура сол салу есебінің шешімі делінеді. Кейде салу есебінің шартын қанағаттандыратын бірнеше фигура болуы мүмкін (Мысалы, екі қабырғасы бойынша түрлі үшбұрыш салуға болады) . Салу есебі шешілді делінеді, егер оның барлық шешімдері табылса.
Есеп шартын қанағаттандыратын фигуралар бір-бірінен формасы мен өлшемдері арқылы немесе тек жазықтықтағы орны арқылы ғана өзгешеленуі мүмкін. Соңғы жағдайда есептің бір ғана шешімі бар делінеді. Сондықтан, көп жағдайда, есептің өзара тең емес шешімдері ізделінеді. Шешімі шексіз көп болатын салу есептері де болады. Мысалы, бір түзуге жанасатын шеңбер салу, есебін қанағаттандыратын шексіз көп фигуралар болады. Мұндай есептерді анықталмаған салу есептері дейді. Ондай есептер есеп шарты жеткіліксіз берілген жағдайлардан туындайды және олар шешілді делінеді, егер ол есепті шешудің жалпы жолы табылса.
Мысалы, А және В екі нүктесін басып өтетін шеңбердің центрі АВ кесіндісінің қақ ортасынан жүргізілген оған перпендикуляр түзудің кез-келген нүктесі болады, ал радиусы сол нүкте мен А нүктесінің (немесе В нүктесі) арасы болады.
Кейде есеп шартын қанағаттандыратын фигураның мүлдем болмауы мүмкін, болған күннің өзінде берілген құралдармен салынбауы мүмкін. Мысалы, концентрлі шеңберлерге ортақ жанама мүлдем болмайды. Мұндай жағдайда, есеп шартын қанағаттандыратын фигураның жоқтығын дәлелдей алсақ есеп шешілді делінеді.
Кейде есепке шарт артық қойылуы себебінен есептің шешімі болмауы мүмкін. Мысалы 4 нүктені басып өтетін шеңбер салу, екі қабырғасы мен екі бұрышы берілген үшбұрыш салу есептерінде шарт артық қойылған. Мұндай есептерді артығымен шарт қойылған есептер дейді.
Жалпы n-бұрышты фигураны бір мәнді салу үшін 2n-3 шарт берілуі керек. Сонда үшбұрышты салу үшін 2n-3=2·3-3=3 шарт, төртбұрышты салу үшін 2n-3=2·4-3= 5 шарт берілуі тиіс. Салу есебін орындағанда есептің барлық мүмкін жағдайларын қарастыру керек. Мысалы, шеңберге А нүктеден жанама жүргіз десе, онда А нүктесінің шеңбер бойында, шеңбермен шектелген дөңгелектің ішінде немесе одан тыс жататын жағдайларын жеке-жеке қарастыру керек.
Салу аксиомалары немесе постулаттары делінетін тұжырымдар:
П-1. Салынған екі нүктеден өтетін түзуді салу.
П-2. Салынған нүктені центр етіп, салынған екі нүкте арасын радиус етіп шеңбер салу.
П-3. Параллель емес екі түзудің қиылысу нүктесін салу.
П-4. Салынған шеңбер мен салынған түзудің қиылысу нүктесін салу, егер олар қиылысатын болса.
П-5. Салынған екі шеңбердің қиылысу нүктесін салу, егер олар қиылысатын болса.
Салу есебін жалпы түрде былайша тұжырымдауға болады: саны шектеулі салынған негізгі фигуралар F 1 , F 2 , . . , F n берілген және ізделіп отырған салынбаған F фигураның қасиетінің сипаттамалары берілген. Жоғарыда келтірілген П-1, 2, 3, 4, 5 постулаттарды пайдалана отырып, F фигураны анықтайтын салынған негізгі фигуралардың шекті жиынын табу керек.
Салу есептерін шешудің жалпы схемасы
Салу есебін шешу - сол салу есебін шешудің жолын анықтау, анықталған жол бойынша оны салу және ол есептің шешімі қандай жағдайларда болады, болса қанша болады, қандай жағдайда есептің шешімі болмайды деген сұрақтарға жауап іздеуден тұрады.
Қарапайым деген салу есебін шешудің өзі бірнеше қадамнан тұрады. Сондықтан салу есебін шешуде белгілі бір схеманы басшылыққа алған жөн. Қалыптасқан схема бойынша салу есебін шешу 4 кезеңнен: Талдау, салу, дәлелдеу, зерттеуден тұрады. Әрине салу есебін шешуде бұл схеманы барлық кезде қатаң қолдану міндетті емес, кейде бұдан өзге жолдарды пайдаланған тиімді болады. Дегенмен бұл схема геометриялық салу есебін шешуді жеңілдетеді.
Бұл схеманың мәні төмендегідей
1. Талдау кезеңі. Бұл кезеңде есеп шартында берілген фигуралар мен салынатын фигура арасындағы қатыстарды анықтайды. Ол үшін есеп шешілген деп ұйғарып, салынатын фигураның жобасы кескінделеді. Осы жоба кескінде берілген фигуралар мен салынатын фигуралар арасындағы қатыстарды талдай отырып, ізделінді фигураны салу қадамдарын белгілейді. Сөйтіп, талдау кезеңі есепті шешу, фигураны салу жолдарын іздестіру нәтижесінде ізделінді фигураны салу қадамдарын тізбектей белгілеумен аяқталады.
2. Салу кезеңі. Бұл кезеңде талдау кезеңінде анықталған салу қадамдарын циркуль және сызғыш арқылы бірінен соң бірін тізбектей орындайды. Сонда талдау кезеңінде салынған кескін жобасы іздеген фигураның нағыз кескініне айналады.
3. Дәлелдеу кезеңі. Бұл кезеңде салынған фигура есептің барлық шарттарын қанағаттандыратынын дәлелдейді. Сөйтіп салынған фигураның, шынындығында, іздеп отырған фигура екеніне көз жеткізіледі.
4. Зерттеу кезеңі. Бұл кезеңде мына сұрақтарға жауап беріледі:
а) Таңдап алған әдіспен есепті шешу әруақытта мүмкін бе, яғни циркуль және сызғышты пайдаланып оны салуға болады ма?
б) Есептің қандай жағдайда шешімі бар және қанша, қандай жағдайда шешімі болмайды?
Міне осы сұрақтарға жауап іздеу зерттеу кезеңінің міндеті болып табылады. Яғни, зерттеу бөлімінің міндеті есептің шешілу шарттарын және шешім санын анықтау. Бұл кезеңде есептің барлық мүмкін жағдайларын қарастыру үшін әрбір салу қадамдарын зерттеген жөн.
Циркуль және сызғыш арқылы салынатын негізгі салу есептерінің қатарына мына есептерді жатқызуға болады:
- Берілген сәулеге оның төбесінен бастап берілген кесіндіні өлшеп салу;
- Берілген сәуледен берілген жарты жазықтықта берілген бұрышты өлшеп салу;
- Бұрыштың биссектрисасын жүргізу;
- Берілген кесіндінің орта перпендикулярын жүргізу;
- Кесіндінің ортасын салу;
- Үш қабырғасы бойынша үшбұрыш салу;
- Екі қабырғасы мен арасындағы бұрышы бойынша үшбұрыш салу;
- Бір қабырғасы мен оған іргелес екі бұрышы бойынша үшбұрыш салу;
- Берілген түзуге берілген нүктеден перпендикуляр түзу жүргізу;
- Берілген нүктеден берілген түзуге параллель түзу жүргізу;
- Гипотенузасы мен бір сүйір бұрышы бойынша тікбұрышты үшбұрыш салу;
- Гипотенузасы мен бір катеті бойынша тікбұрышты үшбұрыш салу;
- Шеңберге оның берілген нүктесінен жанама жүргізу т. с. с.
- Теңбүйірлі үшбұрышты салу есебі
7 сыныпта өтілетін Үшбұрыштың түрлері тақырыбы бойынша теңбүйірлі үшбұрышты салу.
Кесте 4 - командалар тізбесінің сипатталуы.







Жоғарыда көрсетілген іс-әрекеттерді орындау арқылы «Geogebra» алаңында төмендегідей кескінді аламыз.
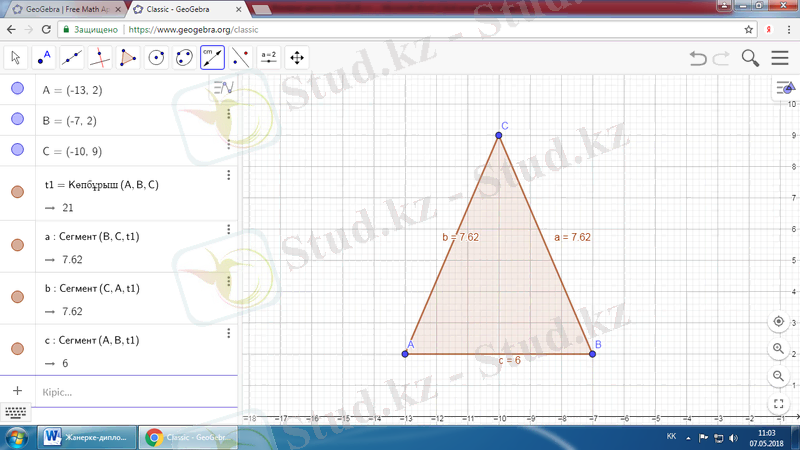
а
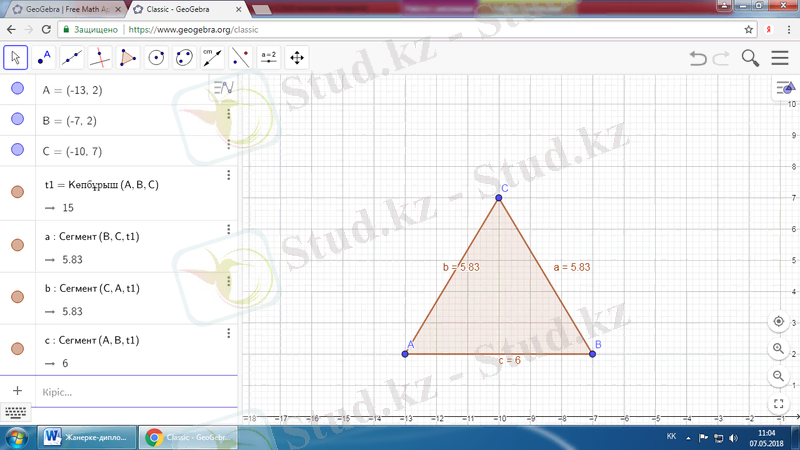
в
Салынған теңбүйірлі үшбұрышты Жылжыту құралымен С нүктесін жылжытып көреміз, сонда үшбұрыштың бүйір қабырғаларының өлшемдері бір-біріне тең болатынын байқаймыз.
- Кесіндіге орта перпендикуляр жүргізу
2-мысал. «Geogebra» бағдарламасының көмегімен кесіндіге орта перпендикуляр жүргізу.
Кесте 5 - командалар тізбесінің сипатталуы





Жоғарыда көрсетілген іс-әрекеттерді орындау арқылы «Geogebra» алаңында төмендегідей кескінді аламыз.
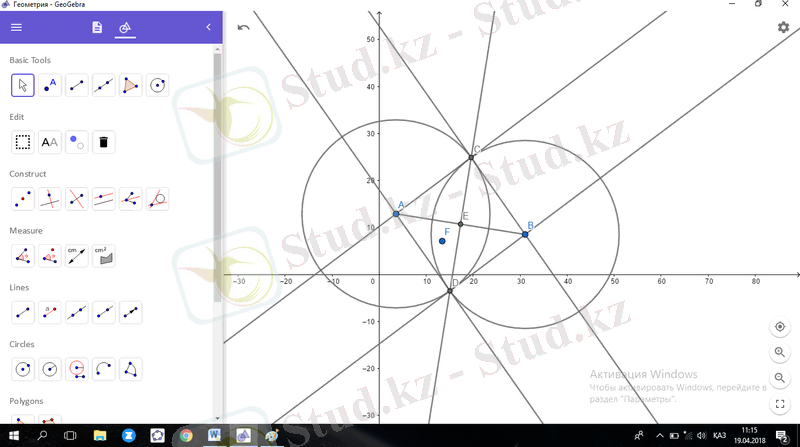
Сурет 27 - Кесіндіге орта перпендикуляр жүргізу.
Сонымен, «Geogebra» бағдарламасындағы Екі нүкте арасындағы кесінді құралын пайдаланып Кесіндіге орта перпендикуляр жүргіздік.
4. Берілген түзуге параллель түзу салу
«Geogebra» бағдарламасының көмегімен берілген түзуге параллель түзу сызу.
Кесте 6 - командалар тізбесінің сипатталуы.











Оны дәлелдеу үшін G және F, E және C нүктелерін қосамыз.
EC=GC, FE=FG, өйткені олар шеңбердің радиустары болып табылады. Демек, шыққан фигура ромб болып табылады. Ал ромбтың қабырғалары бір-біріне параллель болады.
Осындай іс-әрекеттерді орындау арқылы экранда берілген түзуге параллель түзулер саламыз (сурет 28) .
«Geogebra» бағдарламасындағы Екі нүкте арқылы түзу жүргізу құралын қолдана отырып, параллель түзу салу ережесі бойынша геометриялық жазықтықта берілген түзуге параллель түзу салу мүмкіндігін қарастырдық. Алынған кескінді жылжыту арқылы түзулердің параллелдігі бұзылмайтынын байқауға болады.
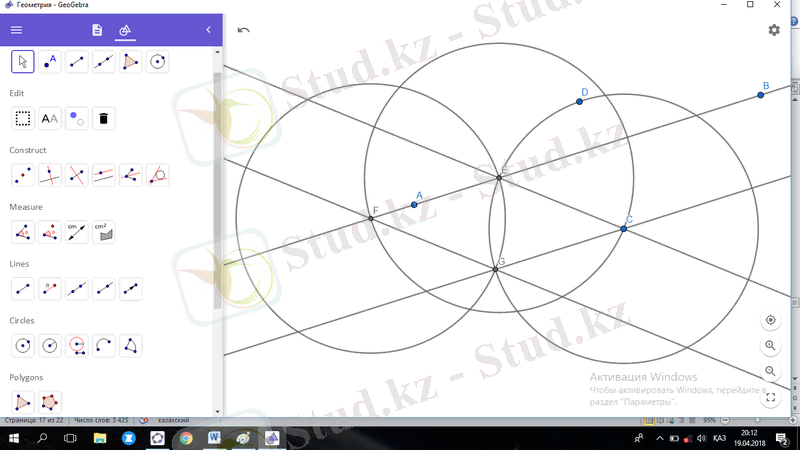
Сурет 28 - Берілген түзуге параллель түзу сызу.
5. Берілген бұрышқа тең бұрыш салу
«Geogebra» бағдарламасының көмегімен берілген бұрышқа тең бұрыш салу.
Кесте 7 - командалар тізбесінің сипатталуы.












«Geogebra» бағдарламасындағы Нүкте және центр арқылы шеңбер салу құралын пайдаланып берілген бұрышқа тең бұрыш салдық.
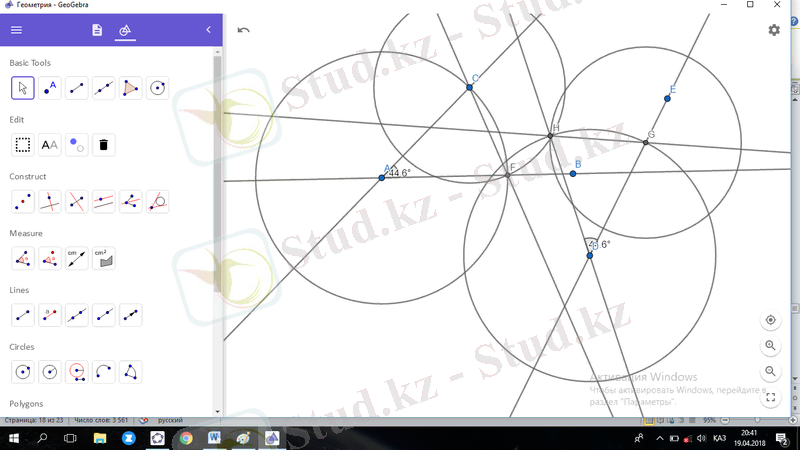
Сурет 29- Берілген бұрышқа тең бұрыш салу.
- Үшбұрышқа сырттай шеңбер салу
ГеоГебраны пайдаланып, АВС үшбұрышына сырттай шеңбер салу есебін қарастырайық.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz