GeoGebra-да параметрлік планиметриялық есептерді шешу әдістері


13-Лекция
Лекция тақырыбы: Geogebra-да планиметриялық есептерді шешу жолдары
Жоспар:
- Параметрлері өзгермелі болатын жағдайда геометриялық фигураларды кескіндеу
- Geogebra-да планиметрия есептерін шешу мысалдары
1. Параметрлері өзгермелі болатын жағдайда геометриялық фигураларды кескіндеу
Параметрлері бар геометриялық есептердің белгілері:
- есептің шартында әріппен берілген немесе белгісіз геометриялық шамалардың бар болуы;
- есеп талаптарына мүмкін болатын шешідерінің санын анықтау, шарттарды айқындау, тәуелділік сипатын анықтау сұрақтарын енгізу.
Компьютерлік шешімі аналитикалық шешімнен тәуелсіз алынуы мүмкін есептер параметрлерлі есептерді шешуді оқытудың бірінші кезеңдерінде қолданылуы мүмкін, өйткені олар есепті шешу нәтижесінің параметр мәнінен (немесе параметрлер мәндерінің арақатынасынан) тәуелділігін көрнекі етеді және де "параметр", "параметрдің бақылау мәні", "параметрлі есепті шешу нәтижесі" ұғымдарының мәнін ашуға мүмкіндік береді.
Мысал 1. СD және С 1 D кесінділері центрі А нүктесінде болатын шеңберге одан тысқары жатқан D нүктесінен жүргізілген жанамардың кесінділері болып табылады. Салынған динамикалық кескінде компьютерлік эксперимент жүргізіңіз. СDС 1 бұрышының қандай мәндерінде АD кесіндісінің ортасы: шеңберде жатады, дөңгелектің сыртында жатады, дөңгелектің ішінде жатады? Эксперимент нәтижесін кестеге енгізіңіз.
Геогебрада есептің динамикалық кескінін саламыз (Сурет 1) . Кескінде көрсетілген D нүктесін жылжыту құралы арқылы жылжыта отырып, АD кесіндісінің ортасын әртүрлі жағдайға келтіреміз (сурет 2) . Нәтижені кестеге толтырамыз.
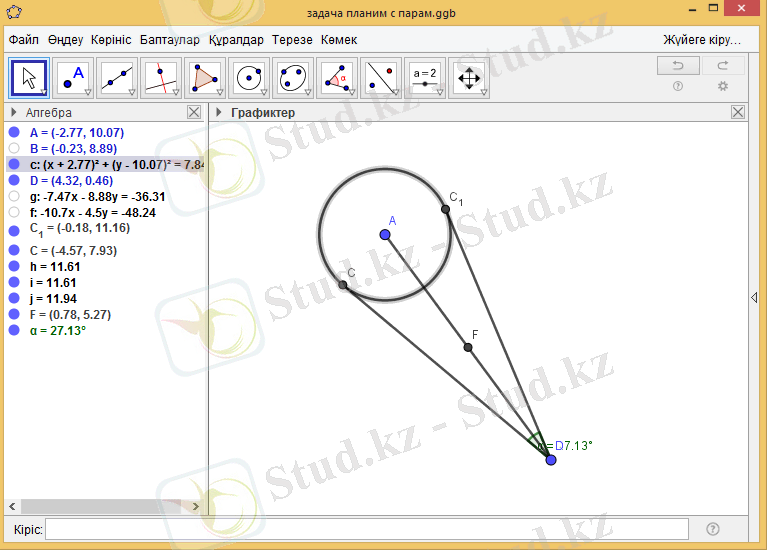
Сурет 1
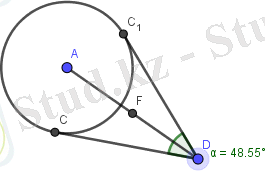 а)
а)
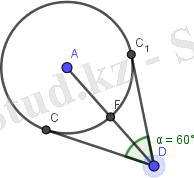 ә)
ә)
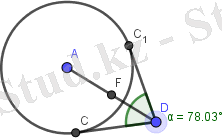 б)
б)
Сурет 2
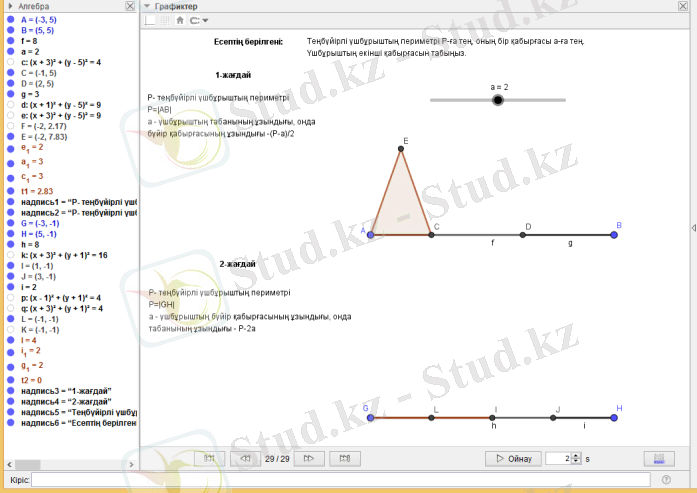
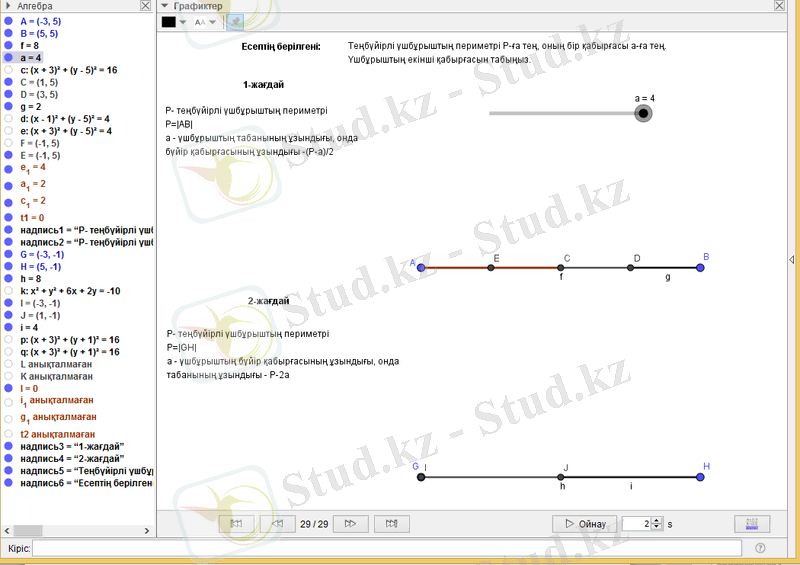
Мысал 2 . Периметрі Р-ға тең, ал бір қабырғасы а-ға тең теңбүйірлі үшбұрыштың екінші қабырғасын табыңыз.
- Есептің неше шешімі бар?
- Есептің шешімінің саны а парамертінің мәніне тәуелді ме?
Есептің аналитикалық шешімі .
1-жағдай. Егерде а -теңбүйірлі үшбұрыштың табанының ұзындығы болса, онда оның бүйір қабырғаларының ұзындығы (Р-а) /2 - ге тең. Осындай қабырғалары бар үшбұрыштың бар болуы үшін төмендегі теңсіздіктер жүйесі орындалуы шарт:
2-жағдай. Егерде а -теңбүйірлі үшбұрыштың бүйір қабырғасының ұзындығы болса, онда оның табанының ұзындығы Р-2а - ға тең. Осындай қабырғалары бар үшбұрыштың бар болуы үшін төмендегі теңсіздіктер жүйесі орындалуы шарт:
Жауабы:
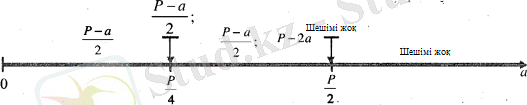
Есептің компьютерлік шешімі . Динамикалық кескінді салу алгоритмі:
- Ұзындығы Р болатын кез келген кесіндіні салу.
- Мәндер облысы 0-ден Р/2-ге дейін өзгеретін а параметрі үшін слайдер салу.
- Егер а- теңбүйірлі үшбұрыштың табанының ұзындығы болса, онда 4-қадамға көшу, әйтпесе 11-қадамға көшу.
- Ұзындығы Р-ға тең кесіндінің бір ұшы центрі болатын, ал радиусы а-ға тең шеңбер салу және оның кесіндімен қиылысу нүктесін белгілеу.
- Кесіндінің қалған бөлігінде оның ортасын белгілеу.
- Бүйір қабырғаның ұзындығын белгілеу үшін анықталған орта нүкте мен Р кесіндісінің екінші ұшын қосатын кесінді салу.
- Үшбұрыш табанының ұштары центр болатын, ал радиусы бүйір қабырғаға тең екі шеңбер салу.
- Салынған шеңберлердің қиылысу нүктелерін белгілеу.
- Төбелері табанның ұштары мен шеңберлердің қиылысу нүктелерінің бірі болатын үшбұрыш салу.
- Үшбұрыш пен периметрді көрсететін кесіндіден басқа барлық объектілерді жасыру.
- а- теңбүйірлі үшбұрыштың бүйір қабырғасының ұзындығы болған жағдайға байланысты екінші суретті салу үшін ұзындығы Р болатын жаңа кесінді салу.
- Ұзындығы Р-ға тең кесіндінің бір ұшы центрі болатын, ал радиусы Р-2а-ға тең (немесе кесіндінің екінші ұшынан радиусы 2а болатын) шеңбер салу және оның кесіндімен қиылысу нүктесін белгілеу.
- 5-10 қадамдарындағы әрекеттерді қайталау (Сурет 3) .

Сурет 3 - Периметрі Р-ға тең, ал бір қабырғасы а-ға тең теңбүйірлі үшбұрыштың динамикалық кескіні.
Динамикалық кескінді пайдаланып, эксперимент жасап көруге болады. Ол үшін слайдерді жылжытып, а параметрін ең төменгі мәннен бастап, жоғары мәнге дейін өзгерте отырып, үшбұрыштың өзгерісін/ бар болуын бақылаймыз.
Қорытынды: Параметрдің бақылау нүктелері мен аралықтары (Сурет 5) :
- а=0 (бұл нүктеде екі үшбұрыш та жойылады) ;
- 0<a<P/4 ( осы аралықта бір үшбұрыш көрінеді) ;
- а=Р/4 (осы нүктеден өткен кезде екінші үшбұрыш пайда болады) ;
- P/4<a<P/2 ( осы аралықта екі үшбұрыш көрінеді) ;
- а=Р/2 (бұл нүктеде екі үшбұрыш та жойылады) .
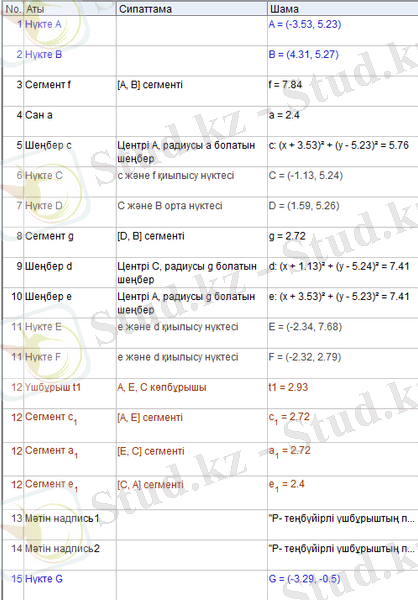
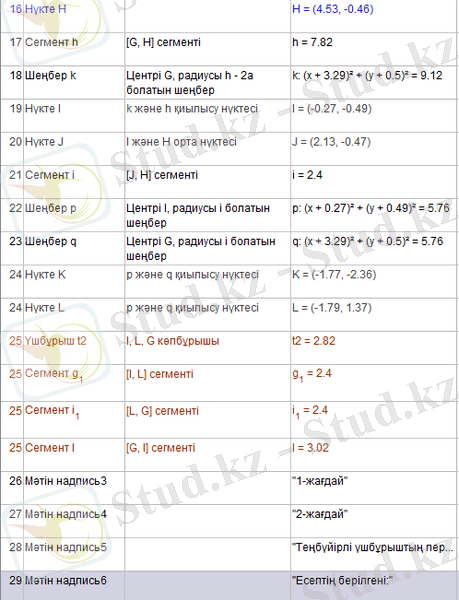
Сурет 4 - Динамикалық кескінді салу әрекеттерінің хаттамасы.
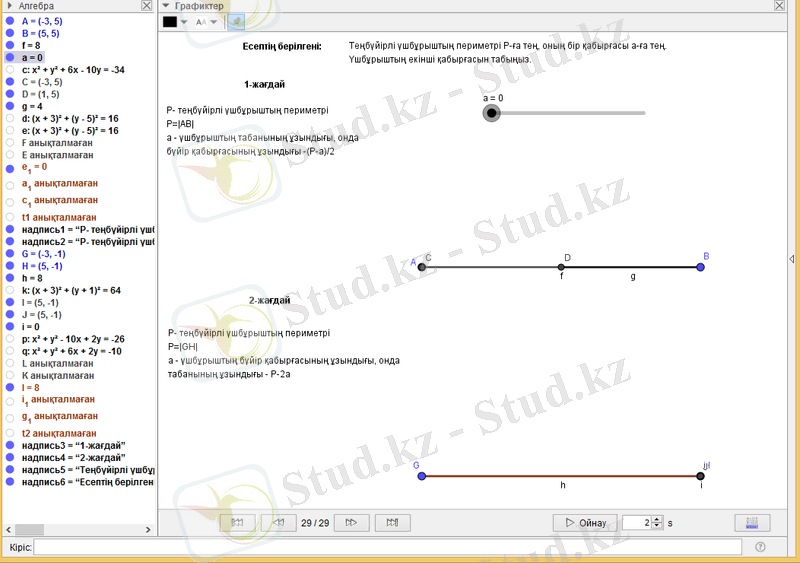

Сурет 5 - Параметрдің бақылау нүктелері мен аралықтарына сәйкес динамикалық кескін көріністері
- Geogebra-да планиметрия есептерін шешу мысалдары
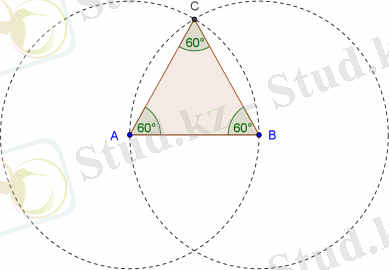
1-мысал . АВ кесіндісі және осы кесіндінің ұштары центрі, ал радиусы осы кесіндінің ұзындығына тең болатын екі шеңбер берілген. Шеңберлердің бір қиылысу нүктесін С деп белгілейік. АВС үшбұрышының барлық бұрыштарын табыңыз. Бұл қандай үшбұрыш?
Шешуі.
2-мысал. АВСD трапециясының табандары АD=16см және ВС=8 см. С төбесі арқылы трапецияны аудандары тең болатын екі көпбұрышқа бөлетін l түзуін жүргізіңіз.
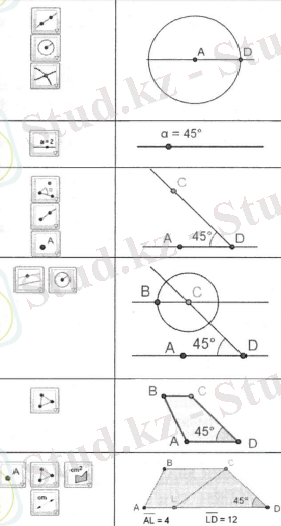
S(АВСL) =32
S(LCD) =32
α=45 0
- Трапецияның табанын саламыз АD=16:
- а түзуін салу
- центрі А нүктесінде, радиусы АD шеңбер салу
- шеңбер мен а түзуінің қиылысуы D нүктесін салу
- Трапецияның бұрышын 00-1800арасында өзгерту үшін α слайдерін құрамыз.
- DА’ сәулесі мен D нүктесі арқылы шамасы берілген α-ға тең болатын бұрышты саламыз.
- DА’ сәулесінде С нүктесін белгілейміз.
- ВС трапециясының табанын саламыз:
- а түзуіне параллель b түзуін салу
- центрі С нүктесінде, радиусы 8-ге тең шеңбер салу
- шеңбер мен b түзуінің қиылысу нүктесі В нүктесін белгілеу
- АВСD трапециясын саламыз.
- АD кесіндісінде L нүктесін белгілейміз.
- АВСL және LCD көпбұрыштарын саламыз.
- Олардың аудандарын есептейміз.
- L нүктесінен А және D нүктелеріне дейінгі қашықтықты өлшейміз.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz