Geogebra көмегімен стереометриялық салу есептерін шешу


15-Лекция
Лекция тақырыбы: Geogebra пакетін қолданып кеңістіктегі салу есептерін шешу
Жоспар:
- Geogebra ортасында кеңістіктік фигураларды салу.
- Кубқа іштей және сырттай сфера салу.
- Кубқа іштей көпбұрыш салу.
- Дұрыс пирамидаға сырттай конус салу.
- Пирамидаға қима салу.
- Кеңістіктік фигураларды анимациялау.
- Стереометрияның есептерін Geogebra ортасында түсіндіруге арналған мысалдар
- Geogebra ортасында оқушылардың шығармашылық қабілетін арттыруға арналған мысалдар
- Geogebra ортасында кеңістіктік фигураларды салу
Мектеп оқушыларының кеңістікті қабылдап, оны көз алдына елестете алуы стереометрияны оқытудың негізгі мәселелерінің бірі болып саналады. Осы айтылған мақсатты іс жүзіне асыруда кеңістіктегі салуға берілген есептерді шешудің зор мәні бар. Геометриялық салулар теориясы - салуды негіздеу, есептерді кластарға жіктеу, есеп шешу әдістері, белгілі бір класқа жататын есептерді шешу критерийі, салу есептерін шешкенде барынша жай әдістерді тиімді қолдану сияқты мәселелерді қарастырады.
Салу есебіне талдау жасағанда сызба басты рөл атқарады. Сонда есеп шартын, сызбадағы элементтердің өзара орналасуына барынша басынан аяғына дейін талдау жасалады, есеп шартында берілгендер мен іздеген элементтер арасында байланыс орнатылады.
Мысалы, кубқа іштей және сырттай сфера салу. Бұл салуды орындау үшін «Geogebra»-ны ашып, 3D Grapher-ді басу арқылы Кеңістік алаңын ашамыз да Куб құралын таңдап Кеңістік алаңында А және В екі нүктелерін белгілейміз. Сонда белгіленген екі нүкте табанының нүктелері болатын куб тұрғызылады.
Енді Екі нүкте арқылы жүргізілген вектор құралын таңдап, А нүктесін және жазықтықта кез-келген жерден нүкте белгілейміз, ол I нүктесі болсын. Вектор бойынша объектіні көшіру құралын таңдап, Алгебра терезесіндегі а және u белгілерін бір реттен шертеміз. Сол кезде екінші куб пайда болады.
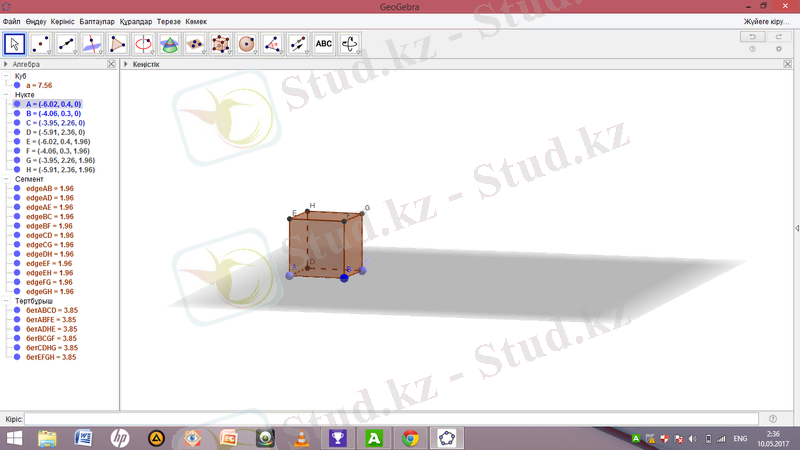
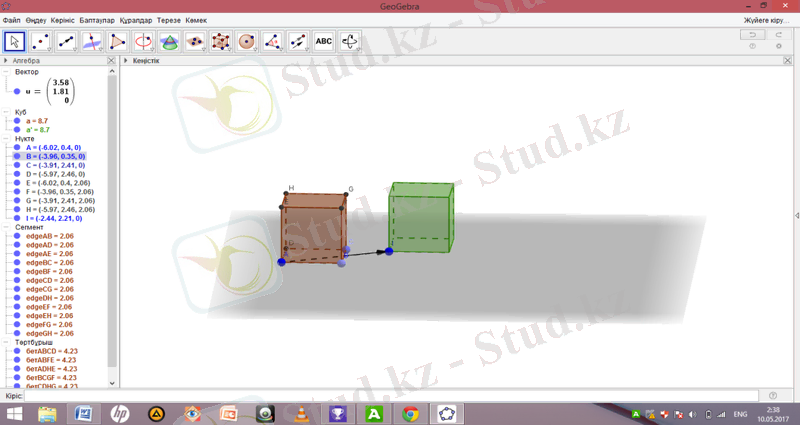
- Кубқа іштей және сырттай сфера салу
Кубтың ішінде сфера салу үшін Орта нүктесі немесе центр құралын таңдап, А және G нүктелерін бір реттен шерткенде J нүктесі және Е және G нүктелерін шерткенде К нүктесі пайда болды. Центр мен бетіндегі нүкте арқылы сфера құралын таңдап J және К нүктелерін шерту арқылы кубтың ішінде сфера салуға болды.
Алгебра терезесіндегі J және u белгілерін шерткенде екінші кубтың ішінде J ′ нүктесін салып, Центр мен бетіндегі нүкте арқылы сфера құралының көмегімен екінші кубтың ішіндегі J ′ нүктесі мен I нүктелерін шертеміз. Сонда сфераның ішінде куб пайда болады.
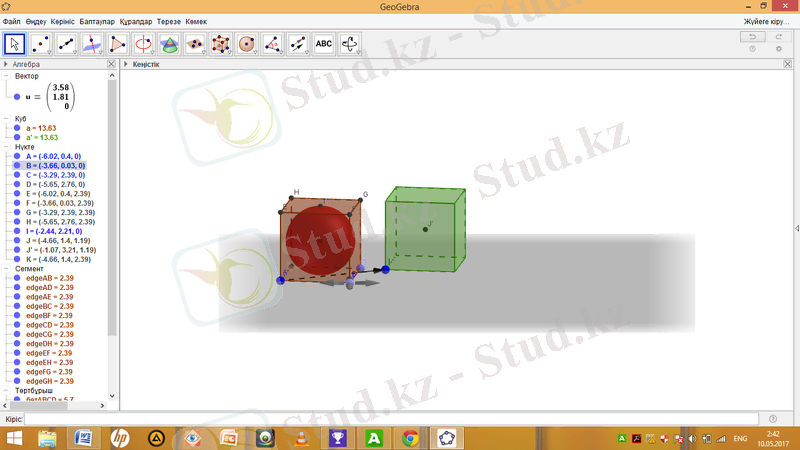
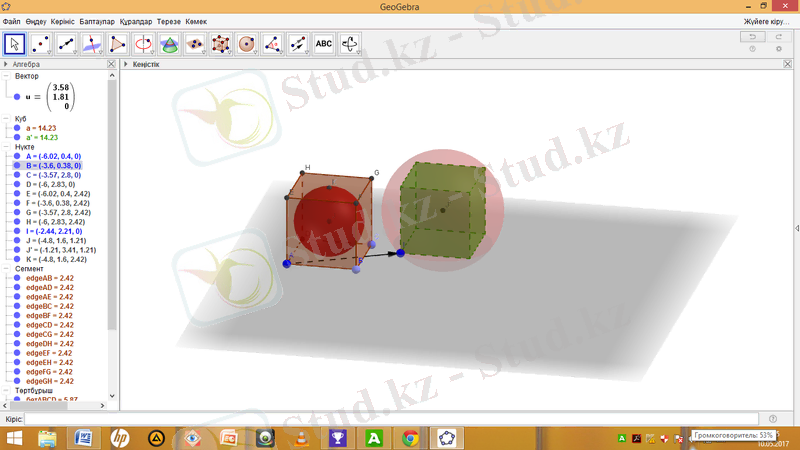
Алгебра терезесіндегі вектордың u белгісін өшіру арқылы көмекші бағыттауышты алып тастауға болады. Сонда кубқа іштей және сырттай сфера салу есебі аяқталады. Енді оны Жылжыту құралын таңдап түрлі бағытта жылжытып көруге болады.
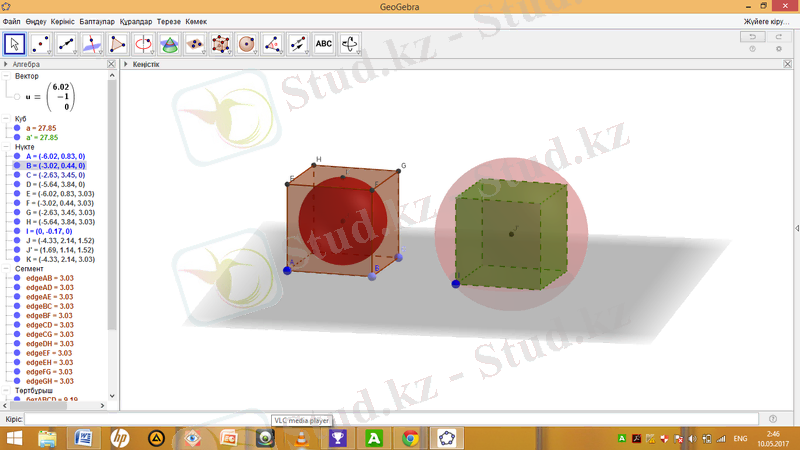
- Кубқа іштей көпбұрыш салу
Енді кубқа іштей көпбұрыш салу есебін қарастырайық.
« Куб » құралын таңдау арқылы, А және В нүктелерін белгілеп кубты салып аламыз.
« Екі нүкте арқылы түзу жүргізу » құралын таңдап, А және G нүктелерін басу арқылы түзу пайда болады.
« Бір нүкте » құралын таңдап G нүктенің жоғарғы жағынан J нүктесін белгілеп аламыз.
« Бір нүкте мен оған перпендикуляр түзу» құралын таңдап J нүктесін және жоғарғы жағынан бір нүктені басу арқылы кубты қиятын жазықтық пайда болдыртамыз.
« Екі жазықтықты қиятын қисық салу » құралын таңдап «Алгебра» терезесінде куб пен жазықтықты шертеміз, кубтың ішінде көпбұрыш пайда болады және жазықтықты жасыру құралымен жасырып қоямыз.
« Алгебра » терезесінде көпбұрышқа тышқанды апарып, оң жағын басып, 2D көріністі поли 1 бастан жасауды басамыз.
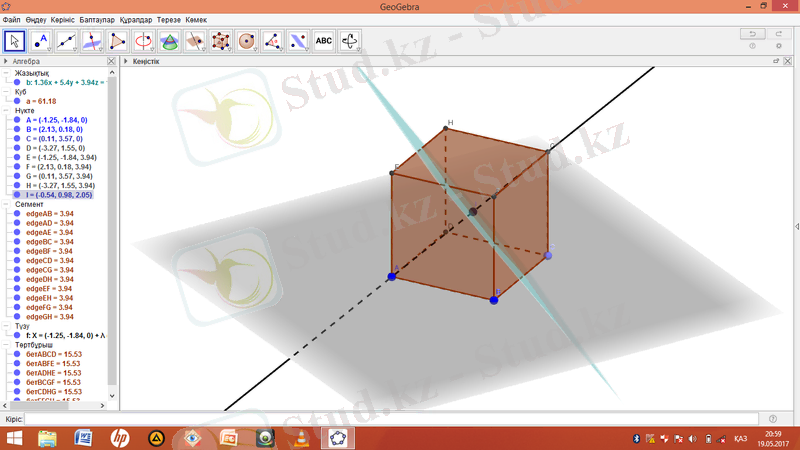
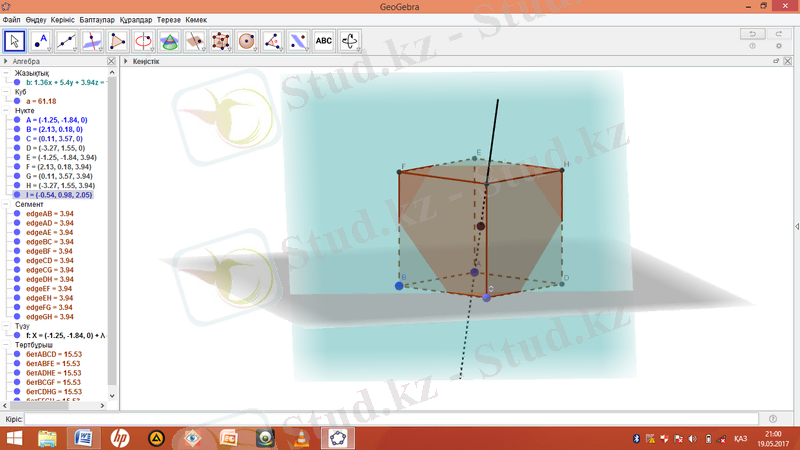
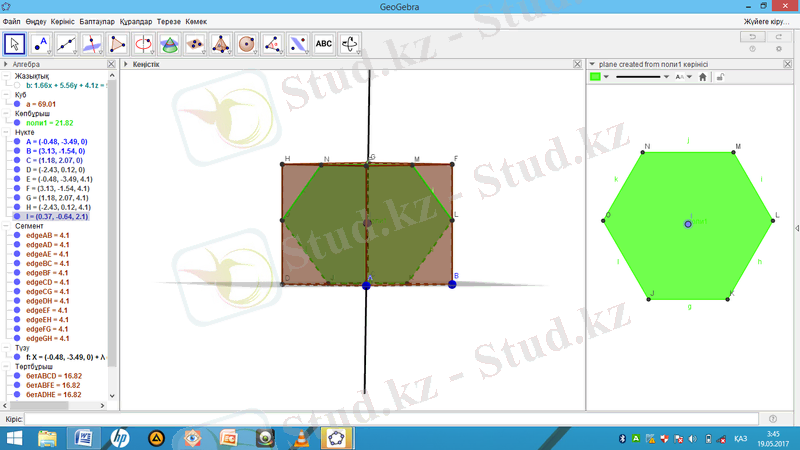
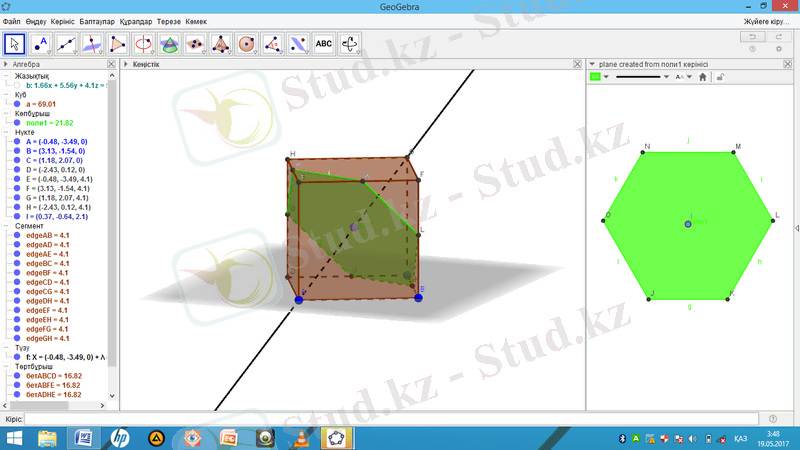
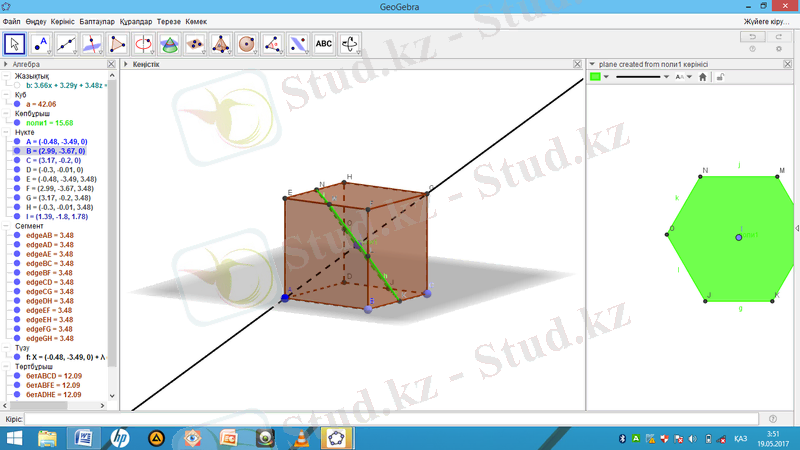
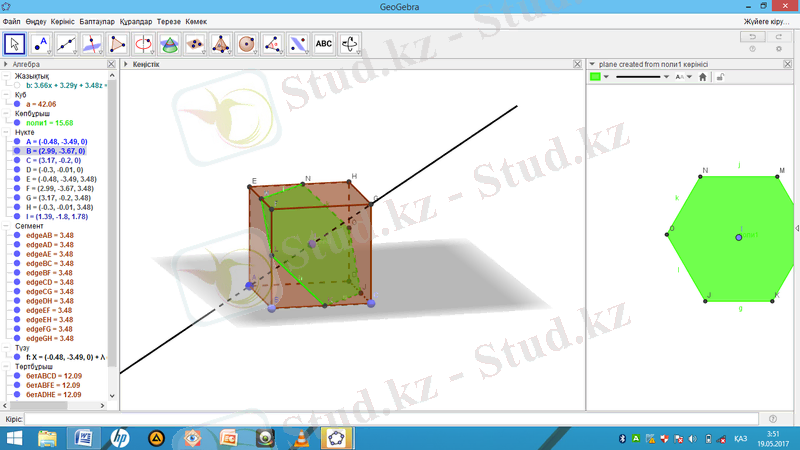
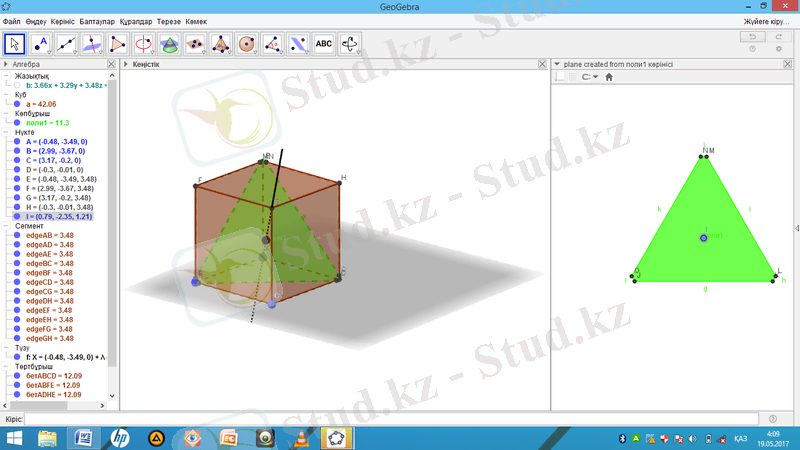
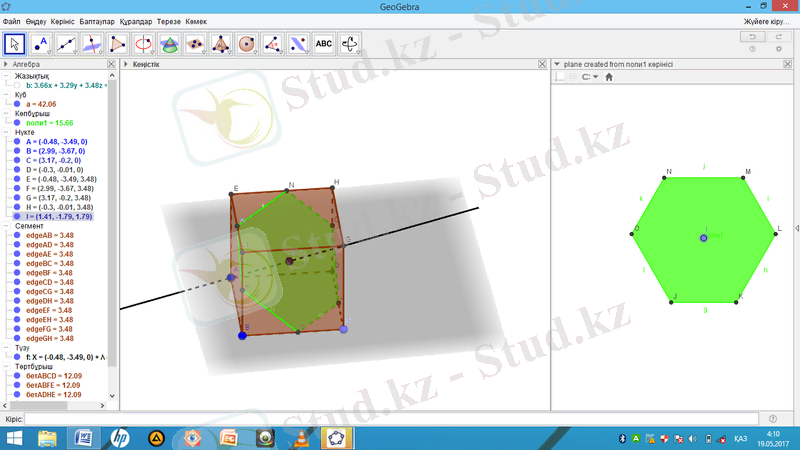
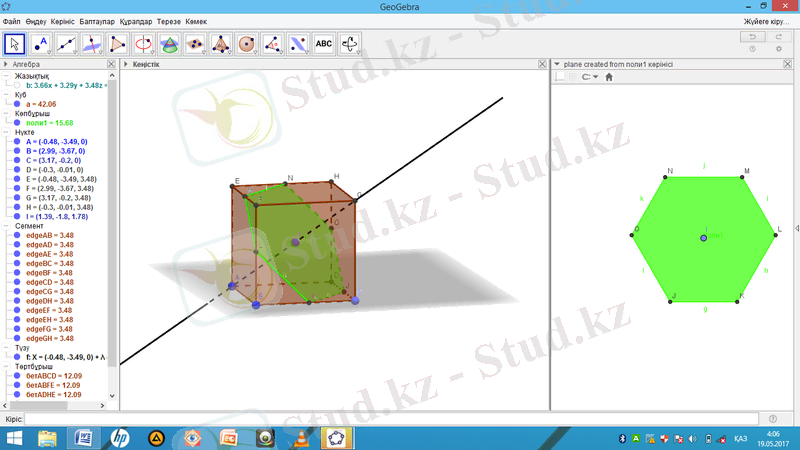
Кубқа іштей көпбұрыш салу
Кеңістік фигураларының қимасын салу есептеріне мысалда.
- Тетраэдрге қима жүргізу
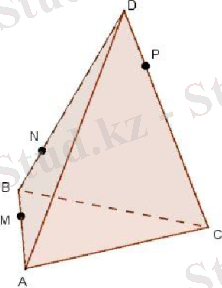
ABCD тетраэдрының AB, BC және CD қырларында M, N және P нүктелері белгіленген. Тетраэдрдың MNP жазықтығымен жүргізілген қимасын салыңыз.
Шешуі: Алдымен MNP жазықтығы ABC бетінің жазықтығымен қиылысатын түзу салу керек. М нүктесі осы жазықтықтардың ортақ нүктесі болады. Тағы бір ортақ нүктесін салу үшін NP және BC кесінділерін бір нүктеде қиылысқанша созамыз, қиылысу нүктесін Е деп белгілейміз. Е нүктесі MNP және ABC жазықтықтарының екінші ортақ нүктесі болады. Сондықтан бұл жазықтықтар МЕ түзуі бойымен қиылысады. МЕ түзуі АС қырын қандай да бір Q нүктесінде қияды. Пайда болған MNPQ төртбұрышы - ізделінді қима.
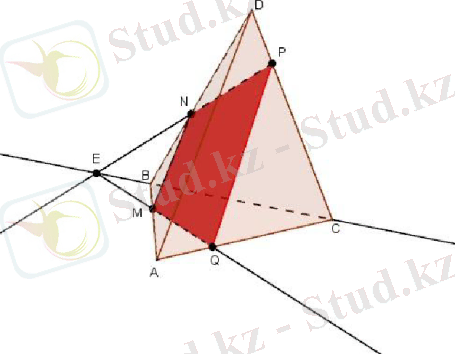
- Параллелепипедке қима жүргізу
Параллелепипедтің қырларында A, B және C нүктелері белгіленген. Параллелепипедтің ABC жазықтығы бойынша жүргізілген қимасын салыңыз.
Шешуі: Ізделінді қима A, B және C нүктелерінің параллелепипедтің қай қырларында жататындығына байланысты. Кейбір ерекше жағдайларды қарастырайық. Егер A, B және C нүктелері бір төбеден шығатын қырларда жататын болса, AB, BC және CA кесінділерін жүргізсек, онда ізделінді қима АВС үшбұрышы болады (сурет а) . Егер A, B және C нүктелері (сурет б ) көрсетілгендей орналасатын болса, онда алдымен АВ және ВС кесінділерін жүргізіп, А нүктесі арқылы АВ-ға парллель жүргіземіз. Осы түзулердің төменгі қырлармен қиылысуы Е және D болады. ЕD кесіндісін жүргізетін болсақ, онда ізделінді қима ABCDE бесбұрышы болады. Бұдан күрделі жағдай егер A, B және C нүктелері (сурет в ) көрсетілгендей орналасатын болса, онда қима жазықтық табан жазықтығымен қиылысатындай түзу жүргіземіз. Ол үшін АВ түзуімен төменгі қырын М нүктесінде қиылысатындай етіп созамыз. М нүктесі арқылы ВС-ға параллель түзу жүргіземіз. Осыдан қима жазықтығы мен төменгі табан жазықтығы қиылысатын түзу пайда болады. Бұл түзу төменгі табанының қырларымен E және F нүктелерінде қиылысады. Енді Е нүктесі арқылы АВ-ға параллель түзу жүргізейік, бұдан D нүктесін аламыз. Сонымен, AF және CD кесінділерін жүргізіп, ізделінді қима - ABCDEF алтыбұрышын аламыз.
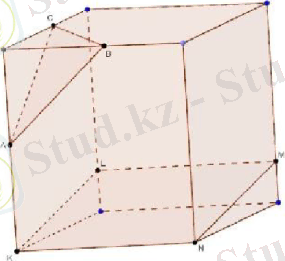
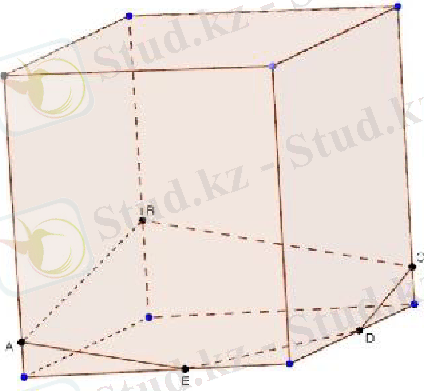
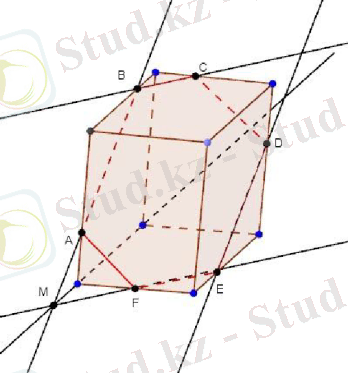
а) б) в)
«Geogebra»-ның геометриялық мүмкіндіктерін пайдаланып, мектеп геометриясынан жазықтықтағы және кеңістіктегі салу есептерін шешу әдістерін кейінгі тақырыптарда қарастырамыз.
- Дұрыс пирамидаға сырттай конус салу
«Geogebra» бағдарламасының көмегімен дұрыс пирамидаға сырттай конус салу есебін қарастырайық.
Командалар тізбесінің сипатталуы




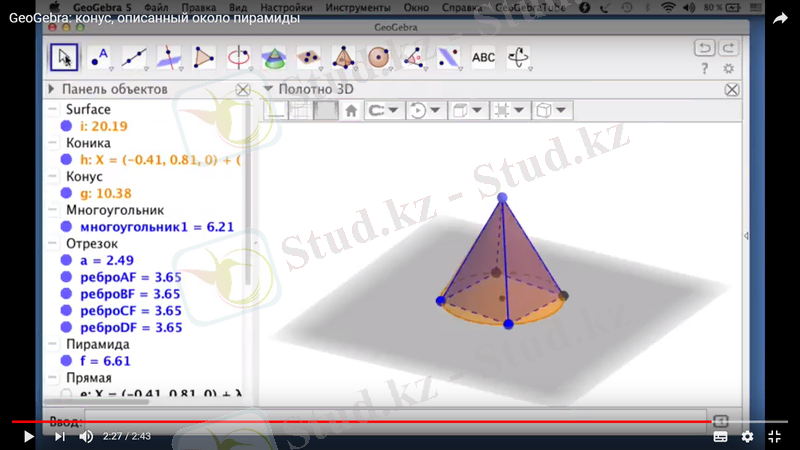
- Пирамидаға қима салу
Пирамидаға қима салу есебін «Geogebra» бағдарламасының көмегімен орындау.
Командалар тізбесінің сипатталуы.










Командалар орындалып болған соң «Geogebra» алаңында төмендегідей кескін пайда болады. Пирамида мен қималарды әр түрлі түске бояған жөн. Сонда қималар ақын көрініп тұрады.
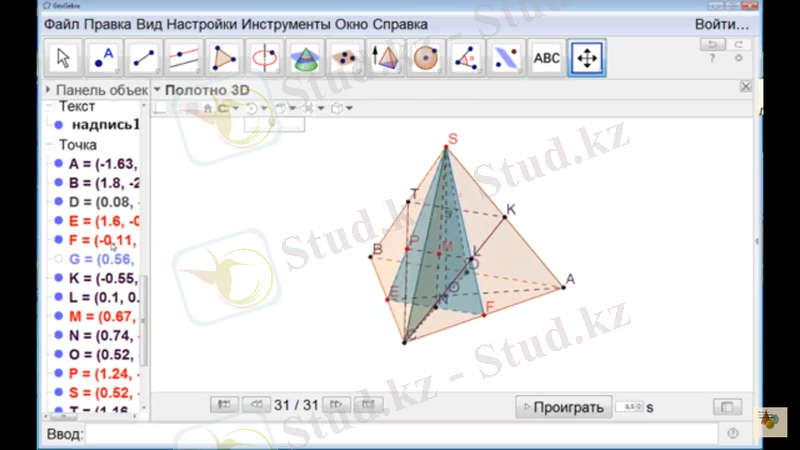
Пирамидаға қима салуды мектеп оқушылары 10-сыныпта өтеді. Сабақ барысында бағдарламаның көмегімен қима салуды көрсетуге болады.
- Кеңістіктік фигураларды анимациялау.
1-мысал. Кубтың жазбасын алу есебі. Экран бетіне салынған кубтың жазбасын алу әрекеттерін орындайық (кесте 9) .
Командалар тізбесінің сипатталуы.



Командаларды орындағаннан кейін экранда кубтың жазбасының кескіні көрінеді. Слайдерді басып оны анимацияға қойғанда кубтың жазбасы автоматты түрде ашылады және жабылады.
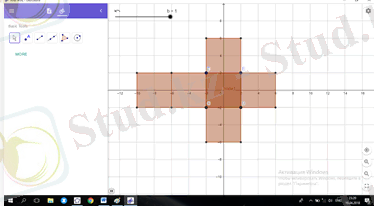
Кубтың ашылуының көрінісі.
Кубтың жазбасын оқушыларға тақтада сызып көрсету қиын. Ал бағдарламаның оны анимациялап көрсету мүмкіндігі бар.
2-мысал. «Geogebra» бағдарламасының көмегімен призманың бөлінуін көрсетейік.
Командалар тізбесінің сипатталуы.




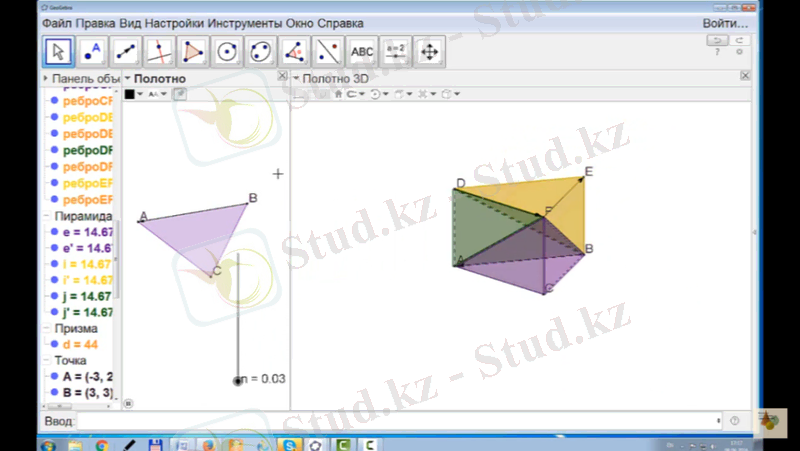
Кесінді құралын таңдап, A және F, F және B, D және B
нүктелерін қосу. Слайдер құралын таңдау. Анимацияға қою.
Жоғарыдағы командаларды орындап болған соң, Слайдердің көмегімен анимацияға қойылады. Сонда салынған призманың автоматты түрде үшке бөлінетіні және қайта орнына келетіні көрініп тұрады.
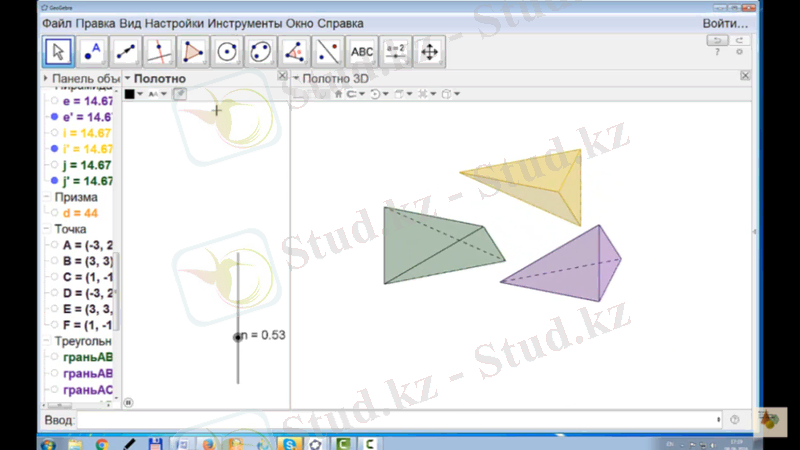
- Стереометрияның есептерін Geogebra ортасында түсіндіруге арналған мысалдар
Кеңістіктегі салу есептерін «Geogebra» бағдарламасын қолданып шешіп көрейік.
1-мысал. «Geogebra» бағдарламасының көмегімен ABCDEA 1 B 1 C 1 D 1 E 1 призмасын құру.
Командалар тізбесінің сипатталуы

Призма функциясын таңдап координат осінде 5 нүктені
таңдаймыз.

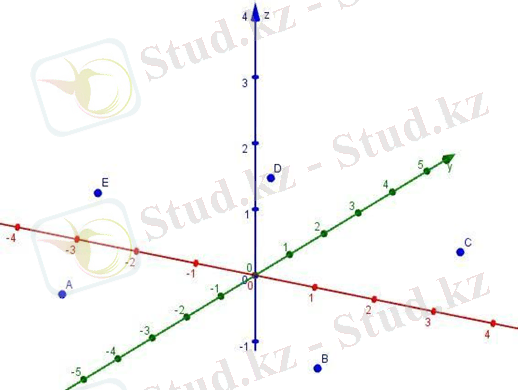
а
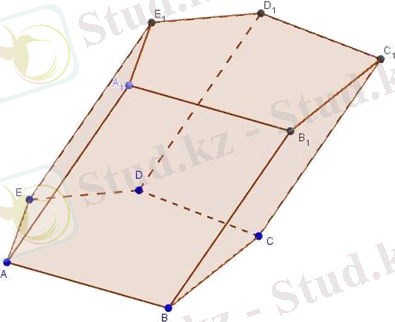
В
2-мысал . «Geogebra» бағдарламасы арқылы SABCDE пирамидасын құру
Командалар тізбесінің сипатталуы
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz