Geogebra-ның геометриялық ортасын қолданып дәлелдеуді оқыту

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 4 бет
Таңдаулыға:

14-Лекция

Лекция тақырыбы: Geogebra-ның геометриялық ортасын қолданып дәлелдеуді оқыту

Жоспар:

Сыбайлас бұрыштардың қосындысы 1800-қа тең екенін дәлелдеу.
Бұрыштың жақтарында тең кесінділер белгіленген АВ=АС. Оның биссектрисасынан D нүктесін белгілеп, алынған ABD және ACD үшбұрыштарының тең екенін көрсету.
Берілген екі параллель түзуді үшінші бір түзумен қиғанда пайда болған айқас бұрыштардың тең екенін және керісінше ұйғарымды дәлелдеу.
Үшбұрыштың бұрыштарының қосындысы жайлы теореманың дәлелдеуін анимациялық сүйемелдеу.
Пифагор теоремасының дәлелдеуін Geogebra-да көрсету

Сыбайлас бұрыштардың қосындысы 1800-қа тең екенін дәлелдеу.

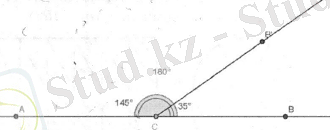
Берілгені: $\mathbf{\angle}$ BCB’ және $\mathbf{\angle}$ B’СА - іргелес бұрыштар

Дәлелдеу керек: $\mathbf{\angle}$ BCB’ + $\mathbf{\angle}$ B’СА = 180 ⁰

Компьютерлік эксперимент әдісімен негіздеу.

Эксперимент мақсаты - $\mathbf{\angle}$ BCB’ + $\mathbf{\angle}$ B’СА қосындысының бұрыштардың шамасына тәуелсіз екенін тескеру.

Динамикалық кескінді салу.

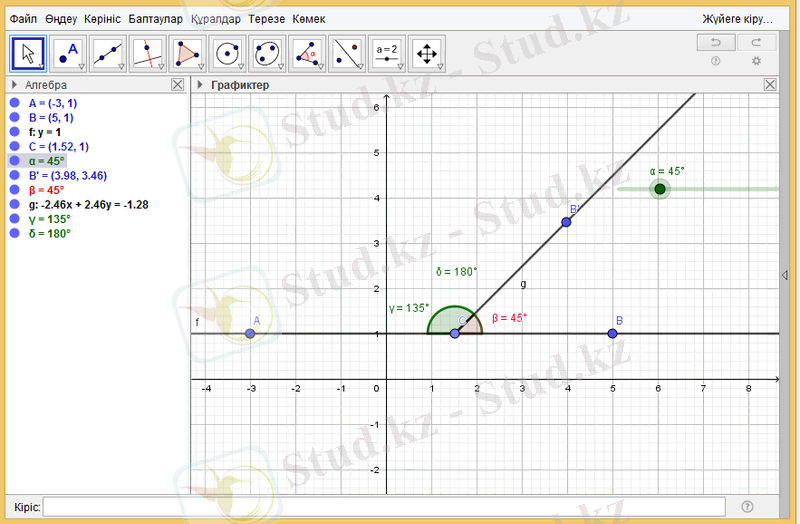
Эксперимент барысы. Слайдер арқылы α бұрышының шамасын өзгерте отырып, бұрыштардың шамасының өзгеруін және қосындының сақталуын бақылаймыз.

Қорытынды. $\mathbf{\angle}$ BCB’ + $\mathbf{\angle}$ B’СА қосындысы барлық өзгеріс кезінде 180 ⁰ -қа тең.

Бұрыштың жақтарында тең кесінділер белгіленген АВ=АС. Оның биссектрисасынан D нүктесін белгілеп, алынған ABD және ACD үшбұрыштарының тең екенін көрсету.

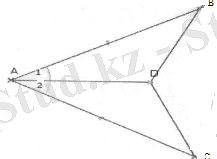
Динамикалық кескінді салу.

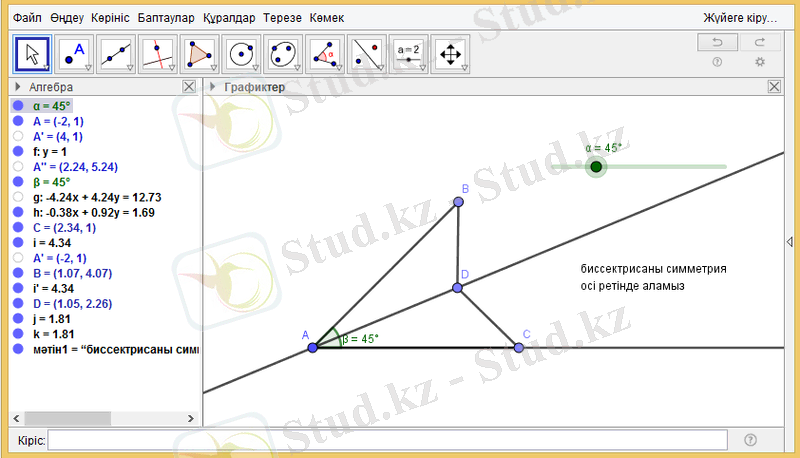
Слайдерді жылжыту арқылы түрлі жағдайда төмендегідей кескіндерді аламыз.

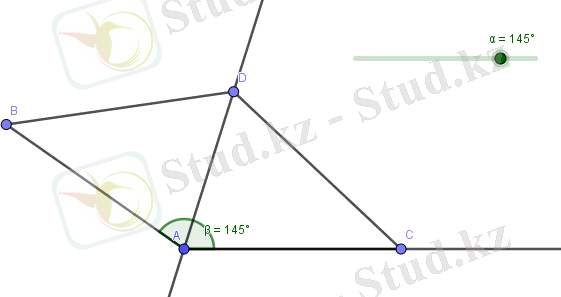
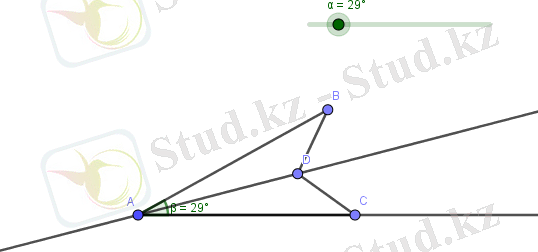
Қорытынды. ABD және ACD үшбұрыштары биссектриса түзуіне қарағанда симметриялы түрлендірулермен байланысқан нүктелер арқылы құрылғандықтан, үшбұрыштардың барлық қабырғалары тең, яғни үшбұрыштардың теңдігінің үшінші белгісі бойынша олар тең.

Берілген екі параллель түзуді үшінші бір түзумен қиғанда пайда болған айқыш бұрыштардың тең екенін және керісінше ұйғарымды дәлелдеу.

Берілгені: аb

$\mathbf{\angle}$ F және $\mathbf{\angle E}$ - ішкі айқыщ бұрыштар

Дәлелдеу керек: $\mathbf{\angle}$ F және $\mathbf{\angle E}$

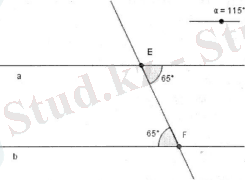
Динамикалық кескінді салу

Дәл осылай керісінше ұйғарымды да дәлелдеуге болады.

Үшбұрыштың бұрыштарының қосындысы жайлы теореманың дәлелдеуін анимациялық сүйемелдеу.

«Geogebra» бағдарламасында теоремаларды дәлелдеп көрсетуге болады . Мысалы үшін, үшбұрыштың ішкі бұрыштарының қосындысы 180 ֯ -қа тең екенін дәләлдеп көрейік.

Командалар тізбесінің сипатталуы.

№

Құралдар

Орындалатын іс-әрекеттер

№: 1

Құралдар:

Орындалатын іс-әрекеттер: «Geogebra» бағдарламасын ашу

№: 2

Құралдар:

Орындалатын іс-әрекеттер: Екі нүкте арқылы түзу жүргізу

№: 3

Құралдар:

Орындалатын іс-әрекеттер: Жаңа нүкте

№: 4

Құралдар:

Орындалатын іс-әрекеттер: Көпбұрыш

№: 5

Құралдар:

Орындалатын іс-әрекеттер: АВС үшбұрышы пайда болды.

№: 6

Құралдар:

Орындалатын іс-әрекеттер: Бұрыш таңдаймыз. Бұрыштардың градустық өлшемдері шығады.

№: 7

Құралдар:

Орындалатын іс-әрекеттер: Бұрыштарды әртүрлі түс қылған жөн.

№: 8

Құралдар:

Орындалатын іс-әрекеттер: Слайдермен α және β бұрыштарын таңдаймыз.

№: 9

Құралдар:

Орындалатын іс-әрекеттер: Орта нүктесі немесе центрді таңдаймыз.

№: 10

Құралдар:

Орындалатын іс-әрекеттер: Обьектіні бір нүктенің айналасында бұрыш арқылы айналдыру

№: 11

Құралдар:

Орындалатын іс-әрекеттер: Сағат тіліне кері бағытта айналдырамыз.

№: 12

Құралдар:

Орындалатын іс-әрекеттер: Бұрыштарды анықтау үшін жылжыту құралымен үшбұрышты таңдаймыз, сонда бұрыштардың градустық өлшемі көрінеді.

№: 13

Құралдар:

Орындалатын іс-әрекеттер: Енді слайдерді жылжытқанда үшбұрыштың ішкі бұрыштарының қосындысы 180 ֯ -қа тең екенін көреміз.

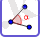
Сурет 1- Үшбұрыштың ішкі бұрыштарының қосындысы $180{^\circ}$ -қа теңдігінің көрінісі

Бұл кескінде үшбұрыштың ішкі бұрыштарының қосындысы $180{^\circ}$ -қа тең екендігі көрсетілген. Теорема: «Кез келген үшбұрыш үшін оның ішкі бұрыштарының қосындысы $180{^\circ}$ -қа тең». Бағдарламаны пайдаланып кез келген үшбұрыш салып, сол үшбұрышты екі нүктесінен айналдырамыз. Олай болса, кескінде көрсетілген бұрыш мәндерін есептеп теореманың дұрыстығына көз жеткізуге болады.

Осы көріністің анимациялық сүйемелдеуін келесі кескіндерден көруге болады .

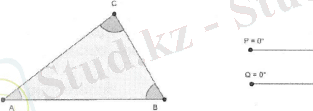
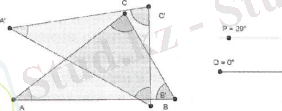
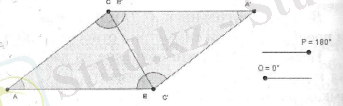
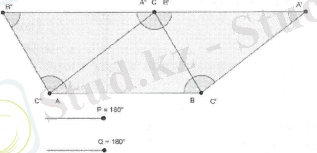
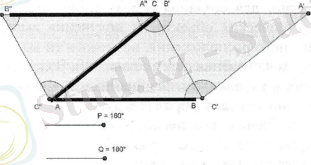
С нүктесі арқылы АВ-ға параллель екі түзу жүргізілгендіктен, В", С және А ' нүктелері бір түзудің бойында жатады. Демек, В"СА' бұрышы - жазыңқы, олай болса үшбұрыштың бұрыштарының қосындысы 180°тең.

Пифагор теоремасының дәлелдеуін Geogebra-да көрсету

Динамикалық кескінді салу.

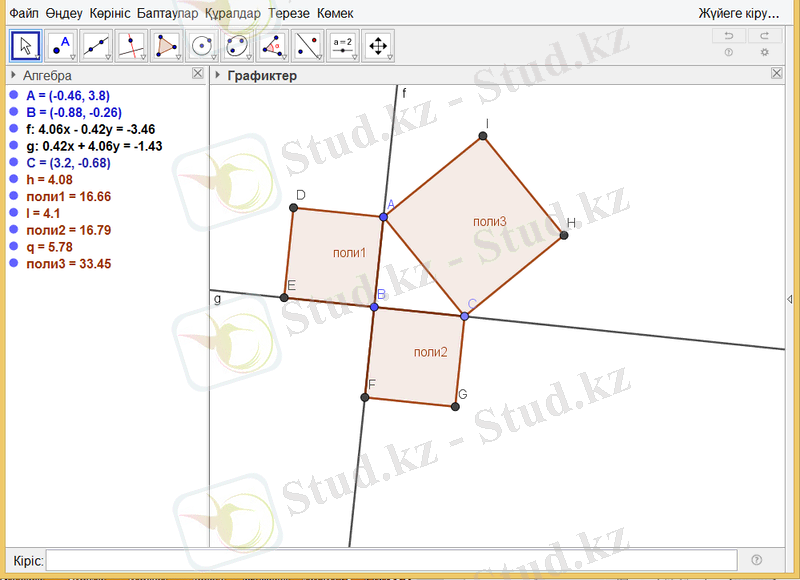
Сурет 2 - Пифагор теоремасын дәлелдеуден көрініс

Үшбұрыштың қабырғаларына түсірілген квадраттың аудандары алгебра бөлімінде көрсетілгендей поли1= 16, 66; поли2=16, 79; поли3=33, 45. Бұдан поли3= поли1+ поли2 екенін көруге болады. Үшбұрыштың төбелерін жылжыту арқылы барлық жағдайда поли3= поли1+ поли2 болатынын байқауға болады. Мұндай эксперимент арқылы пифагор теоремасының тұжырымдамасын жасаймыз.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.