Бөлшек сандарды оқыту әдістемесі: жай және ондық бөлшектер, қасиеттері мен амалдары


 2-лекция
2-лекция
Бөлшек сандарды оқыту
Жоспары:
1. Бөлшек сандарды оқыту реті туралы.
2. Жай бөлшек ұғымын енгізу. Жай бөлшектің қасиеттері. Жай бөлшектің түрлері.
3. Жай бөлшектерге амалар қолдану.
4. Ондық бөлшек ұғымын енгізізу.
5. Ондық бөлшектерге амалдар қолдануға үйрету.
Әдебиеттер:
1. Рахымбек Д. А рифметика, алгебра, анализ бастамаларын оқыту әдістемесі. /Оқулық/ - Шымкент: М. Әуезов атындағы ОҚМУ баспа орталығы 2016. - 432 б
2. Рахымбек Д. Мектепте сандық жүйені оқыту әдістемесі: Оқу құралы. /Д. Рахымбек. - Шымкент: ОҚМПУ, 2020. - 98 бет.
3. Елубаев С. Математиканы оқыту әдістемесі. - Алматы; Эверо, 2016
4. Мектеп оқулықтары
5. Мұғалімге арналған оқу-әдістемелік құралдар
1. Жай бөлшек ұғымын енгізу. Жай бөлшек ұғымын енгізудің қажеттілігі.
 ,
,
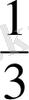 ,
,
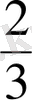 , …. жай бөлшектерiмен алғашқы рет танысу бастауыш сыныпта натурал сандарды оқытумен параллель жүргiзiледi. Бастауыш мектеп оқушылар санның бөлігін, бөлігі бойынша санды табу есептерін шығара алады.
, …. жай бөлшектерiмен алғашқы рет танысу бастауыш сыныпта натурал сандарды оқытумен параллель жүргiзiледi. Бастауыш мектеп оқушылар санның бөлігін, бөлігі бойынша санды табу есептерін шығара алады.
Бөлшектердi жүйелi түрде оқыту 5-сыныпта басталады. Алдымен жай бөлшектер және оларға амалдар қолдану‚ одан соң ондық бөлшек тақырыбы оқып-үйретiледi. Ондық бөлшектер жай бөлшектермен салыстырғанда жаңа сандар емес. Олар оқушыларға бұрыннан таныс, бөлiмдерi 10, 100, 1000 және т. с. с. болып келген жай бөлшектердiң өзгеше түрде жазылу көрiнiсi ғана. Математикалық есептеулер мен практикалық есеп-қисапта ондық бөлшектердi пайдаланған анағұрлым ыңғайлы. Жай бөлшектер практикалық есептеулерде ондық бөлшектерге қарағанда әлдеқайда аз қолданылады.
ЭЕМ ондық бөлшектермен ғана жұмыс iстейдi.
Осыған байланысты математиканы оқыту әдiстемесiнде жай бөлшектер мен ондық бөлшектердi оқытудың тәртiбi туралы мәселе туындайды. Осы мәселені шешудiң мүмкiн болатын тәсiлдерiне тоқталып өтейiк:
- алдымен жай бөлшектер, одан кейiн барып ондық бөлшектер оқытылады (дәстүрлi әдiс) ;
- алдымен ондық бөлшектер, кейiннен барып жай бөлшектер оқытылады;
- жай бөлшектер мен оңдық бөлшектердi оқыту аралас жүргізіледі.
Қазіргі мектеп бағдарламасы бойынша «Математика-5» сынып оқулығында алдымен жай бөлшектер, одан кейiн пайыз бен пропорциялар, кейiн ондық бөлшектер оқытылады.
Ал Н. Я. Виленкиннiң «Математика-5» оқулығында алдымен жай бөлшектер ұғымы енгiзiледi. Содан кейiн бөлшектердi салыстыру, бөлiмдерi бiрдей бөлшектердi қосу және азайту амалдары оқытылады. Бұдан кейiн ондық бөлшектерге өту және оларға қолданылатын төрт амал қарастырылады. Ондық бөлшектердi оқыту 5-сыныпта басталып, сонда аяқталады. Бұдан кейiн 6-сыныпта жай бөлшектердi оқуға қайта оралады: кез келген бөлшектердi салыстыру және оларға арифметикалық амалдар қолдану оқып үйретiледi. Ондық бөлшек ұғымына процент ұғымы қабаттасып оқытылады. Процент бөлiмдерi 100 болып келген ондық бөлшектердiң жаңа формадағы жазылуы болып табылады:
1% =
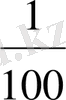 =0, 01; 15%=
=0, 01; 15%=
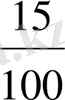 =0, 15 және т. с. с
=0, 15 және т. с. с
Казіргі метеп оқулықтарында жай бөлшектер тақырыбы толық оқып-үйренілгеннен кейін ондық бөлшекке өтеді.
1. 3. 1 Жай бөлшек ұғымын енгізу
«Бөлшек сандар» тақырыбындағы ең негiзгi ұғым жай бөлшек болып табылады. Ол сипаттамалық түрде былай енгiзiледi: теңдей етiп 4-ке бөлiнген алманың суретi қарастырылады. Олардың бiреуi бiр тәрелкеге, ал қалған үшеуi басқа тәрелкеге салынады және былай дейдi: «Бiрiншi тәрелкеде алманың төрттен бiр бөлiгi, ал екiншiсiнде алманың төрттен үш бөлiгi жатыр». Мұны былай жазады: «
 алма,
алма,
 алма». Бұдан кейiн мұндай
алма». Бұдан кейiн мұндай
 және
және
 сандарының жай бөлшектер деп аталатыны хабарланады. Және олар сәйкес «төртен бір», «төрттен үш» дкеп оқылатына айтылады.
сандарының жай бөлшектер деп аталатыны хабарланады. Және олар сәйкес «төртен бір», «төрттен үш» дкеп оқылатына айтылады.
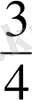 бөлшегiнде 3 саны бөлшектiң алымы, ал 4 саны оның бөлiмi деп аталады. Бөлшектiң бөлiмi заттың (нәрсенiң) теңдей етiп қанша бөлiкке бөлiнгенiн, ал алымы сондай бөлiктен қаншасы алынғандығын көрсетедi. Алымын бөлшек сызығының үстiне, ал бөлiмiн оның астына жазады. Осындай түсiндiрулер басқа да мысалдар арқылы қайталанады. Алманың орнына теңдей етiп, төртке (сегiзге, алтыға, он екiге) бөлiнген дөңгелектi, (кесiндiнi, тiктөртбұрышты, квадратты) алуға болады.
бөлшегiнде 3 саны бөлшектiң алымы, ал 4 саны оның бөлiмi деп аталады. Бөлшектiң бөлiмi заттың (нәрсенiң) теңдей етiп қанша бөлiкке бөлiнгенiн, ал алымы сондай бөлiктен қаншасы алынғандығын көрсетедi. Алымын бөлшек сызығының үстiне, ал бөлiмiн оның астына жазады. Осындай түсiндiрулер басқа да мысалдар арқылы қайталанады. Алманың орнына теңдей етiп, төртке (сегiзге, алтыға, он екiге) бөлiнген дөңгелектi, (кесiндiнi, тiктөртбұрышты, квадратты) алуға болады.
Осы баяндауға сәйкес жай бөлшектердi енгiзудiң әдiстемелiк схемасы мынадай болады:
1) қарастырылатын затты теңдей етiп бірнеше бөлікке, біздің жағдайымызда 4 бөлiкке бөлу;
2) «төрттен бiр», «төрттен үш» терминдерiн хабарлау;
3)
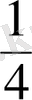 ,
,
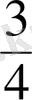 жазуларын енгiзу;
жазуларын енгiзу;
4) «жай бөлшек», «бөлшектiң алымы», «бөлшектiң бөлiмi» терминдерi ненi көрсететiнiн айту;
5) бөлшектiң басқа мысалдарын келтiру, оларды оқу және жазу.
Бөлшек сандарды оқыту әдiстемесiнiң аса маңызды элементi жаңа сандарды енгiзу қажеттiлiгiне оқушылардың көзiн жеткiзу болып табылады. Оқушыларды сендiрудiң тағы бір жолы санның үлестерiн жазуда мұндай бөлшектердiң аса пайдалы екендiгiн түсiндiру. Бөлшек сандарды енгiзу қажеттiгiн оқушыларға былай түсiндiруге болады: Натурал сандар жиынында 2 саны 3 санына бөлiнбейдi. Бiрақ натурал сандарды бөлу амалы бөлшек сандар арқылы әрқашан орындалады. Натурал сандар жиыны бөлшектермен толықтырылады. 2-нi 3-ке бөлу амалын қарастырайық. 2 алманы 3 оқушыға тең бөлу қажет болсын. Мұны қалай орындауға болады? Әрбiр алманы теңдей етiп 3 бөлiкке бөлемiз. Сонда мұндай бөлiктiң бiрi
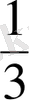 бөлшегi арқылы өрнектеледi. Егер әрбiр оқушыға осыны екi бөлiктен беретiн болса, онда 2 алма 3 оқушыға теңдей етiп бөлiнген болады. Бiр алманың екi бөлiгi
бөлшегi арқылы өрнектеледi. Егер әрбiр оқушыға осыны екi бөлiктен беретiн болса, онда 2 алма 3 оқушыға теңдей етiп бөлiнген болады. Бiр алманың екi бөлiгi
 бөлшегi арқылы өрнектеледi. Олай болса, әрбiр оқушы алманың
бөлшегi арқылы өрнектеледi. Олай болса, әрбiр оқушы алманың
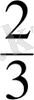 бөлiгiн алады, яғни 2:3=
бөлiгiн алады, яғни 2:3=
 .
Мынадай қорытынды жасалынады:
ендi 2 натурал санын 3 натурал санына бөлуге болады, бөлу нәтижесiнде натурал сан емес, бөлшек сан
.
Мынадай қорытынды жасалынады:
ендi 2 натурал санын 3 натурал санына бөлуге болады, бөлу нәтижесiнде натурал сан емес, бөлшек сан
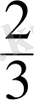 шығады.
шығады.
Бөлшек сандарды енгiзу қажеттiлiгiнiң тағы бiр жолы ол шамаларды өлшеуге байланысты. Айталық, ұзындығы 1 см-ден кiшi кесiндiнi см-мен өлшеу қажет болсын. Оқушылар өлшеу кезiнде кесiндiнiң ұзындығының 1 см-ден кiшi екендiгiн байқайды. Мұнда милиметрдi (1мм =
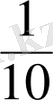 см) пайдаланған тиiмдi. Айталық кесiндiнiң ұзындығы 9 мм-ге тең болсын. Бұл кесiндiнiң ұзындығының
см) пайдаланған тиiмдi. Айталық кесiндiнiң ұзындығы 9 мм-ге тең болсын. Бұл кесiндiнiң ұзындығының
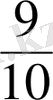 см екенiн көрсетедi. Бұдан берiлген кесiндiнiң ұзындығы сантиметрмен бөлшек сан арқылы өрнектелiп тұрғандығы көрiнедi. Демек, кесiндiнiң ұзындығын өлшеу үшiн бөлшек сандар қажет екен.
см екенiн көрсетедi. Бұдан берiлген кесiндiнiң ұзындығы сантиметрмен бөлшек сан арқылы өрнектелiп тұрғандығы көрiнедi. Демек, кесiндiнiң ұзындығын өлшеу үшiн бөлшек сандар қажет екен.
«Жай бөлшек» ұғымын енгізу барысында оқушылардан күтілетін нәтижелер:
1. Бөлшек бүтіннің немесе бірліктің тең бөліктерге бөлгендегі бөлігі екендігін біледі.
Мынадай сұрақтарға жауап бере алады.
- Бөлшек дегеніміз не?
- Бөлшектің бөлімі нені білдіреді?
- Бөлшектің бөлімінің мағнасы қандай?
2. Бөлшектің аламы мен бөлімінің мғынасын нақтылы мысалдар арқылы көрсете алады.
3. Бөлшекті оқып-жаза алады: жарты, үштен бір, ширек, үштен екі, алтыдан бес т. с. с. және оларға сәйкес жазылыулар
 ,
,
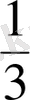 ,
,
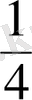 ,
,
 ,
,
 т. с. с.
т. с. с.
4. Бөлшекпен байланысты есептерді шығара алу:
1) санның бөлігін табу;
2) «берілген бөлшекке сәйкес санды табу»;
3) бір сан екінші санның қандай бөлігін құрайтындығын анықтау.
5. Натуарл сан ұғымының кеңейгенін білу: екі натурал санды бөлуге болады, бөлу нәтижесiнде натурал сан да, бөлшек сан да болуы мүмкін.
Мұндай күтілетін нәтижелерге жету үшін жаттығулар орындап, есептер шығару керек. Мәселен Т. А. Алдамұратова мен Е. С. Байшолановтың 5 сыныпқа арналған «Математика» оқулығында [2] төмендегідей берілген.
1. Бөлшек бүтіннің немесе бірліктің тең бөліктерге бөлгендегі бөлігі екендігін білуге арналған жаттығулар: №№ 393, 402в, 413с, 398
2. Бөлшектің аламы мен бөлімінің мғынасын түсініуге жаттығулар: №394,
3. Бөлшекті оқып-жаза алу №403в, 404в
4. «Санның бөлігін табу» №410в, 411в ; «берілген бөлшекке сәйкес санды табу» №399, 400, 408в есептерін шығара алу, «бір сан екінші санның қандай бөлігін құрайтындығын анықтау» № 405в, 406в
5. Натуарл сан ұғымының кеңейгенін білу: екі натурал санды бөлуге болады, бөлу нәтижесiнде натурал сан да, бөлшек сан да болуы мүмкін. №395, 396, 397, 407в
Оқушылардың күтілген нәтижеге жеткен жетпегенін анықтауға арналған жаттығулардың бір нұсқасын келтіреміз:
- Бірнеше бөлшек жаз. Оның алымы мен бөлімі нені білідреді?
- Бөлшектің бөлімі 7 және 13 болатын төрт бөлшек жаз
- Бөлшектің алымы 5 және 8 болатын төрт бөлшек жаз.
- Бөлшектерді оқы (сөзбен жазып шық) :
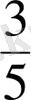 ,
,
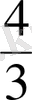 ,
,
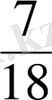 ,
,
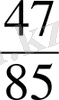 ,
,
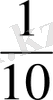 ,
,
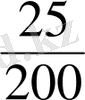 ,
,
 .
.
Бұл бөлшектерді бөлінді түрде жазып көрсет.
- Бөліндіні бөлшек түрінде жаз: 5:13; 15:4; 12:3 ; 1:1; 8:1; 7:7.
- Натурал санды бөлімі нөлден басқа болатын бөлшек түрінде жазуға болады.
- 1, 2, 3, 4, 5 сандарының әр қайсысын төрттен бөлшек түрінде жазып көрсет.
- 7 санын бөлімдері 1, 2, 7, 12, 101 болатын бөлшек түрінде жаз.
- Цифрлармен жаз:
Екіден бір (жарты), он үштен сегіз, тоқсан үштен он жеті, бір жүз жиырма бірден екі, мыңнан екі жүз сексен бес.
- 18 алма 6 оқушыға теңдей бөлініп берілді. Әрбір оқушы барлық алманың қандай бөлігін алды?
- Бір түрлі матаныңүлесі 96 теңге, ал екінші түрлі матаның-і 100 теңге тұрса, онда қайсы мата қымбат.
- 24 га жерге егін егілді. Бұл барлық егістік жердіңбөлігі. Барлық егістік жердің ауданы қандай?
- Сыныпта 28 оқушы бар. Бақылау жұмысында олардың ширегі «өте жақсы», жартысы «жақсы» және «өте жақсы», қалғандары «қанағаттанарлық» баға алды. Барлық оушылырдың қандай бөлігі «қанағаттанарлық» бағаға алды.
1. 3. 2 Жай бөлшектің қасиеті
Жай бөлшек екі натурал санның бөлiндiсі (
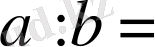
 ) ретiнде қарастырылғаннан кейiн жай бөлшектiң қасиетi оқып-үйретiледi.
) ретiнде қарастырылғаннан кейiн жай бөлшектiң қасиетi оқып-үйретiледi.
Мұғалiм тақтаға дөңгелек сызып, дөңгелектi тең төрт бөлiкке бөледi, оның бiр үлесiн жай бөлшекпен
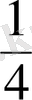 түрiнде жазады. Осындай үлестiң үшеуi жай бөлшекпен
түрiнде жазады. Осындай үлестiң үшеуi жай бөлшекпен
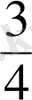 түрiнде жазылады. Ол бөлiктер бояп қойылады. Ендi осы бөлiктердiң әрқайсысын тағы да тең екi бөлiкке бөлсек, дөңгелектiң
түрiнде жазылады. Ол бөлiктер бояп қойылады. Ендi осы бөлiктердiң әрқайсысын тағы да тең екi бөлiкке бөлсек, дөңгелектiң
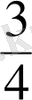 үлесi
үлесi
 үлесiне тең болады. Сонда
үлесiне тең болады. Сонда
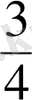 бөлшегi мен
бөлшегi мен
 бөлшектерiнiң сандық мәндерi бiрдей екенi дөңгелектердiң боялған бөлiктерiнен көрiнедi. Осы процесс керiсiнше қарастырылып,
бөлшектерiнiң сандық мәндерi бiрдей екенi дөңгелектердiң боялған бөлiктерiнен көрiнедi. Осы процесс керiсiнше қарастырылып,
 -ның
-ның
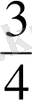 -ке тең екенi көрсетiледi. Демек,
-ке тең екенi көрсетiледi. Демек,
 =
=
 ;
;
 =
=
 .
.
Бөлшектiң алымын да, бөлiмiн де, бiр натурал санға көбейткеннен немесе бөлгеннен бөлшектiң мәнi өзгермейтiндiгi айтылады.
Берiлген жай бөлшектiң алымы мен бөлiмiндегi сандардың шамасы көп болғанда, бөлшектi жеңiлдету үшiн, бөлшектiң осы қасиетiне сүйенiп бөлшектердi қысқартудың тәсiлдерi қарастырылады. Бөлшектердi қысқарту жұмысы бөлшектiң алымы мен бөлiмi өзара жай сандар болғанда ғана аяқталады.
Алымы мен бөлiмi өзара жай сандар болатын бөлшектер қысқартылмайтын бөлшектер болатындығы мiндеттi түрде ескертiледi.
Жай бөлшектердің қасиетін оқып үйренуде оқушылардан күтілетін нәтижелер:
- Жай бөлшектің негізгі қасиетін білу.
- Егер бөлшектің алымы да бөлімі де бірдей санға көбейтсе, бөлшектің мәні өзгермейді;
- Егер бөлшектің алымы да бөлімі де бірдей санға бөлінсе, бөлшекті мәні өзгермейді.
- Бөлшектерді қысқарта алу:
- Натурал сандардың бөлінгіштік белгілерін пайдаланып тізбектей қысқарту;
- Бөлшектің алымы мен бөлімінің ең үлкен ортақ бөлгішін (ЕҮОБ) тауып бірден толық қысқарту.
- Бөлшектің не алымын, не бөлімі бір санға көбейтсе бөлшектің мәні қалай өзгеретінін білу.
- Бөлшектің бөлімін өзгертпей, оның алымын бір санға көбейтсе;
- Бөлшектің бөлімін өзгертпей, оның алымын бір санға бөлсе;
- Бөлшектің алымын өзгертпей, оның бөлімін бір санға көбейтсе;
- Бөлшектің алымын өзгертпей, оның бөлімін бір санға бөлсе.
Жай бөлшектің негізгі қасиеттерін оқып-үйрену нәтижесінде күтілетін нәтжелерге жеткен-жетпегенін анықтауға ааранлған сұраулар мен жаттығулар.
- Белгісіздің орнына теңдік дұрыс болатындай мәндер тауып қой.
- =; 2) =; 3) =: 4) =.
- бөлшегін неше тәсілмен 6 есе кемітуге болады?
- бөлшегін неше тәсілмен 3 есе арттыруға болады?
- Мынадай сұрақтарға жауап беру:
- Бөлшектерді қысқарту қандай қасиеттерге негізделген?
- Қандай бөлшектер қысқармайтын бөлшектер?
- Бөлшентерді қысқартқан кезде не өзгереді не өзгермейді?
- Бөлшектерді
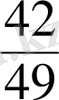 ;
;
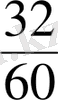 ;
;
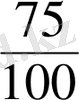 ;
;
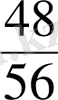 .
.
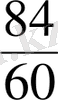 екі тәсілмен қысқарт
екі тәсілмен қысқарт
- алымы мен бөлімінің ең үлкен ортақ бөлгішін тауып;
- тізбектей.
1. 3. 3 Жай бөлшектің түрлері
Жай бөлшектiң алымы мен бөлiмiндегi натурал сандардың бiр-бiрiнен үлкен, кiшi болуына байланысты жай бөлшектер дұрыс бөлшек, бұрыс бөлшек болатыны мысалдармен түсiндiрiледi. Сонымен қатар бүтiн сан мен дұрыс бөлшектен тұратын сандар ерекше аралас сан деп аталатыны айтылады.
Бұрыс бөлшекпен берiлген санды аралас сан түрiнде жазу және керiсiнше аралас санды бұрыс бөлшекпен жазу ережелерi тұжырымдалады. Бұрыс бөлшектi аралас сан түрiнде жазу қалдықпен бөлу арқылы көрсетiледi. Оқушыларға түсiнiктi болу үшiн бұрыс бөлшектiң алымын бөлiнгiш етiп, бөлiмiн бөлгiш етiп алса, толымсыз бөлiндi - аралас санның бүтiн бөлiгi; ал қалдық алымы, бөлгiш бөлiмi етiп жазылатындығы айтылады. Бұл жағдай бөлшектерге амалдар қолдануда (бөлшектердi азайтуда) натурал сандарды бұрыс бөлшек түрiнде және аралас сан түрiнде ашып жазуда қажет.
Бөлiмдерi бiрдей екi бөлшектi салыстыруда олардың алымына тәуелдi болатындығы көрнекi түрде көрсетiледi: бөлiмдерi бiрдей бөлшектердiң алымы тең болса, тең бөлшек, ал алымы үлкенi - үлкен бөлшек.
Жай бөлшектердің түрлерін оқып үйренуден күтілетін нәтижелер:
- Қандай бөлшектер дұрыс, бөлшек, бұрыс бөлшек деп аталатындығын білу.
- Бөлшектерді ішінен дұрыс бөлшек, бұрыс бөлшектерді ажырата алу.
- Дұрыс бөлшектер 1-ден кем, бұрыс бөлшектер 1-ге тең немесе 1-ден артық болатынын білу.
- Аралас санның қандай сан екенін білу.
- Аралас санды бүтін және бөлшек бөліктерге ажырата алу.
- Аралас санды бұрыс бөлшекке айналдыра алу.
- Бұрыс бөшекті аралас сан түрінде жаза білу.
Төмендегі сұрақтарға жауап беріп, жатығулар орындай алу тиіс.
- Қандай бөлшек дұрыс бөлшек делінеді?
- Бұрыс бөлшек деген не?
- Дұрыс және бұрыс бөшектерді ажыратып жаз:
.
,
,
,
,
,
;
;
;
.
.
- ., ,, ,, ; ; ; . бөлшектерінің қайсысының міндері
- Бірден кем;
- Бірден артық;
- Бірге тең.
- Мына сұрақтарға жауап бер:
- Аралас сан деген не?
- Аралас санды бүтін және бөлшек бөліктерге қалай ажыратуға болады?
- Аралас сан бұрыс бөлшекке қалай айналдырылады?
- Бұрыс бөшекті аралас сан түрінде қайтіп жазады?
- Аралас санды бүтін және бөлшек бөліктерінің қосындысы түрінде жаз
2
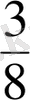 , 21
, 21
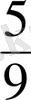 . 103
. 103
 .
.
- Қосындыны аралас сан түрінде жаз:
3+
, 13+
, 100+
, 7+
.
- Аралас сан түрінде жаз:
,
,
,
.
- Аралас санды бұрыс бөлшекке айналдыр
2
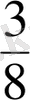 , 21
, 21
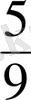 . 103
. 103
 .
.
1. 3. 4. Бөлшектерді ортақ бөлімге келтіру
Бөлiмдерi әр түрлi бөлшектердi салыстыру, қосу және азайту үшiн оларды бiрдей бөлiмге келтiру қажет. Бөлшектердi бiрдей бөлiмге келтiру үшiн олардың бөлiмдерiнiң ең кiшi ортақ еселiгi табылады.
Мысалы,
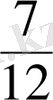 және
және
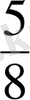 бөлшектерiн ең кiшi ортақ бөлiмге келтiрудi қарастырайық. Бұл бөлшектердiң бөлiмдерi 12 және 8 сандары. 12 және 8 сандарының ең кiшi ортақ еселiгi 24 саны. Онда 24 саны осы
бөлшектерiн ең кiшi ортақ бөлiмге келтiрудi қарастырайық. Бұл бөлшектердiң бөлiмдерi 12 және 8 сандары. 12 және 8 сандарының ең кiшi ортақ еселiгi 24 саны. Онда 24 саны осы
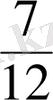 және
және
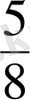 бөлшектерiнiң ең кiшi ортақ бөлiмi болады. Бөлшектердi бiрдей ең кiшi ортақ бөлiммен жазу үшiн бөлшектердiң әрқайсысының толықтауыш көбейткiштерiн табады: 24:12=2; 24:8=3. Ендi берiлген
бөлшектерiнiң ең кiшi ортақ бөлiмi болады. Бөлшектердi бiрдей ең кiшi ортақ бөлiммен жазу үшiн бөлшектердiң әрқайсысының толықтауыш көбейткiштерiн табады: 24:12=2; 24:8=3. Ендi берiлген
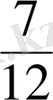 және
және
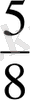 бөлшектерiн бiрдей бөлiммен (24) жазу үшiн, бөлшектердiң негiзгi қасиетiн пайдаланып, берiлген бөлшектiң алымын да, бөлiмiн де өзiнiң толықтауыш көбейткiшiне көбейтедi. Сонда
бөлшектерiн бiрдей бөлiммен (24) жазу үшiн, бөлшектердiң негiзгi қасиетiн пайдаланып, берiлген бөлшектiң алымын да, бөлiмiн де өзiнiң толықтауыш көбейткiшiне көбейтедi. Сонда
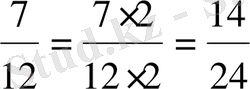 және
және
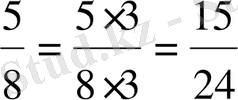 .
.
(
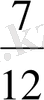 және
және
 ) = (
) = (
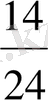 және
және
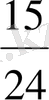 ) .
) .
Бөлшектер бiрдей бөлiммен жазылды.
Бұл тақырыпты оқып-үйренуден күтілітін нәтиже - бөлшектердің ортақ бөлімін таба алу.
Міндетті нәтижеге жеткен, жетпегенін анықтауға бағытталған сұрақтар мен жаттығулар:
- Мына сұрақтарға жауап бер:
- Бөлшектер ортақ бөлімге қалай келтіріледі?
- Бөлшектерді ортақ бөлімге келтіру бөлшектің қандай қасиетіне негізделген?
- Әрбір бөшек үшін қосымша көбейткіш қалай табылады?
- Бөлшектерді ортақ бөлімге келтіру дегенде нені түсінеміз?
- Бөлшектерді ортақ бөлімге келтір:
1)
және
; 2)
және
;
3)
және
; 4)
,
және
.
1. 3. 5 Бөлімдері әр түрлі бөлшектерді салыстыру
Бөлiмдерi әртүрлi бөлшектер бөлiмдерi бiрдей бөлшектер түрiне келтiру арқылы салыстырылады.
Мысалы,
 және
және
 бөлшектерiн салыстырайық.
бөлшектерiн салыстырайық.
Оқушыларға сұрақ: 1 алманың
 -i көп пе, әлде
-i көп пе, әлде
 -i көп пе? Сұраққа жауап iздеу үшiн, бөлшектердi бiрдей ең кiшi ортақ бөлiмге келтiредi.
-i көп пе? Сұраққа жауап iздеу үшiн, бөлшектердi бiрдей ең кiшi ортақ бөлiмге келтiредi.
 Сонда
Сонда
 пен
пен
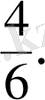 бөлшектерiн салыстырамыз. 3<4 болғандықтан
бөлшектерiн салыстырамыз. 3<4 болғандықтан
 <
<
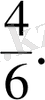 Демек,
Демек,
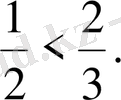
Сандық сәуледе
 пен
пен
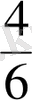 бөлшектерiне сәйкес нүктелердi тауып, салыстырғанда оқушылардың ойлары нақтыланады.
бөлшектерiне сәйкес нүктелердi тауып, салыстырғанда оқушылардың ойлары нақтыланады.
Аралас сандарды салыстыру үшiн алдымен бүтiн бөлiктерi салыстырылады, мысалы
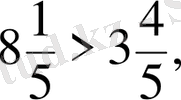 себебi 8>3, ал бүтiн бөлiктерi бiрдей болса‚ бөлшектiң үлкен-кiшiлiгi бөлшек бөлiгiне тәуелдi. Мысалы‚
себебi 8>3, ал бүтiн бөлiктерi бiрдей болса‚ бөлшектiң үлкен-кiшiлiгi бөлшек бөлiгiне тәуелдi. Мысалы‚
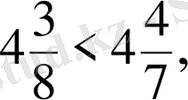 себебi
себебi
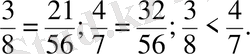
Бөлшектердi былай да салыстырады:
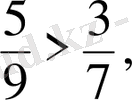 себебi
себебi
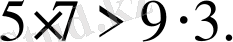
Бөлшектердi осы тәсiлмен салыстыра бiлу, бөлшектердi азайту тақырыбындағы азайғыш бөлшек азайтқыш бөлшектен үлкен, болу шартын анықтау үшiн қажет.
Оқыудың күтілетін нәтижесіне жеткендігін білу үшін оқушы мынадай сұрақтарға жауап беріп, жаттығулар мен есептер шығара алуы керек:
- Бөлімдері бірдей бөлшектердің қайсысы үлкен?
- Алымдары бірдей бөлшектер қалай салыстырылады?
- Бөлімдері әртүрлі бөлшектерді ортақ бөлімге келтіру арқылы слыстыру туралы айтып бер.
- Бөлімдері әр түрлі бөлшектерді ортақ бөлімге келтірмей қалай салыстыруға болады?
- Жұлдызшаның орнына < немесе > белгілерінің бірін қой:
- *; 2) *; 3) *.
- Өсу ретімен жаз:
,
,
,
,
,
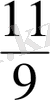
.
- Айсәуле кітаптыңбөлігін, ал Күнсұлу осы кітаптыңбөлігін оқыды. Олардың қайсысы көп оқыған?
- Сыныптан тыс уықытты оқушылардың-і спортпен шұғылыданады, -і басқа үйірмелерге қатысады. Қайсысы көп?
- Бірінші принтер 5 минутта 41 бет, екіншісі 3 минутта 28 бет басып шығарады. Қайсысының жұмыс өнімдулугі жоғары?
- Координаталық сәуледе,, ,, ,, , бөліктеріне сәйкес нүктелерді белгіле.
1. 3. 6 Жай бөлшектерді қосу және азайту
1. 3. 6. 1 Жай бөлшектерді қосу
Жай бөлшектердi қосу бөлiмдерi бiрдей бөлшектердi қосуды үйретуден басталады.
Тақтаға АВСD төртбұрышын салып, оны бiрдей 9 бөлiкке (үлеске) бөледi. Осы бiрдей бөлiктердiң 2 бөлiгiн бiр оқушыға‚ 5 бөлiгiн екiншi оқушыға боятып, сынып оқушыларынан барлығы неше бөлiгi боялғанын сұрасақ‚ оқушылар 7 бөлiгi боялғанын айтады. Бөлшек түрiнде жазғанда
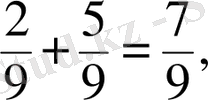 болады, әрiппен жазсақ:
болады, әрiппен жазсақ:
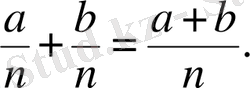
Осы есептеулерден соң, оқушылар бөлiмдерi бiрдей бөлшектердi қосудың ережесiн өздерi тұжырымдайды. Бөлімдері бірдей бөлшектерді қосу үшін, косынды бөшектің бөліміне бөлшектердің бөлімін, ал бөлшектердің алымдарын косып алым етіп жазады .
Оқушылармен мына типті бірнеше жаттығуларды ауызша орындау жеткілікті
- 37\frac{3}{7}+27\frac{2}{7}=3+27\frac{3 + 2}{7}=57\frac{5}{7};
- 16\frac{1}{6}+56\frac{5}{6}+26\frac{2}{6}=1+5+26\frac{1 + 5 + 2}{6}=86\frac{8}{6}=43\frac{4}{3}\= 113\frac{1}{3}.
Осы есептерді қарастыру барысында бөлімдері бірдей бөлшектекрдің қосындысы қысқаратын болса, қысқартып қою, егер бұрыс бөлшек болса, онда аралас бөлшек түрінде жазу керек екендігі айтылады.
Бұл сабақта бөлiмдерi әртүрлi бөлшектердi қосу тақырыбымен жалғастырылады.
Бөлiмдерi әртүрлi бөлшектердi қосу үшiн, оларды ең кiшi ортақ бөлiмге келтiрiп, сонан соң бөлiмдерi бiрдей бөлшектердi қосуды орындайды.
Мысалы,
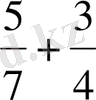 қосындысын табу үшiн, берiлген бөлшектердiң бөлiмдерiнiң ең кiшi ортақ еселiгiн табу керек. ЕКОЕ (7, 4) =28. Демек,
қосындысын табу үшiн, берiлген бөлшектердiң бөлiмдерiнiң ең кiшi ортақ еселiгiн табу керек. ЕКОЕ (7, 4) =28. Демек,
 және
және
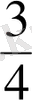 бөлшектерiнiң ең кiшi ортақ бөлiмi 28-ге тең болады. Бiрiншi қосылғыштың толықтауыш көбейткiшi 28:7=4, ал екiншiсiнiкi 28:4=7.
бөлшектерiнiң ең кiшi ортақ бөлiмi 28-ге тең болады. Бiрiншi қосылғыштың толықтауыш көбейткiшi 28:7=4, ал екiншiсiнiкi 28:4=7.
Бөлшектердi бiрдей ең кiшi ортақ бөлiмге келтiрiп жазатын болсақ:
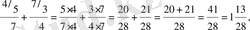
қысқаша
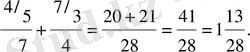
Бөлімдері әр түрлі бөлшектерді ортақ бөлімге келтіру үшін, бөлшектің бөлімдерінің ЕКОЕ табу арқылы бірнеше есеп шығарғанан кейін, қандай жағдайларда ортақ бөлімді бірден табуға болатын жағдайларын да ескерту керек:
1) егер бөлшектердің бөлімдері өзара жай сандар болса, онда ортақ бөлім олардың көбейтіндісі болады;
2) егер екі бөлшектің біреуінің бөлімі екінші бөлшектің бөліміне еселі болса, онда еселі сан бөлшектің ортақ бөлімі болады;
3) басқа жағдайларда бөлшектің бөлімдерінің ЕКОЕ табылады.
Осындай үш жағдайға да оқушылар жаттығуы керек.
Бөлшектердi қосудың ауыстырымдылық және терiмдiлiк қасиеттерi орындалатынын оқушылардың өздерi есептетіп, көз жеткiзiледi.
Жай бөшектерді қосу тақырыбын оқып-үйренуден күтілетін нәтижелер.
- Мына сұрақтарға жауап бере білу:
- Бөлімдері бірдей бөлшектер қалай қосылады?
- Бөлімдері бірдей бөлшектер қосу ережесін әріптермен жазу.
- Бөлімдері әр түрлі бөлшектерді қосу қалай орындалады?
- Егер бөлшектердің бөлімдері өзара жай сандар болса, онда ортақ бөлім неге тең?
- Егер екі бөлшектің біреуінің бөлімі екінші бөлшектің бөліміне еселі болса, онда бөлшектің ортақ бөлімі неге тең?
- Төмендегідей бөлшектерді қоса алу:
- 835\frac{8}{35}+735\frac{7}{35}; 2) 59\frac{5}{9}+78\frac{7}{8}; 3) 1621\frac{16}{21}+57\frac{5}{7}; 4) 142\frac{1}{42}+263\frac{2}{63}.
Бөлшектердi қосуда қосудың ауыстырымдылық және терiмдiлiк қасиеттерi орындалатынын оқушылардың өздерiне есептетiп, көз жеткiзiледi.
Аралас сандардың бүтiн бөлiктерi натурал сандар болғандықтан, аралас сандарды қосу натурал сандарды қосу мен бөлiмдерi әр түрлi бөлшектердi қосудан құралады.
Сонымен қатар аралас сандардың бүтiн бөлiктерiн бөлек, бөлшек бөлiктерiн бөлек қосу үшiн, қосудың ауыстырымдылық және терiмдiлiк қасиеттерi пайдаланылады. Мысалы,
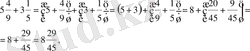
қысқаша
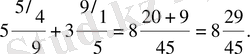
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz