Математика тарихы және методология пәні

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 14 бет
Таңдаулыға:

6. Лекциялық кешен (лекция тезисі)

№1 лекция тақырыбы. Математика тарихы және методология пәні. Математика мұғалімін дайындау жүйесіндегі математика тарихының және методологиясының ролі.
Математиканы терең игеру оның тарихын, оның негізгі идеяларын және оның дамуын оқып білмеу мүмкін емес. Математиканың бүтіндей дамуының тарихын білуге деген құштарлықсыз әсте мүмкін емес. Математика тарихы мәселелерімен осы саладағы мамандар ғана емес, сонымен қатар әртүрлі математикалық пәндердің өкілдері де жүйелі айналысып жүргенін атап өткен жөн.
Математика тарихын кезеңдерге бөлу мәселесіне тоқталайық. Математика тарихын өзіне тән ерекшеліктері бар бірнеше кезеңдерге (периодтарға) бөлуге болады.
Математика тарихының бірінші кезеңі ғылымға дейінгі кезең. Математика өте ежелгі ғылым. Адамдар сандар мен оларға амалдар қолдануды ертеден білген. Төрт және одан да көп мыңдаған жылдар бұрын келе жатқан арнайы математикалық тексттер бар. Олар қазір дәлелденген. және мектептерде жаттығу материалы ретінде қолданылады. Бұл кезеңде өте маңызды математикалық ұғымдар мен амалдар пайда бола бастаған.
Бұрыш, аудан, көлем тағы сол сияқты көптеген абстрактлі ұғымдар пайда бола бастады. Егер де біз аудан, көлем, тағы сол сияқты ұғымдардың мағынасымен, мәнімен танысқымыз келетін болса, математика тарихының осы бірінші кезеңіне жүгінеміз. Бұл кезеңде көптеген есептерді шешу алгоритмдері пайда болғанымен, олар тек қана мысал ретінде қарастырылды. Бұл кезеңде алғашқы қауымдық құрылыс халықтарының және ежелгі египеттіктер мен вавилондықтардың математикасын жатқызады. Бұл кезеңдегі математиканың мазмұнымен таныса келе, көптеген маңызды және қиын тарихи математикалық сұрақтар өте ежелгі уақытта пайда болғанын көреміз.
Екінші кезеңге антикалық грек математикасының тарихы жатады. Бұл кезеңде математика өзіне тән және қазіргі кезеңге дейінгі сақталған ерекшеліктері бар ғылым болды. Нақты сандарға бөліну теориясында, интегралдық және дифференциалдық есептеулерге, алгебраға, аналитикалық геометрияға тағы сол сияқты математиканың басқа да салаларына байланысты есептер шығарылды. Бұл есептермен қазіргі математика тарихшылары жұмыс жүргізіп жатыр.
Математика тарихындағы үшінші үлкен кезең ол элементар математика кезеңі. Бұл кезеңде ежелгі және орта ғасырлық Үндістан мен Қытайдың, орта Азия мен Кавказдықтардың, Арабтар мен орта ғасырлық европалықтардың қайта өрлеу дәуіріндегі халықтардың математикасын жатқызуға болады. Сонымен қатар үшінші кезеңде астрономияға қажетті есепте алгоритмі мен тригонометриялық функциялар және олармен байланысты кубтық теңдеулерді шешу алгоритмі табылды. Тағы сол сияқты бұл кезеңге ХІ-ХVІ ғасырлардағы орыс математиктерінің қолжазбаларын жатқызуға болады.
Математика тарихының төртінші кезеңіне ХVІ-ХVІІІ ғасырлардағы европалықтар математикасын және Петербург ғылым академиясының қызметін жатқызамыз. Бұл кезең әріптік есептеулердің және математикалық анализдің пайда болуымен, сонымен қатар айнымалы шама ұғымымен, жалпы функция ұғымының пайда болуымен сабақтасады. Диалектикалық материалдың негіздемелерімен айналыса жүріп, К.Маркс өзінің материалистік қолжазбаларында осы кезеңнің дифференциалдық есептеулеріне байланысты арнайы очерктер жазған.
Соңғы бесінші кезеңге ХІХ-ХХІ ғасырдың математикасын жатқызды. ХІХ ғасырлардағы математика тарихы туралы мағлұматтарды Кеплер, Ковалевская, Декарт, Ферма, Ньютон, Лейбниц, Бернулли, Эйлер, Лагранж және т.б. еңбектерінен кездестіруге болады.
Математиканың тарихын кезеңдерге бөлу оның басты идеяларымен әдістеріне және өзіне тән ерекшеліктеріне байланысты. Бұл кезеңдер жалпы тарихи кезеңдермен сәйкес келеді. Шынында да, бастапқы кезде біз алғашқы қауымның және құлиеленушілік қоғамының адамдарының математикалық білімдерімен жұмыс жасасақ, одан кейін ежелгі гректердін математикасына көштік. Яғни, құлиеленушілік қоғамының дамыған математикасымен жұмыс жасай бастадық. Ал үшінші кезең негізінен өндірістің феодалдық қоғамды, төртінші капитализмнің қалыптасу кезеңіне, ал бесінші кезең - бұл капитализмнің қалыптасқан кезеңімен және қазіргі кезеңді қамтиды.
Жастарды тәрбиелеумен оларға математиканы үйрету мақсатында математика тарихының маңызды роль атқаратынын атап өту жөн. Оқушылармен математиканың тарихы туралы әңгіме олардың ой өрісін жетілдіріп, сол пәнге деген қызығушылығын арттыратынын мұғалімдер біледі. Ғалымдардың шығармашылық өмірінен мысал, олардың ашқан жаңалықтары, оқушылардың өз-өзіне деген сенімін арттырады және қазіргі ғылымның мәселелерін шешуге деген ынтасын арттырады. Тарихи әңгімелер оқушыларды қазіргі ғылымның негізгі оның тарихынан басталатын және болашағы зор екенін көрсетеді. Сондықтан мектеп, жоғары оқу орындары мұғалімдерінің және оқушылар мен студенттердің математика тарихына деген қызығушылығы мен ынтасы уақытша болу мүмкін емес. Әрбір сабақта оқушылардың жас ерекшеліктеріне байланысты 3 немесе 5 минутқа арналған тарихи мәліметтер келтіріп отыру керек. Әр кластарда тарихи тізбектелуді сақтаймын деп әңгімелесу және қайталау міндетті түрде емес. Бұл әңгімелер мазмұны бойынша бірдей болып, бірақ алып отырған аумағы мен түп мағынасы әртүрлі болып кетуі мүмкін.

Әдебиеттер: [2,4-6]; [14,15,17];[26-31];[32-34]; 35-37].

№2 лекция тақырыбы. Алғашқы математикалық түсініктер мен көріністердің қалыптасуы (сан, геометриялық фигуралар туралы түсініктер).
1. Карл Гаусс математиканың сан салаларын сарапқа сала келіп, арифметиканы математика патшасы деп бағалаған. Ал арифметиканың негізгі ұғымы- сан. Ендеше, сол сан ұғымының қалай пайда болганын ашу, білу - ғылыми методологиялық үлкен проблема.
Сан туралы ұғым адамзат мәдениетінің тууымен және оның дамуымен тығыз байланысты. Шынында, егер осы ұғым болмаса, өзіміздің рухани өміріміз бен практикалық қызметімізді тиісті дәрежесінде көрсете алмас едік. Есеп-қисап жүргізу, уақыт пен қашықтықты өлшеу, еңбек нәтижелерінің қорытындыларын есептеп шығару сан ұғымынсыз мүмкін емес. Сан - математика ғылымының іргетасы.
Карл Маркс "А.Вагнердің кітабына ескертпелер" деген еңбегінде: адамның табиғатқа қатынасы әуел бастан теориялық жолмен емес, практикалық, яғни әрекетке негізделген жолмен басталады, - деп жазған. "Әрбір жануар сияқты, олар да (алғашқы қоғам адамдары да. - О.Ж) ішіп жеуден бастайды, т.б., яғни, қандай болса да бір қатынаста "қалып қоймай", белсенді әрекет арқылы сыртқы дүниенің белгілі бұйымдарын меңгеруден, сөйтіп өздерінің мұқтаждықтарын қанағаттандырудан бастайды".
Сан немесе геометриялық фигуралардың математикалық ұғымы, математикалық текстерден едәуір ерте пайда болған. Бізге оңай болып көрінген сан және геометриялық фигуралар ұғымы негізінде абстрактілі ұғымдар болған. Бірақ өте ұзақ және тиянақты ойлау жұмыстарын кейін бұл ұғымдар қалыптасты.
2 және 5 сандарының жалпы ұғымынан бұрын 2 қол және 5 саусақ ұғымы пайда болған. Алғашқы қауымдық құрылыс аңшылары өздерінің иттерінің түгел екенін санап білген жоқ, жай ғана көзінің ұшқырлығымен қай иттің жоқ екенін анықтай алған. Мұндай сезімдік есеп сонымен қатар өзінің балапандарының санын біле алмайтын үйрекке де тән қасиет және бұл негізгі санақтан бұрын пайда болған. Негізгі санақтың пайда болуындағы алғашқы қадамның бірі: саналатын заттар мен берілген заттар жиынындағы өзара бірмәнділік, сәйкестік.
Салыстыратын заттардың жиыны алдын ала белгісіз болуы мүмкін. Алмастыру кезінде алғашқы қауымдық құрылыс адамдары ауыстырылатын заттарды екі қатарға қойып, өзара бірмәнділікке келтірген. Содан кейін қолдың 5 саусағы сияқты немесе басқа да арнаулы таяқшалар мен тастар секілді санақ эталондары пайда бола бастады. Нақты бір санды анықтайтын эталондар жиынының пайда болуы сан ұғымының пайда болуына әкелді. Мұндай эталондар табиғи болды, яғни адам айдың біреу екендігін, адамда 2 қол, 2 аяқ, 5 саусақ бар екенін білетін. Сондықтан 1, 2, 5 сандарын осындай салыстырулармен көрсету таңқаларлық жайт емес. Санақ үшін өте тиімді эталондар қолдың саусақтары болды. Сондықтан болар, абипондар тайпаларында 5 деген - бір қол, 10 деген - 2 қол, 20 деген - қол және аяқ деген ұғымдар пайдаланылды.
Қазір Европа мен Азия да сан ұғымының қай уақытта пайда болғанын зерттеп жатыр. Тілдері ұқсас халықтардың кейбір сандарды атауында ұқсастықтардың болатынын көруге болады. Мысалға: орыстың один, немістің ЕІНС, ағылшынның Уан, француздың Ун, латынның унус. үнді Европа халықтарының сандарының аталуының ұқсастығынан, сандардың аталуы ерте уақытта пайда болғанын және олар бір тілде сөйлегенін көре аламыз. Сонымен қатар ертедегі француздар, грузиндер 10-дық санақ системасымен емес 20-лық санақ системасымен санаған. Мысалы: грузиндер - 10 - ати, 20 - оци, 30 - оцдаати (20+10), 40 - ормоци (20·2), 50 - ормоцдаати (20·2 +10) тағы сол сияқты.
2. Нақты геометриялық фигуралармен адам еңбек еткенде, еңбек құралдарын жасауда, жерді өңдегенде және үй ғимараттарын салғанда кездескен. Өте ерте кезде дөңгелек, төртбұрыш, үшбұрыш, ромб, сегмент формаларында пышақтар мен найзалар жасала бастаған; әдетте жерді төртбұрыш формасы ретінде жыртқан, ал үй ғимараттары конус, цилиндр, параллелипипед, пирамида формасында салынған. Қазіргі геометрияда фигуралардың атаулары грек тілінде. Мысалға, центр - centrum (грекше) деген сөзінен, бұл: ұшы үшкірленген өгіз айдайтын таяқ, - деген ұғымды көрсетеді (алғашында бұл сөз дөңгелек сызатын циркульдің ұшы деген мағынаны берген).
Ромб - грекше зырылдауық, трапеция - стол деген сөздерден пайда болған. Ал призма - арамен кесілген, конус - бүршік, сфера - доп деген, цилиндр - каток, пирамида - пурама деген сөздерден шыққан. Ал сызық - деген сөз латынша зығыр деген сөз, нүкте - шұқу, түрту деген сөзден шыққан. Бұл мысалдар алғашқыда геометрияда геометриялық эталондардың болғанын дәлелдейді.
Сан ұғымының қалыптасу процессі
1. Адамдардың сан ұғымы жайлы түсінігі туа пайда болған жоқ. Олар шынайы заттардың қасиеттерінің және арақатынастарының көрінісі болып табылады. Олар адамдардың белсенді қызметтері кезінде қолданылады. Адам миының ұзақ мерзімді эволюциясынан кейін есептеуге және өлшеуге қажетті абстракциялар құруға қабілеті жетті.
2. Бастапқыда сезімдік санақ болды, яғни берілген жиын басқа көп санды (көп мағыналы) жиынмен салыстырылды. Сандық мөлшерлік қасиеттердің нақты жиын қасиеттерінің жиынтығынан бөліну процессі, оның функционалдық ролінің мойындалуы, ұзақ тарихи кезеңді қамтиды.
3. Адамдардың интеллектуалды дамудың жоғарғы деңгейіне ауысуы сезімдік санақтың кемшіліктерін көрсетті. Жиындардың бір санды еместігі, артық, кем - деген ұғымға әкелді.
4. Саусақтар мен бақайлар, тастар сияқты санақ эталондары жиындардың сандық тұрғыдан қаралуынша әкеліп соқты.
5. Сандардың атаулары енгізілді, сан туралы жалпы ұғымдар қалыптаса бастады (натурал сандар).
6. Натурал сандар шамасы бойынша салыстырылды. Алғашында қысқа-қысқа натурал сандар тізбегі бойынша, ал кейінен тізбек ұзартылды.
7. Жазулар пайда бола бастады. Символикалық аппарат дамыды.
8. 5+, 10+, 12, 60-тық санақ жүйелері пайда болды. Барлық тарихшылар оң нақты сан ұғымының пайда болу кезеңін осылай қарастырады. Сандардың жалпы кластар туралы ұғымы кейіннен қалыптасты. Дәл осы сияқты геометриялық фигуралардың пайда болу кезеңін бөлуге болады.

Әдебиеттер: [2,4-7,11];[14,15,17]; [26-31]; [32-34]; [35-37].

№3 лекция тақырыбы. Ежелгі Египет және Вавилон математикасы.
1. Ежелгі математикалық жазбалар бүгінгі күні Ніл даласындағы ежелгі Шығыс цивилизациялары Египет пен Вавилонда пайда болғаны белгілі болып отыр. Ежелгі Египет пен Вавилонмен бір кезеңде Индияда, Қытайда, Орта Азия мен Закавказияда, Үндіқытай мен Индонезияда, Жерорта теңізінің Европалық және азиялық жағалауындағы аралдарда цивилизация пайда болды. Математикалық құжаттар тек Египетте, Мессопотамияда, Индия және Қытайда ғана сақталған. Осы мемлекеттердің барлығы егін шаруашылығымен айналысты. Егін шаруашылығына жарамды аудандар аз болғандықтан оларды каналдар салу және батпақты жерді құрғату жұмыстары селолық қауым құруды талап етті. Бұл қауымдардың натуралдық шаруашылығымен қатар маңызды қоғамдық жұмыстармен, сонымен бірге меншікті әскери бөлімдерге байланысты бөлінулер пайда болды.
Бұл мемлекеттерде қаналдар салғанда, плотина, астық қоймаларын, храм және әскери бекіністер құрылыстарында, материалдарды бөлу және әскери жорықтарға және қоғамдық жұмыстарға қатысушылар арасында тамақ бөлу негізінде есептеулер пайда болған, қажеттіліктен туған есептеулер. Математикалық есептер пайда болуына әкеп соқты. Біз бұл есептерді әртүрде бүгінгі күнге дейін сақталған математикалық құжаттардан білеміз. Египетте математикалық жазбалар нәзік папируста, кейде былғарыда жазылған және де солардың ішіндегі, марқұмның жақсы көретін шығармасын, о дүниеде оқысын деген оймен жоғарғы қызметтегі египеттіктердің қабыр-пирамидаларына қойылған жазбалар ғана сақталған. Ал Вавилондық жазбалар сына жазумен өңделмеген саз балшыққа жазылып, онан соң күйдірілген және де бүгінгі күнге қисапсыз, орасан мол математикалық сына жазбалары жетті. Вавилон жазбаларымен салыстырғанда нашар (аз) мәліметіміз бар. Ежелгі Египеттің математикасын қарастырайық.
Ежелгі Египеттің ескерткіштерінде сақталған математикалық жазбалардың көбісі папирус қағазда жазылған. Бүгінгі күнге дейін сақталған ең үлкен ежелгі египеттік жазба ол 5,25 м :: 33 см өлшемді 84 есептен тұратын Райнд папирусы. Папирус иесінің атымен аталған, ол папирусқа 1858 жылы ие болған. Қазіргі кезде папирус Британияның Лондондық музейінде және Нью-Йоркте сақталады. Ал екінші папирусқа (5,44 см :: 8 см) өткен ғасырдың аяғында шығыстанушысы орыс В.С. Голенищев ие болған. Бүгінгі күні ол Пушкин атындағы бейнелеу өнер музейінде сақталады. Бұл папирус орамы 25 есептен тұрады. Екі папирустағы жазбалар да қазіргі заман тіліне аударылған және түсінік берілген, олар орта патшалық дәуіріне жатады. Алған білімін таратушылар мемлекеттік және меншіктік қызметте тұрған чиновниктер болды. Біз жаңа патшамен ежелгі патша дәуірлеріндегі математикалық мағұлматтар жайында ешқандай хабардар емеспіз. Шынына келсек кейбір үзінділерге қарағанда және Москвалық папирус пен Райнд папирусы құрастырылғаннан бері математика азақ өзгерді.
Египеттің мұнан әрі даму тарихы ол біздің эрамызға дейінгі бірінші мыңжылдық тарихы, яғни мемлекеттің құлауы мен шетел жаулап алушыларының үстемдігі алғашқыда эфиоптар, одан кейін ассириялық пен перстердікі. Египетті Александр Македонский жаулап алғаннан кейін грек және египет мәдениетінің жемісті синтез дамуы басталды. Александрия эллинизм дәуірінің туу шағында ғылым орталығы болып қалыптасты және ол бұл мағынасын, Римнің Египетті жаулап алғаннан кейін көптеген ғасырлар бойы сақтан отырды.
Тағы да Египеттіктердің математикалық жұмыстарымен эллинизм дәуірінде және ислам дінінің өрістеу кезеңінде кездесеміз, бірақ бұл мүлде басқа мәдениет пен математика. Ежелгі Египеттік өркениет өзінің кезеңін аяқтады.
Египеттіктердің геометриялық білімдері аудан мен көлемдерді есептеуге қатысты. Бұлардан табылған кейбір нәтижелер тамаша болды, бірақта геометриялық математикасы жеке салаға бөлінген жоқ.
Дөңгелектің ауданы диаметрдің бөлігінің квадратына тең деген жақсы жуықтауды қолданады .
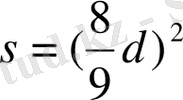Бұл ереженің табу әдісі белгісіз, А.Е. Райктің шаршы торының жүйелі жағдайы туралы гипотезасы шындыққа негізделген. Диаметрі d-ға тең дөңгелектің ауданы қабырғалары 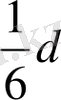, 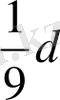тең кішкене шаршылар алынып тасталынған сырттай сызылған шаршының ауданымен салыстырылады.
Ежелгі Египетте математика әлі арифметика, алгебра, геометрия және алгебралық, геометриялық және бөлшектерге қосымша сандық шешулер үшін ережелер жиынтығы ретінде бөлінбеген білімдердің жүйесі болып табылады. Египеттік кеңес хатшыларының алдындағы негізгі мәселе ол практикалық болды. Осымен қатар есептер жалпыланып абстрактлық сипаттама қабылдай бастады. Жеке мәселелерді зерттегенде математикалық дедукцияның бөліктерінің өсу қарқынын білдіретін геометриялық, алгебралық және арифметикалық әдістер туады.
Ежелгі Египет математикасы ғылымның дамуына сөзсіз ықпал жасады.
Вавилон математикасын оқып білудің негізгі деректері археологиялық қазбалардың арқасында табылған математикалық сына жазулар. Сына жазулардың мағынасын түсіндіріп, талдау жасап, ашқан ежелгі Қосөзен. Көп үлес қосқан адам О. Нейгебауер.
Египеттегі сияқты бұл елде де, қоғамдық жұмыстарды, шаруашылықты санауды, қорытынды қағаздарды дайындауды жазушылар атқарған.
Математикалық сына жазулардың оқу сипаты бар және негізінен есеп айыратын тапсырмалары бар. Есептердің арасында кеңейген алгебралық есептер класымен бейнеленетін сызықты теңдеулер жүйесі және екінші дәрежелі теңдеулер кездеседі.
Вавилондықтардың геометриялық білімінің көп бөлігі, египеттіктердікі сияқты үй салуда, құрылыста кездесетін жай фигураларды өлшеу болып табылады. Бірақ, алгебрадағыдай вавилондықтар геометрияның жалпы және жеке жұмыстары бойынша алда. Бұның дәлелі ретінде олардың құрастырған есептері және жалпы ережелердің түрін, теоремалар және анықтамаларды құрастырады жою сирек кездеседі. Египеттіктерден айырмашылығы кейбір дұрыс көпбұрыштар, дөңгелектің сегменті және қиық конус оқытылды.
Вавилонда ашылған керемет жаңалықтың бірі, сына жазуларда бірінші пайда болған және жалпы жағдайлар үшін Пифагор теоремасы.
Вавилондықтар тікбұрышты үшбұрыштың қабырғаларының арасындағы сандық қатынастарды білген.
Вавилондықтардың Пифагор теоремасына қалай жеткені белгісіз.
Квадраттық теңдеуге берілген бір есепті қарастырамыз. Бұнда маңызды ролді теорема атқарады.
Есеп. Алдымен қабырғаға тігінен тұрғызылған таяқшаның (х) ұзындығын табу керек, одан кейін жоғарғы басы 3 шынтаққа төмен түсіп тұратын, төменгі жағы қабырғадан 9 шынтаққа төмен тұратын аралас болып келетін таяқшаның ұзындығын табу керек. 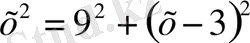теңдеуі бізге 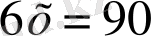, 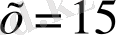өрнегін береді. Кейін бұл материал ежелгі Қытай және Үнді математикасында болады.
Пифагор теоремасын вавилондық ғалымдар дұрыс көпбұрыштарды қарастырған кезде қолданған.
Дұрыс көпбұрыштардың қатаң теориясы Пифагор мектебінің жетістіктерінің бірі.
Есептеудің жаңа әдістері құрастырылған, жаңа бүтін бағыттар пайда болды, логикалық дедукция элементтерінің өсуі байқалады. Сол кезде ежелгі Вавилон математикасында көптеген ережелердің арасындағы ішкі логикалық байланыс әлі әлсіз болды және жекелеген қорытындылар бірігіп, бір жүйеге айналмады. Математикалық ойлауға, тереңірек талдауға ұмтылу тән болмады, ең алдымен талап етілген зат - бұл нақты көрсету болатын, ал ғалымдар ережелердің дұрыстығына ешкімнің көзін жеткізгілері келмеді.
Соған қарамастан бұнда бірінші рет есептеу жүйесі шықты, бірінші болып сызықты және квадрат теңдеулер алгебрасы шықты және де жоғарғы дәрежелі жай теңдеулер қарастырылған. Пифагор теоремасы ашылды, геометриядан дұрыс көпбұрыштар туралы білім ашылды, сандар теориясының бірінші есептері шығарылды, оларды диофантты талдауға жатқызады. Ежелгі Вавилон математикасының жетістіктері күмән тудырмауы керек. Вавилон математикасы кейінгі математиканың дамуына зор үлес қосты.
Вавилондық алпыстық нөмірлеу Грецияның бөлшектер арифметикасына және дөңгелекті бөлуге әсер етті. Оны қазір де қолдануда. Вавилондық алгебраға алдымен Герон, кейін Диофант, одан кейінірек әл-Хорезми және ислам елдерінің алгебралық мектептерінің негізін салған т. б. адамдар таң қалған.
Египеттік және Вавилондық мемлекеттер тарихи сахнада бас иген кезде жаңа халық пайда болған. Олар - гректер. Гректер Шығыс елінің ғалымдарына міндетті болған. Бірақ көп ұзамай Гректер олардан асып түсіп, бірінші рет математиканы нақты ғылым етіп дамытты.
Әдебиеттер: [2,4-6,8-10]; [14,15,20];[26-31]; [32-34];[35-37].

№4 лекция тақырыбы. Ежелгі және Орта ғасырлардағы Қытай математикасы (Қайнар көздер. Номерлеу. Тоғыз кітаптағы математика. Сызықтық теңдеулер жүйесі. Теріс сандар. Квадрат теңдеулер. Геометриялық, теориялық-сандық есептер).
Қайнар көз. Қытай цивилизациясы біздің эрамызға дейінгі (б.э.д.) ІІ ғасырдың басында Хуанхэ өзенінің жағалауында басталды. Олар жазба ескерткіштерде (біздің эрамызға дейін XVIII-XII ғғ.) - жануарлардың сәйектеріне жазылған жазулар да кездесті. Б.э.д. XIV ғасырда Хэнаниде табылған сәйектерде цифрлардың белгілеуі сақталған. Б.э.д. XIІІ-ХІІ ғғ. ыдыс сынықтары геометриялық орнаменттермен, мысалы, бес бұрыш, жеті бұрыш, сегіз бұрыш және тоғыз бұрыш бейнелерімен өрнектелген.
Б.э.д. ХІІ ғ. - добродетельное поведение әйренуінің негізін және Қытайда математика мен астрономияның пайда болуын зерттеуші атақты философ Конфуцияның қызметі.
Бөлшектер.
Қытайлықтарда бөлшектер теріс сандардан бұрын бүтін сандармен қатар пайда болды. Ең алғашқы бөлшектер 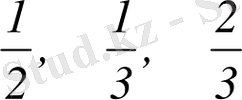болды, олар сәйкесінше жартысы, кіші жартысы, үлкен жартысы деген атпен өмірде де, математикалық текстерде де қолданылады. Бөлшектерді көбейту мен бөлудің жалпы ережесінің қазіргі ережеден аз ғана өзгешелігі болды. Онда ең кіші ортақ еселіктің орнына олардың көбейтіндісі алынды. Бұл есептерде бөлшектерді бөлу қазіргідей емес, бөлшектерді ортақ бөлімге келтіру арқылы орындалады
.
Тек қана V ғасырда ғана бөлшекке бөлу алымы мен бөлімі аударылып жазылған көбейтіндімен ауыстырылады. бөлшегі алғашқы ережесі бойынша m:n бөліндісінің нәтижесі сияқты емес, m бүтін санының алдыңғыдан n есе кіші саны ретінде қарастырылады.
Тоғыз кітаптан тұратын математика. Бұл кітап (б.э.д. ІІғ.) жер өлшеушілерге, инженерлерге, чиновниктерге және саудагерлерге арналған. Ол 246 есептен тұрады.
Бірнеше белгісізі бар сызықтық теңдеулер системасы. Фан-чэн әдісі сызықтық есептерді шешудегі қытай математиктерінің жетістіктерінің шыңы болып табылады. n белгісізі бар n сызықтық теңдеулер системасын шешу алгоритмі негізінен Гаусс әдісіне сәйкес келеді. Мұндағы барлық амалдар есептегіш тақтада орындалады. Қазіргі жағдайда бағаналары теңдеулер болатын, ал жолдары белгісіздер коэффициенттері және бос мүшелер болатын матрица қолданылады деп айтуға болады. Фан-чэн сөзі сандарды торға (клетка) орналастыру дегенді білдіреді.
Теріс сандар. Теңдеулер жүйесіне фан-чэн әдісін қолданудың қажетті шарты теріс сандарды енгізу болды. Мысалы,
жүйесін шешуде
кестесін алдық.
Келесі қадам: оң жақтағы 3-бағананың элементтерін біріншінің элементтерінен алу теріс санның пайда болуына алып келеді
Квадрат теңдеулер.
Көп жағдайларда қытайлықтар жүйелерді сызықтық теңдеулерге келтіреді.
жүйесі оған эквивалент теңдеуімен ауыстырылады.
Геометриялық есептер. Тоғыз кітаптан тұратын математиканың ІХ-ші кітабы шешуде Пифагор теоремасы қолданылатын геометриялық есептерге арналған. Осыдан Пифагор теоремасы б.э.д. VI бұрын белгілі болған деген жорамал бар. Бұл теореманың дәлелдеуі сызбаға негізделген. Тікбұрышты үшбұрыштың а, в катеттерінің қосындысы арқылы салынған квадрат осы катеттердің айырмасы арқылы салынған квадрат пен қабырғалары а, в болатын 4 тік төртбұрыштың қосындысы түрінде және гипотенуза бойынша салынған квадрат пен берілген үшбұрышқа тең 4 үшбұрыштың қосындысы түрінде көрсетіледі, яғни осыдан қатынасы шығады.

Ежелгі және Орта ғасырдағы Қытай математикасының мәні. Қытай математикасы XIV ғасырға дейін дамыды. Ол есептегіш тақтада арифметикалық, алгебралық, геометриялық кейбір есептер классын шешуге арналды. Қытай математиктерінің басты нәтижесі теріс сандарды енгізу болды, оған олар қарапайым түсіндірме берді. ХІІІ-ХV ғғ. Қытай, Үндістан, Орта Азия, Ислам елдерінің арасында мәдени алмасу болды.
Қытай математикасы, Үндістан және Ислам елдері арқылы Европа математикасына әсер етті, бірақ Қытай математиктерінің көптеген басты ашылулары Европада кеш белгілі болды.
Әдебиеттер: [2,4-6,8-10]; [14,15,20]; [26-31];[32-34]; [35-37].

№5 лекция тақырыбы. Ежелгі және Орта ғасырлардағы Үнді математикасы (Қайнар көздер. Позициялық ондық номерлеу. Сандарға қолданылатын амалдар. Алгебралық символика. Теріс және иррационал сандар. Геометриялық білімдер. Тригонометрия. Сандық қатарлар. Комбинаторика)
Б.э.д. ІІІ мыңжылдықта алғашқы халқы қоныстана бастаған үнді жерінде өркениеттің дамуы басталды.
Б.э.д. VІІ-V ғасырларға үнді жеріндегі алғашқы математикалық ескерткіштер кіреді.
Б.э.д. І мыңжылдықта брахмандардың Веды (білім) атты кітаптары пайда болды.
VІІ-VІІІ ғасырларда Ариабхата мен Брахмагупта еңбектері бүкіл ислам еліне танымал болды және араб тіліне аударылды.
Б.э.д. ІХ ғасырдан кешікпей үндіде Вавилон халқымен байланыс орнады. Оңтүстік үндіде Магавира (ІХ ғ.), Бхаскара (ХІІ ғ.) математиктері еңбек ете бастады.
Үнділіктердің ғылыми трактаттарының көбі - санскритте жазылған. Яғни, брахмандардың діни кітаптарының тілінде. Тек қана ХVІІ ғасырда Үнділіктер ғылыми трактаттарды қатынас тілінде жаза бастады.
Осы жерде ежелгі және орта үнді математиктері туралы мәліметтер толық емес екендігін атап өту керек.
Астроном-математиктердің еңбектерінің ең маңыздысы 628 жыл шамасында Брахмагупта жазған Сидханта, яғни оқу еңбектері болып табылады. Ол 20 кітаптан құралатын Усовершенствованное учение Брахмы деп аталады және 1 бөлімі астрономдарға арналған, ал ХІІ кітап арифметика мен геометрияға, ХVIII кітап алгебраға негізделген.
ХІІ ғасырда өмір сүрген ірі үнді математигі Бхаскараға Венец учения деген трактат жазды және бұл трактаттың алғашқы бөлімі арифметикаға, екіншісі алгебраға, соңғы 2 бөлімі астрономдарға арналған 4 бөлімнен тұрады.
Арифметикалық амалдар. Үнділер алғаш рет нөмірленген сандарға негізделген арифметикалық амалдардың ережесін жасап шығарды. үнділер арифметикалық амалдарға: қосу, азайту, көбейту, бөлу, квадрат және кубқа шығару, квадраттық және кубтық түбірлерден ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.