Жиындар теориясының негіздері: жиындар, операциялар, қатынастар және функциялар


1 Жиындар теориясының негізгі ұғымдары
1. 1 Жиындар
Жиын математикадағы негізгі ұғымдарының бірі болғандықтан, оған анықтама берілмейді. Жиын деп белгілі математикалық объектілердің жиынтығын түсінеміз. Ол объектілер жиынның элементтері деп аталып, кіші әріптермен, ал жиынның өзі бас әріппен белгіленеді.
а элементі А жиынына тиістілігін а
 А, “
А, “
 ” - тиістілік кванторымен белгілейді.
” - тиістілік кванторымен белгілейді.
b
 A - b элементі А жиынына тиісті емес.
A - b элементі А жиынына тиісті емес.
Бізге белгілі жиындарды атап өтейік:
N - натурал сандар жиыны;
Z - бүтін сандар жиыны;
Q - рационал сандар жиыны;
R - нақты сандар жиыны;
C - комплекс сандар жиыны;

Ø - бос жиын.
Жиі қолданылатын кванторлар:
 - кез келген,
- кез келген,
 х
х
 А (кез келген х А жиынында жатады) ;
А (кез келген х А жиынында жатады) ;
 - табылады,
- табылады,
 у
у
 В (В жиынынан у элементі табылады) ;
В (В жиынынан у элементі табылады) ;
׃ ( ) - мынадай, қасиетін сипаттау үшін;
 - бұдан шығатын салдар;
- бұдан шығатын салдар;
 - тепе-теңдік кванторы, тек сол жағдайда;
- тепе-теңдік кванторы, тек сол жағдайда;
 - қатаң енгізу кванторы.
- қатаң енгізу кванторы.
Жиынға енетін элементтер саны шенеулі немесе шексіз көп болуы мүмкін.
1-мысал: а) қазақ алфавитінің әріптер жиыны (42 элемент бар) ;
ә) натурал сандар жиыны (
 элементі бар) ;
элементі бар) ;
б)
 теңдеуінің нақты түбірлерінің жиыны ешқандай да элементтен тұрмайды, бос жиын.
теңдеуінің нақты түбірлерінің жиыны ешқандай да элементтен тұрмайды, бос жиын.
Ақырлы жиын деп осы жиынның элементтерінің санына тең болатын натурал сан табылатын жиынды айтады. Ақырлы емес жиын ақырсыз жиын деп аталады.
Ақырлы А және В жиындары тек қана бірдей элементтерден құралса, тең жиындар деп аталып, А=В деп белгіленеді.
Егер ақырлы А жиынында ақырлы В жиынына тиісті емес элемент бар болса, және керісінше, онда олар тең емес жиындар деп аталады.
2-мысал.
{0, 1, 2}={1, 2, 0}, {0, 1}
 {1, 2, 0, 3}.
{1, 2, 0, 3}.
Жиындардың берілу тәсілдері.
1. Мүшелерін (элементтерін) тізіп жазу арқылы. Ақырлы жиын
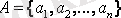 , ақырсыз жиын В={1, 3, 5, 7, . . . , } - тақ сандар жиыны.
, ақырсыз жиын В={1, 3, 5, 7, . . . , } - тақ сандар жиыны.
2. Сипаттау арқылы. Мысалы жиынның кез келген х мүшесі р(х)
қасиетіне ие болсын, онда осы элементтерден тұратын С жиыны былай беріледі: С={х
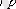 (х) }.
(х) }.
Осы сияқты анықталған жиындар
Q={
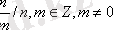 }, В={х: х=
}, В={х: х=
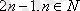 }.
}.
А және В жиындары берілсін. Егер А жиынының кез келген х элементі В жиынында да жатса, онда А жиыны В жиынының ішкі жиыны деп аталады.
А
 В немесе В
В немесе В
 А деп белгіленеді. Кванторлар тілінде
А деп белгіленеді. Кванторлар тілінде
(А
 В)
В)
 (х
(х
 А
А
 х
х
 В) .
В) .
Егер В жиынының А ішкі жиыны В жиынынан және Ø-ден өзгеше болса,
онда ол
меншікті ішкі жиыны
деп аталады. Кванторлар тілінде, А
 В
В

А
 В және А
В және А
 В.
В.
Ø кез келген жиынның ішкі жиыны болады: Ø
А.
Қасиеттері:
а) А
 А;
А;
ә) А
 В, В
В, В
 А
А
 А = В;
А = В;
б) А
 В, В
В, В
 С
С
 А
А
 С.
С.
В жиынының В және Ø ішкі жиындары оның меншіксіз ішкі жиындары деп аталады. Егер жиын ең болмағанда екі элементтен тұрса, онда оның меншікті ішкі жиындары болады.
Мысалы: А = {а, в} жиынының ішкі жиындары: {а}, {в}, {Ø}, {а, в}. Бұл ішкі жиындардың ішінде {а}, {в}- меншікті, ал {а, в}, {Ø}- меншіксіз болып табылады.
Ішкі жиындарға қолданылатын амалдар
U (универсум) деп кең жиынды белгілейік, яғни элементтер осы жиыннан алынып отыратын болсын.
Эйлер
 - Венн
- Венн
 диаграммасы
. Тік төртбұрыштың нүктесі U жиынынан алынған деп есептейік. Мысалға А={1, 2, 3, 4}, В={1, 3, 5}, С={5, 6} жиындарын алайық.
диаграммасы
. Тік төртбұрыштың нүктесі U жиынынан алынған деп есептейік. Мысалға А={1, 2, 3, 4}, В={1, 3, 5}, С={5, 6} жиындарын алайық.
1. Ең болмағанда А жиынына немесе В жиынына тиісті элементтер
жиынын А және В жиындарының
бірігуі
(қосындысы) (А
 В) деп айтады.
В) деп айтады.
А
В = {х: х
А немесе х
В}
А
 В={1, 2, 3, 4, 5}, А
В={1, 2, 3, 4, 5}, А
 С={1, 2, 3, 4, 5, 6}.
С={1, 2, 3, 4, 5, 6}.
1. 1 Сурет
 Леонард Эйлер (1707-1783) - швейцарлық математик.
Леонард Эйлер (1707-1783) - швейцарлық математик.
 Джон Венн (1834-1923) - ағылшын математигі.
Джон Венн (1834-1923) - ағылшын математигі.
«Бірігу» амалын жалпыласақ,
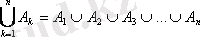
2.
А жиынына да, В жиынына да тиісті элементтер жиынын А және В жиындарының
қиылысуы
(көбейтіндісі) (А
 В) деп айтады.
В) деп айтады.
А
 В ={х:х
В ={х:х
 А және х
А және х
 В}.
В}.
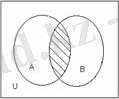
А
 В={1, 3}, В
В={1, 3}, В
 С={5}, А
С={5}, А
 С= Ø.
С= Ø.
1. 2 Сурет
«Қиылысу» амалын жалпыласақ,
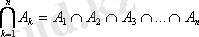 .
.
3. А жиынына тиісті, бірақ В жиынына тиісті емес элементтер жиынын А және В жиынының айырымы (А\В) деп айтады.
А\В = {х:х
 А және х
А және х
 В}
В}
А \ В={2, 4}, В \ С={1, 3}, А\С=А.
1. 3 Сурет
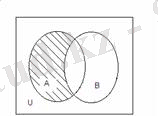
4.
А және В жиындарының
симметриялық айырмасы
(А
 В) деп келесі
В) деп келесі
жиынды айтады:
А
 В=(А\В)
В=(А\В)
 (В\А) = {х:(х
(В\А) = {х:(х
 А және х
А және х
 В) немесе (х
В) немесе (х
 В және х
В және х
 А) }.
А) }.
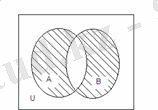
1. 4 Сурет
А
 В= {2, 4}
В= {2, 4}
 {5}={2, 4, 5}, А
{5}={2, 4, 5}, А
 C= {1, 2, 3, 4}
C= {1, 2, 3, 4}
 {5, 6}={1, 2, 3, 4, 5, 6}.
{5, 6}={1, 2, 3, 4, 5, 6}.
5.
U\A жиыны А жиынының
толықтауышы
деп аталып,
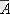 деп белгіленеді.
деп белгіленеді.
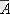 = U\A
= U\A
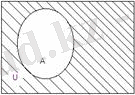
1. 5 Сурет
Унивесум U={1, 2, 3, 4, 5, 6, 7, 8, 9} болса, онда
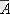 ={5, 6, 7, 8, 9} болады.
={5, 6, 7, 8, 9} болады.
1. 2 Жиындар алгебрасы
Жиындарға амалдар қолданып, жаңа жиындар алуға болады. Осы амалдардың негізгі қасиеттері мен олардың арасындағы байланыс жиындар алгебрасы деп аталады.
1. 1 К е с т е - Қасиеттер


(идемпотенттік)
А
 А=А
А=А
А
 А=А
А=А
Ауыстырымдылық (коммутативтік)
А
 В=В
В=В
 А
А
А
 В=В
В=В
 А
А
Үлестірімділік
А
 (В
(В
 С) =(А
С) =(А
 В)
В)
 С
С
А
 (В
(В
 С) =(А
С) =(А
 В)
В)
 С
С
Терімділік (дистрибутивтік)
А
 (В
(В
 С) =(А
С) =(А
 В)
В)
 (А
(А
 С)
С)
А
 (В
(В
 С) =(А
С) =(А
 В)
В)
 (А
(А
 С)
С)
Сіңіру
А
 (В
(В
 А) =А
А) =А
А
 (В
(В
 А) =А
А) =А
 Ø=А
Ø=А
 Ø= Ø
Ø= Ø
 U= U
U= U
 U= А
U= А
Қосалқы принципі (де Морган
 заңы)
заңы)
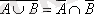
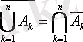
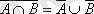
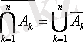
Екі рет теріске шығару
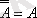
Толықтауыштың қасиеті
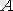
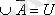
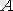
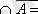 Ø
Ø
Жиындар арасындағы қасиеттер (заңдар) жоғарыдағы келтірілген қасиеттермен шектеліп қоймайды. Қалған қасиеттерді логика алгебрасының ережелері бойынша аталған касиеттерді қолданып алуға болады.
Жиындардың декарттық (тура) көбейтіндісі
Математикада жиындардың жай элементтері ғана емес, сонымен бірге олардың реттелген жұп элементтері де кездеседі. (а 1 , а 2 , . . . , а n ) элементтері реттелген жиын берілсін, оны жиынтық, вектор, кортеж деп те атайды, а і -
 Огастес де Морган (1806-1871) - шотландық математик
Огастес де Морган (1806-1871) - шотландық математик
жиынның і-ші мүшесі. (а 1 , а 2 , . . . , а n ) - жиынтығының ұзындығы деп n компоненталар санын айтамыз.
А және В жиындарының
тура немесе декарттық көбейтіндісі
деп (а, в) жұбының жиынын айтамыз.
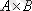 деп белгілейміз.
деп белгілейміз.
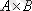 ={(a, b) : a
={(a, b) : a

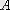 , b
, b

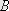 },
},
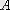 =
=
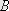
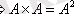 ,
,
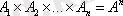 ,
,
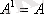 ,
,
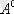 {Ø}.
{Ø}.
Мысалдар қарастырып өтейік.
1. A={1, 2}, B={1, 2, 3} жиындары берілсін. Бұл жиындар үшін тура көбейтінділер
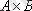 {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3) },
{(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3) },
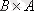 {(1, 1), (1, 2), (2, 1), (2, 2), (3, 1), (3, 2) },
{(1, 1), (1, 2), (2, 1), (2, 2), (3, 1), (3, 2) },
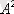 {(1, 1), (1, 2), (2, 1), (2, 2) } (2, 1)
{(1, 1), (1, 2), (2, 1), (2, 2) } (2, 1)
 (1, 2) .
(1, 2) .
2. R - нақты сандар жиыны берілсін. Онда
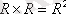 {(x, y}: (x, y) - жазықтықтың нүктелері},
{(x, y}: (x, y) - жазықтықтың нүктелері},
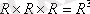 {(x, y, z) : (x, y, z) - кеңістіктің нүктелері}.
{(x, y, z) : (x, y, z) - кеңістіктің нүктелері}.
3.
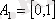 ,
,
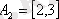 екі жиынды қарастырайық. Егер жазықтықтағы декарттық координаталар жүйесін қарастырсақ, онда
екі жиынды қарастырайық. Егер жазықтықтағы декарттық координаталар жүйесін қарастырсақ, онда
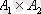 ұзындығы бірге тең квадрат ретінде қарастыруға болады.
ұзындығы бірге тең квадрат ретінде қарастыруға болады.
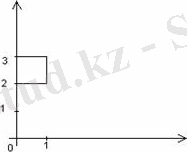
1. 6 Сурет
1-есеп
.
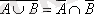 де Морган заңын (қосалқы принципі) дәлелдеу керек.
де Морган заңын (қосалқы принципі) дәлелдеу керек.
Шешуі: І әдіс Эйлер-Венн диаграммасы арқылы. Ол үшін теңдіктің сол жағындағы жиынды кескіндеп аламыз:
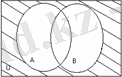 а)
а)

1. 7 Сурет
 Ал оң жақтағы жиынды бейнелеу үшін алдымен
Ал оң жақтағы жиынды бейнелеу үшін алдымен
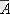 жиынын
жиынын
 көлденең жолақпен,
көлденең жолақпен,
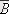 жиынын тік жолақпен белгілеп аламыз. Сонда бізге керекті жиын осы екі жолақтың қиылысуында, яғни тормен кескінделген жиын болады;
жиынын тік жолақпен белгілеп аламыз. Сонда бізге керекті жиын осы екі жолақтың қиылысуында, яғни тормен кескінделген жиын болады;
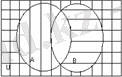 ә)
ә)
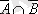
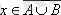
1. 8 Сурет
Байқасақ, жоғарыдағы диаграммада штрихпен белгіленген жиын мен төмендегі тормен белгіленген жиын бір жиынды береді, бұл екі жиынның теңдігін білдіреді.
ІІ әдіс қасиеттерге сүйеніп, өрнектерді түрлендіру арқылы.
Алдымен U =V
 U
U
 V, V
V, V
 U қасиеті бойынша:
U қасиеті бойынша:
1)
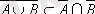 ;
;
2)
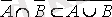 енгізулері орындалатынын көрсетейік.
енгізулері орындалатынын көрсетейік.
1)
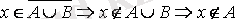 және
және
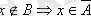 және
және
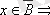
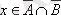 ;
;
2) керісінше,
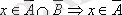 және
және
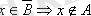 және
және
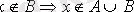

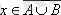 .
.
Жиынның бүркеуі мен бөлікшесі
Жиындарға қолданылатын операциялардың тағы бір түрі - жиынды ішкі жиындар жүйесіне бөліктеу операциясы болып табылады. А жиыны мен оның ішкі жиындар жүйесін A
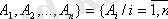 қарастырайық.
қарастырайық.
Анықтама.
Егер 1)
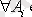 A
A
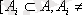 Ø], 2)
Ø], 2)
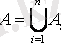
шарттары орындалса, онда A жиын жүйесін А жиынының бүркеуі деп атайды.
Анықтама.
Егер 1)
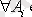 A
A
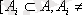 Ø,
Ø,
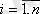 ] ; 2)
] ; 2)
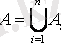 ;
;
3)
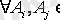 A
A
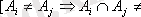 Ø] немесе
Ø] немесе
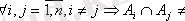 Ø
Ø
шарттары орындалса, онда A жиын жүйесі А жиынының бөлікшесі деп аталады.
Егер бүркеу анықтамасындағы екі шартқа 3) шартты қоссақ, онда бүркеу бөлікше бола алады. Басқаша айтқанда, егер әрбір
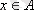 элементі тек қана бір А
і
ішкі жиынына тиісті болса, онда А жиынының бос емес ішкі жиындардың A жүйесі оның бөлікшесі бола алады.
элементі тек қана бір А
і
ішкі жиынына тиісті болса, онда А жиынының бос емес ішкі жиындардың A жүйесі оның бөлікшесі бола алады.
1-мысал.
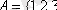 жиыны берілсін:
жиыны берілсін:
а)
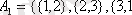 - А жиынының бүркеуі;
- А жиынының бүркеуі;
ә)
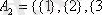 - А жиынының бөлікшесі болады;
- А жиынының бөлікшесі болады;
б)
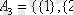 - қандай-да бір ішкі жиындардың жүйесі, ол бүркеуі де емес, бөлікшесі де емес, себебі
- қандай-да бір ішкі жиындардың жүйесі, ол бүркеуі де емес, бөлікшесі де емес, себебі
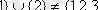 .
.
2-мысал. N - натурал сандар жиынын қарастырайық. N 0 - жұп, N 1 - тақ сандар жиыны болсын. Онда {N 0 , N 1 } -N бөлікшесі бола алады.
1. 3 Қатынастар. Унарлы, бинарлы, n-орынды қатынастар
А
1
, А
2
, . . . , А
n
жиындарындағы n - орынды қатынас немесе n - орынды предикат деп А
1
 А
2
А
2
 . . .
. . .
 А
n
тура көбейтіндісінің кез келген жиыншасын айтамыз. Басқаша айтқанда, егер (х
1
, х
2, . . . ,
x
n
)
А
n
тура көбейтіндісінің кез келген жиыншасын айтамыз. Басқаша айтқанда, егер (х
1
, х
2, . . . ,
x
n
)
 Р болса, х
1
, х
2, . . . ,
x
n
элементтері (мұндағы х
1
Р болса, х
1
, х
2, . . . ,
x
n
элементтері (мұндағы х
1
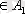 ,
х
2
,
х
2
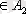 ,
x
n
,
x
n
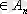 )
Р
қатынасымен байланыстырылған
деп аталып, Р(х
1
, х
2, . . . ,
x
n
)
деп белгіленеді.
)
Р
қатынасымен байланыстырылған
деп аталып, Р(х
1
, х
2, . . . ,
x
n
)
деп белгіленеді.
n=1 болса, онда Р қатынасы А жиынының жиыншасы болады, Р
 А және
унарлы
қатынас
немесе қасиет деп аталады.
А және
унарлы
қатынас
немесе қасиет деп аталады.
n=2 болса, онда
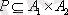 жиі кездесетін екі орынды қатынас. Бұл жағдайда олар
бинарлы қатынас
немесе сәйкестік деп аталады. Сонымен А және В жиындарының арасындағы Р сәйкестігі А
жиі кездесетін екі орынды қатынас. Бұл жағдайда олар
бинарлы қатынас
немесе сәйкестік деп аталады. Сонымен А және В жиындарының арасындағы Р сәйкестігі А
 В жиынының жиыншалары болып табылады,
В жиынының жиыншалары болып табылады,
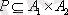 және (х, у)
және (х, у)
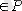 ,
оны жиі хРу деп жазады.
,
оны жиі хРу деп жазады.
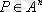 - А жиынындағы
n-орынды қатынас
. Кейбір оқулықта
- А жиынындағы
n-орынды қатынас
. Кейбір оқулықта
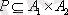 бинарлық қатынасы
бинарлық қатынасы
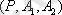 немесе
немесе
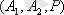 деп белгіленеді, А
1
- қатынасты жіберу облысы, А
2
- қатынасты қабылдау жиыны деп аталады.
деп белгіленеді, А
1
- қатынасты жіберу облысы, А
2
- қатынасты қабылдау жиыны деп аталады.
1-мысал:
а) егер
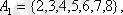 ал бинарлық қатынас P={(x; y) / x, y
ал бинарлық қатынас P={(x; y) / x, y
 , y элементі х-ке бөлінеді, х
, y элементі х-ке бөлінеді, х
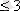 }, онда P={(2, 2), (2, 4), (2, 6), (2, 8), (3, 3), (3, 6) };
}, онда P={(2, 2), (2, 4), (2, 6), (2, 8), (3, 3), (3, 6) };
ә) P={(х, у) / x, y
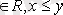 } қатынасын R жиынында қарастырайық. Онда xPy жазуын
} қатынасын R жиынында қарастырайық. Онда xPy жазуын
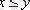 деп түсінуге болады, яғни Р қатынасы “
деп түсінуге болады, яғни Р қатынасы “
 ” символымен берілген;
” символымен берілген;
б) А - нақты сандар жиыны, онда {(x, y)
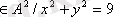 } A жиынындағы бинарлы қатынас болады;
} A жиынындағы бинарлы қатынас болады;
в) А - адамдар жиыны, онда {(x, y)
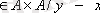 -тің туысқаны} А-дағы бинарлық қатынас.
-тің туысқаны} А-дағы бинарлық қатынас.
Бинарлы қатынастардың берілу жолдары:
1) тізіп жазу арқылы, мысалы (2, 2), (2, 4), (2, 6), (2, 8), (3, 3), (3, 6) ;
2)
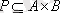 бинарлық қатынасын график көмегімен кескіндеу қолайлы.
бинарлық қатынасын график көмегімен кескіндеу қолайлы.
Өзара перпендикуляр өстер (Ox - көлденең өс, Oy - тік өс) сызайық. А және В жиындарының элементтерін сәйкес өстерде белгілейік. XOY жазықтығында координаталары
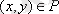 болатын нүктелерді белгілейік. Алынған нүктелер жиыны Р қатынасына сәйкес келеді;
болатын нүктелерді белгілейік. Алынған нүктелер жиыны Р қатынасына сәйкес келеді;
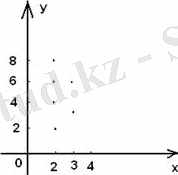
1. 9 Сурет
1 мысалдағы Р қатынасы.
3) Р қатынасымен байланысқан
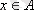 және
және
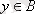 элементтері стрелкамен қосылған түрінде.
элементтері стрелкамен қосылған түрінде.
2
-м
ысал.
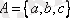 мен
мен
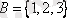 жиындарының арасындағы
жиындарының арасындағы
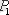 қатына-сын, ал А жиынындағы
қатына-сын, ал А жиынындағы
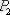 қатынасын бейнелеу керек:
қатынасын бейнелеу керек:
а)
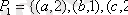 ;
;
ә)
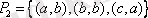 ;
;
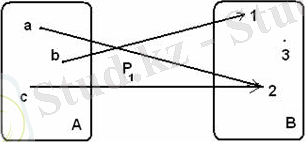
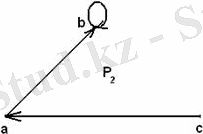
1. 10 Сурет
4) ақырлы жиындардың арасындағы бинарлы қатынас жұптардың тізімімен немесе матрица арқылы беріледі.
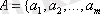 ,
,
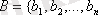 және
және
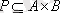 бинарлы қатынасы берілген болсын. Бұл
қатынастың матрицасы
:
бинарлы қатынасы берілген болсын. Бұл
қатынастың матрицасы
:
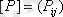 ,
,
 өлшемді, мұндағы
өлшемді, мұндағы
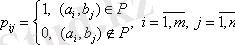 .
.
Сонымен нөл мен бірден тұратын кез келген матрица - қандай да бір бинарлы қатынастың матрицасы болып табылады.
3-мысал.
а)
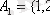 ,
,
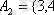 жиындары мен осы жиындар арасындағы
жиындары мен осы жиындар арасындағы
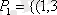 ,
,
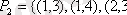 қатынастары берілген. Бұл қатыныстарды матрица арқылы беруге болады
қатынастары берілген. Бұл қатыныстарды матрица арқылы беруге болады
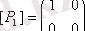 ,
,
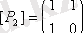 ;
;
ә)
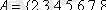 жиынында
жиынында
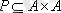 қатынасы берілген:
қатынасы берілген:
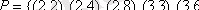 . Бұл қатынасқа сәйкес матрица
. Бұл қатынасқа сәйкес матрица
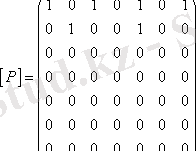 .
.
Анықтама.
Р қатынасының
анықталу облысы
(D
p
деп белгіленеді) D
p
 кейбір у үшін
кейбір у үшін
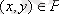 . Ал
мәндерінің жиыны
Е
р
. Ал
мәндерінің жиыны
Е
р
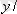 кейбір х үшін
кейбір х үшін
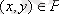 жиындары айтылады.
жиындары айтылады.
D p - бірінші элементтерден құралған жиын,
Е р - екінші элементтерден құралған жиын.
А және В жиындарының арасында Р қатынасы берілсін.
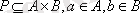 .
.
Келесі анықтамаларды енгізейік:
а) кері қатынас :
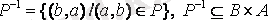 ;
;
ә) толықтауыш қатынас :
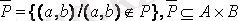 ;
;
б) тепе-тең қатынас :
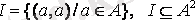 . Кейде
. Кейде
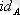 деп белгіленеді,
деп белгіленеді,
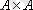 -дағы диагональ деп те атайды;
-дағы диагональ деп те атайды;
в) универсалды қатынас :
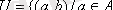 және
және
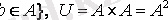 кейде толық қатынас деп те атайды.
кейде толық қатынас деп те атайды.
4-мысал.
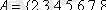 жиынында
жиынында
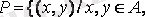 x элементі y -тің бөлгіші} қатынасы берілген. Олай болса
x элементі y -тің бөлгіші} қатынасы берілген. Олай болса
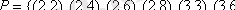 . Бұл қатынас үшін D
p
={2, 3} - анықталу облысы, E
p
={2, 3, 4, 6, 8} - мәндерінің жиыны, P
-1
={(2, 2), (4, 2), (6, 2), (8, 2), (3, 3), (6, 3) } - кері қатынас.
. Бұл қатынас үшін D
p
={2, 3} - анықталу облысы, E
p
={2, 3, 4, 6, 8} - мәндерінің жиыны, P
-1
={(2, 2), (4, 2), (6, 2), (8, 2), (3, 3), (6, 3) } - кері қатынас.
1. P қатынасына (предикатына) қатысты Х жиынының
бейнесі
деп, келесі жиын айтылады: P(x) ={y/(x, y)
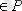 , кейбір
, кейбір
 үшін}
үшін}
2. P предикатына қатысты кері бейнесі деп, Р -1 (х) немесе Р -1 предикатына қатысты Х жиынының бейнесін айтады.
Анықтама.
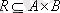 және
және
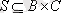 бинарлық қатынастарының
композициясы
немесе
көбейтіндісі
деп
бинарлық қатынастарының
композициясы
немесе
көбейтіндісі
деп
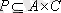 қатынасы
қатынасы
 немесе жиыны айтылады, ол былай анықталады
немесе жиыны айтылады, ол былай анықталады
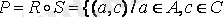 және
және
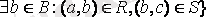 .
.
5-мысал
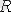 және
және
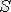 - оң бүтін сандар жиынында берілген бинарлық қатынастар болсын:
- оң бүтін сандар жиынында берілген бинарлық қатынастар болсын:
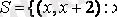 -оң бүтін сан},
-оң бүтін сан},
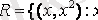 - оң бүтін сан}. Онда
- оң бүтін сан}. Онда
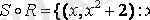 - оң бүтін сан} және
- оң бүтін сан} және
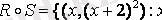 - оң бүтін сан}.
- оң бүтін сан}.
Теорема. Кез келген P, Q, R бинарлық қатынастар үшін келесі қасиеттер орындалады:
а)
;
ә)
;
б)
.
Дәлелдеуі [1, 19 бет] .
Бинарлық қатынас матрицасының негізгі қасиеттері
Егер
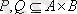 және
және
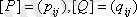 , онда
, онда
1.
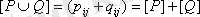
(матрицалардың элементтерін қосу 0+0=0; 1+1=0+1=1+0=1 ережесі бойынша жүргізіледі) ;
2.
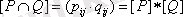
матрицалардың элементтерін көбейту кәдімгідей іске асырылады, яғни 0
 0=0
0=0
 1=1
1=1
 0=0; 1
0=0; 1
 1=1) .
1=1) .
1-мысал.
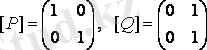 бинарлық қатынастардың матрицалары берілген. Олар үшін
бинарлық қатынастардың матрицалары берілген. Олар үшін
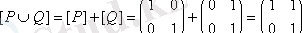 ,
,
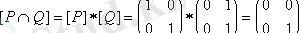 .
.
3. Егер
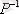 -кері қатынас болса, онда
-кері қатынас болса, онда
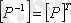 .
.
4. Егер
 және
және
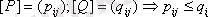 .
.
5.
 -тепе-тең қатынас болса, онда
-тепе-тең қатынас болса, онда
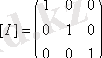 - бірлік матрица.
- бірлік матрица.
6.
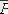
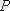 -ның толықтауышы, онда
-ның толықтауышы, онда
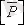 - бұл
- бұл
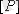 -дағы 0-ді 1-ге, ал 1-ді 0-ге ауыстырған матрица.
-дағы 0-ді 1-ге, ал 1-ді 0-ге ауыстырған матрица.
7. Егер
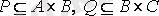 , онда композиция
, онда композиция
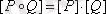 және матрицалар кәдімгі матрицаларды көбейту ережесі бойынша іске асырылады, бірақ матрицаларды көбейту кезінде элементтерді қосып, көбейту бірінші пункттегідей жүргізіледі
және матрицалар кәдімгі матрицаларды көбейту ережесі бойынша іске асырылады, бірақ матрицаларды көбейту кезінде элементтерді қосып, көбейту бірінші пункттегідей жүргізіледі
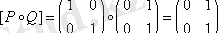 .
.
Анықтама.
P қатынасы
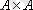 анықталған болсын.
анықталған болсын.
1. Егер
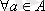 үшін
үшін
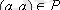 болса, онда P
рефлексивті
қатынас деп аталады (P-«бір қалада тұру») .
болса, онда P
рефлексивті
қатынас деп аталады (P-«бір қалада тұру») .
2. Егер
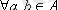 үшін
үшін
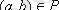 -дан
-дан
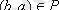 шығатын болса, онда P
симметриялы
қатынас деп аталады (P-«бір фирмада жұмыс істеу») .
шығатын болса, онда P
симметриялы
қатынас деп аталады (P-«бір фирмада жұмыс істеу») .
3. Егер
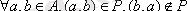 -дан
-дан
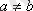 шығатын болса, онда P
антирефлексивті
деп аталады (P-«ұлы болу») .
шығатын болса, онда P
антирефлексивті
деп аталады (P-«ұлы болу») .
4. Егер
 және
және
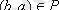 -дан
-дан
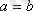 шығатын болса, онда P
антисимметриялы
қатынас деп аталады (P-«бастық болу») .
шығатын болса, онда P
антисимметриялы
қатынас деп аталады (P-«бастық болу») .
5. Егер
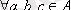
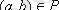 және
және
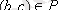 -да
-да
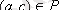 шығатын болса, онда Р
транзитивті
қатынас деп аталады (P-«ағасы болу» немесе
шығатын болса, онда Р
транзитивті
қатынас деп аталады (P-«ағасы болу» немесе
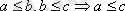 ) .
) .
2-мысал.
А- нақты оң сандар жиыны болсын. Р қатынасы ретінде
 ”<”, “>”, “=” қарастыруға болады.
”<”, “>”, “=” қарастыруға болады.
Ескерте кетелік, Р бинарлы қатынасы
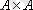 жиынында анықталған болсын. Бұл қатынастың қасиеттерін матрицасы арқылы тексеруге болады:
жиынында анықталған болсын. Бұл қатынастың қасиеттерін матрицасы арқылы тексеруге болады:
1. P- рефлексивті болсын
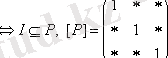 ,
,
 мұнда
мұнда

 орнына бір немесе нөлдер белгіленген.
орнына бір немесе нөлдер белгіленген.
2. P- симметриялы болсын
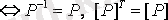 .
.
3. P- антисимметриялы
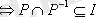 немесе
немесе
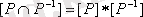 . Бұл қасиет
. Бұл қасиет
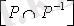 матрицасындағы бас диагональдан басқа жердегі элементтері нөлге тең болады, бас диагональда да нөлдер болуы мүмкін екендігін көрсетеді.
матрицасындағы бас диагональдан басқа жердегі элементтері нөлге тең болады, бас диагональда да нөлдер болуы мүмкін екендігін көрсетеді.

4. P- транзитивті
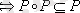 , яғни егер
, яғни егер
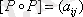 ,
,
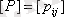 , онда
, онда
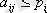 .
.
3-мысал.
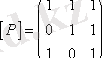 матрицасымен берілген Р қатынасының қасиеттерін қарастырайық.
матрицасымен берілген Р қатынасының қасиеттерін қарастырайық.
 матрицасының бас диагоналінде бірлер тұрғандықтан, Р рефлексивті, яғни
матрицасының бас диагоналінде бірлер тұрғандықтан, Р рефлексивті, яғни
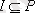 .
.
 матрицасы симметриялы емес, олай болса Р қатынасы да симметриялы емес.
матрицасы симметриялы емес, олай болса Р қатынасы да симметриялы емес.
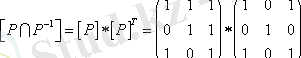 .
.
Бұл матрица антисимметриялылықты тексеруге қажет. Бас диагональдан басқа жердегі элементтер нөлге тең емес болғандықтан, Р антисимметриялы емес. Келтірілген мысалдан антисимметриялық қасиет пен симметриялы емес қасиеттері әртүрлі екендігі көрінеді. Енді транзитивті қасиетіне тексерейік.
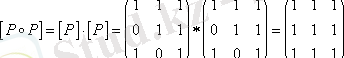
яғни
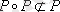 , олай болса транзитивті емес [4, 93 бет], [6, 13 бет] .
, олай болса транзитивті емес [4, 93 бет], [6, 13 бет] .
Егер
P қатынасы рефлексивті, симметриялы және транзитивті болса, онда ол
эквивалентті қатынас
деп аталады. Эквиваленттілікті Е немесе ~ (тильда) символымен белгілейді:
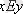 ,
,
 .
.
4-мысал.
«
 » теңдік қатынасы кез келген А жиынында эквивалентті қатынас болады, себебі:
» теңдік қатынасы кез келген А жиынында эквивалентті қатынас болады, себебі:
а) рефлексивті
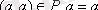 ;
;
ә) симметриялы
 ,
,
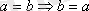 ;
;
б) транзитивті
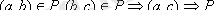 ,
,
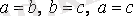 .
.
5-мысал. Үшбұрыштар жиынын алсақ, ұқсастық қатынасы эквивалентті болады.
А жиынындағы Е эквиваленттілік қатынасы осы А жиынын элементтері өзара эквивалентті ішкі жиындарға бөледі. Мұндай ішкі жиындар эквиваленттілік класы деп аталады.
Е - А жиынындағы эквиваленттілік қатынасы және
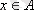 болсын. А жиынының х-ке эквивалентті элементтердің ішкі жиыны х элементінің эквиваленттілік класы деп аталады. Е(х) немесе
болсын. А жиынының х-ке эквивалентті элементтердің ішкі жиыны х элементінің эквиваленттілік класы деп аталады. Е(х) немесе
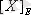 деп белгіленеді
деп белгіленеді
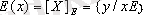
Эквивалент кластар жиыны А жиынының Е эквивалентке қатысты
фактор жиыны
деп аталады,
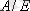 деп белгіленеді:
деп белгіленеді:
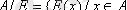 . Фактор жиын булеанның ішкі жиыны болып табылады.
. Фактор жиын булеанның ішкі жиыны болып табылады.
6-мысал. А - АЭжБИ студенттер жиыны, Е - студенттік группаға тиесілік қатынасы. Эквиваленттілік класы - бір группадағы студенттер жиыны. Е-ге қатысты АЭжБИ студенттер жиынындағы фактор жиын АЭжБИ студенттік топтар жиыны болады.
Анықтама бойынша:
а) эквиваленттілік класының кез келген элементі эквиваленттілік класын туындайды, яғни егер
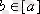 , онда
, онда
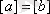 ;
;
ә) әрбір эквиваленттілік класта кем дегенде бір элемент бар, яғни
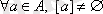 ;
;
б) ешқандай элемент екі әртүрлі класқа бірден тиесілі бола алмайды
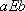 , онда
, онда
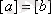
Бөлікше анықтамасын еске түсірсек, онда
Теорема.
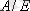 фактор-жиын А жиынының бөлікшесі болып табылады.
Керісінше, егер A
фактор-жиын А жиынының бөлікшесі болып табылады.
Керісінше, егер A
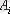 - А жиынының қандай-да бір бөлікшесі, онда оған сәйкес Е эквиваленттілік қатынасын
- А жиынының қандай-да бір бөлікшесі, онда оған сәйкес Е эквиваленттілік қатынасын
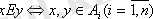 орнатуға болады.
орнатуға болады.
Сонымен, А жиынындағы барлық эквиваленттік қатынасы мен А-дағы барлық бөлікшелер арасында өзара бірмәнді сәйкестік орнатуға болады.
7-мысал.
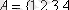 жиыны берілсін.
жиыны берілсін.
A
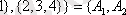 -
-
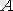 бөлікшесі, ал
бөлікшесі, ал
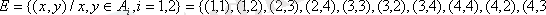 -
-
осы бөлікшеге сәйкес эквиваленттік қатынас болады.
8-мысал.
 жиыны берілсін.
жиыны берілсін.
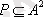 және
және
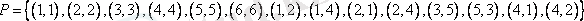 болсын:
болсын:
а)
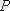 қатынасының эквивалентті қатынас болатындығын көрсетейік, яғни бұл қасиет рефлексивті, симметриялы және транзитивті қасиеттерге ие болатын-дығын тексереміз. Ол үшін
қатынасының эквивалентті қатынас болатындығын көрсетейік, яғни бұл қасиет рефлексивті, симметриялы және транзитивті қасиеттерге ие болатын-дығын тексереміз. Ол үшін
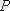 қатынасының матрицасын құрамыз
қатынасының матрицасын құрамыз
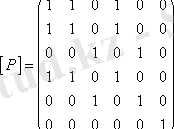 .
.
1)
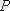 - рефлексивті, себебі матрицадағы бас диагональда бірлер тұр;
- рефлексивті, себебі матрицадағы бас диагональда бірлер тұр;
2)
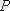 - симметриялы, себебі
- симметриялы, себебі
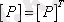 ;
;
3)
 .
.
Сондықтан
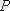 - транзитивті. Олай болса,
- транзитивті. Олай болса,
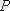 - эквивалентті қатынас;
- эквивалентті қатынас;
ә) эквиваленттілік класы мен барлық эквиваленттілік кластарының жиынын (яғни
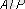 фактор-жиынын құрайық) .
фактор-жиынын құрайық) .
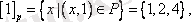
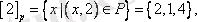
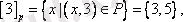
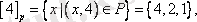
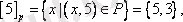
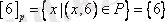
Сонымен үш эквиваленттілік класы бар
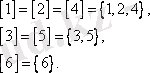
Сондықтан фактор-жиын
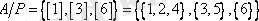 . Сонымен берілген эквивалентті қатынасқа сәйкес А жиынының бөлікшесін алдық.
. Сонымен берілген эквивалентті қатынасқа сәйкес А жиынының бөлікшесін алдық.
Бұл мысалдан:
а) эквиваленттілік класының кез келген элементінен эквиваленттілік класс туындайды (яғни
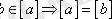 ) ;
) ;
ә) әрбір эквиваленттілік класында ең болмағанда бір элемент болу керек (яғни
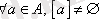 ) ;
) ;
б) әр элемент тек бір ғана класқа тиесілі болу керек (
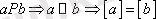 ) .
) .
1. 4 Реттік қатынастар
Егер А жиынында Р қатынасы антисимметриялы және транзитивті болса, ол
реттік қатынас
деп аталады. Реттік қатынас рефлексивті болса, онда ол
дербес реттілік
(қатаң емес, мысалы
 ), ал антирефлексивтік қосылса, онда
қатаң реттілік
(қатаң, мысалы,
), ал антирефлексивтік қосылса, онда
қатаң реттілік
(қатаң, мысалы,
 ) деп аталады.
) деп аталады.
А жиынында реттік қатынас берілген болсын. Егер осы жиынның екі
 ,
,
 элементтері үшін
элементтері үшін
 немесе
немесе
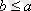 орындалса, онда бұл элементтер
салыстырмалы
деп аталады, қарсы жағдайда
салыстырылмайтын
деп аталады.
орындалса, онда бұл элементтер
салыстырмалы
деп аталады, қарсы жағдайда
салыстырылмайтын
деп аталады.
Егер А жиынының кез келген екі элементі салыстырылмалы болса, онда осы жиындағы дербес реттілік сызықты (толық, тізбектей) деп аталады.
Дербес (сызықты) реттілік анықталған жиын дербес реттелген жиын (сызықты реттелген жиын) деп аталып, д. р. ж. (с. р. ж) деп белгіленеді.
1-мысал.
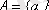 жиыны берілсін:
жиыны берілсін:
а)
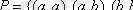 - дербес реттілік қатынас.
- дербес реттілік қатынас.
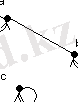 Ол сызықты болмайды, себебі
Ол сызықты болмайды, себебі
 және
және
 ,
,
 және
және
 арасында қатынас жоқ, салыстыруға келмейді.
арасында қатынас жоқ, салыстыруға келмейді.
1. 11 Сурет
Оның матрицасы
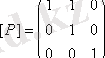 - бірлік матрица, рефлексивті (тепе-тең) ;
- бірлік матрица, рефлексивті (тепе-тең) ;
ә) P(A)
 Ø,
Ø,
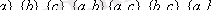 .
.
Осы P(A) жиынында келесі қатынасты анықтайық:
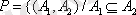
=
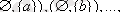
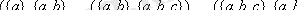
P(A) - дербес реттелген жиын болады, бірақ сызықты реттілік емес, себебі
 салыстырмалы, ал
салыстырмалы, ал
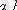 және
және
 салыстырылмайтын элементтер;
салыстырылмайтын элементтер;
б) сызықты реттелген жиын - бұл N, Z, Q, R жиындары (кәдімгі рет бойынша алынған “<”, “>”, “=”…) . Бұл сызықты реттелген жиынды <N,
 >, (Z,
>, (Z,
 ) жұбы ретінде белгілейді.
) жұбы ретінде белгілейді.
Сызықты реттелген жиынды бірінші элементіне қарай бөлуге болады. Мысалы, егер сызықты реттелген жиын ретінде натурал және бүтін сандар жиынын алатын болсақ, онда натурал сандарда кіші элемент бар, ал бүтін сандарда жоқ.
Егер реттелген А жиынында

 орындалатын х элементі болмаса,
орындалатын х элементі болмаса,
 элементі
минималды (максималды)
деп аталады.
элементі
минималды (максималды)
деп аталады.
Егер сызықты реттелген жиынның бос емес ішкі жиынында минимальды элемент бар болса, онда ол әбден реттелген деп аталады.
2-мысал.
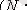 әбден реттелген жиын.
әбден реттелген жиын.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz