Өнеркәсіптік манипуляторлардың кинематикасы мен динамикасы: позицияларды кері есептеу және вектор-матрицалық әдістер


16-22 беттер
1. 2. Кинематика мен манипуляторлар динамикасының міндеттері
Кинематика мен манипуляторлар динамикасының міндеттері дизайнның әртүрлі кезеңдерінде және роботтарды басқаруда шешілуі керек. Әдетте өнеркәсіптік роботтарды жобалау кезінде шешілетін кинематика мен манипуляторлардың динамикасының негізгі міндеттерін қарастырыңыз. Өнеркәсіптік роботты жобалау, әдетте, роботты пайдалану жоспарланған операциялар мен өндіріс жағдайларын зерттеуден басталады. Нысанның қозғалысы, жылдамдығы, үдеуі зерттеледі: объектінің қозғалысының бұл шарттары Робот - манипулятордың атқарушы механизміне қойылатын талаптарды анықтайды.
Манипулятордың жетектеріне қойылатын талаптарды тұжырымдау үшін абсолютті координаттар жүйесіндегі объектінің қозғалысына қойылатын кинематикалық және геометриялық талаптар кинематикалық жұптардағы қозғалыстарға, жылдамдықтар мен үдеулерге қойылатын талаптар өзгертілуі керек. Осы мақсатта жолдар, жылдамдықтар мен үдеулер туралы кері есептер шешіледі. Позициялардың кері міндеті - манипулятор байланыстарының объектінің берілген позицияларына немесе онымен тығыз байланысты тәуелді сілтемеге қатысты салыстырмалы координаттарын анықтау. Жылдамдықтар туралы кері есеп кинематикалық жұптарда Шығыс байланысының берілген жылдамдығы бойынша қажетті жалпыланған жылдамдықты анықтау болып табылады.
Егер берілген сызықтық және бұрыштық жылдамдық векторларын ұстап алу қажет болса, онда мәселені біржақты шешу үшін манипулятордың кемінде алты еркіндік дәрежесі болуы керек екені анық. Бұл мәселені шешу жылдамдық пен беріліс қатынасы бойынша жетектерге қойылатын талаптарды тұжырымдауға мүмкіндік береді. Кинематикалық жұптарда талап етілетін үдеулер, әдетте, ұстап алудың берілген үдеуі бойынша анықталмайды, бірақ жетектердің қажетті күштерін анықтау мәселесі шешіледі.
берілген манипуляция қозғалысын жүзеге асыру үшін қажетті - тау немесе шығыс буынында берілген күш. Бұл 12] . есеп динамиканың бірінші немесе кері есебі деп аталады [12] . "Динамиканың кері есебі" термині "динамиканың бірінші есебі" терминіне қарағанда кеңірек [5] және басқару жүйесі мен басқару алгоритмдерінің құрылымы мен параметрлерін анықтау мәселелерін қамтиды. Жетектердегі күштерді, жалпыланған жылдамдықтар мен үдеулерді анықтағаннан кейін абсолютті жылдамдықтар мен сілтемелер массаларының үдеулерін және бұрыштық жылдамдықтар мен сілтемелер үдеулерін, олардың масса орталықтарындағы негізгі векторлар мен сілтемелер инерциясының негізгі сәттерін анықтауға болады. Соңғылары беріктікті есептеу үшін пайдаланылуы мүмкін. Барлық осы есептеулерді жобалаудың бастапқы кезеңінде белгісіз және инженердің тәжірибесі мен машиналар мен жүйелердің ұқсас түйіндерін жобалау тәжірибесі негізінде таңдалған геометриялық және инерциялық жұп - метр манипуляторлар болған кезде ғана жүргізуге болатындығы анық.
Осылайша, дизайн процесі итеративті болып табылады: біріншіден, техникалық талаптарға негізделген дизайнер кинематикалық схеманы және манипулятордың кейбір геометриялық параметрлерін таңдайды, содан кейін кері есептерді шеше отырып, жетектер мен басқару жүйесіне қойылатын талаптарды анықтайды, жетектерді және бүкіл атқарушы механизмді таңдайды немесе құрастырады. Содан кейін, берілген күштердің әсерінен манипулятордың қозғалысы туралы мәселені (тікелей мәселені) шеше отырып, дизайнер техникалық талаптарды орындауға сендіреді немесе манипулятордың дизайнын немесе басқару жүйесін өзгерту туралы шешім қабылдайды. Позициялар мен жылдамдықтар туралы кері есептерді шешудің нәтижелері кинематикалық басқару алгоритмдерін құрудың негізін құрайтынын атап өткен жөн: жылдамдық векторын басқару алгоритмдері мен алгоритмдері. Позициялық басқару алгоритмдері роботты оның кинематикалық схемасы негізінде берілген позицияға түсіру үшін жасалады. Жылдамдық векторын басқару алгоритмдері роботтың сызықтық және бұрыштық жылдамдық векторларының деректерін оның кинематикалық схемасы негізінде ұстап алуын хабарлау үшін жасалады.
Динамикалық басқару алгоритмдері жүйелердің динамикалық қасиеттерін ескереді және жүйенің тұрақтылығын ескере отырып, манипуляциялық роботтар динамикасының кері есептерін шешу негізінде құрылады [3, 19, 38] .
2-тарау
Манипуляторларды кинематикалық талдаудың векторлық әдісі өнеркәсіптік роботтарды жобалау және басқару мәселелерін шешуде оның байланыстарының бекітілген координаттар жүйесіне қатысты позицияларын - сілтемелердің абсолютті позицияларын және олардың салыстырмалы позицияларын - жалпыланған координаттарды анықтау қажет. Естеріңізге сала кетейік, бірінші тапсырма тікелей тапсырма деп аталады, ал екіншісі - манипулятордың позицияларына кері тапсырма. Белгілі жалпыланған координаттарда манипулятордың позициялары туралы тікелей есепті шешу сілтемелердің салыстырмалы позицияларын анықтайтын матрицаларды көбейтуге дейін азаяды немесе вектордың соңғы айналу формулаларын қолдану арқылы жүзеге асырылады.
Манипулятордың Шығыс байланысының берілген полотениясында жалпыланған координаттарды анықтау қиынырақ міндет болып табылады, өйткені бұл алгебралық теңдеулердің сызықтық емес жүйелерін шешумен байланысты. Манипулятордың позициялары туралы кері есепті шешудің тиімді әдісі-векторлық-матрицалық әдіс [31, 32] . Бұл әдісте берілген және белгісіз шамалар арасындағы байланыстардың негізгі шарттары векторлық формада қолданылады, ал векторлардың проекцияларын алдын - ала таңдау матрицалық формада жүзеге асырылады. Механизмдер теориясында векторлық әдістер Н. г. Бруевич, В. А. Зиновьев, А. Г. Оваки - мов, П. А. Лебедев және т. б. еңбектерінде қолданылды. кеңістіктік механизмдердің позициялары туралы мәселе векторлардың проекцияларына өтпей-ақ векторлық түрде шешілген кезде тиімді тәсіл болып табылады [24] . 24] .
2. 1. Тікелей ережелер мәселесі
Сілтемелердің абсолютті позицияларын олардың берілген салыстырмалы позицияларымен анықтау мәселесі әртүрлі әдістермен шешіледі. Қатты дененің соңғы қақпасының формулаларын қолдануға негізделген әдіс. Бұл әдіс вектордың ескі орнын, айналу осі мен айналу бұрышын біле отырып, жаңа орнын анықтауға мүмкіндік береді. Қатты дененің соңғы айналуының әртүрлі формулаларын қарастырыңыз. Родригоның белгілі формуласы [16]
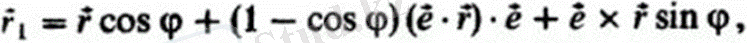
мұндағы r и r-бұрылуға дейін және кейін денемен байланысқан векторлар; è-бұрылу осінің орт; F-бұрылу бұрышы. Бұл формулаға ауыстыру арқылы басқа көрініс беруге болады
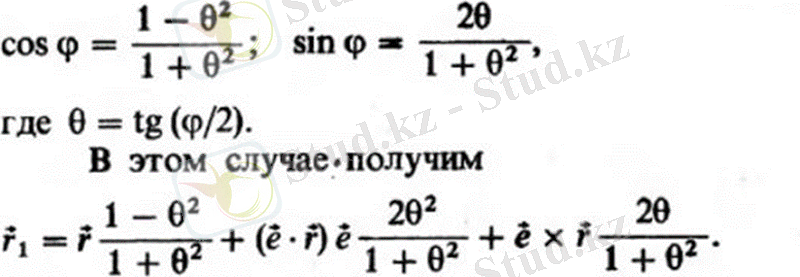
Егер ось мен Вектор арасындағы бұрыш т/2-ге тең болса, онда формула жеңілдетіліп, форманы алады
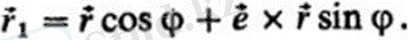
Е1 және е2 орталарымен анықталған осьтер айналасында дененің екі соңғы бұрылысын жасаған кезде, нәтижесінде пайда болатын ауыз формула бойынша болады

Соңғы формула тұрақты осьтердің айналасындағы қатты дененің екі соңғы бұрылысының нәтижесі осы бұрылыстардың орындалу тәртібіне байланысты екенін көрсетеді. Вектордың координаталарын түрлендірудің матрицалық әдісі. Үш декарттық координаттар жүйесін қарастырыңыз: Oxyz, 01x1y1z1 және O2x2y2z2. O2x2y2z2 жүйесінде вектордың координаталары берілсін (x2, y2, z2) . Содан кейін 01x1u121 жүйесінде сол вектордың координаталарын матрицалық түрде келесідей анықтауға болады: [x, ] = L2 [x2], (2. 2) бағанға вектордың кокрдинаты
мұндағы [x1] = [x1, у1, z1] - матрица-01x1v121 жүйесіндегі вектордың координаталық бағанасы; [x2] = [x2, y2, 22] - матрица-02х2у2z2 жүйесіндегі вектордың координаталық бағанасы, мұндағы "т" индексі матрицаны ауыстыру операциясын білдіреді;
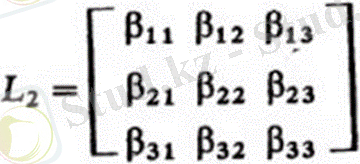
- O2x2y2z2 жүйесінен 01x1y122 жүйесіне өту матрицасы. L2 матрицасының by (i, j = 1, 2, 3) элементтері O2x2y2z2 жүйесінің осьтерінің бағыттаушы косинустары 01x1u121 жүйесінің осьтеріне қатысты. Сол сияқты, o1x1y1z1 жүйесінен oxyz жүйесіне координаталарды түрлендіру үшін [x] = L, [x, ], (2. 3) жазуға болады, мұнда [x] = [x, Y, z] - матрица-Oxyz жүйесіндегі вектордың координаттар бағаны;
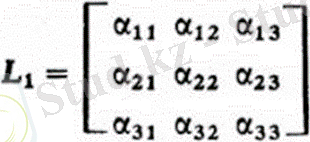
- O1x1y1z1 жүйесінен Oxyz жүйесіне өту матрицасы. L1 матрицасының элементтері (i, j = 1, 2, 3) Oxyz жүйесінің осьтеріне қатысты 01x1u121 жүйесінің осьтерінің бағыттаушы косинустары бар.
Өрнектерде (2. 3) [x1] өрнектен (2. 2) ауыстыру арқылы біз аламыз
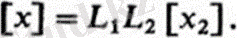
N координаттар жүйесі үшін жазуға болады
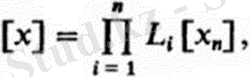
матрица-жүйеде вектордың координаттар бағаны
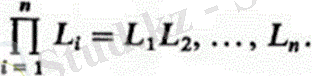
Мысал: манипулятордың абсолютті позицияларын векторлық әдіспен анықтау. Бес кинематикалық жұбы бар манипуляторды қарастырыңыз (сурет. 2. 1) . Біз кинематикалық жұптардағы байланыстардың салыстырмалы айналу бұрыштары қабылданған механизмнің жалпыланған координаттарын анықтаймыз. Мәселені шешу үшін біз манипуляторды барлық жалпыланған координаттар нөлге тең болатын "нөлдік" позицияға орнатамыз. Манипулятордың жағдайы кез - келген уақытта оның сілтемелер мен кинематикалық жұптардың осьтерінің бағдарымен және олардың жағдайымен анықталады. "Нөлдік" позицияда векторлар,
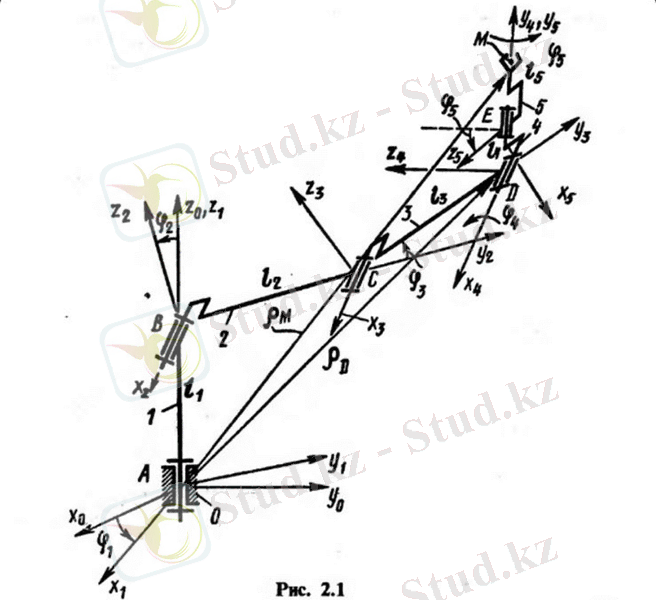
бағытталған осьтер бойынша звенолардың және кинематикалық жұп деп есептейміз белгілі. Манипуляторды "нөлдік" позициядан жалпыланған координаттар белгілеген позицияға ауыстыру үшін (і = 1, . . . , 5) біз бекітілген сілтемеден бастап F бұрыштарына тізбектелген бұрылыстар жасаймыз. Бұл жағдайда І2, із, і4, і5 векторлары өз позицияларын өзгертеді және векторларға өтеді () 1) (1) 1) Бұл векторларды Родриго формуласы бойынша табуға болады
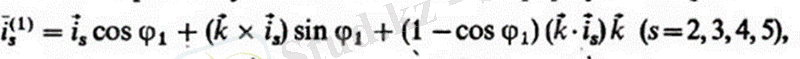
мұндағы i, j, k-декарттық координаттар жүйесінің бірлік векторлары (орталары) . I векторлары бір-бірімен коллинеарлы және К векторына ортогональды болғандықтан, соңғы формулада үш вектордан тұратын мүше нөлге тең; осыны ескере отырып, біз аламыз
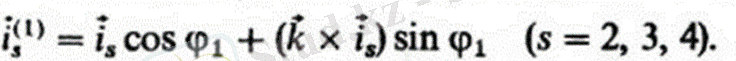
J2, j3, J4 векторлары өзгеріссіз қалады.
Екінші бұрылыс I2 векторының айналасындағы F4 бұрышына дейін жасалады) . Бұл жағдайда J2, j3, j4 векторлары бағытын өзгертеді, олар J2), 32), 32) векторларына өтеді, сонымен қатар
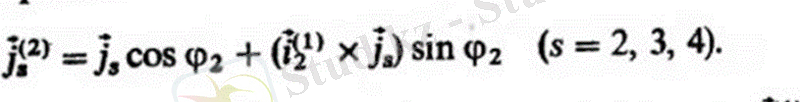
Осы формулада J2 өрнегін алмастыра отырып, біз аламыз
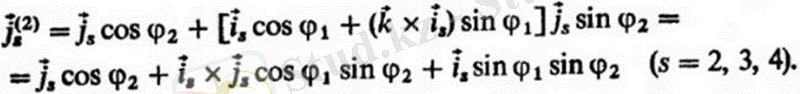
Бұл қозғалыста С және D жұптарының осьтерінің орны өзгермейді. Үшінші бұрылысты иа түйіспесінде жүзеге асырамыз 1) коллинеарлы вектордың векторының айналасында 4 5 сілтемелерімен байланысты векторлардың бағыты өзгереді. Бұрыштар мен параллель осьтердің айналасындағы екі бұрылыс бір бұрышқа (φ2 фз) тең екенін есте ұстаған жөн, сондықтан оны жазуға болады
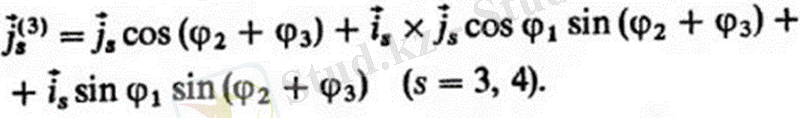
Төртінші бұрылыс В және С жұптарының осьтеріне параллель d жұбы осінің айналасында жүзеге асырылады; 83 векторымен анықталған Е жұбы осінің жаңа орнын анықтауға болады) .
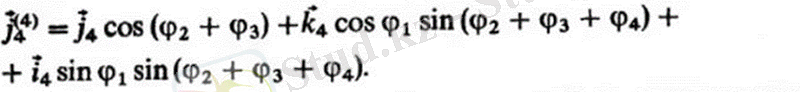
All Ciri бесінші бұрылыс E жұпында I векторының айналасындағы F5 бұрышына дейін жүзеге асырылады; бұл жағдайда осы сілтемемен байланысты is векторының орны анықталады
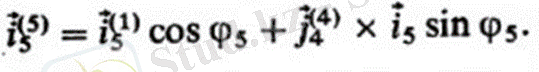
Жұптар мен сілтемелер осьтерінің позицияларын анықтайтын векторларды анықтағаннан кейін механизм нүктелерінің абсолютті позициялары оңай болады, мысалы:
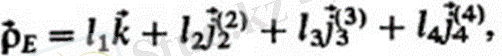
мұндағы-байланыстардың ұзындығы. Табылған векторлар кеңістіктегі манипулятордың абсолютті орнын толығымен анықтайды.
30-36 бет
(2. 25) өрнегінен біз JSX/j5y =j3x/j3y аламыз.
(2. 17) (2. 26) ауыстыру, біз аламыз
J5x - sin 1 cos($2 + F3) R jsy cos F1 cos (2 + 93) sin 91 cos F1 = -tg1.
(2. 18) сәйкес бізде jsx / jsy-XP / Ur бар.
Сонымен, orta проекцияларын анықтаған кезде, js және js бір-бірімен (2. 28) қатынаста болуын қамтамасыз ету керек. Бұл шартты, мысалы, объектіні көлденең жазықтыққа (20 осіне перпендикуляр жазықтық) орнату операциясы қанағаттандырады, осылайша uz осі көлденең жазықтыққа перпендикуляр болады (сурет. 2. 3) . Бұл жағдайда қозғалмайтын координаттар жүйесінің осіндегі is Ort проекциялары Usx jsy jsz болады] - [0, 0, -1] '.
Осылайша, суретте көрсетілген манипулятордың жалпыланған координаттарын анықтау үшін. 2. 1, келесі алгоритмді қолдануға болады:
(2. 7) формулалары бойынша D нүктесінің координаталарын анықтаймыз; (2. 11) формулалары бойынша ф1;
(2. 9) формуласы бойынша ф3 жалпыланған координатасының екі мәнін анықтаймыз; (2. 13) және (2. 14) формулалары бойынша екі мәнді анықтаймыз
берілген проекциялар бойынша (2. 19) - (2. 22) формулалар бойынша
ex, y, 25 координаттар жүйесінің орталары [(2. 25) шартын ескере отырып]
F4 және F3 жалпыланған координаттарының мәндері анықталады. Ұсынылған алгоритм есептеулердің үлкен көлемімен байланысты екені анық. Сондықтан, мұндай есептеулер үшін компьютерді пайдалану дұрыс емес.
Мысал ретінде ЭЕМ-де іске асырылған бағдарламаның көмегімен мынадай бастапқы деректер кезінде тор манипуляторының жалпыланған координаттары анықталды: объектінің координаттары: хм = 100 мм, ум = 150 ММ, ZM = 250 мм;
орта проекциялары is: isx = 1, isy = 0, 15x = 0; орта проекциялары js: jsx = 0, jsy = 0, jsx=-1; манипулятор буындарының ұзындығы: 1 = 200 мм, 12=200 мм,
13 = 200 мм, 14 = 50 мм, Is = 50 мм.
Есептеу нәтижесінде жалпыланған координаттардың келесі мәндерін аламыз (град)
-33, 690 -33, 690 93, 867108, 210 -75, 657 -33, 690
-33, 690
-14, 342
108, 210 176, 133
Алты айналмалы жұп манипулятордың позициясы туралы кері есеп. Манипулятор (сурет. 2. 4) ол бұрын қарастырылғаннан бағдарлы қозғалыс үшін тағы бір кинематикалық жұптың болуымен ерекшеленеді, ал қарастырылып отырған манипулятордың еркіндік дәрежелерінің саны алтыға тең. Мұндай құрылымның манипуляторы үшін позициялардың кері есебі алғаш рет жұмыста шешілді [33] ; векторлық координаталарды түрлендіру үшін матрицалық формулалары бар векторлық әдіс қолданылды.
Келесі шамалар белгілі: объектіге немесе ұстап алуға жататын М нүктесінің координаттары: хм, ақыл, ZM;
FX fx6y626, FX:
16x
16 i6y; 16
-162
J6x
J6y; K
k6x
к
II, 22 . 33, 44,
FS, FB, suene-дің он бір ережесін қосыңыз. PM, :: PM =1+1+1+14+1С+16
PE = PM - 1s-16 ;
ПЭ=1, +12 +13 + 1; Is = jols;
16 = jd6;
PE=PM - (ls + lo) j6.
2. (2. 35) мынадай:
XE = XM → (ls + lo) jox;
YE = Joy - (LS + lo) joyi
ZE=ZM - (ls + 16) j62.
11 11, 12, 13, 14 мынадай:
-12cos 2 жоқ 1 12 cos z cos 121 12 жоқ $2 -13 cos ($2 + 3) sino1 14 Жоқ (2 + 3)
-14 Қос (2+3),
I cos (22+3) cos 1
13 cos ($2 +33) cos 1; 13 жоқ (2 + 3)
E (2. 37) Sin (2. 32), e e: XE=0-12 COS 2 жоқ 1 - 13 COS (zz +33) жоқ + 1 -
-14 cos (2 + 3) 1 жоқ; yE=0 + 12 cos 2 cos p1 + 13 cos (zz + 3) cos 1 + + 14 cos (zz +33) cos11; ZE = 11 + 12 2 + 13 жоқ (22 + 3) + 14 жоқ (92 + 93) .
Түрлендіруден кейін біз аламыз:
XE = −[lz cos z + (3+ la) cos (z + 3) ] sin 1;
yE = [12 cos 2 + (13 + 14) cos (FZ + 3) ] cos 1; ZE=11 + 12 sin 2 + (13 + l4) sin (2 + 3) .
(2. 36), (2. 38) және жоғарыда баяндалған әдістемені пайдалана отырып,
f1, f2, f3 жалпыланған координаттарын F4, F3 жалпыланған координаттарын табу үшін табуға болады. фб, бағдарын анықтайтын, біз жазамыз
= cos FS
(2. 39
Орт 16 проекциялары белгілі (олар бастапқы деректерде берілген), орт вј3 проекциялары келесідей
-sin 1 cos (2 + 3) cos 1 cos (2 + 3) sin (2+3
(2. 40)
(2. 39) және (2. 40) мынадай: cos Q5 =-j6x sin 1 cos (F2 + 3) + j6y cos $1 cos($2 + F3) +
+ j6x sin (FZ + 3) ;
Q5 = + arccos [(6y cos 1 - 16x sin F1) cos (2 + 3) + + j6z sin (2 + 3) ] .
. (2. 42) FS жалпыланған координаты бірдей ұстау жағдайында (6-сілтеме) екі мәнді қабылдай алады.
13 және 16 орталардың векторлық көбейтіндісін қолдана отырып, орта is проекцияларын бөліңіз:
is =3 %) /sins. X
Пайдалана отырып, формула
sin s = tyi - cos2 us
және (2. 43), біз орта проекцияларын аламыз: (3x6z - I3zj6y) / ±V / 1-cos2 F5
U3zj6x-I3x6z) /+v1 - cos2 FS-03x6y-j3x6x) / +v1 - cos2 os
Ort is бірдей ұстау жағдайында екі қарама-қарсы болуы мүмкін
B
F5 бұрышының екі мәніне сәйкес
F4 бұрышын анықтау үшін өрнектерді қолданамыз
13. is = cos ф4;
i3 - is = sin Q4 .
Орта із проекциялары
cos F1 sin 91
0
i3 = 1% cos 1 + jo sin F1.
(2. 46)
(2. 47)
(2. 48)
(2. 49)
15x, 133 орта is проекцияларын (2. 40) және (2. 45) көмегімен келесі түрде жазуға болады:
[j6x cOS F1 cos (f2 + f3) - joy sin (f2 + f3) ] Vi-cos2 FS
[j6x sin (2 + F3) + Jor sin 10 cos ($2 + F3) ]
Vi-cos² us
[- 16y sin 1 cos (ф2 + ф3) - jox cos ф, соѕ (фа + ф3) ] .
Vi-cos2 FS
мұндағы k = +1. Бірі (2. 46) керек
COS Q4 = 13x15x + 13y15y + 13zisz.
Бірі - (2. 47) керек
sin F4 = +[(ізуі 5z-i3zisy) 2 +(13zisx-i3x15z ² 2 +
+(13xisy - i3, 5x) 2] 1/2.
k.
(2. 50)
(2. 51)
Радикал алдындағы белгі (2. 51) оң болады, егер из × is және орта з векторлық көбейтіндісінің проекцияларының белгілері сәйкес келсе, әйтпесе белгі теріс болады. I вектордың екі бағыты болуы мүмкін болғандықтан, F4 жалпыланған координатасы екі мәнді алады (is бағытына байланысты) . Алайда, талдау жалпыланған Ф4 координатасының осы екі мәні П мәніне бір-бірінен ерекшеленетінін көрсетеді, мысалы-N < 4 < +p, шектеулерді қою арқылы алынған мәндерді талдау арқылы қабылданған шектеулерді қанағаттандыратын ф4 мәнін таңдауға болады. Бұл жағдайда жалпыланған коор-фз және орта is бағыты нақты анықталады.
Егер FS жалпыланған координатасы F5 = 0 мәнін қабылдаса; FS = ±p, яғни sin s = 0 болған кезде, F4 және FB жалпыланған координаттарының мәндерін табу кезінде белгісіздік пайда болады, өйткені бұл жағдайда iz орталары параллель және F4 және FB жалпыланған координаттарын басқару бір-бірін қайталайды. Бұл жағдайда жалпыланған координат F4 = 0, Ort is параллель lelen ortu i3 және объектінің бағыты F6 жалпыланған координатасы деп санаймыз. жүзеге асырылады
FB бұрышын анықтау үшін is және 16 орталарының векторлық және скалярлық көбейтінділері үшін өрнектерді де қолданамыз:
is. 16 = cos 96 ;
is x is = sin 6 .
(2. 52)
(2. 53)
Орта 16 проекциялары белгілі. Орта is проекциялары бұрын анықталған [қараңыз (2. 50) ] . Бірі (2. 52) керек
cos 6 = isx16x + İsyi6y + iszi6z
Бірі (2. 53) керек
sin 6 = +[(isyi6z - İszi6y) 2 + (isz¹6x - i5x16z) 2 + + (İsxi6y - i5yi6z) 2] 1/2.
(2. 54)
(2. 55)
Егер is x 16 және orta 16 векторлық көбейтіндісінің проекцияларының белгілері сәйкес келсе, в (2. 55) радикалының алдындағы белгі оң болады, әйтпесе белгі оң болады. Is векторының екі бағыты болуы мүмкін болғандықтан, FB жалпыланған координаты екі мәнді қабылдай алады (is бағытына байланысты) .
Осылайша, барлық жалпыланған координаттар анықталады. Қарастырылып отырған манипулятор алты еркіндік дәрежесіне ие және объектіні кеңістікте дұрыс бағытта бағыттай алады. Сондықтан, бұл жағдайда объектінің ережесін немесе ұстап алуды орнатуға ешқандай шектеулер жоқ.
Суретте көрсетілген тор манипуляторының жалпыланған координаттарын анықтау алгоритмі. 2. 4. мынадай: (2. 36) формулалар бойынша Е нүктесінің координаталарын анықтаймыз;
(2. 11) ұқсас формулалар бойынша біз мәнді анықтаймыз
жалпыланған координаталар ф1; (2. 9) ұқсас формула бойынша жалпыланған координаталардың екі мәнін анықтаймыз ф3;
(2. 13), (2. 14) ұқсас формулалар бойынша Ф2 жалпыланған координатаның екі мәнін анықтаймыз; (2. 42) -(2. 51) формулалар бойынша мүмкін болатын мәндерді анықтаймыз
жалпыланған координаттар Ф4 және фѕ және
F4 шектеулерінде біз қажетті F4 және FS мәндерін таңдаймыз; (2. 54), (2. 55) формулаларын қолдана отырып, FB жалпыланған координатасының мәндерін анықтаймыз. Қарастырылып отырған жалпыланған координаталарды есептеу үшін
манипуляторды қолдануға болады бағдарлама
предложение іске асыратын алгоритмдік тілде
әйел алгоритмі.
Мысал ретінде манипулятордың жалпыланған координаттарын келесі бастапқы деректермен анықтаймыз: объектінің координаттары: хм = 100 мм, ум = 150 мм, Zм = = 250 мм;
проекциялар орта 16: 16x = 1, 16y = 0, 16x = 0;
проекциялар орта16: 6х = 0, 16y = 1, j63 = 0; манипулятор буындарының ұзындығы: 11 = 200 мм, 12 = 200 мм, 13 = 150 мм, 14 = 150 мм, 15 = 50 мм, 16 = 50 мм. есептеу нәтижесінде біз жалпыланған координаттардың келесі мәндерін аламыз (град) :
111, 478 73, 981 144, 957
85, 853
-63, 435
-111, 502
163, 402
-63, 435 159, 692 163, 402 -88, 146 63, 495
Вектордың соңғы бұрылысының (2. 1) формуласын кері есептерді шешуде, төменгі жүннің айнымалы және тұрақты параметрлері арасында байланыс орнату үшін қолдануға болады
Бұл әдіс [53] жұмысында қолданылады, онда алты айналмалы жұптары бар манипулятордың позициялары туралы кері есепті шешудің тиімді алгоритмі жасалынған, ол күріш сияқты бірдей схемаға ие. 2. 4. Алгоритмнің ерекшелігі-вектордың соңғы бұрылысының қашырларын дәйекті пайдалану.
Тұтқындаудың жалпыланған координаттары белгілі: Эйлер +, ф, 0 бұрыштары және кейбір нүктелердің координаттары С: хо yo> 20. F: (i = 1, ) буындарының салыстырмалы айналу бұрыштары анықтауға жатады . . . , 6) .
Оң жақ координаттар жүйелері манипулятордың сілтемелерімен байланысады: So, S1, . . . , S6, осьтері 2; (i = 0, 1, . . . , 6) айналмалы жұптардың осьтері бойымен бағытталған (сурет. 2. 5) . Табиғат нүктелері, сынған бұрыштардың нүктелері О, А, В, С деп белгіленген.
37-43 беттер аудармасы
Мәселені шешу үшін келесі порттар қолданылады:
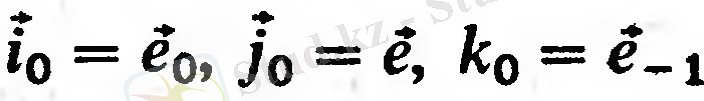 - орт жүйесі
- орт жүйесі
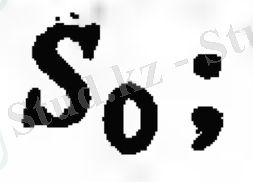
 - орт жүйесі
- орт жүйесі
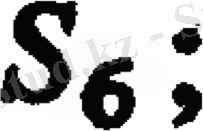
 -осьтің проекциясы
-осьтің проекциясы
 жазықтыққа
жазықтыққа
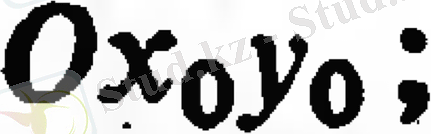
 -орт, жазықтық
-орт, жазықтық
 және векторға перпендикуляр
және векторға перпендикуляр

 - арасындағы бұрыштар
- арасындағы бұрыштар
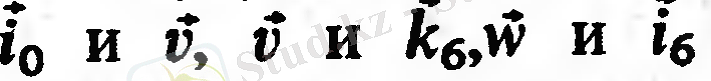 -бірінші өнерден екіншісіне есептеледі, егер сіз сәйкесінше
-бірінші өнерден екіншісіне есептеледі, егер сіз сәйкесінше
 ұштарынан қарасаңыз.
ұштарынан қарасаңыз.
 бұрыштары
бұрыштары
 жүйесіне қатысты
жүйесіне қатысты
 жүйесінің бағытын анықтайды.
жүйесінің бағытын анықтайды.
Параметрлер арасындағы байланыс теңдеулері
 арқылы жазылған
арқылы жазылған
 . . . , өрнектерді теңестіру жағдайынан алынады
. . . , өрнектерді теңестіру жағдайынан алынады
 .
.
 бұрыштарының функциясында
бұрыштарының функциясында
 өрнектерін құрастыру үшін (2. 1) қатынасы қолданылады.
өрнектерін құрастыру үшін (2. 1) қатынасы қолданылады.
Бұл мәселені шешу алгоритмі [54] :
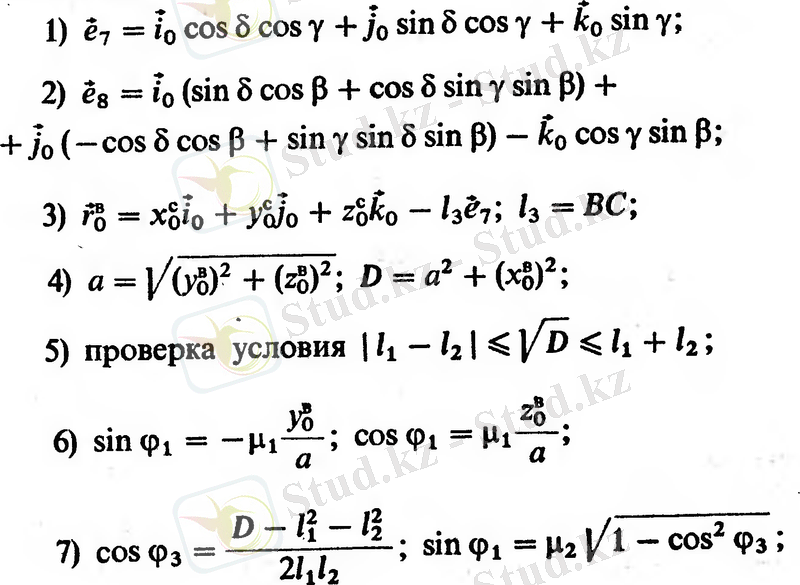
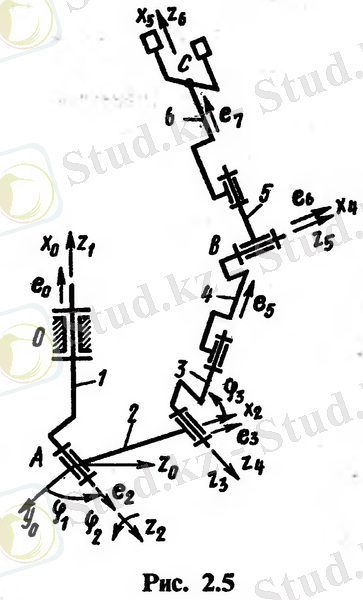
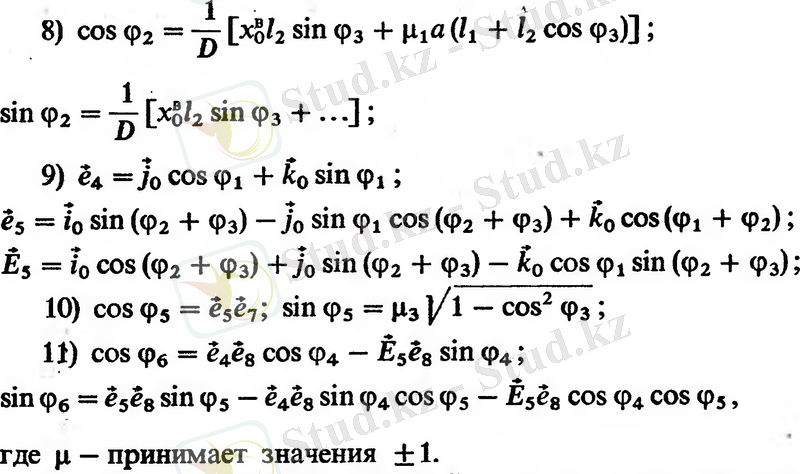
Алынған өрнектерді талдау тек екі шешім айтарлықтай ерекшеленетінін көрсетеді.
Бес айналмалы және бір аударма жұбы бар манипулятордың позициялары туралы есеп (сурет. 2. 6) .
Суретте көрсетілгендей координаттар жүйесін манипулятордың сілтемелерімен байланыстырамыз.
 -сілтеменің орны берілген. Бұл жағдайда F нүктесінің координаттары және
-сілтеменің орны берілген. Бұл жағдайда F нүктесінің координаттары және
 жұп осінің орт-ы белгілі.
жұп осінің орт-ы белгілі.
Е нүктесінің координаттарын анықтаймыз.
Векторлық қосындыны жазуға болады
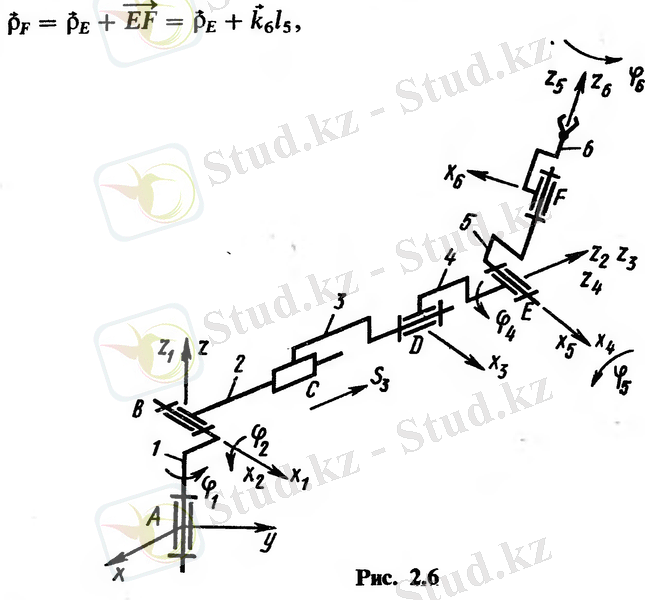
мұндағы
 F и E нүктелерінің радиус-векторы
F и E нүктелерінің радиус-векторы
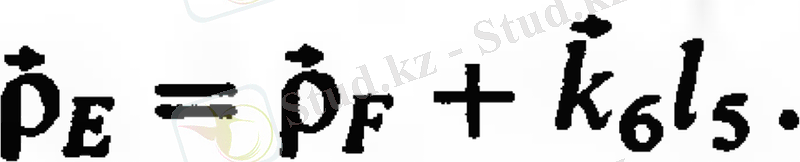
Вектордың
 проекциясы немесе Е нүктесінің координаталары, қозғалмайтын координаттар жүйесінде тең
проекциясы немесе Е нүктесінің координаталары, қозғалмайтын координаттар жүйесінде тең
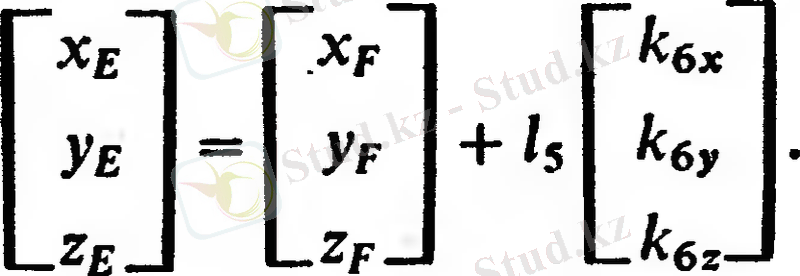
B, D және E осьтерінің орталары (
 векторлары) үш сұрыпты формуланы қолдана отырып анықталады (I-қосымшаны қараңыз)
векторлары) үш сұрыпты формуланы қолдана отырып анықталады (I-қосымшаны қараңыз)
 анықтаңыз. Бізде
анықтаңыз. Бізде
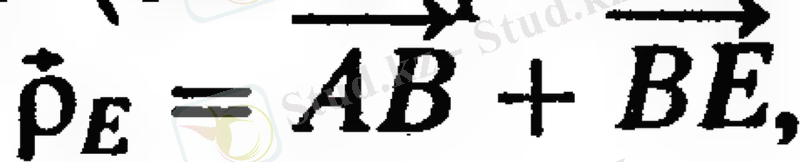 , қайдан
, қайдан
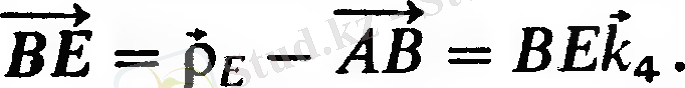
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz