ЭЛЕКТРОСТАТИКАЛЫҚ ӨРІСТЕГІ ӨТКІЗГІШТЕР

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

№3 Лекция. ЭЛЕКТРОСТАТИКАЛЫҚ ӨРІСТЕГІ ӨТКІЗГІШТЕР

Жоспар

1. Зарядтардың өткізгіште орналасуы.

2. Өткізгіштің бетіндегі электр өрісі және оның зарядтардың беттік тығыздығымен байланысы. Әсерлесу арқылы электрлену. Электростатикалық қорғау

3. Өткізгіштердің электр сыйымдылығы

Зарядтардың өткізгіште орналасуы. Өткізгіштің бетіндегі электр өрісі және оның зарядтардың беттік тығыздығымен байланысы. Әсерлесу арқылы электрлену. Электростатикалық қорғау . Егер электростатикалық өріске бір өткізгішті ендірсек немесе өткізгішке аздаған заряд берсек, онда электрлік күштердің әсерінен осы зарядтар орын ауыстыра бастайды. Сөйтіп зарядтар тепе-тең болып бөлінгенге дейін, өткізгіштер қозғалыста болады. Осы кезде өткізгіш ішінің барлық жеріндегі өріс кернеулігі нөлге тең болады 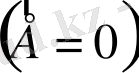, себебі, өткізгіш ішіндегі потенциалдар тұрақты болу керек. Сонымен қатар өткізгіш бетінің әрбір нүктесіндегі epic кернеулігі бетке нормаль бойымен бағытталады. Демек, тепе-тендік жағдайда өткізгіштің беті эквипотенциал болады. Тепе-теңдік кезінде өткізгіш ішіндегі кез келген нүктеде өріс болмағандықтан, бет арқылы электрлік зарядтардың ығысу векторының ағыны нөлге тең болады. Ол зарядтардың алгебралық қосындысы да Остроградский-Гаусс теореясына сәйкес нөлге тең. Олай болса, тепе-теңдік кезінде өткізгіш ішіндегі ешбір жерде артық заряд болуы мүмкін емес, сөйтіп зарядтар өткізгіштің бетінде белгілі бір тығыздықпен (σ) орналасуы керек. Жалпы өткізгіштің берілген потенциалында зарядтардың тығыздығы беттің қисықтығымен анықталады. Ол қисықтың оң болғанда (дөңес) тығыздық артады да, теріс болғанда (ойыс) кемиді. Зарядтардың тығыздығы, әсіресе сүйір ұштарда көп болады.

Зарядталмаған өткізгішті электр өрісіне енгізгенде заряд тасушылар қозғалысқа келе бастап, оң зарядтар вектордың бағытымен, ал теріс зарядтар қарама-қарсы бағытта қозғала бастайды. Осының нәтижесінде өткізгіштің ұштарында индукцияланған зарядтар деп аталатын қарама-қарсы таңбалы зарядтар пайда болады. Сөйтіп индукцияланған зарядтар өткізгіштің сыртқы бетіне бөлініп таралады. Егер өткізгіштің іші қуыс болса, онда индукцияланған зарядтардың тепе-теңдігі кезінде оның ішіндегі өріс нөлге тең болады. Сондықтан да денедегі сүйір ұштың болуы одан зарядтың кетуін ғана туғызып қоймай, сондай-ақ басқа денелерден өткізгішке зарядтардың ағып келуін туғызады.

Егер өткізгішке бір 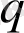заряды берілсе, онда ол өткізгіштің ішіндегі өріс кернеулігі 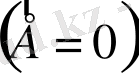болатындай таралады. Сондай-ақ өткізгіштегі зарядтың артуы қоршаған денелердегі зарядтардың бөлініп таралуына өзгеріс туғызбаған жағдайда ғана орындалады. Сөйтіп, шамалары әр түрлі зарядтар басқа денелерден оңашаланған өткізгіште осы тәртіппен тарайды. Сонда өткізгіш бетінің кез келген екі нүктесіндегі заряд тығыздықтарының қатынасы зарядтың кез келген шамасы үшін бірдей болады. Бұдан оқшауланған өткізгіштің потенциялы ондағы бар зарядқа пропорционал болатынын көруге болады. Мысалы, өткізгіштегі зарядты қанша есе арттырсақ, онда өрістің әрбір нүктесіндегі кернеулігінің де сонша есеге артатынын байқаймыз. Олай болса, бірлік зарядты шексіздіктен өткізгіштің бетіне алып келу үшін істелген жұмыс және оның потенциялы еселеп артады. Сонымен, оқшауланған өткізгіш үшін:

(1)

мұндағы пропорционалдық коэфициент С өткізгіштердің электр сыйымдылығы деп аталады, ол

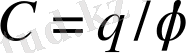(2)

Сонымен, сыйымдылық сан жағынан өткізгіштің потенциалын бір өлшемге арттыруға қажетті зарядқа тең екен.

Өткізгіштің сыйымдылығы оның пішіні мен өлшеміне тәуелді де бірақ өткізгіштің тегіне тәуелсіз. Мұны зарядтардың көпшілігі негізінен өткізгіштің сыртқы беттеріне орналасуынан деп түсінуге болады. Сыйымдылықтың өлшем бірлігіне өткізгішке 1Кл-ға тең заряд бергенде оның потенциялы 1В-ке өзгеретін өткізгіштің сыйымдылығы алынады. Сыйымдылықтың бұл өлшемі фарада (Ф) деп аталады.

Енді радиус оқшауланған шардың сыйымдылығын анықтайық. Ол үшін шар диэлектрлік өтімділігі біртекті өрісті болсын, сонда оның потенциалы:

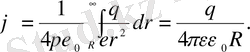(3)

Осы өрнекті (2) формулаға қойып, шардың сыйымдылығын табайық:

(4)

Сонда шардың радиусы 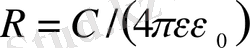болар еді немесе м. Ал бұл шама Жердің радиусынан 1500 есе үлкен өлшеммен сыйымдылықты өлшеу мүмкін емес. Сондықтан практикада оның үлестеріне тең мынадай өлшемдер қолданылады: (микрофарад) 1мкФ 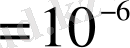Ф, (нанофарад) 1нФ 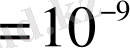Ф, (пикофарад) 1пФ 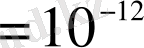Ф және т. б. өлшемдер.

№6 Лекция. ДИЭЛЕКТРИКТЕРДЕГІ ЭЛЕКТР ӨРІСІ

Жоспар

Диэлектриктердегі өрісті сипаттаушы Остраградский-Гаусс теоремасы
Сегнетоэлектриктер. Пъезоэлектриктер. Электреттер

Жоғарыда көрініп тұрғандай электростатикалық өріс ортаның қасиеттеріне байланысты болады. 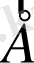векторы диэлектриктердің шекарасынан өткенде секірмелі түрде өзгеріске ұшырайды. Бұл электростатикалық өрісті есептеулерде қолайсыздықтар тудырады. Сондықтанда электр өрісін сипаттау үшін кернеулік векторымен қоса электрлік индукция векторыда қажет болады.

Біртекті электрлік орта үшін анықтамаға сәйкес ол мынаған тең:

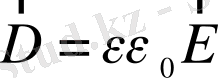, (5)

мұндағы 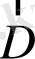- электрлік индукция векторы деп аталады. Поляризация векторының өрнегін қолдансақ, соңғы өрнек былай жазылады:

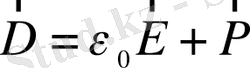(6)

Байланысқан зарядтардың еркін электрондардан айырмашылығы, олар құрамына кіретін молекуланың шегін тастап кете алмайды. Қалған жағынан олардың барлық қасиеттері барлық басқа зарядтардікі сияқты, яғни өрістің векторлық сызықтары әрі еркін, әрі байланысқан зарядтардан басталып және аяқталуы мүмкін . Ал электрлік индукция векторы 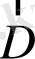болса, тек еркін зарядтардан ғана басталып аяқталады.

Сондықтан тұйықталған бет үшін электрлік индукция векторын есептеуде Остроградский-Гаусс теоремасын мына түрде

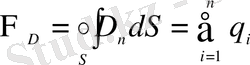(7)

жазып қолданамыз.

Тұйықталған бет арқылы электрлік ығысудың векторлық ағыны осы беттің ішіндегі еркін зарядтардың алгебралық қосындысына тең.

Енді тұйықталған бет үшін өрістің кернеулік вектор ағынын есептегенде тек еркін зарядтардың ғана емес, осы беттің ішіндегі байланысқан зарядтардың да алгебралық қосындысын есептеу керек. Сондықтан векторы үшін Остроградский-Гаусс теоремасын мына түрде жазайық:

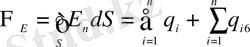(8)

мұндағы 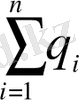және 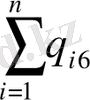- тұйықталған бет қамтитын еркін және байланысқан зарядтардың алгебралық қосындысы.

Соңғы (8) теңдеу арқылы диэлектриктегі 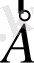векторды тікелей табу қиын, сондықтан бұл қиындықтан 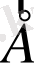векторымен қарапайым түрде байланыста болатын (6) қатынасын және кеңістіктегі еркін зарядтардың таралуымен анықталатын (7) формуланы пайдалану арқылы құтылуға болады.

Сегнетоэлектриктер. Диэлектриктердің сыртқы электр өрісі болмағанда өздігінен (спонтанды) белгілі бір температуралар аралығында поляризациялана алатын тобын сегнетоэлектриктер деп атаймыз. Бұл құбылысты алғаш рет сегнет тұзының (шарап қышқылының қос калий-натрий тұзы KNaC ₄ H ₄ O ₆ ·4H ₂ O) электрлік қасиеттерін егжей-тегжейлі зерттеген (1930-1934 жылдары) совет физиктері И. В. Курчатов (1930-1960) және И. П. Кобеко болды.

Сегнетоэлектриктердің поляризациялану тәртібі ферромагнетиктердің магниттелу тәртібіне ұқсас, сондықтан да сегнетоэлектриктер кейде ферроэлектриктер деп аталады.

Кристалды заттар оның ішіндегі симметрия центрі жоқтары ғана сегнетоэлектриктер бола алады. Сегнетоэлектрик кристалдағы бөлшектердің өзара әсерлері олардың дипольдік моменттерін өздігінен бір-біріне параллель орналасатындай қалыпқа келтіреді. Кейде дипольдік моменттердің бірдей бағдарлануы кристалға түгелдей таралады, бірақ кристалдың қорытқы моменті нөлге тең болады.

Өздігінен поляризациялану аймақтары домендер деп аталады. Сыртқы өрістің әсерінен домендердің моменттері біртұтас өріс бағыты бойынша бұрылады.

Дененің сегнетоэлектрлік қасиеті оның температурасына байланысты. Жоғары температурада дененің сегнетоэлектрлік қасиеті төмендеп, кәдімгі диэлектрикке айналады. Сондықтан температураның бұл нүктесін Кюри нүктесі (Л. Кюри I859-I906) деп атайды. Сегнет тұзының екі Кюри нүктесі бар (-18ºС және +24ºС) .

Совет физигі Б. М. Вул (1903-1985) барийлі титанның (ВаТіО 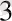) сегнетоэлектрлік қасиетін ашып, оның Кюри нүктесі 125ºС, ε =6000 екенін тапты. Бұл күрделі қорытпаның практикалық маңызы өте зор. Кюри нүктесіне жақындағанда сегнетоэлектриктердің жылу сыйымдылықтарының ( С ) кенеттен өсетіндігі байқалды. Сол сияқты сегнетоэлектриктердің жоғарғы температураларда, яғни Кюри нүктесінде кәдімгі диэлектрикке айналу екінші текті фазалық ауысуымен байқалады.