Параметрі бар теңсіздіктер: теориясы, шешу әдістері және қолданылуы


Кіріспе
Мен осы тақырыпты мектеп алгебра курсында өтілетін негізгі тақырыптардың бірі болғандықтан таңдадым. Осы жұмысты дайындау барысында, мен есепті шешеудің ең ұтымды әдісін табуды, осы тақырыпты тереңірек зерттеуді мақсат етіп қойдым.
Қазіргі өмірде көптеген физикалық процестер мен геометриялық заңдылықтарды зерттеу кезінде көбінесе парамері бар есептер көп қолданылады. Параметрлері бар есептер таза математикалық қызығушылық тудырады, оқушылардың интеллектуалды дамуына ықпал етеді және дағдыларды машықтандыру үшін жақсы материал болып табылады. Параметрі бар есептердің диагностикалық маңызы бар, өйткені олар математиканың негізгі бөлімдері туралы білімді, математикалық және логикалық ойлау деңгейін, алғашқы зерттеу дағдыларын және жоғары оқу орындарында математика курсын ойдағыдай игерудің перспективалық мүмкіндіктерін тексеру үшін қолдануға болады. Менің жұмысымда теңсіздіктердің жалпы түрлері қарастырылады және жұмыс барысында алған білімім мектеп емтихандарын тапсыру кезінде маған көмектеседі деп үміттенемін, өйткені параметрлері бар теңдеулер мектеп математикасы курсында өте қиын есептердің бірі болып саналады.
Мақсаты: Параметрі бар теңсіздіктерді шешудің ең ұтымды әдісін табу.
Міндеті:
- параметрлермен есептер шығару әдістерінің теориясын қарастыру,
- мысалдар келтіре отырып, параметрлермен есептер шығару әдістерін кезең-кезеңімен талдау;
- зерттелген материал негізінде қорытынды жасау.
Зерттеу нысаны: параметрлері бар теңсіздіктер.
Зерттеу әдістері:
• Эмпирикалық: проблема, гипотеза, тапсырмаларды қалыптастыру, жұмыс жоспарын құру, зерттеу жұмысының нәтижелерін рәсімдеу.
• Теориялық: әдеби және архивтік деректерді талдау.
- Параметрі бар теңсіздіктердің шығу тарихы
Параметрі бар есептер үнді математигі және астрономы Ариабхатаның 499 жылы құрастырған «Ариабхатиам» атты астрономиялық трактатында кездескен. Тағы бір үнді ғалымы Брахмагупта (VII ғ. ) канондық түрге келтірілген квадрат теңдеулерді шешудің жалпы ережесін көрсетті:
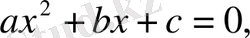

Мұхаммед әл-Хорезмидің алгебралық трактатында a параметрімен сызықтық және квадрат теңдеулердің жіктелуі келтірілген. Автор теңдеулердің 6 түрін санап, оларды былай өрнектейді:
1) «квадраттар түбірлерге тең», яғни
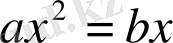 .
.
2) “Квадраттар санға тең”, яғни
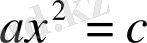 .
.
3) «Түбірлер санға тең», яғни
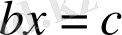 .
.
4) “квадраттар мен сандар түбірге тең”, яғни
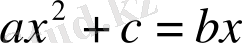 .
.
5) «Квадраттар мен түбірлер санға тең», яғни .
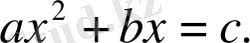
6) «Түбірлер мен сандар квадраттарға тең», яғни
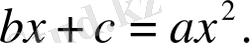
Еуропада әл-Хорезми бойынша квадрат теңдеулерді шешудің формулалары алғаш рет 1202 жылы итальяндық математик Леонардо Фиббоначчи жазған «Абак кітабында» ұсынылды. [1, 182 б. ] .
-ның әртүрлі таңбаларының комбиницияларында
Қазіргі кезде қолданылатын теңсіздік белгісін Рекордтың теңдік белгісінен кейін ағылшын ғалым Барриот енгізді. Жаңа белгіні ол былай түсіндірді: «егер екі шама тең болмаса, онда теңдік белгісінде қолданылған кесінділер параллель емес олар қиылысады» . Қиылысу оң жақтан да (>), сол жақтан да (<) болуы мүмкін. Бірінші жағдайдағы теңсіздік таңбасы «үлкен», ал екінші жағдайда «кіші» екенін білдіреді.
 Параметр туралы түсінік
Параметр туралы түсінік
Мектеп математика бағдарламасында параметрге қатысты есептер көп қарастырылмайтыны белгілі. Сондықтан, ең алдымен, мектеп математикасында параметр туралы идеяның өзі қатысатын тақырыптарды қаарстырайық. Параметр кейбір анықтамаларды беру кезінде қолданылады.
Мысалы;
- Сызықты функция:(x, y -айнымалылар, b-параметр)
- Сызықты теңдеу:(x -айнымалы, a, b-параметрлер)
- Квадраттық теңдеу:(x -айнымалы, a, b, с-параметрлер)
Мектеп курсында қарастырылған параметрлері бар тапсырмалар, мысалы, сызықтық және квадрат теңдеулер және теңсіздіктердің шешімдерін іздеу, түбірлер санын табу параметр мәндеріне байланысты зерттеледі.
Параметр - мәні белгіленген, тұрақты болатын тәуелсіз айнымалы.
Параметрі бар теңсіздік - теңсіздік пен оның шешімі бір немесе бірнеше параметрлердің мәндеріне байланысты болатын математиткалық теңсіздік.
Параметр (грек. parametron- өлшенетін) - кейбір жиын элементтерін бір-бірінен ажырату үшін қолданылатын шама. Мысалы, Декарттық координаталар жүйесінде xOy жазықтығындағы радиусы 1-ге тең барлық шеңберлер жиыны
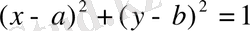 теңдеуімен анықталады; мұндағы
a=
5
, b=
4 десек, онда шеңберлер жиынынан центрі (3, 4) нүктесінде орналасқан шеңберді бөліп алуға болады, сондықтан
a, b
қарастырылып отырған жиындағы шеңбердің параметрлері.
теңдеуімен анықталады; мұндағы
a=
5
, b=
4 десек, онда шеңберлер жиынынан центрі (3, 4) нүктесінде орналасқан шеңберді бөліп алуға болады, сондықтан
a, b
қарастырылып отырған жиындағы шеңбердің параметрлері.
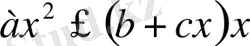 теңсізідігін қарастырайық. Берілген өрнек 4 әріптен тұрады:
a
,
b
,
c
,
x
. Біз бұл теңдеуді
x
айнымалысы бар теңсіздік ретінде, ал
a
,
b
,
c
әріптерін параметр ретінде қарастырамыз.
теңсізідігін қарастырайық. Берілген өрнек 4 әріптен тұрады:
a
,
b
,
c
,
x
. Біз бұл теңдеуді
x
айнымалысы бар теңсіздік ретінде, ал
a
,
b
,
c
әріптерін параметр ретінде қарастырамыз.
А- a шамасының барлық рұқсат етілген мәндердің жиынтығы, K- k шамасының барлық рұқсат етілген мәндердің жиынтығы, ал Х- х шамасының барлық рұқсат етілген мәндердің жиынтығы, C- c шамасының барлық рұқсат етілген мәндердің жиынтығы болсын. Егер A, K, C, X жиындарының әрқайсысында сәйкесінше α, k, c бір мәнін таңдап, оларды теңсіздікке алып қойсақ, онда біз х -ге қатысты теңсіздікті аламыз, яғни бір белгісіз айнымалысы бар теңсіздік. Теңсізідікті шешкен кезде тұрақты деп саналатын α, k, c айнымалылары параметрлер деп аталады, ал теңсіздіктің өзі параметрлері бар теңсіздік деп аталады.
Дәстүр бойынша, белгісіз айнымалыларды латын әріптерінің соңғы әріптерімен - х, у, z, ал параметрлерді бірінші латын әріптерімен- а, b, с немесе басқа алфавиттің әріптерімен (мысалы, грек) белгіленеді. Параметрі бар есепті шешу - бұл барлық сол және сол - есептің шешімі бар болатын параметрлердің мәндерін табу. Параметрлер нақты мәндерді ғана қабыладайды.
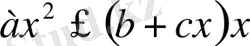 - параметрі бар теңсіздік, ал
х-
тәуелсіз айнымалы,
a
,
b
,
c - параметрлер.
- параметрі бар теңсіздік, ал
х-
тәуелсіз айнымалы,
a
,
b
,
c - параметрлер.
Берілген теңсіздіктің шешімі бар болатын
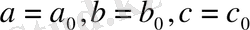 айнымалы мәндер жүйесі
параметрлердің рұқсат етілген мәндер жүйесі
деп аталады.
айнымалы мәндер жүйесі
параметрлердің рұқсат етілген мәндер жүйесі
деп аталады.
Мысалы;
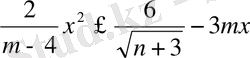 теңсіздігінде
m
және
n
параметрлердің рұқсат етілген мәндер жүйесі
теңсіздігінде
m
және
n
параметрлердің рұқсат етілген мәндер жүйесі
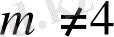 ,
n
>-3. Сонымен қоса,
,
n
>-3. Сонымен қоса,
 және
және
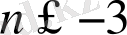 болғанда теңсіздіктің шешімі болмайды.
болғанда теңсіздіктің шешімі болмайды.
Параметрі бар екі теңсіздік эквивалентті деп аталады, егер
- олардың параметрлерінің рұқсат етілген мәндер жүйесі бірдей болса;
- бірдей шешімге ие болса.
Мысалы;
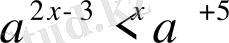 және
және
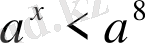 теңсіздіктер эквивалентті. Екі теңсіздік үшін де
теңсіздіктер эквивалентті. Екі теңсіздік үшін де
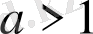 ,
,
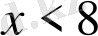 , және
, және
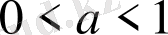 ,
,
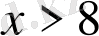 шешімдерін аламыз.
шешімдерін аламыз.
Параметрі бар теңсіздіктерді шешу үшін:
- параметрдің қандай мәнінде теңдеудің немесе теңсіздіктің шешімі болатынын анықтау керек;
- параметрдің әрбір мүмкін болатын мәндер жүйесі үшін сәйкес шешімдер жиынын табу қажет.
Егер теңсіздіктегі параметрге белгілі бір мән берілсе, онда келесі екі жағдайдың біреуі мүмкін:
1) тек сандар мен белгісіз айнымалылар қатысатын теңсіздікті аламыз;
2) мағынасы жоқ шартты аламыз.
Бірінші жағдайда параметр мәні қолайлы, екіншісінде қолайсыз деп саналады.
Параметрлердің кейбір мәндерінде теңдеудің түбірі жоқ немесе тек бір түбір, бірнеше түбір болады.
Мұндай теңсіздіктерді шешу кезінде:
1) параметрлердің рұқсат етілген мәндер жүйесін табу;
2) белгісіз айнымалысы бар барлық мүшелерді теңсіздіктің сол жағына, ал белгісізі жоқ барлық мүшелерді оңға жылжыту;
3) ұқсас мүшелерді біріктіру;
4) алынған теңсіздікті шешу.
Параметрі бар сызықты және сызықтыға келтірілетін теңсіздіктер
Келесі түрдегі теңсіздіктер
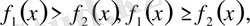
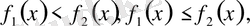
мұндағы
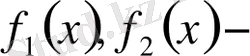 айнымалысы бар сызықты фунциялар, ал теңсіздіктер бір айнымалысы бар теңсіздіктер деп аталады.
айнымалысы бар сызықты фунциялар, ал теңсіздіктер бір айнымалысы бар теңсіздіктер деп аталады.
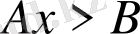 түріндегі теңсіздіктер (немесе
түріндегі теңсіздіктер (немесе
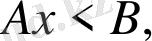
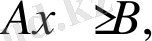
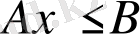 ) бір айнымалысы бар сызықты теңсіздік деп аталады. Мұндағы А және В -нақты сандар, ал х - белгісіз айнымалы.
) бір айнымалысы бар сызықты теңсіздік деп аталады. Мұндағы А және В -нақты сандар, ал х - белгісіз айнымалы.
- мәндес, яғни теңсіздіктің шешімдер жиыныаралығы.
- мәндес, яғни теңсіздіктің шешімдер жиыныаралығы.
- Егерондаүшін теңсіздіктің кез келгенүшін шешімі жоқ, алүшін теңсіздік кез келгенүшін орындалады.
Келесі түрдегі теңсіздік
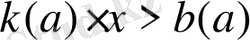 (1)
(1)
бір белгісіз айнымалысы мен параметрі бар сызықты теңсіздік деп аталады.
Кесте-2
- түріндегі параметрі бар сызықты теңсіздікті шешу алгоритмі:
 параметрінің рұқсат етілген мәндер жүйесі
параметрінің рұқсат етілген мәндер жүйесі
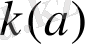 мағынасы жоқ
мағынасы жоқ
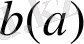 мағынасы жоқ
мағынасы жоқ
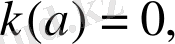
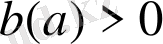
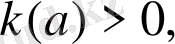
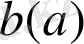 мағынасы бар
мағынасы бар
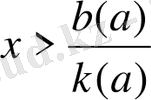
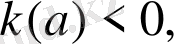
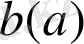 мағынасы бар
мағынасы бар
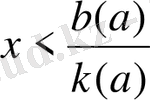
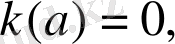
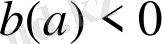
 кез келген сан
кез келген сан
Мысалы,
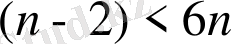 - параметрі бар сызықты теңсіздік.
- параметрі бар сызықты теңсіздік.
n= 2 кезінде ол келесідей түрде болады:
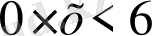
демек кез келген нақты x мәніне қатысты болады.
n>
2 кезінде
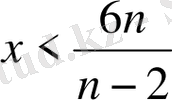 , ал
n<
2 кезінде
, ал
n<
2 кезінде
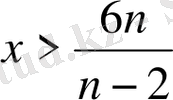 .
.
- Мысал:x-ке қатысты келесі теңсіздікті шешу:
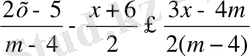 (2)
(2)
Шешімі :
m= 4 кезінде теңсіздіктің шешімі жоқ.
m> 4 кезінде, (2) теңсіздігі келесі теңсіздікке пара-пар
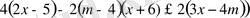
немесе
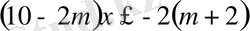 (3)
(3)
Осыдан,
m>
5 болғанда
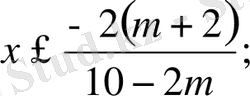
4
<m<
5 болғанда
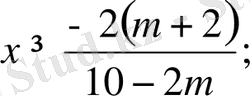
m=
5 кезінде (3) теңсіздігі келесі түрде болады:
 , демек
х-
кез келген сан.
, демек
х-
кез келген сан.
m< 4 кезінде, (2) теңсіздігі келесі теңсіздікке пара-пар
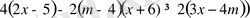
немесе
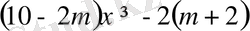
Осыдан,
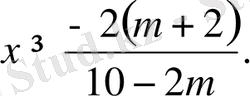
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz