Stud.kz

Информатикадан практикалық жұмыстар


Жұмыс түрі:  Материал
Тегін:  Антиплагиат
Көлемі: 24 бет
Таңдаулыға:   

Мазмұны

Практикалық жұмыс №1: Санау жүйелері2

Практикалық жұмыс №2: Логикалық жүйелер8

Практикалық жұмыс №3: Жүйелік блогқа құрылғының қосылуы және жүйелік блог компонеттерін меңгеру. 15

Практикалық жұмыс №4: Аналық платаның компонеттерін меңгеру. 19

Практикалық жұмыс №5: Компьютерді іске қосу тәртібін зерттеу21

Практикалық жұмыс №6: SETUP программасының компьютерлік жүйелерінің құрылғылары. 23

Лабораторная работа 7: Установка и удаление оборудования в ОС WindowsXP (Vista) 25

Практикалық жұмыс №8: Локалды жүйеге қосылу. Желілік картаны құру және баптаулары . . . 31 Практикалық жұмыс №1: Санау жүйелері.

Мақсаты: Сандардың әр-түрлі санау жүйелеріндегі көрінісін, оларды өзгерту әдістерін және негізгі операцияларды білу.

Қажетті құрылғы: Дербес компьютер.

Өткізу орны: Компьютерліксынып.

Уақыт: 2 сағат.

Санау жүйесі деп сандарды жазу мен атауын қабылдау жиыныайтамыз. Кез келген санау жүйесінде сандарды көрсету кейбіреуінде символдармен таңдалады, ал қалған сандарды көрсету сандарға операцияларды қолдану кезінде пайда болады.

Санау жүйесі позициялық деп аталады, егер көрсетілген әрбір сан мағынасы тізбектелген санның позициясына қатысты өзгерсе.

Санау жүйесінің позициялық негізі деп бірлік санының қандай да бір разрядын, жоғары разрядтан көп бірлікті біріктіруі аталады. Егер осындай сандардың жиыны Р - ға тең болса, онда санау жүйесі Р -лық жүйе деп аталады. Осы санау жүйесіндегі қолданылатын сандар жазбасы санау жүйесіндегі сандар жиынымен сәйкес келеді.

х еркін санының жазбасы Р-лық позициялық санау жүйесінде көпмүше түрінде неізделеді:

x = a n P n + a n -1 P n -1 + . . . + a 1 P 1 + a 0 P 0 + a -1 P -1 + . . . + a -m P -m

Кез келген санау жүйесіне арифметикалық амал қолдану ондық жүйедегі сияқты ереже бойынша орындалады. Сондықтан мәліметтерге сәйкес келетін Р - лық санау жүйесіне негізделген қосу және көбейту таблицаларын ғана қолдану керек.

Ондық санау жүйесінен P > 1 жүйесіне ауыстыру үшін келесі алгоритм қолданылады:

1) егер санның бүтін бөлігі ауыстырылса, онда ол Р- ға бөлінеді, кейін бөліндіден қалған қалдық сақталынады. Алынған бөлік тағы да Р- ға бөлнеді, қалдық сақталады. Бұл процедура 0-ге тең болғанынша жалғаса береді. Р- ға бөлгендегі алынған қалдық керісінше қатарда жазылады;

2) егер де бөлшек бөлігі ауыстырылса, онда ол Р- ға көбейтіледі, кейін бүтін бөлігі сақталады және кері қайтарылады. Жаңа алынған бөлшек бөлімі P көбейтіледі. Бөлшек бөлігі ноль болғанша процедура жүзеге аса береді.

Есептерді шығару мысалдары :

1. Берілген санды екіліктен ондық санау жүйесіне ауыстыру:
а) 464 (10) ; б) 380, 1875 (10) ; в) 115, 94 (10) (екілік түрде үтірден кейін бес мән алу) .

Шешімі.

464 0 380 0 1875 115 1 94

232 0 190 0 0375 57 1 188

116 0 95 1 075 28 0 176

58 0 47 1 15 14 0 152

а) 29 1 б) 23 1 10 в) 7 1 104

14 0 11 1 3 1 008

7 1 5 1 1 1 016

3 1 2 0

1 1 1 1

а) 464 (10) = 11101 (2) ; б) 380, 1875 (10) = 1000, 0011 (2) ; в) 115, 94 (10) ≈ 1110011, 0 (2) (осы жағдайда үтірден кейін алты мән алынды, содан кейін шешім жуықтап алынды) .

Егер екілік санау жүйесідегі санды санау жүйесіне ауыстыру керек болса, негізі екінің дәрежесі болып табылатын, онда төмендегі алгоритмді қолданып, дәреже көрсетіші қанша болса сонша екілік санының сандарын топқа біріктіру жеткілікті болады. Мысалы, егер сегіздік жүйеге ауыстыру жүзеге асса, онда топ үш саннан тұратын болады (8 = 2 3 ) . Сонымен, бүтін бөлікте оңнан солға қарай, бөлшек бөлігінде солдан оңға қарай топтастыру жүргіземіз. Соңғы топта сандар жеткіліксіз болса нолдеді жазмаз: бүтін бөлікте -сол жақтан, бөлшек бөлігінде - оң жақтан. Кейін әр бір топ жаңа жүйенің тиісті номерімен ауыстырылады. Тиісінше кетелерде көрсетілген.

P
2
00
01
10
11
4
0
1
2
3
P
2
000
001
010
011
100
101
110
111
8
0
1
2
3
4
5
6
7
P
2
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
16
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F

010101, 11 (2) екілік санау жүйесінен он алтылық санау жүйесіне ауыстырымыз.

00010101 , 1100 (2) = 3D5, C (16) .

P негізделуі бар санау жүйесіндегі садарды ондық санау жүйесіне ауыстырғанда оңнан солға қарай, ноліншіден бастап, бүтін бөліктің разрядын номерлеу керек, және бөлшек бөлігіндеүтірден кейінгі разрядтан бастапоңнан солға қарай (бастапқы номер -1) номерлеу қажет. Содан кейін разряд номеріне тең, дәрежедегі санау жүйесіне негізделе отырып разрядтардың тиісті мәндерінің туындылар қосындысын есептеңіз. Бұл берілген санның ондық санау жүйесіндегі көрінісі болып табылады.

2. Берілген санды ондық санау жүйесіне ауыстырыңыз.

а) 11 (2) .

11 (2) =1*2 6 +0*2 5 +0*2 4 +0*2 3 +0*2 2 + 0*2 1 +1*2 0 = 64+1=65 (10) .

Ескерту. Қанайда бір разрядта ноль саны түрса, онда ол қосындыны елемеуге болады.

б) 1, 0101 (2) .

1, 0101 (2) =1*2 9 + 1*2 4 + 1*2 3 + 1*2 2 + 1*2 1 + 1*2 0 + 1*2 -2 + 1*2 -4 = 512 + 16 + 8 + 4 + 2 + 1 + 0, 25 + 0, 0625 = 543, 3125 (10) .

в) 1216, 04 (8) .

1216, 04 (8) =1*8 3 +2*8 2 +1*8 1 +6*8 0 +4*8 -2 = 512+128+8+6+0, 0625 = 654, 0625 (10) .

г) 29A, 5 (16) .

29A, 5 (16) = 2*16 2 +9*16 1 +10*16 0 +5*16 -1 = 512+144+10+0, 3125 = 656, 3125 (10) .

P негізделуі бар санау жүйесінде арифметкалық операцияларды орындау үшін тиісті қосу және көбейту кестелері болу керек. P = 2, 8 және 16 үшін кестелер төменірек көрсетілген.

Р =2

:
:
:
:
:
:
+
0
1
0
0
1
1
1
10
:
:
:
:
:
:
×
0
1
0
0
0
1
0
1
+010011110:
+:
0:
+010011110:
+:
0:

Р =8

:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
+
0
1
2
3
4
5
6
7
0
0
1
2
3
4
5
6
7
1
1
2
3
4
5
6
7
10
2
2
3
4
5
6
7
10
11
3
3
4
5
6
7
10
11
12
4
4
5
6
7
10
11
12
13
5
5
6
7
10
11
12
13
14
6
6
7
10
11
12
13
14
15
7
7
10
11
12
13
14
15
16
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
×
0
1
2
3
4
5
6
7
0
0
0
0
0
0
0
0
0
1
0
1
2
3
4
5
6
7
2
0
2
4
6
10
12
14
16
3
0
3
6
11
14
17
22
25
4
0
4
10
14
20
24
30
34
5
0
5
12
17
24
31
36
43
6
0
6
14
22
30
36
44
52
7
0
7
16
25
34
43
52
61
+012345670012345671123456710223456710113345671011124456710111213556710111213146671011121314157710111213141516:
+:
0:
1:
2:
3:
4:
5:
6:
+012345670012345671123456710223456710113345671011124456710111213556710111213146671011121314157710111213141516:
+:
0:
1:
2:
3:
4:
5:
6:
+012345670012345671123456710223456710113345671011124456710111213556710111213146671011121314157710111213141516:
+:
0:
1:
2:
3:
4:
5:
6:
+012345670012345671123456710223456710113345671011124456710111213556710111213146671011121314157710111213141516:
+:
0:
1:
2:
3:
4:
5:
6:
+012345670012345671123456710223456710113345671011124456710111213556710111213146671011121314157710111213141516:
+:
0:
1:
2:
3:
4:
5:
6:
+012345670012345671123456710223456710113345671011124456710111213556710111213146671011121314157710111213141516:
+:
0:
1:
2:
3:
4:
5:
6:
+012345670012345671123456710223456710113345671011124456710111213556710111213146671011121314157710111213141516:
+:
0:
1:
2:
3:
4:
5:
6:
+012345670012345671123456710223456710113345671011124456710111213556710111213146671011121314157710111213141516:
+:
0:
1:
2:
3:
4:
5:
6:

Р =16

+
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
+: 0
0: 0
1: 1
2: 2
3: 3
4: 4
5: 5
6: 6
7: 7
8: 8
9: 9
A: A
B: B
C: C
D: D
E: E
F: F
+: 1
0: 1
1: 2
2: 3
3: 4
4: 5
5: 6
6: 7
7: 8
8: 9
9: A
A: B
B: C
C: D
D: E
E: F
F: 10
+: 2
0: 2
1: 3
2: 4
3: 5
4: 6
5: 7
6: 8
7: 9
8: A
9: B
A: C
B: D
C: E
D: F
E: 10
F: 11
+: 3
0: 3
1: 4
2: 5
3: 6
4: 7
5: 8
6: 9
7: A
8: B
9: C
A: D
B: E
C: F
D: 10
E: 11
F: 12
+: 4
0: 4
1: 5
2: 6
3: 7
4: 8
5: 9
6: A
7: B
8: C
9: D
A: E
B: F
C: 10
D: 11
E: 12
F: 13
+: 5
0: 5
1: 6
2: 7
3: 8
4: 9
5: A
6: B
7: C
8: D
9: E
A: F
B: 10
C: 11
D: 12
E: 13
F: 14
+: 6
0: 6
1: 7
2: 8
3: 9
4: A
5: B
6: C
7: D
8: E
9: F
A: 10
B: 11
C: 12
D: 13
E: 14
F: 15
+: 7
0: 7
1: 8
2: 9
3: A
4: B
5: C
6: D
7: E
8: F
9: 10
A: 11
B: 12
C: 13
D: 14
E: 15
F: 16
+: 8
0: 8
1: 9
2: A
3: B
4: C
5: D
6: E
7: F
8: 10
9: 11
A: 12
B: 13
C: 14
D: 15
E: 16
F: 17
+: 9
0: 9
1: A
2: B
3: C
4: D
5: E
6: F
7: 10
8: 11
9: 12
A: 13
B: 14
C: 15
D: 16
E: 17
F: 18
+: A
0: A
1: B
2: C
3: D
4: E
5: F
6: 10
7: 11
8: 12
9: 13
A: 14
B: 15
C: 16
D: 17
E: 18
F: 19
+: B
0: B
1: C
2: D
3: E
4: F
5: 10
6: 11
7: 12
8: 13
9: 14
A: 15
B: 16
C: 17
D: 18
E: 19
F: 1A
+: C
0: C
1: D
2: E
3: F
4: 10
5: 11
6: 12
7: 13
8: 14
9: 15
A: 16
B: 17
C: 18
D: 19
E: 1A
F: 1B
+: D
0: D
1: E
2: F
3: 10
4: 11
5: 12
6: 13
7: 14
8: 15
9: 16
A: 17
B: 18
C: 19
D: 1A
E: 1B
F: 1C
+: E
0: E
1: F
2: 10
3: 11
4: 12
5: 13
6: 14
7: 15
8: 16
9: 17
A: 18
B: 19
C: 1A
D: 1B
E: 1C
F: 1D
+: F
0: F
1: 10
2: 11
3: 12
4: 13
5: 14
6: 15
7: 16
8: 17
9: 18
A: 19
B: 1A
C: 1B
D: 1C
E: 1D
F: 1E
×€
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
×€: 0
0: 0
1: 0
2: 0
3: 0
4: 0
5: 0
6: 0
7: 0
8: 0
9: 0
A: 0
B: 0
C: 0
D: 0
E: 0
F: 0
×€: 1
0: 0
1: 1
2: 2
3: 3
4: 4
5: 5
6: 6
7: 7
8: 8
9: 9
A: A
B: B
C: C
D: D
E: E
F: F
×€: 2
0: 0
1: 2
2: 4
3: 6
4: 8
5: A
6: C
7: E
8: 10
9: 12
A: 14
B: 16
C: 18
D: 1A
E: 1C
F: 1E
×€: 3
0: 0
1: 3
2: 6
3: 9
4: C
5: F
6: 12
7: 15
8: 18
9: 1B
A: 1E
B: 21
C: 24
D: 27
E: 2A
F: 2D
×€: 4
0: 0
1: 4
2: 8
3: C
4: 10
5: 14
6: 18
7: 1C
8: 20
9: 24
A: 28
B: 2C
C: 30
D: 34
E: 38
F: 3C
×€: 5
0: 0
1: 5
2: A
3: F
4: 14
5: 19
6: 1E
7: 23
8: 28
9: 2D
A: 32
B: 37
C: 3C
D: 41
E: 46
F: 4B
×€: 6
0: 0
1: 6
2: C
3: 12
4: 18
5: 1E
6: 24
7: 2A
8: 30
9: 36
A: 3C
B: 42
C: 48
D: 4E
E: 54
F: 5A
×€: 7
0: 0
1: 7
2: E
3: 15
4: 1C
5: 23
6: 2A
7: 31
8: 38
9: 3F
A: 46
B: 4D
C: 54
D: 5B
E: 62
F: 69
×€: 8
0: 0
1: 8
2: 10
3: 18
4: 20
5: 28
6: 30
7: 38
8: 40
9: 48
A: 50
B: 58
C: 60
D: 68
E: 70
F: 78
×€: 9
0: 0
1: 9
2: 12
3: 1B
4: 24
5: 2D
6: 36
7: 3F
8: 48
9: 51
A: 5A
B: 63
C: 6C
D: 75
E: 7E
F: 87
×€: A
0: 0
1: A
2: 14
3: 1E
4: 28
5: 32
6: 3C
7: 46
8: 50
9: 5A
A: 64
B: 6E
C: 78
D: 82
E: 8C
F: 96
×€: B
0: 0
1: B
2: 16
3: 21
4: 2C
5: 37
6: 42
7: 4D
8: 58
9: 63
A: 6E
B: 79
C: 84
D: 8F
E: 9A
F: A5
×€: C
0: 0
1: C
2: 18
3: 24
4: 30
5: 3C
6: 48
7: 54
8: 60
9: 6C
A: 78
B: 84
C: 90
D: 9C
E: A8
F: B4
×€: D
0: 0
1: D
2: 1A
3: 27
4: 34
5: 41
6: 4E
7: 5B
8: 68
9: 75
A: 82
B: 8F
C: 9C
D: A9
E: B6
F: C3
×€: E
0: 0
1: E
2: 1C
3: 2A
4: 38
5: 46
6: 54
7: 62
8: 70
9: 7E
A: 8C
B: 9A
C: A8
D: B6
E: C4
F: D2
×€: F
0: 0
1: F
2: 1E
3: 2D
4: 3C
5: 4B
6: 5A
7: 69
8: 78
9: 87
A: 96
B: A5
C: B4
D: C3
E: D2
F: E1

3. Қосуды орындаңыз:

а) 1100 (2) + 11110 (2) = 10111000110 (2) .
б) 223, 2 (8) + 427, 54 (8) = 652, 74 (8) .
в) 3B3, 6 (16) + 38B, 4 (16) = 73E, A (16) .

1100 223, 2 3B3, 6

+ 11110 + 427, 54 +38B, 4

10111000110 652, 74 73E, A

4. Азайтуды орындаңыз:

а) 1111, 011 (2) - 101010111, 1 (2) = 110101011, 111 (2) .
б) 1510, 2 (8) - 1230, 54 (8) = 257, 44 (8) .
в) 27D, D8 (16) - 191, 2 (16) = EC, B8 (16) .

1111, 011 1510, 2 27D, D8

- 101010111, 1 -1230, 54 -191, 2

110101011, 111 257, 44 EC, B8

5. Көбейтуді орындаңыз:

а) 100111 (2) * 1000111 (2) = 101011010001 (2) .
б) 1170, 64 (8) * 46, 3 (8) = 57334, 134 (8) .
в) 61, A (16) * 40, D (16) = 18B7, 52 (16) .

100111 1170, 64 61, A

*1000111 * 46, 3 *40, D

100111 355 234 4F 52

+ 100111 + 7324 70 + 1868

100111 47432 0

100111 18B7, 52

57334, 134

101011010001

Тапсырмалар:

  1. Сандарды ондық санау жүйесіне ауыстырып, қайта ауыстыру арқылы шыққан мәнді тексеріңіз:
110100, 11 2 ;
123, 41 8 ;
1DE, C8 16 .
  1. Екілік санау жүйесіндегі сандарды сегіздік және он алтылық санау жүйесіне ауыстырып, қайта ауыстыру арқылы шыққан мәнді тексеріңіз:
1000111, 0111 2 ;
100011100, 11 2 ;
1000111, 01112;:
100011100, 112;:
  1. Сандарды қосып, тиісті ондық қосуды орындап шыққан мәнді тексеріңіз:
1011 2 , 11 2 и 111, 1 2 ;
7, 5 8 и 14, 6 8 ;
A, B 16 и E, F 16 ;
  1. Сандарды көбейтіп, тиісті ондық көбейтуді орындап шыққан мәнді тексеріңіз:
101 2 и , 001 2 ;
6, 25 8 и 7, 12 8 .
  1. Мәнін табыңыз:

1010 10 + (106 16 - 11011101 2 ) - 12 8 ;

Ондық санау жүйесіндегі 59 саны басқа санау жүйесіндегі 214 санына тең. Осы санның негіздлуін табыңыз.


Практикалық жұмыс №2. Логикалық жүйелер.

Мақстаты : логикалық функцияларды жүйелер түріне келтірудің әдістерін білу, олардың өзгертілуі және логикалық операциялар.

Жұмыс мақсаты:

- логикалық элементтердің алгебра логикасы функциясының (АЛФ) элементтеріне ауысуын теориялық жағынан тану;

- К155 отандық микросхема сериясында логикалық элементтерін эксперименталды зерттеу.

2. Негізгі теориялық мағлұматтар.

2. 1. Цифрлық элекрониканың және еспетеу техникасының математикалық негізі логика алгебрасы және алгебра булевасы (Джон Буль американдық математик құрметіне) .

Булевалық алгебрада тәуелсіз айнымалылардың немесе (Х) аргументінің екі мәні бар: 0 немесе 1. Тәуелді айнымалылар немесе (У) функциялары екі мәннен текбіреуін қабылдай алады: 0 немесе 1. Алгебра логикасының функциясы (АЛФ) келесі түрде көрсетіледі:

Y = F (X1; X2; X3 . . . XN ) .

Берілген АЛФ формасы алгебралық деп аталады.

2. 2. Негізгі логикалық функциялар:

- Логикалық терістеу (инверсия)

Y = ;

- логикалық қосу (дизьюнкция)

Y = X1 + X2 или Y = X1 V X2 ;

  • Логикалық көбейту (коньюнкция)

Y = X1 · X2 или Y = X1 L X2 .

Қиын алгебра логикасының функцияларына келесілер жатады:

  • Теңмәнді функция (эквивалентті)

Y = X1 · X2 + или Y = X1 ~ X2 ;

- теңмәнді емес функция (модуль арқылы қосу)

Y = X1 · 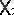+ · X2 или Y = X1 X2 ;

- Пирс функциясы (терістеу арқылы логикалық қосу)

Y = ;

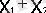- Шеффер функциясы (терістеу арқылы логикалық көбейту)

Y = ;

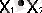2. 3. Булевалық алгебра үшін келесі заңдар мен ережелер тәуелді:

- бөлу заңы

X1 (X2 + X3) = X1 · X2 + X1 · X3,

X1 + X2 · X3 = (X1 + X2) (X1 + X3) ;

- қайталану ережесі

X · X = X, X + X = X ;

- терістеу ережесі

X · = 0, X + = 1 ;

- де Морган теоремасы

= , = ;

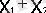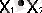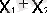- тождества

X · 1 = X, X + 0 = X, X · 0 = 0, X + 1 = 1.

2. 4. Логикалық функцияларды құрастыратын жүйелерді логикалық элементтер деп атайды. Негізгі логикалық элементтердің бір шығысы (Y) және (X1; X2; X3 . . . XN ) аргуметтер санына тең бірнеше кірісі болады. Электрлы сызбаларда логикалық элементтер тікбұрыш түрінде беріледі, кірістік (сол) және шығыстық (оң) ауыспалы болады. Тікбұрыштың ішінде символдар көрсетіледі, элементтің функционалды мағынасын білдіреді.

1 суретте, 10 элементтер көрсетілген, п. 2. 2 функциялардың орындалуы берілген. Соның ішінде кестенің күйі немесе ақиқаттық кестесі, екілік кодтағы логикалық функцияның кірістік және шығыстық өзгерістерін бейнелейді. Ақиқат кестесі ФАЛ тапсырмасының кестелік түрі болып табылады.

1 суретте “НЕ” эементті көрсетілген, логикалық терістеу Y = .

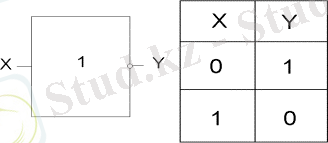
1 сурет

Элемент “НЕМЕСЕ” (2 сурет) немесе элемент “ЖӘНЕ” (3 сурет), функцияның логикалық бөлуін және логикалық көбейтуін орындайды.

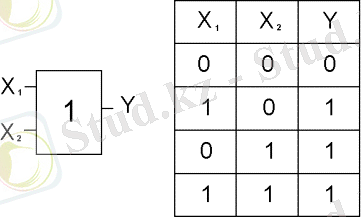
2 сурет

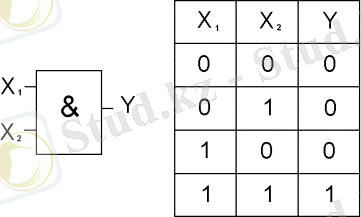
3 сурет

Пирс және Шеффер функциясы “НЕМЕСЕ-НЕ” и “ЖӘНЕ-НЕ” элементтерімен орындалады, 4 және 5 суретте көрсетілген

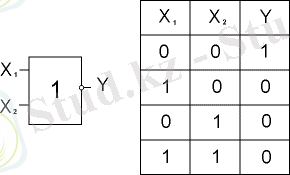
4 сурет

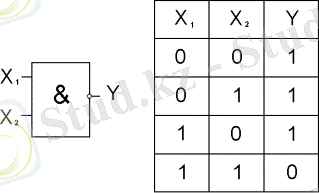
5 сурет

Пирс элементін “НЕМЕСЕ” және “НЕ” (6 сурет) элемент түрінде көрсетуге болады, ал Шеффер элементі кезекті қосылғыш элемент “ЖӘНЕ” және “НЕ” элемент түрінде болады (7 сурет) .

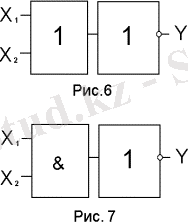
8 және 9 суретте “Ерекшелеу НЕМЕСЕ” және “Ерекшелеу НЕМЕСЕ - НЕ” элементтері көрсетілген, мұнда функцияның теңсіздік функциясы және терістеу тенсіздігі орындалады.

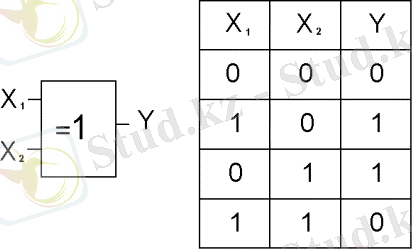
8 сурет

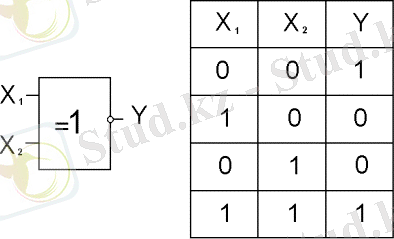
9 сурет

2. 5. Логикалық элементтер, коньюкция, дизьюнкция, Пирс және Шеффер функциялардың орындау операциясы, ортақ жағдайда болуы мүмкін, n - кірісі. Мысалға, үш кірісті логикалық элементтер, Пирс функциясын орындайды, 10 суретте көрсетілген.

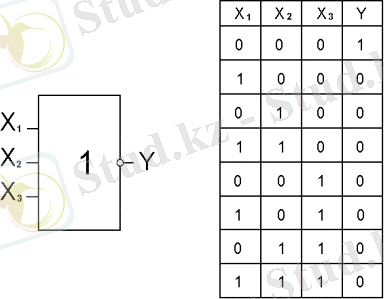
10 сурет

Ақиқат кестесінде (10 сурет) п. 2. 4 кестесінен қарағанда Y айнымалының сегіз шығысық мағынасы бар. Бұл комбинация N айнымалылардың кірістік комбинациялары арқыла анықталады, ортақ мағынада, тең: N = 2 n, онда n - айнымалылардың кіріс саны.

2. 6. Логикалық элементтер интегралды микросызбаларды құруға қолданылады, әр түрлі логикалық және арифметикалық операцияларда және де фукнцияналды бағыттарда орындалады. Микросызба К155ЛН1 типті және К155ЛА3, мысалы, өзінің құрамында алты инвертор және төрт Шеффер элементі бар (11 сурет), ал микросызба К155ЛР1 әр түрлі элеметтерден тұрады (12 сурет) .

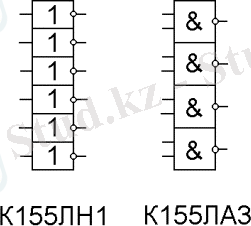
11 сурет

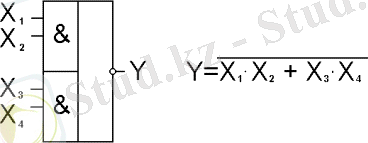
12 сурет

2. 7. ФАЛ арқылы кез келген логикалық қиын элементтерді орындауға болады. Мысал ретінде ФАЛ, алгебралық түрде берілген формуланы қарастырамыз:

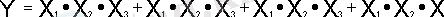. (1)

ФАЛ арқылы жеңілдетеміз, үстіде көрсетілеген ережемен шешімді аламыз:

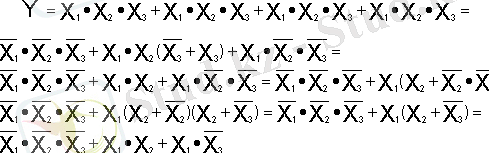(2)

Жүргізілген операция ФАЛ минималдау атына ие және функцияналды сызбаның орындау процедурасын жеңілдетуге арналған цифрлы құрылғы.

Функционалды сызба құрылымы, көрсетіген ФАЛ қарастырылады 13 суретте берілген.

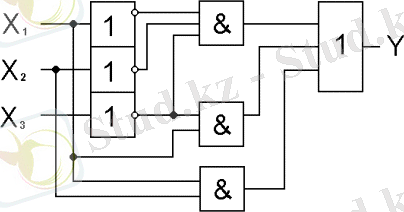
13 сурет

Айта келе, мұндағы алынған (2) функцияның құрылуы толыққанды мималданған болып саналмайды. Толық минималды функция тек лабораториялық жұмыс кезінде орындалады.

Есеп берудің мазмұны

1. Аты және жұмыс мақсаты

2. Логикалық есептердің зерттеу сызбасы

3. Логикалық формулалар және оларды минималдау

Бақылау сұрақтары

1. Алгебра логикасы қандай айнымалылармен жұмыс істейді?

2. ФАЛ-дың негізгі тапсырмалары

3. Негізгі логикалық функцияның алгебралық түрі

4. “логикалық элемент” дегеніміз не?

5. Пирс және Шеффер элементтерін орындауға қандай логикалық функциялар керек?

6. Логикалық элемент үшін кірістік айнымалы комбинацияның саны қалай анықталады?

Қолданылған әдебиеттер

Электротехника и основы электроники. О. А. Антонова, О. П. Глудкин и др., Под ред. проф. О. П. Глудкина. -М. :Высшая школа, 1993.

Практикалық жұмыс №3: Жүйелік блогқа құрылғының қосылуы және жүйелік блог компонеттерін меңгеру.

Мақсаты: негізгі блоктарды білу және персоналды компьютердің перефериялық құрылғысы, оларды қосу әдістері, конструкторлары, негізгі сипаттамасы (аты, разъем типі, контактылар саны, жіберілу мәліметтерінің жылдамдығы, қосымша қасиет) ; разъемдардың сыртқы түрлерінің тпитерін анықтауға үйрену, оларға қосылған құралдар, персоналды компьютердің негізгі құрылғыларын білу, олардың орналасуы және негізгі сипаттамасы, жүйелік блоктың сыртқы түрінің компоненттерін, тәртібін анықтау және оларды қосу тәсілдері.

Құрылғылар: жүйелік блок, кабельдар жиыны, монитор, пернетақта, перифериндік құрылғы әртүлі разъемдарға арналған (тышқан, принтер, модем және т. б. ) . жүйелік блок құрамы, видеоадаптер макеті, аналық плата, корпустар, қатқыл диск, накопителя на флоппи-дисках, интерфейстіккабелдер.

Өткізу орны:

Уақыты: 2 сағат.

Орындаутәртібі:

  1. Компьютерлік жүйе желіден ажыратылғанына көз жеткізу (қажет болған жағдайда жүйені желіден өшіріңіз) .
  2. Жүйелік болктың артқы жағын өзіңізге бұрыңыз.
  3. USB разъемінің бар жоғының аналық платасының форм-факторын анықтау.
  4. Орнын анықтап және сипаттамасын келесі разъемдарда көрсетілуі:
  • Жүйелік блоктың желіге қосылуы;
  • Монитордың желіге қосылуы;
  • Монитордың дыбыс желісі;
  • пернетақта;
  • порт кезектері (екі разъем) ;
  • параллель порт;
  • басқа да разъемдар.
  1. Барлық разъемдар жүйелік блоктың артына ауыстырылғанына көз жеткізіңіз, әр базалық құрылғылар бір жалғыз әдіспен қосылады.
  2. Тышқанның қосылу әдісін зерттеңіз.

Тышқан разъемға порт тәтібімен қосылады әлде арнайы портқа PS/2 домалақ формасы бар разъем. Соңғы әдісі жаңаланған және ыңғайлы болып келеді. Бұл жағдайда тышқан өзіндік белгілеу порты орын алады. Ақырғы модельдер клавиатураға USBинтерфейсі разъемыарқылы қосыла алады.

  1. Кестені толтырыңыз:
Разъем
Разъем типі
Контакт көлемі
Ескертулер
Разъем:
Разъем типі:
Контакт көлемі:
Ескертулер:
Разъем:
Разъем типі:
Контакт көлемі:
Ескертулер:
  1. Дербес компьютердің негізгі құрылғыларын анықтаңыз.
  2. Қоректендіру блогының орнын орнатып, қоректендіру блогының қуатын тексеріңіз (сілтемеде көрсетілген) .
  3. Аналық платаның орнын орнатыңыз.
  4. Аналық платаның жүйелік блогқа қосылуының сипаттамасын орнатыңыз Аналық платаға АТ форм-факторында қоректендірудің қосылуы екі разъеммен орындалады. Қара түсті өткізгіштің орналасуына көңіл аударыңыз - ол разъемдардың дұрыс бірігуіне маңызды.
  5. Қатқыл дисктің орнын орнатыңыз.

Оның қоректендіру разъемының орнын орнатыңыз. Қатқыл дисктің аналық платамен байланысатын өткізгіштің шлейф бағытын бақылаңыз. Қызыл бояуға боялған өткізгіштің орналасуына көңіл аударыңыз (ол қатқыл дискта қорек разъемының жанында орналасу керек.

  1. CD-ROM дисководы мен иілгіш дисктардың дисководының орнын орнатыңыз. Олардың өткізгіш шлейфтерінің бағытын бақылыңыз және қызыл түске боялған өткізгіштің жағдайларына көңіл аударыңыз.
  2. Бейнеадаптер платасының орнын орнатыңыз. Бейнеадаптер платасының интерфейс типін анықтаңыз.
  3. Егер қосымша құрылғылар болса, олардың тағайындалуын анықтап, берілген құрылғылардың сипаттамалық ерекшеліктерін жазыңыз(разъем типі, интерфейс типі және т. б) .
  4. Кестені толтырыңыз:
Құрылғы
Сипаттамалық ерекшеліктер
Ненің көмегімен және қайда қосылады
Құрылғы:
Сипаттамалық ерекшеліктер:
Ненің көмегімен және қайда қосылады:

Қорғау сұрақтары:

  1. Есептеу жүйесінің архитектурасы.
  2. Жүйелік блогтың құрамы.
  3. Тағайындалу, негізгі сипаттамалары, дербес компьютердің құрылғы интерфейсі ( әр құрылғы бойынша) .
  4. Қатқыл дисктің құрылғысы.
  1. Базалық аппараттық конфигурация;
  2. Монитордың негізгі сипаттамалары;
  3. Разъемдардың сипаттамалары ( разъем типі, контакт көлемі, мәліметтерді жіберу жылдамдығы: бейнеадаптерлердің; кезекті порттардың; параллельді потрттардың; USB шиналары; желілік карталары; жүйелік блогтың қорегі; монитор қорегі.

Қосалқы құрылғылардың типі.

Практикалық жұмыс№4: Аналық платаның компонеттерін меңгеру.

Мақсаты: Дербес компьютердің аналық платасында орналасқан құрылғыны білу.

Құрал - жабдықтар: аналық платаның макеті, процессорлар, оперативтіжадының модулдері.

Өту орны:

Уақыты: 2 сағат.

Орындалу реті:

  1. Компьютерлік жүйе токтан ажыратылғанына көз жеткізіңіз (қажетінше жүйені желіден ажыратыңыз) .
  2. Процессордың орнын орнатыңыз және оның ұйымдастыру жүйесінің салқындауын меңгеріңіз. Маркерлеу бойынша процессор типін және өндіру фирмасын анықтаңыз.
  3. Оперативті жадының модулдерін орнату үшін разъемның орнын орнатыңыз. Олардың көлемін және қолданылып отырған модулдер типін (DIMM немесе SIMM) анықтап, контакт көлемін орнатыңыз.
  4. Кеңейтілу платасын орнату үшін слоттардың орнын орнатыңыз. Олардың көлемін жәнетиптерін(ISA, VLB, PCI, AGP) анықтап, контакт көлемін орнатыңыз. Олардың түсі мен форма бойынша айырмашылығын тіркеңіз:
Шина разъемы
Түсі
Өлшемі
Шина разъемы: ISA
Түсі: қара
Өлшемі: ұзын
Шина разъемы: PCI
Түсі: ақ
Өлшемі: орташа
Шина разъемы: AGP
Түсі: қоңыр
Өлшемі: қысқа
  1. Тұрақты есте сақтау құрылғысының микросхемасының орнын орнатыңыз Установите местоположение микросхемы ПЗУ. Ондағы жабыстырмасы бойынша берілген компьютердің BIOS жүйесінің өндірушісін анықтаңыз.
  2. Жүйелік комплектың (чипсеттің) микросхемасының орнын орнатыңыз. Белгіленуі бойынша комплектің типін және шығарушының фирмасын анықтаңыз.
  3. Қорытынды кестені толтырыңыз:
Өңдіруші
Моделі
: Процессор
Өңдіруші:
Моделі:
: Чипсет
Өңдіруші:
Моделі:
: BIOS жүйесі
Өңдіруші:
Моделі:
Жедел жады модульінің өлшем саны
Кеңейтілу платасын орнату үшін слоттар саны
Жедел жады модульінің өлшем саны: SIMM
Кеңейтілу платасын орнату үшін слоттар саны: DIMM
ISA
PCI
AGP

Қорғау сұрақтары:

  1. Қомпьютермен жұмысты басқаратын электронды платаның типтері;
  2. Аналық платаның негізгі сипаттамасы;
  3. Аналық платада орналасқан қондырғылар және олардың сипаттамалары;
  4. Шин сипаттамасы - қосылған қондырғының типі, мәліметтер берудің жылдамдығы.
  5. Контроллер және адаптер, оларды белгілеу және негізгі сипаттамалары;

Практикалық жұмыс№5: Компьютерді іске қосу тәртібін зерттеу.

Мақсаты: компьютердің бастапқы жүктеу тәртібін анықтау, оның этаптарын білу, орындалмаудың болуы және олардың диагностикалық методы.

Құрылғылар: компьютер жиынтығы, немесе сынама тақша.

Өту орны:

Уақыты: 2 сағат.

Базалық мәліметтер:

... жалғасы
Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.
Ұқсас жұмыстар
Информатикадан сыныптан тыс жұмыстың ерекшеліктері
ИФОРМАТИКА САБАҒЫН ОҚУШЫЛАРҒА ҚОСЫМША ОҚЫТУ
Информатикадан сыныптан тыс жұмыстардың түрлері
Сыныптан тыс жұмысты ұйымдастыру түрлері
Мектеп информатика курсы бойынша өткізілетін дәстүрден тыс сабақтың мақсаты
Информатикадан сыныптан тыс жұмыстарды ұйымдастыру
Информатикадан зертханалық және практикалық жұмыстарды өткізу әдістемесі
Операциялық жүйені оқыту әдістемесі
Информатиканы продуктивті оқыту әдістері
Информатикадан сыныптан тыс жұмыстардың әдістемесі
Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

google play appstore

instagram tiktok

Ақпарат

Қосымша


Email: info@stud.kz



Реферат Курстық жұмыс Диплом Материал Диссертация Практика Презентация Сабақ жоспары Мақал-мәтелдер 1‑10 бет 11‑20 бет 21‑30 бет 31‑60 бет 61+ бет Негізгі Бет саны Қосымша Іздеу Ештеңе табылмады :( Соңғы қаралған жұмыстар Қаралған жұмыстар табылмады Тапсырыс Антиплагиат Қаралған жұмыстар kz