Екі еркіндік дәрежесі бар механикалық жүйенің еркін тербелістерін зерттеу

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 9 бет
Таңдаулыға:

Мазмұны

I. Кіріспе

1. 1. Динамикалық жүйелер

1. 2. Еркін тербелістер

1. 3. Екі еркіндік дәрежесі бар механикалық жүйенің еркін тербелістерін зерттеу. .

II. Қорытынды

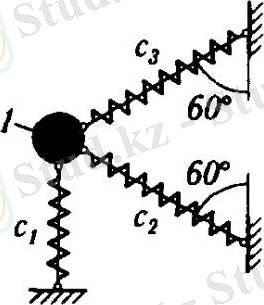
Екі еркіндік дәрежесі бар механикалық жүйенің еркін тербелістерін зерттеу

Д-4 вариант 3

Берілгені:

m₁=4 кг, с₁=30 Н/см, с₂=20 Н/см, с₃= 10 Н/см

Табу керек: к₁, к₂- нің тербеліс формасын-?

$Шешу\ \ жолы:\ \ \$

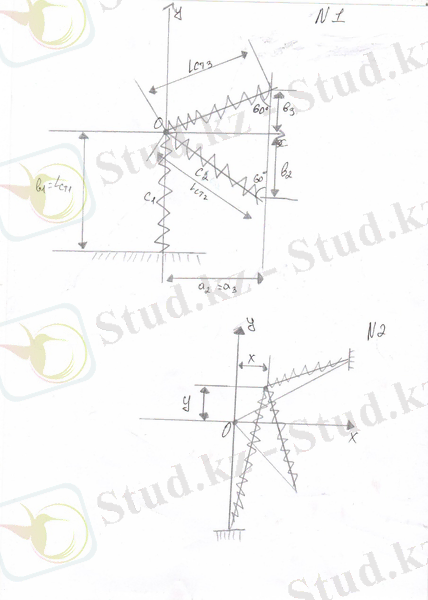
Жүйенің екі еркіндік дәрежесі бар, координаталарды жалпылау ретінде мен мынаны қабылдаймын: х-ті қайтадан Х осьіне ауыстырамын, у-ті қайтадан У осьіне ауыстырамын.

Енді кинетикалық және потенциалдық энергия жүйесін табамын.

КИНЕТИКАЛЫҚ энергия :

Жүйенің потенциалдық энергиясы потенциалдық энергия деформациясын қолдану арқылы анықталады. Ауырлық күші әсер етпейді, өйткені қозғалыс көлденең жазықтықта жүреді.

Π=Π₁+Π₂+Π₃

Серіппелі деформация: $\lambda_{і =}l_{і -}l_{сті}$

$l_{і}$ - серіппе ұзындығының деформациясы, $l_{сті}$ - статикалық тепе-теңдіктегі деформацияланбаған серіппенің ұзындығы

Серіппенің шартты-статикалық деформациясы бойынша=0

Нүктелік координатты белгілейік:

$а_{і}, b_{і}; \ \ \ \ х, у - m\$ н үктесінің координатасы.

Енді 2 сурет арқылы серіппенің ұзындығын табамыз?

$l_{і} = \sqrt{{(х - а_{і}) }^{2} + {(у - b_{і}) }^{2}} = \sqrt{х^{2} + у^{2} - 2\left( ха_{і} + {уb}_{і} \right) + а_{і}^{2} + b_{і}^{2}} = l_{cті}\sqrt{1 - \frac{2\left( ха_{і} + уb_{b} \right) }{l_{сті}^{2}} + \frac{х^{2} + у^{2}}{l_{сті}^{2}}}$

Қатардағы түбірді бөліп жазамыз:

${(1 + z) }^{\frac{1}{2}} = 1 + \frac{1}{2}z - \frac{1}{2*4}z^{2} + \ldots$

$z = \frac{x^{2} + y^{2} - 2({ха}_{і} + {уb}_{і}) }{l_{сті}^{2}}$

Екінші дәрежеден жоғары мәндерді ескермеу, тепе-теңдік күйінен салыстырмалы түрде аз ауытқулар х, у.

$l_{і} = l_{сті}\left\lbrack 1 + \frac{1}{2}*\frac{х^{2} + у^{2} - 2\left( {ха}_{і} + {уb}_{і} \right) }{l_{сті}^{2}} \right\rbrack$ = $l_{сті} + \frac{1}{2l_{сті}}\left\lbrack х^{2} + у^{2} - 2\left( {ха}_{і} + {уb}_{і} \right) \right\rbrack$

Серіппелі деформация:

$\lambda_{і} = l_{і} - l_{сті} = \frac{1}{2l_{сті}}\left\lbrack х^{2} + у^{2} - 2\left( {ха}_{і} + {уb}_{і} \right) \right\rbrack$

Потенциалды энергия:

$\Pi_{і} = \frac{с_{і}}{2}*\lambda_{і}^{2}$

x, y-ге қатысты екінші дәрежеден жоғары болатын шамалар, одан аламыз:

$\Pi_{і} = \frac{с_{і}}{2}*\frac{1}{4l_{сті}^{2}}4\left( {ха}_{і} + {уb}_{і} \right) ^{2}$

$П = \sum_{}^{}П_{і} = \frac{1}{2}\sum_{}^{}\frac{с_{і}}{l_{сті}^{2}}\left( {ха}_{і} + {уb}_{і} \right)$

Берілген схема арқылы мынаны аламын:

а₁=0; а₂= $l_{cт2}\sin 60^{{^\circ}}$ ; а₃= $l_{ст2}\sin 60^{{^\circ}}$

b₁= $- l_{ст1}$ ; b₂= $- l_{ст2}\cos 60^{{^\circ}}$ ; b₃= $l_{ст3}\cos 60^{{^\circ}}$

Осы арқылы мен мынаны аламын:

${1) П}_{1} = \frac{1}{2}\frac{с_{1}}{l_{ст1}^{2}}*\left\lbrack х*0 + у*\left( - l_{ст1} \right) \right\rbrack^{2} = \frac{1}{2}с_{1}у^{2}$

${2) П}_{2} = \frac{1}{2}\frac{с_{2}}{l_{cт2}^{2}}\left\lbrack х*l_{cт2}*\frac{\sqrt{3}}{2} + у*\left( - l_{ст2}\frac{1}{2} \right) \right\rbrack^{2}$ = $\frac{1}{2}с_{2}\left( х^{2}\frac{3}{4} - 2ху\frac{\sqrt{3}}{2}\frac{1}{2} + у^{2}\frac{1}{4} \right)$ = $\frac{1}{2}с_{2}\left( \frac{\sqrt{3}}{2}х - \frac{1}{2}у \right) ^{2}$

3) $П_{3} = \frac{1}{2}\frac{с_{3}}{l_{ст3}}\left\lbrack хl_{ст3}\frac{\sqrt{3}}{2} + уl_{ст3}\frac{1}{2} \right\rbrack^{2} = \frac{1}{2}с_{2}\left( \frac{\sqrt{3}}{2}х + \frac{1}{2}у \right) ^{2}\$

$П = \frac{1}{2}\left\lbrack с_{1}у^{2} + \left( \frac{\sqrt{3}}{2}х - \frac{1}{2}у \right) ^{2}с_{2} + \left( \frac{\sqrt{3}}{2}х + \frac{1}{4}у \right) с_{3} \right\rbrack$

Осылайша: $Т = \frac{1}{2}\left( m_{1}ẋ^{2} + m_{1}ẏ^{2} \right)$

$П = \frac{1}{2}\left\lbrack с_{1}у^{2} + \left( \frac{3}{4}х^{2} - 2\frac{\sqrt{3}}{2}х\frac{1}{2}у + \frac{1}{4}у^{2} \right) с_{2} + \left( \frac{3}{4}х^{2} + 2\frac{\sqrt{3}}{2}х\frac{1}{2}у + \frac{1}{4}у^{2} \right) с_{3} \right\rbrack$ = $\frac{1}{2}\left\lbrack \frac{3}{4}\left( с_{2} + с_{3} \right) х^{2} + \frac{\sqrt{3}}{2}\left( с_{3} - с_{2} \right) ху + \frac{1}{4}\left( {4с}_{1} + с_{2} + с_{3} \right) у^{2} \right\rbrack$

Немесе

$Т = \frac{1}{2}\left( а_{11}ẋ^{2} + 2а_{12}ẋẏ + а_{22}ẏ^{2} \right)$

$П = \frac{1}{2}\left( с_{11}х^{2} + 2с_{22}у^{2} \right)$

Бұл жердегі $а_{11}$ - энергияның коэффициенті:

$а_{11} = М_{11}$ $а_{12} = 0\ \ \ \ \ \ \$ $а_{12} = М_{1}$

с₁- қатаңдық коэффициенті

с₁₁= $\frac{3}{4}\left( с_{2} + c_{3} \right)$ $c_{12} = \frac{\sqrt{3}}{2}\left( c_{3} - c_{2} \right) /2$ $c_{22} = \frac{1}{4}\left( 4c_{1} + c_{2} + c_{3} \right)$

Мен қарастырып отырған жүйе үшін II түрдегі Лагранж теңдеуі мына түрге ие.

$\frac{d}{dt}\left( \frac{\partial T}{\partial\dot{x}} \right) - \frac{\partial T}{\partial\dot{x}} = - \frac{\partial П}{\partial x};$ $\frac{d}{dt}\left( \frac{\partial T}{\partial\dot{y}} \right) - \frac{\partial Т}{\partial у} = - \frac{\partial П}{\partial у}$

Енді осы теңдеудегі туындыларды есептеймін:

$\frac{\partial Т}{\partial x} = 0$ $\frac{\partial Т}{\partial у} = 0$

$\frac{\partial Т}{\partial\dot{х}} = а_{11}\dot{х}$ $\frac{d}{dt}\left( \frac{\partial T}{\partial\dot{x}} \right) = а_{11}\ddot{x, \ \ }\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\partial П}{\partial x} = с_{11}х + с_{12}у$

$\frac{\partial Т}{\partial\dot{у}} = а_{22}\dot{у}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{d}{dt}\left( \frac{\partial T}{\partial\dot{y}} \right) = a_{22}\ddot{y}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\partial П}{\partial у} = с_{22}у + с_{12}х$

Шыққан туындыны Лагранждың теңдеуіне қоямыз:

$а_{11}\ddot{х} = - с_{11}х - с_{12}у$

$а_{22}\ddot{у} = - с_{22}у - с_{22}х$

Осылайша еркін тербелістердің дифференциалдық теңдеулерінің формасы мына түрде болады:

$а_{11}\ddot{х} + с_{11}х + с_{12}у = 0$

$а_{22}\ddot{у} + с_{22}у + с_{21}х = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ с_{12} = с_{21}$

Осы түрде көрсетілген теңдеулердің нақты шешімі мына түрде болады:

$x = А_{х}\sin(kt + \beta) ; \ \ \ \ \ \ \ \ \ \ \ \ \ y = A_{y}\sin(kt + \beta) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$

$А_{х}, \ А_{у} - негізгі\ тербеліс\ амплитудасы, \ \ k - жиіліксіз\ тербеліс$

β-тесбелістің бастапқы фазасы

Осы дифференциалдық теңдеулер жүйесінен шығатын жиіліктік теңдеу формасы бар:

$а_{11}а_{22}к^{4} - \left( а_{11}с_{22} + а_{22}с_{11} \right) к^{2} + \left( с_{11}с_{22} - с_{12}^{2} \right) = 0$

Осы арқылы мынаны аламын:

$с_{11} = \frac{3}{4}(2000 + 100) = 2250; \ \ \ \ \ \ \ \ с_{12} = \frac{\sqrt{3}}{4}(1000 - 2000) = - 433$

$с_{22} = \frac{1}{4}(4*3000 + 2000 + 1000) = 3750$

Жиіліктердің квадраттарына сәйкес келетін осы биквадрат теңдеудің түбірлері формулалармен анықталады:

$к_{12}^{2} = \frac{а_{11}с_{22} + а_{22}с_{11} \mp \sqrt{\left( а_{11}с_{22} + а_{22}с_{11} \right) ^{2} - 4а_{11}а_{22}\left( с_{11}с_{22} - с_{12}^{2} \right) }}{2а_{11}а_{22}} =$

$= \frac{4*3750 + 4*2250 \mp \sqrt{(4*3750 + 4*2250) ^{2} - 4*4*4(2250*3750 - 433) ^{2}}}{2*4*4}$

$к_{1}^{2} = 533, 5с^{- 2}, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ к_{2}^{2} = 966, 5с^{- 2}$

Енді теңдеудің квадратынан айырыламын, сол кезде к- мынаған тең болады:

$к_{1} = 23с^{- 1}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ к_{2} = 31с^{- 1}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$

$к_{1}$ және $к_{2}$ жиіліктеріне сәйкес келетін таралу коэффициенттерінің формасы болады.

$\mu = \frac{А_{у_{1}}}{А_{х_{1}}} = \frac{с_{11} - а_{11}к_{1}^{2}}{с_{12}} = - \frac{2250 - 4*533, 5}{- 433} = 0, 27$

$\mu = \frac{А_{у_{2}}}{А_{х_{2}}} = \frac{с_{11} - а_{11}к_{2}^{2}}{с_{12}} = - \frac{2250 - 4*966, 5}{- 433} = - 3, 7$

Бірінші негізгі тербелісті анықтайтын теңдеу мына түрде:

$х_{1} = А_{х_{1}}\sin\left( 23t + \beta_{1} \right) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ у_{1} = 0, 27A_{х_{1}}\sin\left( 23t + \beta_{1} \right)$

Екінші негізгі тербелісті анықтайтын теңдеу:

$х_{2} = А_{х_{2}}\sin\left( 31t + \beta_{2} \right) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ у_{2} = - 3, 7A_{х_{2}}\sin\left( 31t + \beta_{2} \right)$

Дифференциалдық теңдеулердің жалпы шешімі- бұл нақты шешімдердің қосындысы:

$х = х_{1} + х_{2} = А_{х_{1}}\sin\left( 23t + \beta_{1} \right) + А_{х_{2}}\sin\left( 31t + \beta_{2} \right)$

$у = у_{1} + у_{2} = 0, 27А_{х_{1}}\sin{\left( 23t + \beta_{1} \right) - 3, 7А_{х_{2}}\sin\left( 31t + \beta_{2} \right) }$

Қарастырып жатқан жүйенің 2 ретті Лагранж теңдеуін құрамыз

$\frac{d}{dt}\left( \frac{\partial T}{\partial\varphi} \right) - \frac{\partial T}{\partial\varphi_{i}} = - \frac{\partial П}{\partial\varphi_{і}}$ + $Q_{1}$ $\frac{d}{dt}\left( \frac{\partial T}{\partial\varphi_{2}} \right) - \frac{\partial T}{\partial\varphi_{2}} = - \frac{\partial П}{\partial\varphi_{2}} + Q_{2}$

Бірінші есептегі қарастырылған еркін тербелістердің кинетикалық және потенциалдық энергияларын аламыз.

$T = \frac{1}{2}\left( a_{11}*\dot{\varphi_{1} + 2a_{12}\dot{\varphi_{1}\dot{\varphi_{2} + a_{22}\dot{\varphi_{22}^{2 \right)$

$П = \frac{1}{2}\left( с_{11}\varphi_{1}^{2} + 2с_{2}\varphi_{1}\varphi_{2} + с_{22}\varphi_{2}^{2} \right)$

$а_{11} = m_{1} = 2, \ \ a_{12} = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ a_{22} = 1, 667\$

$c_{11} = 2250\ \ \ \ \ \ \ c_{12} = - 433\ \ \ \ \ c_{22} = 3750$

$a_{ij} - инерция\ коэффиценттері, \ c_{ij} - қаттылық\ коэффиценті$

Бірінші есебімде қарастырылған еркін тербелістер жиіліктері және таралу коэффиценті мына мәнге ие

$к_{1} = 23с^{- 1\ \ \ \ \ }\ \ \ \ \ \ \ \ к_{2} = 31с^{- 1}\ \ \ \ \ \ \ \ \ \ \ \ \mu_{1} = 0, 27\ \ \ \ \ \ \ \ \ \ \mu_{2} = - 3, 7$

Енді қозғалыс тудырушы $Q_{\varphi_{1\ \ \ }}\ \ \ және\ Q_{\varphi_{2}}\ \ \ \ \ \ моментімен\ \$ байланысты жалпы күштерді табамын

$Q_{\varphi_{1}} = \frac{\delta A_{M_{\varphi_{1{\delta\varphi_{1}}$

$Q_{\varphi_{2}} = \frac{\delta A_{M_{\varphi_{2{\delta\varphi_{2}}$

$Q_{\varphi_{1}} - \varphi_{2}$ =const кезінде, $\varphi_{1}$ жалпы координатасының қарапайым өсімінен пайда болған қозғалыс тудырушы күштің элементар жұмысы.

$Q_{\varphi_{1}} - \varphi_{1}$ =const кезінде, $\varphi_{2}$ жалпы координатасының қарапайым өсімінен пайда болған қозғалыс тудырушы күштің элементар жұмысы.

Егер t=0 кезіндегі қозғалыс тудырушы моменттің бағытын оң деп қабылдап, және ол $\varphi_{2}$ бұрыштың оң санақ бағытына сәйкес болса келесі теңдеуді аламыз.

$Q_{\varphi_{1}}$ =0

$Q_{\varphi_{2}}$ = $M_{0}$ cospt демек, $\varphi_{1}$ және $\varphi_{2}$ жалпыланған координаттарындағы еріксіз тербелістер жүйесін сипаттайтын (№) дифференциалдық теңдеу келесі түрге ие.