Қатты денелер статикасы: Пуансо теоремасы, кеңістік және жазық күштер жүйелерінің тепе-теңдік шарттары және ауырлық орталығы


9. Күштер жүйесін берілген центрге келтіру туралы статиканың негізгі (Пуансо) теоремасы.
Пуансо теоремасы: Қатты денеге әсер етуші күштердің жазық жүйесі, жалпылама алғанда, осы күштердің геометриялық жиындығына тең, аталаған күштердің әсер ету жиындығына кез келген бір О нүктесіне түсірілген жалғыз күшке және алгебралық моменті әсер етуші О нүктесі арқылы алынған моменттердің жиынына тең қос күшке эквивалент болады.
Дәлелдеу: Қатты денеге күштер жүйесі түсірілген делік. Осы күштерді О нүктесіндегі бір күшке келтіру үшін күшті өзіне паралель тасымалдау туралы лемманы әрбір күшке жеке қолданамыз.
=
= = ( ) = ×
Кеңістіктегі кез келген бағыттағы күштер жүйесін бір нүктеге келтіргенде, ол жалғыз күшке - бас вектроға, және жалғыз қос күшке -бас моментке келтіріледі.
Кеңістік күштер жүйесі үшін және бағыттары кез келген бағытта болса, жазық күштері үшін жазықтық бетінде, ал оған перпендикуляр орналасады.
- күштер жүйесінің бас векторы деп аталады.
- күштер жүйесінің О нүктесі арқылы алынған бас моменті деп аталады.
10. Кез келген кеңістік күштер жүйесі тепе-теңдігінің шарттары.
Қатта денеге әсер етуші бас вектор мен бас момент нөлге тең болатын жағдайды қарастырайық.
= =0,
(1)
=∑ ( ) =0
Қатты денеге әсер етуші кез келген кеңістік күштер жүйесі тепе-теңдік шартта болуы үшін (1) формулада келтірілген теңдіктердің орындалуы қажет және жеткілікті. Қорыта айтқанда, еркін қатта денеге әсер етуші кез келген кеңістік күштер жүйесі тепе-теңдік шартта болу үшін, осы күштер жүйесінің бас векторы мен бас моменті нөлге тең болуы қажет және жеткілікті болып табылады.
Тәжірбиедегі есептерді шғару үшін тепе-теңдік шарттарын скаляр түрінде жазу керек. Ол үшін бас вектордың координата осьтеріне проекцияларын және бас моменттің осы осьтердегі проекцияларын алып, алты теңдеуден тұратын теңдеулер жүйесін аламыз. Олар:
∑ =0, ∑ =0, ∑ =0,
( ) =0, ( ) =0, ( ) =0.
Сонымен, еркін қатты денеге әсер етуші кез келген кеңістіктік күштер жүйесі тепе-теідік шартта болуы үшін әсер етуші барлық күштердің үш координаттар осьтердегі проекцияларының қосындысына және осы осьтерге қатысты моменттердің проекцияларының алгебралық қосындысының нөлге тең болуы қажет және жеткәләктә болып табылады.
11. Кез келген жазық күштер жүйесі тепе-теңдігі шарттарының үш түрі.
Кез келген жазық күштер жүйесінің тепе-теңдік шарттарының бірінші түрі :күштердің екі координат өсіне проекцияларының қосындылары және кез келген центрге қатысты күштердің алгебралық моменттерінің қосындысы нөлге тең болуы қажетті де жеткілікті
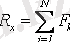 ,
,
 ,
,
 .
.
Екінші түрі
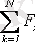 ,
,
 ,
,
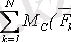 ,
,
мұнда
 түзуі
түзуі
 өсіне перпендикуляр емес болу керек.
өсіне перпендикуляр емес болу керек.
Үшінші түрі
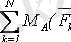 ,
,
 ,
,
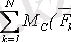
мұнда А, В, С бір түзудің бойында жатпау керек.
Жазық параллель күштер жүйесі үшін тепе-теңдік шарттары келесідей
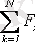 ,
,

(мұнда Ox өсі күштерге перпендикуляр болмау керек) немесе
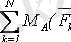 ,
,
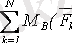 ,
,
мұнда А мен В нүктелерінен өтетін түзу күштерге параллель болмау керек.
12. Қатты дененің ауырлық центрі.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz