Дифференциалдық теңдеулерді графикалық шешудің изоклин әдісі


Қазақстан Республикасының Білім және Ғылым Министрлігі
Л. Н. Гумилев атындағы Еуразия Ұлттық университеті
Іргелі математика кафедрасы
Мақала
Дифференциалдық теңдеулерді шешудегі изоклин әдісі
Орындаған: М-41 тобының студенті Ғаниева А. Д.
Жетекші: ф. -м. ғ. к., профессор Тлеулесова А. Б.
Нұр-Сұлтан, 2020
Дифференциалдық теңдеулерді шешудегі изоклин әдісі.
Ғаниева А. Д.
Кілт сөздер: дифференциалдық теңдеу, шешімі, интегралдық қисық, изоклин.
Аңдатпа: Мақалада дифференциалдық теңдеуді шешудің графикалық әдісі- изоклин әдісі, даму тарихы қарастырылады. Осы әдісті қарастырған математиктердің еңбектері зерттеледі.
E-mail: akzhan. ganieva@bk. ru
Дифференциалдық теңдеулер - әр түрлі ғылыми-техникалық мәселелерді шешу үшін кеңінен қолданылатын маңызды теңдеулер болып табылады. Дифференциалдық теңдеулерді, механика, астрономия, физиканың қолданбалы мәселелерінің тікелей әсерінен қалыптасқан әдіс - біртіндеп жуықтау әдісі арқылы шешу қазір ерекше қолданысқа ие.
Дифференциалдық теңдеулерді шешудің біртіндеп жуықтау әдісі:
-шешімді аналитикалық өрнек түріндегі ұсынатын - аналитикалық әдістер;
-қажетті шешімді тек жеке нүктелерде, яғни кесте түрінде табуға мүмкіндік беретін сандық әдістер;
- геометриялық құрылымдарды пайдаланатын - графикалық әдістер
болып бөлінеді. Шешудің графикалық әдістеріне
кеңінен қолданылатын изоклин әдісін жатқызуға болады.
Бірінші ретті дифференциалдық теңдеудің графикалық шешімі туралы бірінші рет 1694 жылы И. Бернуллидің «Acta Eruditorum» басылымында «Общий способ построения всех дифференциальных уравнений первого порядка» мақаласында жарияланған[4] .
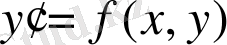 Изоклин әдісі(бірінші ретті теңдеулер үшін) .
Изоклин әдісі(бірінші ретті теңдеулер үшін) .
(1) дифференциалдық теңдеудің геометриялық мағынасын қарастырайық. Айталық
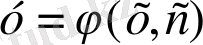 осы теңдеудің жалпы шешімі болсын. Бұл шешім
Оху
жазықтығында интегралдық қисықтар тобын анықтайды. (1) теңдеу әрбір
М(х, у)
нүктеде туынды мәнін анықтайды, демек осы нүкте арқылы өтетін интегралдық қисыққа жүргізілген жанаманың бұрыштық коэффициентін анықтайды. Сонымен, (1) дифференциалдық теңдеу бағыттар жиынын береді, немесе, әдетте, бағыттар өрісін анықтайды деп атайды.
осы теңдеудің жалпы шешімі болсын. Бұл шешім
Оху
жазықтығында интегралдық қисықтар тобын анықтайды. (1) теңдеу әрбір
М(х, у)
нүктеде туынды мәнін анықтайды, демек осы нүкте арқылы өтетін интегралдық қисыққа жүргізілген жанаманың бұрыштық коэффициентін анықтайды. Сонымен, (1) дифференциалдық теңдеу бағыттар жиынын береді, немесе, әдетте, бағыттар өрісін анықтайды деп атайды.
Демек, дифференциалдық теңдеуді интегралдау есебі геометриялық тұрғыдан қарағанда жанама бағыты сол нүктеге сәйкес келетін өріс бағытымен дәл келетіндей қисықтарды табуда екен.
(1) дифференциалдық теңдеу үшін
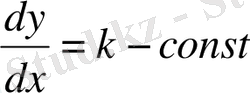 қатынасы орындалатын геометриялық нүктелерді берілген теңдеудің
изоклині
деп атайды[3] .
С
-ның әртүрлі мәндерінде изоклиндердің әртүрін аламыз.
k
-ға сәйкес келетін изоклин теңдеуі
қатынасы орындалатын геометриялық нүктелерді берілген теңдеудің
изоклині
деп атайды[3] .
С
-ның әртүрлі мәндерінде изоклиндердің әртүрін аламыз.
k
-ға сәйкес келетін изоклин теңдеуі
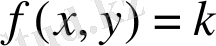 болады. Изоклин топтарын құрып, жуықтап интегралдық қисықтар тобын құруға болады. Берілген изоклинді қиып өтетін барлық интегралдық қисықтар абцисса осімен бірдей бұрыштар жасайды.
болады. Изоклин топтарын құрып, жуықтап интегралдық қисықтар тобын құруға болады. Берілген изоклинді қиып өтетін барлық интегралдық қисықтар абцисса осімен бірдей бұрыштар жасайды.
1-мысал[1]
.
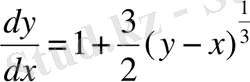 теңдеуінің ерекше шешімдерін анықтап, интегралдық қисықтарын тұрғызыңыз.
теңдеуінің ерекше шешімдерін анықтап, интегралдық қисықтарын тұрғызыңыз.
Шешуі
:
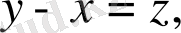 алмастыруын енгізіп, келесі теңдеуді аламыз:
алмастыруын енгізіп, келесі теңдеуді аламыз:
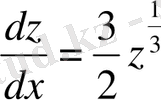 (2)
(2)
z=0 кезде (2) теңдеу Липшиц шартын қанағаттандырмайды[3] .
z=0 соңғы теңдеудің шешімі болғандықтан ерекше шешім болуы мүмкін. (2) теңдеудің басқа да шешімдерін қарастырайық:
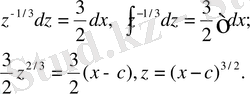
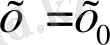 болғанда
болғанда
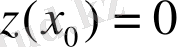 шартын (2) теңдедің кем дегенде екі шешімі қанағаттандырады:
шартын (2) теңдедің кем дегенде екі шешімі қанағаттандырады:
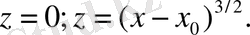
Сондықтан z=0 - (2) теңдеудің ерекше шешімі.
Басында берілген алмастыруды ескерсек, бастапқы теңдеу үшін у=х
ерекше шешім болып табылатынын байқаймыз.
Қалған шешімдерді мына формула арқылы есептейміз:
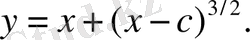

2-мысал
:
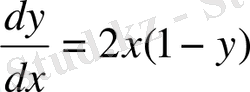 теңдеуінің интегралдық қисықтарын изоклиндердің көмегімен салыңыздар.
теңдеуінің интегралдық қисықтарын изоклиндердің көмегімен салыңыздар.
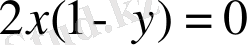 Шешуі. Берілген теңдеудің изоклиндері
Шешуі. Берілген теңдеудің изоклиндері
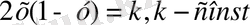 , теңдеуден анықталады.
k=0
болғанда, болады да
х=0
және
у=1
екі түзуін, сонымен қатар
, теңдеуден анықталады.
k=0
болғанда, болады да
х=0
және
у=1
екі түзуін, сонымен қатар
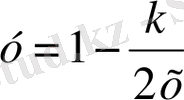 гиперболалар тобын береді.
у=1
түзуі дифференциалдық теңдеудің шешімі болғандықтан интегралдық қисық болады. Ординаталар осімен интегралдық қисықтар тік бұрыш жасайды, демек олардың жанамасы абцисса осіне параллель болады. Бұл
х=0
қисығының нүктелері интегралдық қисықтар үшін кризистік нүктелер болатынын көрсетеді. Кризистік нүктелер характерін анықтау үшін
у=у(х)
функциясының екінші ретті туындысын табамыз.
гиперболалар тобын береді.
у=1
түзуі дифференциалдық теңдеудің шешімі болғандықтан интегралдық қисық болады. Ординаталар осімен интегралдық қисықтар тік бұрыш жасайды, демек олардың жанамасы абцисса осіне параллель болады. Бұл
х=0
қисығының нүктелері интегралдық қисықтар үшін кризистік нүктелер болатынын көрсетеді. Кризистік нүктелер характерін анықтау үшін
у=у(х)
функциясының екінші ретті туындысын табамыз.
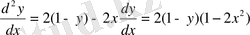
Демек, ординаталар осінің
у>1
болатындығы ординат осінің нүктелері интегралдық қисықтың минимум нүктелері болады. Сонымен қатар
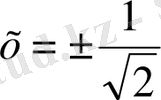 нүктелер интегралдық қисықтар тобының иілу нүктелері болады. Ары қарай,
х=0
және
у=1
түзулер координаталар жазықтығын әрқайсысында
нүктелер интегралдық қисықтар тобының иілу нүктелері болады. Ары қарай,
х=0
және
у=1
түзулер координаталар жазықтығын әрқайсысында
 туындысының таңбасы бірдей болатын төрт бөлікке бөледі. Ендеше,
у>1
болғанда интегралдық қисықтар
х=0
түзуін қиып өтіп
у(х)
функциясының өсу облысынан оның кему облысына өтеді. Тағы да
k=1
және
k=-1
болғандағы екі изоклинді қарастырамыз:
туындысының таңбасы бірдей болатын төрт бөлікке бөледі. Ендеше,
у>1
болғанда интегралдық қисықтар
х=0
түзуін қиып өтіп
у(х)
функциясының өсу облысынан оның кему облысына өтеді. Тағы да
k=1
және
k=-1
болғандағы екі изоклинді қарастырамыз:
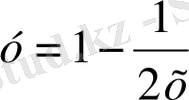 және
және
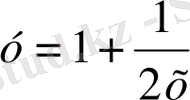
Осы изоклиндермен қиылысу нүктелеріндегі интегралдық қисықтарға жүргізілген жанамалар абцисса осімен сәйкес
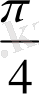 және
және
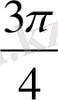 бұрыштар жасайды.
бұрыштар жасайды.
Изоклин әдісі (екінші ретті теңдеулер үшін) .
Изоклин әдісі кейбір, 1-ретті теңдеуге келтірілетін, 2-ші ретті теңдеулерді де шешуге қолданылады.
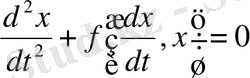
(1)
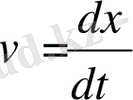
Жаңа айнымалы енгіземіз:
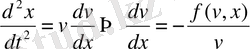
Онда (2)
енді теңдеу 1-реттіге келді, изоклин әдісімен шешуге болады.
х -қандай да бір жүйенің нүктесінің орын ауыстыруы;
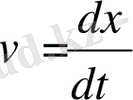
оның жылдамдығы болсын.
x, v айнымалыларының жазықтығы фазалық жазықтық деп аталады.
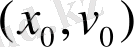 Осылай (2) теңдеу жылдамдықты орын ауыстыру функциясы ретінде анықтайды. (2) теңдеу үшін изоклин өрісін құра отырып, бастапқы нүктелер берілген болса интегралдық қисықты сыза аламыз.
v=v(x)
бұл тәуелділікті бейнелейтін жазықтықтағы қисықтар фазалық траектория деп аталады.
Осылай (2) теңдеу жылдамдықты орын ауыстыру функциясы ретінде анықтайды. (2) теңдеу үшін изоклин өрісін құра отырып, бастапқы нүктелер берілген болса интегралдық қисықты сыза аламыз.
v=v(x)
бұл тәуелділікті бейнелейтін жазықтықтағы қисықтар фазалық траектория деп аталады.
Мысалы:
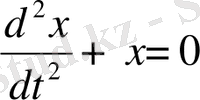
(3) теңдеу үшін фазалық жазықтықта траекторияларын
құрыңыз.
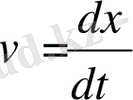
Шешуі: деп ұйғарайық.
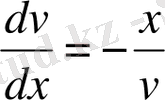
Онда (3) теңдеудің түрі: (4)
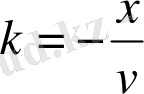
(4) теңдеу үшін изоклин теңдеуі:
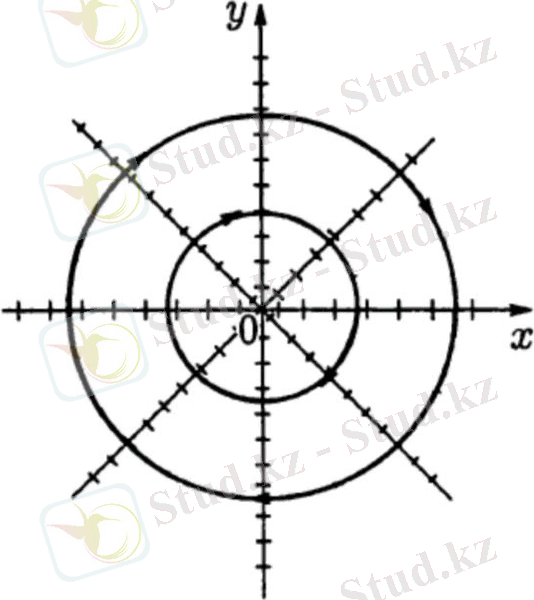
k -ның әртүрлі мәніне сәйкес изоклиндерді сыза отырып, фазалық траекторияларды (0; 0)
нүктесінде центрі орналасқан шеңберлер екенін байқаймыз.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz