Дифференциалдық есептеу элементтері жайлы қысқаша тарихи мағлұматтар

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 26 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
Мектеп аты

Ғылыми жоба тақырыбы: ТУЫНДЫНЫ ПОПУЛЯЦИЯ САНЫН ЕСЕПТЕУДЕ ҚОЛДАНУ

Жоба авторы:
Жоба жетекшісі:
Ғылыми жетекші:

2021

М А З М Ұ Н Ы
КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 3

ТЕОРИЯЛЫҚ БӨЛІМ
1.1. Дифференциалдық есептеу элементтері жайлы қысқаша тарихи мағлұматтар ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 5
ПРАКТИКАЛЫҚ БӨЛІМ
Екі популяцияның тіршілік үшін күресін сипаттайтын В. Вольтерраның модельдері ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 13
Биологиялық популяция мөлшерінің динамикасы туралы есеп : Мальтус пен Ферхюльст модельдері ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ...24

Қорытынды ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 29
Пайдаланылған әдебиеттер тізімі ... ... ... ... ... ... ... . ... ... ... ... ..31

КІРІСПЕ

Зерттеу тақырыбының көкейкестігі. Зерттеу жұмысында қарастырылған мәселенің көкейкестігі қазіргі ғылым мен техниканы және экономиканы көтерудің күрделі мәселелерін шешу білім берудің жаңашылдық міндеті қоғамдық қатынастар мен құндылықтар жүйесіндегі өзгеріс талаптарына сәйкес мектептегі білім беру сапасын арттыру болып табылады.
Зерттеу мақсаты: Туындының жан-жақтылығын зерттеу, мысалдар келтіру, популяция санын есптеуде қолданылуын түсіндіру.

Зерттеудің міндеттері:
Зерттеудің проблемасын шешу, болжамның дұрыстығына көз жеткізу және мақсатқа жету үшін келесі мәселелер орындалады:
осы тақырып бойынша бар ғылыми-зерттеу әдебиеттерді зерттеу;
заманауи оқу құралдарына осы тақырыптың баяндалуына логикалық талдау жүргізу;
алынған мәліметтерді жалпылау және жүйелеу;
жасалынған әдістемені пайдаланудың тиімділігін тәжірибеде тексеру;

Зерттеу әдістері:
Жұмыстың мақсатына жету, болжамды тексеру және жоғарыда қойылған мәселелерді шешу үшін келесі әдістер пайдаланылады:
гипотеза жасау, тексеру
мәліметтерді іздеу, жинақтау талдау;
әр түрлі ғылыми зерттеу жұмыстарын салыстырмалы талдау;
индуктивті және дедуктивті қорытындылау әдісі
бақылау және бағалау;
уақытты үнемдеу мақсатында социометриялық әдісті де қолдану.

Зерттеу объектісі: 10-сынып алгебра және анализ бастамаларын оқыту үрдісі.
Зерттеу пәні: туынды мен туындының көмегімен функцияны зерттеуді оқыту.
Зерттеудің теориялық және практикалық маңыздылығы:
Жұмыста келтірілген теориялық және дидактикалық материалдар, сабақтың жоспар-конспектілері, ұсынылған әдістемелік жолдары 10-11 жаратылыстану-математика бағытындағы сыныптарда алгебра және анализ бастамалары курсында Туынды және оның қолданылуы тақырыбын тиімді оқытуға математик студенттер мен мектеп математика мұғалімдеріне көмегін тигізеді
Ғылыми жоба кіріспеден, 2 тараудан, қорытынды және қолданылған әдебиеттерден тұрады.
Ғылыми жоба кіріспеден, 2 тараудан, қорытынды және қолданылған әдебиеттерден тұрады.

Теориялық БӨЛІМ
Дифференциалдық есептеу элементтері жайлы қысқаша тарихи мағлұматтар

Ғылыми ұғымдарды саналы да, терең меңгергенде ғана оқушылардың қоршаған дүниені толық, бүтін қабылдауларына жағдай туғызуға болады, жан-жақты өз бетінше және белсенді ойлайтын адам етіп қалыптастыруға болады.
Дүние таным өкілдері ұғым-мидың, материяның жоғарғы жемісі деп атап көрсеткен. Әр ғылым саласы бойынша пайда болған ұғым өзінің даму кезеңдерінде өзгеріссіз қалып қоймайды. Заттар мен құбылыстардың жаңа қасиеттер мен белгілерге ие болуы нәтижесінде ұғым мазмұны қоюланып, молая түседі, көлемі кеңиді, олардың қатыстары мен байланыстары толығырақ айқындалады.
Шек ұғымы - өте терең ұғым. Шек ұғымы математикада кеңінен ХVІІ ғасырдан бастап қолданылса да, оның дәл анықтамасы ХІХ ғасырда ғана (дәл айтқанда, 1821 жылы) берілген еді. Бұның бір себебі әуелі тәуелсіз айнымалыны, сосын тәуелді айнымалыны қарастыру қажет деп жаңылыс ойлау болды.
Lim белгіленуі - латынның limes (меже, шекара) деген сөзінің қысқарған түрі: мысалы, -ті кеміте отырып, біз мәнін шекарасына ұмтыламыз. Шек терминін Ньютон енгізген. Бұл ұғым интуитивті деңгейде XVII ғасырдың екінші жартысында ағылшын физиктерінің, математик және атроном И.Ньютонның, XVIІІ ғасырда неміс және орыс математиктерінің, Л.Эйлердің, француз математигі Жозеф Луи Лагранждың еңбектерінде кездесті. Алғаш рет шек ұғымының қатаң анықтамасын берген 1810 жылы чеш ғалымы математик, философ Бернард Больцано (1781-1848) және 1821 жылы Огустен Коши (1789-1857) берді. Қазіргі кезде шектер теориясы экономикалық есептеулерде, қаржылық мәселелерде, сондай-ақ банк жүйесінде де үлкен сұранысқа ие болап, қарқынды қолданылуда. Шекті қолдану арқылы кез келген үзіліссіз процестерді есептеуге болады.
Туындылар және олардың функцияларды зерттеуде қолданылуы қарастырылатын математиканың бөлімі дифференциалдық есептеу деп аталады. Айырманы көрсететін түріндегі өсімше туындылармен жұмыс істегенде елеулі орын алады. Сондықтан да жаңа есептеу cakculis differentials (айырмаларды есептеу деп аударылады) атауында латынша differentia (айырма) түбірінің көрініс табуы орынды. Бұл атау ХVII ғасырдың аяғында, яғни жаңа әдіс дүниеге келгенде пайда болады.
Туынды термині derive деген француз сөзінің қазақша сөзбе-сөз аудармасы, оны 1797 жылы Ж.Лагранж (1736-1813) енгізген, қазіргі кездегі , белгілеулерін де сол енгізген-ді. Бұл атау мынадай ұғымның мағынасын ашады: функциясы -тен шығады, -тің туындысы болып табылады. И.Ньютон функцияның туындысын флюксия деп, ал функцияның өзін флюента деп атаған. Г.Лейбниц дифференциалдық қатынас туралы айтқан және туындыны түрінде белгілеген. Бұл белгілеу қазіргі әдебиетте де жиі кездеседі. Лейбниц символын функциясының дифференциалын белгілеу үшін таңдап алған. функциясының дифференциалы - туындысының өсімшесіне көбейтіндісі,яғни белгілеуін -пен алмастырып, оны былай жазуға болады: , осыдан . Олар алғаш рет жаңа есептеудің негізгі амалдары дифференциалдау мен интегралдауды жалпы түрде қарастырып, олардың өзара байланысын тағайындады ( Ньютон- Лейбниц формуласы). Алайда Ньютон мен Лейбниц бұл мәселеге қатысы әр түрлі көзқараста болды. Ньютон үшін бастапқы ұғымдар- механикалық есептерден келген флюента (айнымалы шама) және оның флюксиясы (айнымалы шаманың өзгеру жылдамдығы). Флюксияларды және флюенталар бойынша флюнсиялар арасындағы қатыстарды ( дифференциалдау және дифференциалдық теңдеулер құру) табуды көздеген тура есепке Ньютон флюнсиялар арасындағы қатыстар бойынша флюенталарды табу жайлы кері есепті, былайша айтқанда дифференциалдық теңдеулерді интегралдаудың жалпы есебін қарсы қойды. Лейбниц болса әсіресе шекті шамалар алгебрасынан шексіз аз шамалар алгебрасына көшуге көп көңіл болды, ол интегралды ең әуелі саны шексіз көп шексіз аз шамалардың қосындысы ретінде, ал дифференциалдық есептеулердің негізгі ұғымын айнымалы шамалардың шексіз өсімшесі түрінде қарастырды. Бұл саладағы идеяларды Я. Бернулли, И. Бернулли, француз математигі Г. Лопиталь т.б. одан әрі дамытты. Аналитикалық геометриядан басқа алгебра мен анализге тығыз байланысты дифференциалдық геометрия да дамыды. Дифференциалдың геометриялық мағынасы 1-суреттен анық көрінеді: мұнда , l түзуі - графикке жүргізілген жанама.

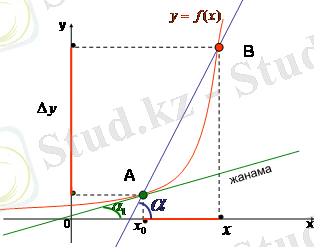
1-сурет.

Дифференциалдық есептеулерде қабылданған терминология туралы әңгімені шек және шексіз аз ұғымдары толықтыра түседі. Шек туралы төменде егжей-тегжейлі айтылады. Мысалы, туынды барлық нұсқауларда шек ретінде анықталады. Жоғарыда қабылданған жағдайда деп жазудың орнына түрінде жазады.
-тен функциясы шексіз аз шаманың мысалы бола алады, өйткені жағдайда . Жалпы, егер болса, -шексіз аз деп атайды. Математикалық анализде шексіз аздар маңызды орынға ие. Сондықтан, оны көбінесе шексіз аздар анализі деп атайды.
Ақырында, экстремум сөзі латынша extremum (шеткі) дегеннен шыққанын айта кетейік. Қазақша maximum - ең үлкен, minimum - ең кіші деп аударылады.
Дифференциалдық есептеуді Ньютон мен Лейбниц біршама беріректе, XVII ғасырдың соңында құрды. Таңқаларлық бір нәрсе, бұдан көп бұрын Архимед аса күрделі спираль сияқты қисыққа жанама жүргізу есебін шығарған (ол мұнда шекке көшуді қолданған), сонымен бірге функциясының максимумын таба білген.
Жанама ұғымы (ол, өздерің білесіңдер, туынды ұғымымен байланысты) итальян математигі Н.Тарталья (1500-1557ж) еңбектерінде ауық-ауық ұшырасып қалады, мұнда жанама зеңбіректің оқты барынша алысқы атуға көмектесетін көлбеулік бұрышы жөніндегі мәселені оқып үйрену барысында айтылады. И.Кеплер радиусы берілген шарға іштей сызылған параллелипипедтің ең үлкен көлемі туралы есепті шығару барысында жанаманы қарастырған.
XVII ғасырда Г.Галилейдің қозғалыс туралы ілімі негізінде туындының кинематикалық концепциясы қарыштап өркендеді. Әр түрлі есептерді шығаруға қолданылған алуан түрлі варианттардың баяндалуы Р.Декартта, француз математигі Робервальде (1602-1675), ағылшын ғалымы Д.Грегориде (1638-1675), И.Барроу (1630-1677) мен И.Ньютон еңбектерінде кездеседі. Жанама мен нормальды (жанамаға перпендикуляр және жанасу нүктесінде жүргізілген түзу осылай аталады) қарастыруға Декарт линзалардың оптикалық қасиеттерін зерттеу барысында келді. Ол аналитикалық геометрия әдістерінің және өзі ойлап тапқа. Анықталмаған коэффициенттер әдісінің көмегімен бірқатар қисықтарға, соның ішінде эллипске нормальдар салу туралы есепті шығара білді.
1629 жылы П.Ферма көпмүшелердің экстремумдарын табу ережелерін ұсынды. Айта кететін елеулі нәрсе, Ферма осы ережелерді қорытып шығарғанда, максимум мен минимумның қарапайым дифференциалдық шартын біле отырып, шекке көшуді қауырт қолданды.
Туындылар туралы ғылымды жүйелі дамытқан Лейбниц пен Ньютон болды. Олар анализдің негізгі екі мәселесін тұжырымдады:
Жүретін жолдың тұрақты (яғни кез келген уақыт мезетіндегі) ұзындығы берілген,көрсетілген уақыт ішіндегі қозғалыс жылдамдығын табу керек.
Қозғалыс жылдамдығы тұрақты берілген; көрсетілген уақыт ішінде жүрілген жолдың ұзындығын табу керек.
Бірінші мәселе дифференциалдық есептеудің даму бағдарламасын береді, оның элементтерімен сендер осы тарауда танысқансыңдар. Екіншісі интегралдық есептеуге жатады.
Ньютон механика есептерін негізге алса (Ньютондық анализ ньютондық классикалық механикамен қатар жасалған-ды), Лейбництің артықшылығы ол геометрия есептерін негіз етіп алды.
Анализ идеяларының одан кейінге дамулары туралы айтқанда (ол идеялар тез тарап кетті және өзіне көптеген ізбасарлар тапты) Лейбництің шәкірттері - ағайынды Якоб және Иоганн Бернуллилердің есімдерін алдымен атаған жөн.
А.Лопиталь (1661-1704) И.Бернуллиден дәріс алған, ол 1696 жылдың өзінде дифференциалдық есептеудің алғашқы курсы Қисық сызықтарды зерттеуге арналған шексіз аздар анализін баспадан шығарып үлгерді,бұл жаңа әдістердің тарауына септігін тигізді.
Бұл салада ірі нәтижелерге жеткен Лагранж еді, оның еңбектері анализ негіздерінің мән-мағынасын түсіндіруде зор роль атқарады.
Математиканың басқа да көптеген бөлімдері сиқты, математикалық анализдің дамуына да Л.Эйлердің және К.Ф.Гаусстың (1777-1855) теңдесі жоқ үлестері бар.
XVIIІ ғасырдағы және одан кейінгі жасалған жаңалықтар туралы қысқа мақалада әңгімелеп шығу мүмкін емес. Әңгіме функцияларды дәрежелік қатарларға жіктеу, яғни функцияларды қосылғыштардың саны шектеусіз көпмүшелер түрінде көрсету жөнінде болып отыр. Шектеусіз қосындылардың (сандық қатар) мысалы сендерге таныс, мысалы шектеусіз периодты ондық бөлшектерді қосылғыштарнының саны шектеусіз қосынды түрінде көрсету. Сандық және функциялық қатарлармен Ньютон ғана емес, одан бұрынғылар да шұғылданған болатын, сондықтан да мынадай тамша қатыс үшін

(мұндағы - f функциясын нүктесінде n рет дифференциалдаудан шыққан мән, ал )қабылданған Тейлор формуласын атамай кету дұрыс болмас еді. Туындылар формулаларын біле отырып, мысалы функцияларын Тейлор қатарына жіктей аласыздар.
Кейбір жағдайларда, қосылғыштардың шектеусіз санын ескермей тастап кетіп, көпмүшелермен берілген функциялар жап-жақсы жуықтау беретін формула шығарып алуға болады екен.
2) Шығарылатын есептер шеңберін кеңейтуге мүмкіндік беретін қуатты жаңа әдістердің пайда болуынан туған ынта XVIIІ ғасырда анализдің қарқынды дамуына сбепші болады. Алайда осы ғасырдың соңында дифференциалдық және интегралдық есептеулерді жасауда аса өткін проблемалар пайда болды.
Негізгі қиыншылық мынада еді: шек, үздіксіздік, нақты сан сияқты терминдердің дәл анықтамалары болмады, осыған сәйкес пайымдауларды логикалық жағынан олқылықтар, кейде қателіктер де болды. Бұған тән мысал - үздіксіздік қасиеті. Эйлер, Лагранж тіпті Фурье (ол ХІХ ғасырдың басында жұмыс істеген) өзінің анықталу облысында бір ғана аналтикалық өрнекпен берілетін функцияны үздіксіз деп атады.
Осы жағдайлардан жаңа математика грек математиктерінің классикалық үлгісінде тәрбиеленген ғалымдар үшін үйреншікті қатаңдық стандартына сай келе алмады. Математиктерге аса қажетті и нтуиция математикалық ғылымның бөлінбейтін сипттамасы болып табылатын логикадан едәуір озып кетті. Ньютон, Лейбниц, Эйлер сияқты алыптардың данышпандық интуициясы оларды қателесуден сақтап қалды. Бірақ, қалайда берік логикалық негіз қажет болды.
XVIIІ ғасырға қатысты ерекше екі пікір болды. Белгілі математик М.Ролль жаңа есептеу данышпандық қателердің жиынтығы деп жазды. Ал француздың ұлы ойшысы Вольтер бұл есептеу дегеніміз есептеп шығаруға және бар жоғын дәлелдеуге болмайтын затты дәл өлшеу өнері екенін ескерткен-ді.
Анализдің берік іргетасын қалауға шешуші қадамды өткен ғасырдың
20-жылдарында француз ғалымы О.Коши жасаған еді, ол функция мен тізбек шектерінің дәл анықтамаларын ұсынды және соларды негіз ете отырып, анализдің көптеген іргелі теоремаларын дәлелдеді. Бұдан біршама бұрын чех математигі Б.Больцано шек пен үздіксіздіктің анықтамасын, басқа да, бірқатар тамаша нәтижелерге, соның ішінде аралықта үздіксіз, бірақ оның ешбір нүктесінде туындысы болмайтын функцияның мысалы бар екеніне қол жеткізген еді, бірақ оның жұмыстары көп кейін белгілі болды.
Функция шегінің Коши берген анықтамасы былай тұжырымдалады: Егер кез келген саны үшін нүктесінің аймағы табылып, осы аймақтағы әрбір үшін

теңсіздігі орындалса, онда А санын функциясының нүктесіндегі шегі деп атайды. Оны былай жазады: және оны х а - ға ұмтылғандағы функциясының шегі А-ға тең деп оқиды.
Сонымен, егер болса, онда функциясы нүктесінде анықталуы міндетті емес. Жалпы егер мәні анықталған болса да, А саны мен мәндері бір-біріне байланысты емес. Кейбір жағдайларды , яғни теңдігі орындалуы мүмкін. Ал кейбір жағдайларда теңсіздігі орындалуы да мүмкін.
Осы анықтамаға сүйеніп, функцияның нүктедегі үздіксіздігіне анықтама беру қиын емес: егер болса, онда f функциясын нүктесінде үздіксіз болады.
Тізбек шегінің анықтамасы былай тұжырымдалады: Егер кез келген саны үшін саны табылып, теңсіздігін қанағаттандыратын әрбір х үшін
(2)
теңсіздігі орындалса, онда функциясының нүктесіндегі туындысы болады деп есептейміз.
Коши шектер туралы мынадай теоремаларды дәлелденген, оларды біз туындыларды есептеген кезде пайдаланғамыз (оларды шекке көшу ережелері деп атаған едік).
Егер limx--af(x) және limx--ag(x) шектері бар болса, онда limx--a[f(x)+-g(x)] шегі де бар болады және мына теңдік орындалады:
limx--a[fx+-g(x)]=limx--afx+-limx --agx
Бұл теорема қосылғыштар саны шектеулі болған жағдай үшін де орындалады.
Егер limx--af(x) және limx--ag(x) шектері бар болса, онда limx--a[f(x)∙g(x)] шегі де бар болады және мына теңдік орындалады:
limx--a[fx∙g(x)]=limx--afx∙limx-- agx

Егер limx--af(x) және limx--ag(x)!=0 шектері бар болса, онда limx--af(x)g(x) шегі де бар болады және limx--af(x)g(x)=limx--af(x)limx-- ag(x) теңдігі орындалады.
Кошише (көбінесе эпсилон-дельта тілінде деп атайды).
X жиынында анықталған f функциясы мен a нақты саны берілсін.
Егер белгілі бір b нақты саны мен кез келген ε оң саны үшін f функциясының анықталу жиынында жааттын және
0x-aδ ε (1)
Теңсіздіктерін қанағаттандыратын барлық x сандары үшін fx-bε теңсіздігі орындалатын δ ε оң саны табылса, онда fx функциясының x a-ға ұмтылғанда нақты мәнді шегі бар және ол b санына тең дейді де limx--afx=b, fx--a⇒fx--b(x--a) немесе x--a⇒fx--b символдарымен белгілейді.

XVII ғасырда математиктердің көбінің ұраны мынадай болған: Алға қарай қозғала беріңдер, ал нәтижелердің дұрыстығына сенім өзінен-өзі келеді.

2.1. Екі популяцияның тіршілік үшін күресін сипаттайтын
В. Вольтерраның модельдері
Жыртқыштың (жолбарыс, қасқыр, бүркіт, акула) қорегі әдетте шөпқоректі жануар, майда құстар мен балықтар. Тіршілік үшін күресте арыстан шибөрінің қорегін тартып алады. Тіршілік үшін күресті қоршаған орта мен организм арасындағы күрделі қарым-қатынастардың жиынтығы деп түсінген дұрыс. Бір түр мен екінші түрдің арасындағы күресті түраралық күрес дейді. Ол жыртқыштық жағдайдағы бәсекелестік (қасқыр-түлкі) , паразиттік жағдайдағы бәсекелестік (ағаштар-лианалар) түрінде жүреді.
Жыртқыш пен оның жемтіктерінің Жер бетіне кең таралуын кейбір факторлар шектеп отырады. Мысалы, ақ аю үшін шектеуші фактор- температура, ақ тиін үшін - шырша, ал қасқыр үшін - қорек. Жыртқыштар мен жануарлардың басым көпшілігі консументтер (тұтынушылар) қатарына жатады және дайын органикалық затпен қоректенеді.
Кейбір организмдер өзінің популяциясын тұрақты ұстау үшін топтанып, үйір немесе колония құрып тіршілік етеді.Мысалы, бұғылар 200-300 бас табын құрып тіршілік етсе, қасқырлар 7-10, ақбөкендер 10-25.000 бас болып үйір құрайды екен. Мұндай топ құрау жануарлар дүниесінің бірігіп жауларынан қорғану, қорегін аулау сияқты қасиеттерінен туындайды.
Табиғатта популяциялардың сан мөлшерінің реттелу механизімінің бір формасы - популяция аралық реттелу. Бұл дегеніміз, биоценоздағы әртүрлі популяциялар бірін-бірі реттеуге тырысып, табиғаттағы жалпы тұрақты дамуды жүзеге асыруға ұмтылады деген сөз.
Табиғи жағдайларда популяциялар әдетте оқшауланып өмір сүре алмайды. Олардың бір-бірімен байланыстары өте тығыз және симбиоз, бәсекелестік, паразитизм, бір-бірін жою және т.б. формаларда жүретін болады. Биологтар осы байланыстарды тіршілік үшін күрес деп атайды. Егер кезкелген t уақыт мезетіндегі жемтік пен жыртқыштың мөлшерлерін N1 (t) және N2 (t) деп белгілесек , онда олардың өзгеру жылдамдықтары мынадай дифференциалдық теңдеулер жүйесімен сипатталатын болады:
(1)
пропорционалдық коэффициенттер , оң сандар .
жүйесі жыртқыш-жемтік моделінің тіршілік ету және өзара байланыс жағдайларын анықтайтын болады. Бастапқы шарттар

Әрине, алынған (1)-(2) түріндегі Коши есебінің кез-келген тіктөртбұрышта жалғыз шешімі табылады, өйткені (1) жүйесінің оң жақтарының N 1 мен N2 бойынша шектеулі туындылары бар болады. (1) жүйесінің шешімдерінің қасиеттерін зерттеу фазалық жазықтарында жүргізілетін болады. Бұл жүйеенің екі стационарлық шешімдері

жағдайында оңай табылады, олар мыналар:

Бірінші шешімінің біз үшін қажеттілігі жоқ. Екінші шешімді тиянақтап қарастыратын боламыз. Біз (1) жүйесінің шешімдері арқылы анықталатын траекториялардың мінез-қасиеттерін оның стационарлық шешімімен анықталатын фазалық жазықтық нүктесінің маңайында зерттейтін боламыз. Ол үшін (1) жүйесін шешуіміз қажет. Сол мақсатта 1-ші теңдеуді мүшелеп
-ге, ал 2- ні -ге көбейте отырып теңдеулерді бір-біріне қосамыз, сонда:

Онан әрі 1 - ші теңдеуді - ге мүшелеп бөліп - ге көбейтсек, ал 2 - ші теңдеуді мүшелеп -ге бөліп - ге көбейтіп , сөйтіп оларды қоссақ онда

яғни (3)
(4)
жүйесін аламыз , бірақ (3) пен (4) теңдеулерінің оң жақтары өзара тең. Сондықтан олардың сол жақтарын теңестіріп жазатын боламыз:
(5)
(5) теңдеуін мүшелеп интегралдасақ, алатынымыз

немесе

(6)
Соңғы алнған (6) қатысы (1) жүйесінің жалпы интегралы болады.
Әрине, С-нің әрбір нақты сандық мәні үшін бұл интегралға сәйкес жазықтығында контур (тұйықталған қисық) табылатын болады. С-нің басқа сандық мәнін алсақ , алғашқы контурды қимайтын басқа тұйықталған қисықты табамыз және табылған екі контурдың екеуі де өздерінің ішінде нүктесін қамтитын болады. Қорыта айтқанда , (6) интегралы нүктесін қамтитын контурлардың (траекториялардың) үйірін анықтайтын болады.

І контуры бойынан бастапқы (2) шарттарымен анықталған нүктесін алайық және оның контур бойымен қозғалу бағытын анықтайық.
Шынында да, DB түзуінен төмен орналасқан нүктелерде болады, өйткені шарттары орындалады. Олай болса өспелі функция болады, сондықтан DB түзуінен төмен орналасқан ағымдағы нүктесі осінің оң бағытында, содан оңға қарай қозғалуы тиіс.
ДВ түзуінен жоғары жатқан нүктелерде , өйткені , . Сондықтан функциясы кемитін болады, яғни ДВ түзуінен жоғары орналасқан нүктесі оңнан солға қарай қозғалады.
Сонымен біздің анықтағанымыз : кез келген контур бойындағы нүкте
t ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.