Ұңғымаларға және ұңғымалардың батареяларына сұйықтықтың ағу ерекшеліктері

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 24 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

«С. ӨТЕБАЕВ АТЫРАУ МҰНАЙ ЖӘНЕ ГАЗ УНИВЕРСИТЕТІ» КеАҚ

«Мұнайгаз» факультеті

КУРСТЫҚ ЖҰМЫС

«Мұнайдың жазық радиалды сүзілуі кезінде қоректену контурынан алыс орналасқан қабатта жұмыс істейтін ұңғымалар тобына сұйықтықтың құйылуын зерттеу»

(тақырыбы)

Мамандық коды және атауы «6В07203-Мұнай және газ кенорындарын игеру және пайдалану»

Топ Нгд 19/3

Орындаған: Зайдуллин Райымбек

(Т. А. Ә. )

Жетекші: Доцент, Каримова Ақмарал

(Т. А. Ә., ғылыми дәрежесі, атағы)

Атырау, 2021

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

«С. ӨТЕБАЕВ АТЫРАУ МҰНАЙ ЖӘНЕ ГАЗ УНИВЕРСИТЕТІ» КеАҚ

«Мұнайгаз» факультеті

«Бекітемін»

Факультет кеңесінің төрағасы

Ахметов Н. М. 2020 жылғы « »_ -дағы

№ хаттамасына сәйкес

ТАПСЫРМА

курстық жұмысқа арналған

Студент Зайдуллин Райымбек

Мамандығы 6В07203

Тобы Нгд 19/3

Тақырыбы «Мұнайдың жазық радиалды сүзілуі кезінде қоректену контурынан алыс орналасқан қабатта жұмыс істейтін ұңғымалар тобына сұйықтықтың құйылуын зерттеу»

№ факультет отырысында бекітілді « » 20 ж. бастап Жобаны (жұмысты) тапсыру уақыты « _» 20 ж. дейін Жобаны қорғау (жұмысты) : « » бастап «_ » 20 _ж. дейін

Жобаның (жұмыстың) бастапқы деректері

1.

2.

3.

4.

Негізгі бөлім Есептеу бөлімі

Ұсынылған әдебиеттер тізімі Сызбалық материалдар тізімі

(кестелер, диаграммалар, сызбалар және т. б. ) ;

Тапсырманы беру күні:« » 20 ж.

Жобаның (жұмыстың) жетекшісі:

Тапсырманы орындауға алдым: :« » 20 ж

Студент:

Мазмұны

Кіріспе

Кіріспе: Негізгі бөлім

: 1.

Кіріспе: Қорек контуры әртүрлі орналасқан ұңғымаларға сұйықтық ағыны

4: 4

: 1. 1.

Кіріспе: Қорек контуры қашық қаттағы ұңғымалар тобына сұйықтықтың түсуі

4: 4

: 1. 2.

Кіріспе: Қоректендірудің тік сызықты контуры бар қаттағы ұңғымаға сұйықтықтың түсуі

4: 7

: 1. 3.

Кіріспе: Тікелей сызықты өткізбейтін шекараның жанындағы резервуардағы ұңғымаға сұйықтықтың ағуы

4: 9

Кіріспе: Есептеу бөлімі

: 2.

Кіріспе: Ұңғымаларға және ұңғымалардың батареяларына сұйықтықтың ағу ерекшеліктері

4: 11

: 2. 1.

Кіріспе: Дөңгелек қабатта орналасқан ұңғымаға сұйықтық ағыны

4: 11

: 2. 2.

Кіріспе: Ұңғымалардың шексіз тізбектері мен сақиналы батареяларына сұйықтықтың ағуы

4: 13

: 2. 3.

Кіріспе: Жетілмеген ұңғымаларға сұйықтық пен газдың ағуы

4: 18

: 3.

Кіріспе: Сұйықтық пен газ шығынын өлшеуге арналған аспаптар

4: 20

: 3. 1.

Кіріспе: Басқарылатын пакері бар дебитомерлер

4: 21

: 3. 2.

Кіріспе: Кешенді аспаптар

4: 25

: 3. 3.

Кіріспе: Кәсіпшілік зерттеулердің міндеттері

4: 29

Кіріспе: Қорытынды

4: 31

Кіріспе: Пайдаланылған әдебиеттер тізімі

4: 32

Кіріспе

Нақты мұнай-газ кен орындары бірнеше ұңғымалармен игеріледі. Олардың саны көмірсутек шикізаты кен орнынан берілген іріктеуді қамтамасыз ету шартымен айқындалады. Сондықтан, кен орындарын игеруге байланысты сүзу есептеулерінде мұнай-газ аймағында белгілі бір жолмен орналастырылған көптеген Ұңғымаларды қарастыру қажет. Бұл жағдайда ұңғымалардың түбіндегі қысымды анықтау үшін гидродинамикалық тапсырмалар пайда болады, немесе, керісінше, берілген қысымдардағы дебиттер.

Осы мәселелерді шешу кезінде бірнеше ұңғымалардың жұмысы кезінде олардың бір - біріне өзара әсері-ұңғымалардың кедергісі болатындығын ескеру қажет. Бұл әсер жаңа ұңғымаларды іске қосу кезінде кен орнындағы жалпы өндіріс ұңғымалар санына қарағанда баяу өсетініне әкеледі.

Сондықтан, көмірсутекті шикізат кен орындарында болып жатқан процестерді неғұрлым барабар сипаттау мақсатында міндеттерді қиындата отырып, бір мезгілде бір емес, ұңғымалар топтары жұмыс істеген кезде міндеттерді қою мен шешуді қарастыру қажет. Тапсырмалардың ең қарапайым тұжырымдары резервуар тегіс деп есептелген кезде алынады, ал ұңғымалар дәл көздер немесе ағындар болып саналады. Мұндай мәселелерді шешуде тек жерасты гидромеханикасында ғана емес, сонымен қатар гидромеханиканың басқа бөлімдерінде ағынның потенциалы туралы болжам және суперпозиция әдісі (потенциал) кеңінен қолданылады.

Қорек контуры әртүрлі орналасқан ұңғымаларға сұйықтық ағыныҚорек контуры қашық қаттағы ұңғымалар тобына сұйықтықтың түсуі

Суперпозиция принципін қолдана отырып, зарядты, кенжар потенциалын (қысым), сүзу жылдамдығын және т. б. қуат тізбегі жойылған резервуарда жұмыс істейтін ұңғымалар тобы үшін есептейміз.

П ұңғымалары болсын (сурет. 1. 1) ФГ потенциалдары берілген (рсі кенжарлық қысымы), сондай - ақ RK қоректендіру контурының радиусы және ондағы Фк(ҚР контурлық қысымы) әлеуеті берілген г сі радиустарымен ұңғымалар арасындағы барлық арақашықтық та белгілі, rij-i-ші және j-ші ұңғымалар арасындағы арақашықтық. Qi ұңғымаларының (ағындарының) дебитін анықтау қажет.

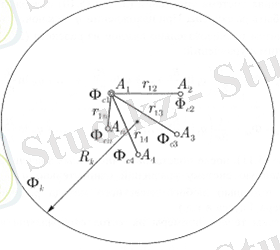
Сур. 1. 1. Қуаттандыру тізбегі қашық ұңғымалар тобының схемасы.

M еркін нүктесіндегі потенциал өрнегі (7. 5) формуласымен берілген. М нүктесін әр ұңғыманың түбіне қойып, p теңдеулерін аламыз:

(1. 1)

n+1 белгісіз: qi (i=1, 2, . . . , n) және С. сондықтан теңдеулер жүйесін жабу үшін М нүктесін қуат тізбегіне орналастырған кезде алынған тағы біреуін қосыңыз:

(1. 2)

Алынған теңдеулер жүйесі (1. 1) және (1. 2) n+1 теңдеуін қамтиды және оны шешуге болады. Ол үшін теңдіктердің әрқайсысын (1. 1) теңдіктен (1. 2) дәйекті түрде алып тастаймыз және N теңдеулерін аламыз:

(1. 3)

мұндағы Фк - қуат тізбегіндегі потенциал,

Ұңғыма қабырғаларындағы Фс-потенциал,

Q-дебит,

RK-қуат контурының радиусы,

RC-ұңғыма радиусы,

С-интегралдау тұрақтысы.

1. 2. Қоректендірудің тік сызықты контуры бар қаттағы ұңғымаға сұйықтықтың түсуі

Жұмыс ұңғымасы тікелей электр тізбегі бар резервуарда болсын, яғни резервуар-бұл шекара арқылы ұңғымаға ағып жатқан жартылай жазықтық. Ұңғымадан қуат тізбегіне дейінгі қашықтық А-ға тең, Вк қуат тізбегінде және Фс ұңғымасында потенциалдар берілген (сурет. 1. 2. ) . Ұңғыманың дебитін және резервуардың кез келген нүктесіндегі потенциалды анықтау қажет. Бұл жағдайда нақты ұңғыма тікелей электр тізбегіне қатысты айна түрінде көрсетіледі, көрсетілген ұңғыманың дебетіне нақты ұңғымадағы дебит белгісіне қатысты кері белгі қосылады. Қайнар көзі мен ағымының бұл орналасуы тұрақты потенциал берілген шекараны модельдеуге мүмкіндік береді.

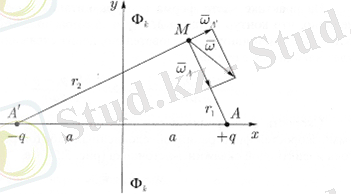
Сур. 1. 2. Тікелей электр тізбегіне жақын жұмыс істейтін ұңғымаға сұйықтықтың ағу схемасы.

М-нің еркін нүктесі үшін потенциалды жазамыз

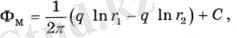(1. 4)

содан кейін біз м нүктесін алдымен нақты ұңғыманың қабырғасына, содан кейін қуат тізбегіне орналастырамыз және қуат көзі мен ағыннан қуат тізбегіндегі кез-келген нүктеге дейінгі қашықтық тең болатындығын қолданамыз, оны GC арқылы белгілейміз. Нәтижесінде теңдеулер жүйесін аламыз

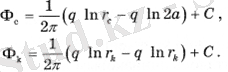(1. 5)

Q-ге қатысты алынған теңдеулер жүйесін шеше отырып, біз

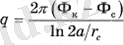(1. 6)

Соңғы формуланы потенциал үшін өрнекті қолдана отырып түрлендіруге болады,

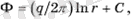(1. 7)

Нәтижесінде біз аламыз

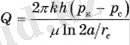(1. 8)

Ұңғыманың шығуы табылғаннан кейін, резервуардың кез келген нүктесінде потенциалды анықтауға болады

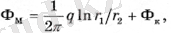(1. 9)

Егер қуат тізбегі шеңбер, а радиусы болса, онда дебит Дюпю формуласымен анықталады

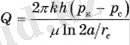(1. 10)

мұндағы Фк - қуат тізбегіндегі потенциал,

Ұңғыма қабырғаларындағы Фс-потенциал,

Q-дебит,

RK-қуат контурының радиусы,

RC-ұңғыма радиусы,

С-интегралдау тұрақтысы,

k-өткізгіштік коэффициенті,

h-контурдың қуаты (биіктігі),

µ-судың тұтқырлығы.

1. 3. Тікелей сызықты өткізбейтін шекараның жанындағы резервуардағы ұңғымаға сұйықтықтың ағуы.

Жұмыс ұңғымасы өткізбейтін шекарасы бар резервуарда болсын, яғни қабат жартылай жазықтықты білдіреді. Арақашықтық дейін ұңғыма өткізбеушілік қасиеті шекаралары сияқты а, қойған әлеуеті контурындағы тамақтану Шқ және ұңғымада Фс, контурдың радиусы тамақтану Rk (сур. 1. 3. ) . Ұңғыманың дебитін анықтау қажет. Іс жүзінде мұндай міндет тау-кен ұңғымасы төгіндіге немесе өнімді резервуардың сыналу шекарасына жақын орналасқан жағдайда пайда болуы мүмкін. Бұл жағдайда нақты ұңғыма өткізбейтін шекараға қатысты айна түрінде көрсетіледі, ал көрсетілген ұңғыманың дебеті нақты ұңғымамен бірдей белгіге жатады.

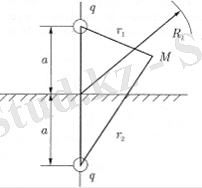
Сур. 1. 3. Тік сызықты өткізбейтін шекараның жанында жұмыс істейтін ұңғымаға сұйықтықтың ағу схемасы.

Содан кейін m еркін нүктесіндегі потенциал формула бойынша анықталады

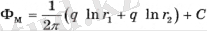(1. 11)

М нүктесін алдымен ұңғыманың қабырғасына, содан кейін қуат тізбегіне қойыңыз. Нәтижесінде біз аламыз

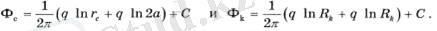(1. 12)

Бұл жағдайда RK >> а деп болжанады. q-ге қатысты алынған теңдеулер жүйесін шеше отырып, бізде

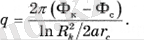(1. 13)

Потенциал үшін өрнектерді қолдана отырып, соңғы формуланы келесі түрде жазуға болады

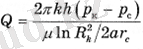(1. 14)

Ұңғымаларға және ұңғымалардың батареяларына сұйықтықтың ағу ерекшеліктеріДөңгелек қабатта орналасқан ұңғымаға сұйықтық ағыны

Жұмыс ұңғымасы дөңгелек қуат тізбегі бар резервуарда болсын, бірақ шеңбердің ортасынан S қашықтықта орналасқан (сурет. 2. 1. ) . Резервуардың ортасынан қуат тізбегіне дейінгі қашықтық Rk - ге тең, Вк қуат тізбегінде және Фс ұңғымасында потенциалдар берілген. Ұңғыманың дебитін және резервуардың кез келген нүктесіндегі потенциалды анықтау қажет. Бұл жағдайда, алдыңғы ұңғымадағыдай, нақты ұңғыма-а ағыны жалған ұңғымаға-а ұңғымасынан а қашықтықта орналасқан және ОА сәулесінде орналасқан А көзін көрсетеміз. А қашықтықты тізбектегі потенциалдың тұрақтылық жағдайынан және, демек, қуат тізбегінде орналасқан М1 және М2 нүктелерінен анықтаймыз.

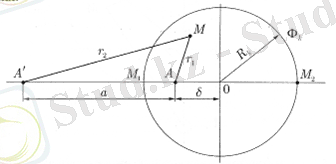
Сур. 2. 1. Дөңгелек қабатта эксцентрлік орналасқан ұңғымаға сұйықтықтың ағу схемасы.

M1 және M2 нүктелеріндегі потенциалдар үшін суперпозиция әдісіне сәйкес бізде келесі өрнектер бар:

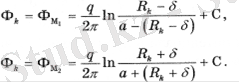(2. 1)

М1 және М2 нүктелеріндегі потенциалдар теңдігі шартынан а анықтау үшін теңдеулер аламыз

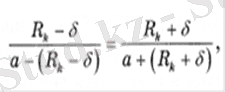
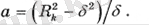(2. 2)

А ұңғымасының дебитін анықтау үшін оның кенжарындағы әлеуетті анықтаймыз

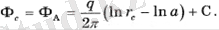(2. 3)

Бірінші теңдіктен (2. 1) (2. 3) қатынасын алып тастасақ, аламыз

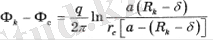(2. 4)

немесе а орнына оның өрнегін ауыстыру (2. 2)

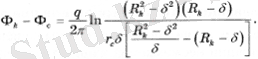(2. 5)

Соңғы теңдікте логарифм белгісінің астындағы өрнекті түрлендіріп, оны q-ге қатысты шеше отырып, дөңгелек қабатта эксцентрлік орналасқан ұңғыманың шығуы үшін формуланы табамыз:

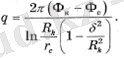(2. 6)

Егер эксцентриктілік нөлге тең болса (δ = 0), онда формула (4. 6) Дюпю формуласына айналады.

Резервуардың барлық нүктелерінде потенциалды табу үшін біз суперпозиция әдісін қолданамыз және М-нің еркін нүктесінде потенциалды жазамыз.

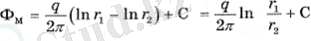(2. 7)

2. 2. Ұңғымалардың шексіз тізбектері мен сақиналы батареяларына сұйықтықтың ағуы

Бұл есептеулер үшін Ю. П. Борисов ұсынған балама сүзгілеу кедергісі әдісі қолданылады. Бұл әдіс кеуекті ортадағы сұйықтықтың қозғалысы мен сымдардағы электр тогының ағымы арасындағы ұқсастыққа негізделген.

Бір-бірінен 2 σ қашықтықта және тікелей электр тізбегінен L қашықтықта орналасқан ұңғымалардың бір шексіз тізбегіне сұйықтықтың ағуы туралы мәселені шешпей қарастырайық. Қуат тізбегінде потенциал FC - ге, ал ұңғымалардың қабырғаларында-FS-ге тең деп есептейміз (сурет. 5. 1) .

Әрбір ұңғыманың дебитін және тізбектегі N ұңғымаларының жалпы дебитін анықтау қажет.

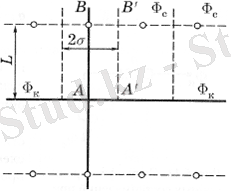
Сур. 2. 2. Ұңғымалардың тік сызықты тізбегінің схемасы.

Шешім міндеттері орналасқан әдісінің көмегімен суперпозиция. Ағынды ұңғымалар тізбегі ұңғымалардағы қуат тізбегіне қатысты айна түрінде көрінеді және шексіз резервуардағы екі ұңғыма тізбегінің кедергісі қарастырылады. Ұңғыма-ағын және ұңғыманың көзі арқылы өтетін АВ түзуінің бойымен бөлшектер ең жылдам қозғалады, ал ұңғымалар арасындағы қашықтықты жартысына бөлетін а' В ' түзулерінің бойымен қозғалыс ең баяу болады, өйткені ағынның симметриясына байланысты сызықтар өткізбейтін шекаралар болып табылады.

Әрбір ұңғыманың дебиті келесі формуламен анықталады:

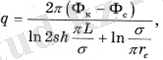(2. 8)

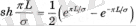-гиперболалық синус. L > σ болған жағдайда, E-πL / σ мәні аз болады, сондықтан l > σ кезінде ұңғымалардың дебитін формула бойынша есептеуге болады

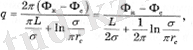(2. 9)

немесе, егер сіз белгіні енгізсек

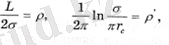(2. 10)

формуланы (2. 9) келесі түрде қайта жазуға болады.

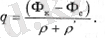(2. 11)

(2. 11) қатынасы ОМ Заңына ұқсас, сондықтан Ю. П. Борисов p мәнін батареяның сыртқы сүзгілеу кедергісі, ал p' - Ішкі деп атауды ұсынды. Осылайша, ұңғымалар тізбегіне сұйықтықтың ағынын суретте көрсетілген эквивалентті сүзгілеу кедергілерінің тізбегі ретінде көрсетуге болады. 2. 3.

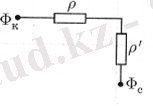
Сур. 2. 3. Ұңғымалардың шексіз тізбегіне ағу кезіндегі сүзгілеу кедергілерінің схемасы

Q дебитінің аналогы-ток күші, ал сүзу потенциалының айырмашылығының аналогы - электрлік потенциалдар айырмасы. Тік сызықты тізбек ұңғымаларының N жиынтық дебиті мына формула бойынша анықталады.

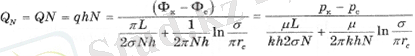(2. 12)

(2. 11) және (2. 12) формулаларды салыстырудан сыртқы сүзгілеу кедергісінің мәні өрнекпен анықталады

р = L / 2ahn, (2. 13)

ал ішкі

р' = = ln (σ/πrc) /2πhn. (2. 14)

Енді тік сызықты электр тізбегі бар жартылай шексіз қабатты сәйкесінше M1, m2 және m3 ұңғымаларының саны бар үш параллель ұңғымалар тізбегі Жасасын. Әрбір тізбектегі ұңғымалардың RC1, rc2, rc3 радиустары және рс1, рс2, рс3 кенжар қысымдары бірдей болсын, тізбектердің жалпы дебиттері Q'1, Q'2, Q'3 құрайды. (сур. 2. 4. )

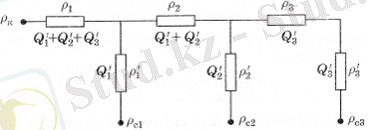
Сур. 2. 4. Ұңғымалардың үш тізбегіне ағу кезіндегі сүзгілеу кедергілерінің схемасы.

Схеманы есептеу ОМ және Кирхгоф заңдарына сәйкес электр тізбектерін есептеуге ұқсас. Сызықтық алгебралық теңдеулер Q'1, Q'2, Q'3 дебиттері үшін немесе рс1, рс2, рс3 кенжарлық қысымдары үшін не берілгеніне және нені анықтау керек екеніне байланысты жасалады. Бұл жағдайда сыртқы қарсылықтар теңдіктермен анықталады

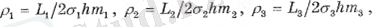(2. 15)

мұндағы L1, L2, L3-сәйкесінше қуат тізбегі мен бірінші тізбек арасындағы, бірінші және екінші тізбектер арасындағы және екінші және үшінші арасындағы қашықтық, егер мәселе потенциалдар теңдеулерінде шешілсе, және

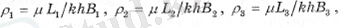(2. 16)

Ві=2σi, егер есеп теңдеулерде (2. 12) қысымдарды пайдалана отырып шешілсе, ішкі кедергі формулалармен анықталады

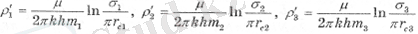(2. 17)

M ұңғымаларынан тұратын ұңғымалардың сақиналы батареясының бір ұңғымасының дебиті (сурет. 2. 5. ), RK радиусының дөңгелек қабатында

(2. 18)

мұндағы R1-ұңғымалар батареясының радиусы.

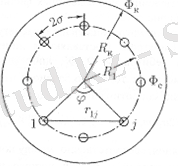
Сур. 2. 5. Ұңғымалардың сақиналы батареясының схемасы

Егер батареядағы ұңғымалардың саны 5-тен көп болса, онда (R1/Rk) 2M<<1 және формуланы (2. 18) жеңілдетуге болады, сонымен қатар егер R1/mrc=σ/πrc ауыстырылса, онда біз шамамен формуланы аламыз.

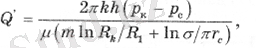(2. 19)

бұл жағдайда сыртқы және ішкі сүзгілеу кедергісі коэффициенттермен анықталады

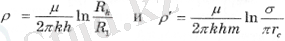(2. 20)

Екі сақиналы батарея болған жағдайда, қуат көзінің айналмалы контуры, ұңғымаларға ағу эквивалентті сүзгілеу кедергісі схемасына сәйкес есептеледі (сурет. 2. 6. ) .

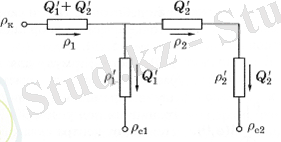
Сур. 2. 6. Ұңғымалардың екі сақиналы батареяларына ағу кезіндегі сүзгілеу кедергілерінің схемасы

Сыртқы және ішкі сүзгілеу кедергілері коэффициенттермен анықталады.

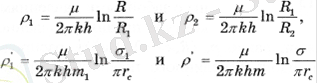(2. 21)

мұндағы R1, R2 - батареялардың радиусы, m1, m2 - батареядағы ұңғымалар саны.

Үш сақиналы батарея жағдайында, қуат көзінің айналмалы контуры, ұңғымаларға ағу 5. 3-суретте көрсетілген эквивалентті сүзгілеу кедергісі схемасы бойынша есептеледі. Сыртқы және ішкі сүзгілеу кедергілері коэффициенттермен анықталады.

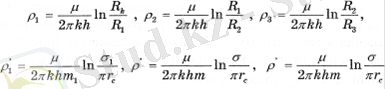(2. 22)

2. 3. Жетілмеген ұңғымаларға сұйықтық пен газдың ағуы

Соңғы қалыңдығы h қабатындағы ұңғыманың ашылу дәрежесі бойынша жетілмеген сұйықтыққа ағу міндетін М. Маскет зерттеді. Қабаттың төбесі мен табаны өткізбейтін болуы керек еді; ұңғыманың беткі қабаты да p=pc болатын эквипотенция болып табылады. Ұңғыманың осі бойымен в ұзындығының ашық бөлігінде әр элементі dz болатын сұйықтықты сіңіретін қиял сызығы болды. Абсорбциялық сызықтың ұзындығының бірлігіне келетін Q дебитінің қарқындылығы берілген шекаралық шарттарды орындау үшін әр түрлі нүктелерде таңдалды.

Тапсырма дисплей әдісімен шешілді, яғни. ұңғыма орналасқан сұйықтық ағыны идеалды сығымдалмайтындарға теңестіріліп, бірнеше ағынды суларға бөлінді. Көрсетілген шекаралық шарттарды орындау қабаттың төбесі мен табанына қатысты qdz қарапайым ағындарын сансыз рет көрсетуді қажет етті. Q дебитінің қарқындылығын таңдап, нақты және көрсетілген ағындардың суперпозиция әдісін қолдана отырып, М. Маскет резервуардың ашылу дәрежесінде жетілмеген ұңғыманың шығуы үшін келесі формуланы алды:

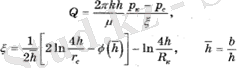(3. 1)

Функцияның аналитикалық өрнегі φ (h) :

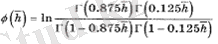(3. 2)

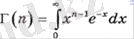(3. 3)

Өрнек (3. 3) - математикалық анықтамалықтарда кестелер бар гамма функциясы деп аталатын екінші типтегі Эйлер интегралы.

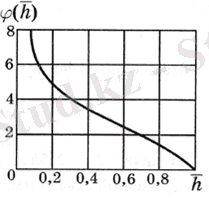
Сур. 3. 1. Φ (h) функциясының графигі

B=h жағдайында ұңғыма ашылу дәрежесі бойынша мінсіз болады, содан кейін оның дебиті Дюпю формуласына сәйкес болады.

Сұйықтық пен газ шығынын өлшеуге арналған аспаптар

Көп қабатты объектілерді әзірлеу кезінде оларды қабатпен зерттеу қажеттілігі туындайды, бұл әр қабат үшін сұйықтықтың ағынын немесе айдау ұңғымаларының қабаттарының қабылдағыштығын сандық бағалауға байланысты. Осы мақсатта өнімді қаттың қалыңдығы бойынша әртүрлі нүктелердегі сұйықтықтың (газдың) дебиттерінің (шығыстарының) мәндері туралы ақпарат алатын қашықтық аспаптар қолданылады. Ұңғыма шығынын өлшегіштердің көмегімен ұңғыма тоқтағаннан кейін сағалық және терең манометрлердің көрсеткіштері бойынша салынған қисыққа қарағанда, оған сұйықтықтың қосымша ағымының дәлірек қисығын алуға болады.

Ұңғымалардағы Сұйықтық пен газдың шығынын өлшеуге арналған құралдар шартты түрде ұңғымаға айдалатын су мен дымқыл будың шығынын өлшеуге арналған шығын өлшегіштерге және мұнай мен газдың шығынын анықтауға қызмет ететін дебит өлшегіштерге бөлінеді.

Ұңғымалардағы сұйықтық шығынын өлшеудің өзіндік ерекшеліктері бар, ең алдымен олар ұңғыманың ашық ұңғымасы немесе жұмыс бағанасы арқылы пайда болатын құбырларда жүзеге асырылады, олардың көлденең қимасы өлшеу орнында белгісіз. Сондықтан сұйықтық немесе газ ағынының жылдамдығын анықтаған кезде, ағынның жылдамдығын құбырдың көлденең қимасындағы жылдамдықтың көбейтіндісіне тең дәл өлшеу мүмкін емес. Сонымен қатар, терең снаряд құбырдың көлденең қимасы бойынша әртүрлі позицияларды алуы мүмкін және осыған байланысты, тіпті сол тереңдікте де бірдей болмайды.

Осыған байланысты тереңдік Шығын өлшегіштер (дебит өлшегіштер), әдетте, аспаптың калибрленген қимасы арқылы барлық өлшенген ағынды бағыттауға және ұңғыма оқпанындағы тереңдік снарядтың орнын орталықтандыруға арналған арнайы пакерлермен жабдықталған. Пакет ұңғымада бетінен басқарылатын қуат жетегі арқылы ашылады. Пакеттер ретінде сорғылардың көмегімен гидравликалық түрде ашылатын резеңке қабықшалар және ашылатын металл плиталар қолданылады.

Көптеген терең құрылғылардың сезімтал элементі турбина болып табылады. Іс жүзінде металл серіппелі пакеті бар терең турбиналық дебитомерлер кеңінен қолданылады.

Айдау ұңғымаларындағы су шығынын бақылау үшін орталықтандырғышы бар пакетсіз Шығыс өлшегіштер, сондай-ақ сусыз серіппелі пакеттік Шығыс өлшегіштер жиі қолданылады. Резеңке (абсолютті) қаптамасы бар Шығын өлшегіштер сирек қолданылады.

Басқарылатын пакері бар дебитомерлер

RGD-2M, RGD-36, Cobra-P36 және DGD қашықтықтан дебитомерлері негізінен өндіруші ұңғымаларды зерттеу үшін қолданылады: субұрқақтар мен сорғылар.

RGD-2M дебитомері турбиналық Шығыс сенсорнан және электр қозғалтқышы бар пакерлік құрылғыдан тұрады (сурет. 4. 1) Сұйықтық ағыны ағынды датчиктің корпусына пакермен жіберіледі және турбина 8 айналады, оның осінде магнит 7 күшейтіліп, герметикалық камерада орналасқан 6 магнитті басқарылатын контактімен өзара әрекеттеседі. Турбина айналған кезде байланыс электр тізбегін оның айналу жылдамдығына, демек, сұйықтықтың көлемдік ағынына пропорционал жиілікпен ашады және жабады.

Шығын өлшегіш пакет 1 Басқару блогы мен 2 тұрақты электр қозғалтқышының көмегімен ашылады. Қаптаманың жақтауы матадан немесе пленкадан жасалған қабықпен қапталған серіппелі таспалардан жасалған. Жабық күйде пакердің қабығы кіріс тесіктерін жабатын 9 құбырдың астында орналасқан. Қозғалтқыш 3 редукторы арқылы қосылған кезде, тығыздалған Білік 4 және 5 қозғағыштарын айналдырады. 9 құбыры жоғары қарай жылжиды және 11 диафрагмасы бар қуыс кесілген конус түрінде жасалған 13 серіппелі таспалардан және 12 манжеттерінен тұратын шам түріндегі пакерден алынады. Әрі қарай қозғалу кезінде құбыр 15 Крест және 10 тарту арқылы 14 жеңді көтереді, оған рамалық тақталар бекітіледі. Кезінде қысу пластиналарын пакер жабатын айналма алаңы және тұрған қабықшасына қарай жерге қағып орнатылған колоннаны құбырда. Сұйықтық кіріс терезелері арқылы турбина орнатылған калибрленген арнаға кіреді және құрылғыдан тесіктер арқылы шығады. Өлшеу жүргізілгеннен кейін пакер жабылады. Қозғалтқыштың реверсі кернеудің полярлығын өзгерту арқылы қамтамасыз етіледі.

Дебитомер "Кобра-Р36". Ондағы пакет жұқа жалпақ серіппелерден тұратын қуыс цилиндрлік пакет түрінде жасалады, олар қысылған кезде сақиналық саңылауды жабады. Мұндай дебитомерлердің ерекшелігі-кіріс және шығыс тесіктері өлшеу процесінде ғана ашылады. Бұл турбинаның жұмыс істеу ресурсын ұлғайтуға мүмкіндік береді және Түсіру-көтеру операциялары кезінде оны бітелуден қорғайды.

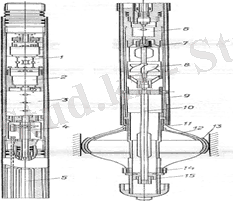
Сур. 4. 1. РГД-2м тереңдік дебитомері

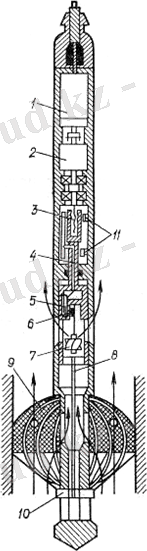
Сур. 4. 2. ДГД - 8 тереңдік дебитомері

ДГД типті дебитомерлер шағын диаметрлі лифтімен немесе шыныланған құбырлармен жабдықталған бұрқақты Ұңғымаларды зерттеуге арналған. Тереңдіктегі аспап корпусының диаметрі 26 мм ДГД-8 дебитомерін тереңдік-сорғы ұңғымаларының құбыр сыртындағы кеңістігіне түсіреді. Бұл құрылғыны тұтыну сенсоры (сурет. 11. 2) 6 тұрақты магниті бар 7 турбинадан және 5 магнитті басқарылатын түйіспеден тұрады. Пакер 9-бұл құрылғының диаметрінде орналасқан серіппелі таспаларды жабатын қабық. Қабықтағы өлшеудің жоғарғы шегін арттыру үшін тесіктер жасалуы мүмкін.

Пакет 7 Электр қозғалтқышының көмегімен ашылады, ол 2 редукторы арқылы жұмыс істейтін бұранданы 3 айналдырады және оған орналастырылған түрлендіргішпен 4 прогрессивті тығыздалған штанганы жылжытады. Бұл жағдайда 8 сырғытпасына қосылған 10 тарту сфералық пішінді алатын және сақиналық саңылауды жабатын серіппелі серіппелерді қысады. Электр қозғалтқышын қосу және ажырату үшін 11 шеткі микро ажыратқыштар арналған.