Қос қабатты потенциалдар түсінігі

МАЗМҰНЫ

Кіріспе

1. Потенциал түсінігінің теориялық әдістемелік негіздері

1. 1. Потенциал түсінігі түрлері

1. 2. Қос қабатты потенциалдар түсінігі

2. Қос қабатты потенциалдардың физикалық сипаттамасы

2. 1. Қос қабатты потенциалдардың қасиеттері

2. 2. Қос қабатты потенциалдардың математикалық үлгісі

Қорытынды

Пайдаланылған әдебиеттер тізімі

Кіріспе

Физика ғылымында потенциал түсінігі көптеген түсінікке ие. Кез келген адам электроникада немесе үй жағдайындағы электр желісінде потенциал өлшем бірлігі іспеттес.

Потенциал-физикалық күш өрістерінің кең көлемді тобын және физикалық шамалардың вектормен көрсетілген өрістерін сипаттайтын ұғым. Әрбір векторлық шама а өзінің потенциалының градиентіне тең: а=gradj. Мұндай жағдайда векторлық өрісті потенциалдық деп атайды. Потенциал векторлық өрісті сипаттау үшін көмекші функция ретінде енгізіледі. Термодинамикада потенциал берілген жүйе күйін сипаттаушы макропараметрлерге байланысты функция ретінде қарастырылады. Потенциал арқылы термодинамикалық жүйенің барлық қасиетін анықтауға болады. Физикада потенциал ұғымының басқа мағынасы да бар. Мысалы, электр өрісінде ол бірлік зарядты электр өрісінің берілген бір нүктесінен шексіздікке тасуға кеткен жұмысына тең.

Потенциал түсінігі күштің сапасы мен түрлі табиғаттың тізімінде де өте жақсы қолданылады. Скалярлық функция, мөлшерге орай вектор болады, бұл міне потенциал.

Гравитациялық потенциал өріске негізделген. Термодинамика процесінде потенциал түсінігі ішкі энергияның жүйесінде қолданылады. Ал механикада күшке негізделеді. Электрика саласында потенциал электрлік негізде. Электр өрісі электрлік потенциал. Статикалық формасныда электрлік потенциал энрегияда оң заряд береді, электромагниттік потенциалдың түрлі типтері анықталады. Оның екінші формасы векторлы, магнит өрісінде көрінеді.

Стандартты электродты потенциал мағынасы электродты реакция мүшелерінің активтілігіне байланысты емес және берілген электродқа қонстанта болады. 25 ⁰ С-ге қатысты стандартты потенциалдар (таблица өлшемдері) ; егер олар температуралық коэффициенттен, таблицадан табуға болады. Стандартты потенциалдар ерітінділердегі химиялық тепе-теңдікті есептеуге қолданылады. Стандартты электродты потенциалдардың астыңғы қатарында орналасқан кез-келген электрод қышқылдық түрде болады, үстіңгі қатардағы электродқа қарағанда (мысалы: Раниель - Якоб элементі) . Егер осындай электродтан электрохимиялық жүйе құрса, онда «астыңғы» реакция тотықтырғыш (Сu), ал «үстіңгі» - тотықсыздандырғыш реакция (Zn) . Бұл процесс химиялық жолмен өтетін және егер екі электродтың да белсенді заттары бір-бірімен қатынаста болып жүрсе, бұл реакция бір бағытта жүреді. Жүйеде тепе-теңдік орнайды, егер екі электрод потенциалы бірдей болса. Бұл реакция тепе-теңдік константасына байланысты жүреді.

1. Потенциал түсінігінің теориялық әдістемелік негіздері

1. 1. Потенциал түсінігі түрлері

Потенциал түсінігі кең түсінікке ие. Физикада потенциал термині әр түрлі өрістердің (электростатикалық, магниттік, гравитатциялық т. б. ) энергиясын сипаттау үшін қолданылатын шама. Биологиялық мембранада электр өрісі бар, олай болса ол өрістің энергиясын да осы тәрізді бипотенциал деген шамамен сипаттаймыз. Көбіне потенциалдың шамасын қолданбайды, олардың айырымын, яғни екі нүктедегі потенциалдар айрымын қолданады: Dj =j ₂ - j ₁ , мұндағы j ₂ и j ₁ сәйкес нүктелердегі (аймақтардағы) потенциал шамасы. Биопотенциал деп ағзаның екі нүке арасындағы потенциалдар айырымын немесе мембранадағы биопотенциал деп, мембрананың ішкі және сыртқы орта арасындағы потенциалдар айырымын атайды.

Электростатикалық өрістегі тасымалданатын заряд ретінде бірлік нүктелік оң зарядты алатын болсақ, нда 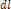жолдағы өріс күштерінің элементар жұмысы 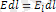-ге тең, мұндағы 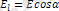- элементар орын ауыстыру бағытына Е векторының проекциясы.

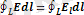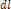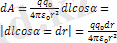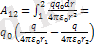Бұдан кернеулік векторының циркуляциясы деп аталады. Q нүктелік зарядтың өрісінде, зарядтың орын ауыстырғандағы істелетін жұмысын қарастырсақ, -жолдағы істелетін жұмысы . Кулон заңынан . Бұдан заряд потенциалы 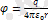екенін ескерсек 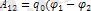) . Потенциал - скалярлық шама, өрістің берілген нүктесіндегі потенциалық энергияның, сыншы зарядқа қатынасы 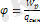. Бұдан потенциал өрістің энергетикалық сипаттамасын беретін физикалық шама екенін көреміз.

Электростатикалық өрістердің суперпозициялары принципінің көмегімен электр зарядтары жүйесі өрісінің кернеулігін есептеуді, еркін тұйық бетке толассыз электр өрісінің кернеулік векторының ағынын анықтауға болады. Q нүктелік зарядын қамтитын, r радиусын сфералық бетіне толассыз кернеулік веторының ағыны:
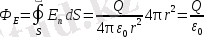
Бұл формула еркін тұйықталған бетке толассыз, вакуумдегі электростатикалық өрістің кернеулік векторының ағыны, 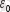ге бөлінген, зарядтардың осы бетінің ішіндегі алгебралық қосындыға тең.

Қозғалмайтын зарядтардың электр өрiсiн электростатикалық деп атайды. Ол тек электр зарядтарынан пайда болады және уақыт бойынша өзгермейдi. Электр өрiсi осы зарядтармен қоршаған кеңiстiкте бар болады және онымен үздiксiз байланыста болады. Электр диполiнiң негiзгi сипаттамасы диполь (электр) моментi деп аталатын векторлық физикалық шама болып табылады. Бұл моменттiң модулi заряд q модулiнiң арақашықтыққа L көбейтiндiсiне тең: . Сыртқы электростатикалық өріске орналасқан электрлік дипольдің энергиясын қарастырсақ. Алдымен сырты электростатикалық өрісте орналасқан екі дипольді аламыз. Олардың кернеулігі E1 және E2 тең. Ал потенциалы φ1 және φ2 тең деп аламыз. Сыртқы электростатикалық өріске орналасқан электрлік дипольдің энергиясы мынаған тең болады: U= -eφ1+eφ2=e{φ2- φ1}=e. δφ /δl. l=Pgradlφ, E=-gradφ, -gradlφ=El, U=pEl, U= -pEl=-(pE), p↑↑E.

Векторлық потенциал-құйынды векторлық өрісті сипаттауға арналып қолданылатын векторлық функция. Потенциал-физикалық күш өрістерінің кең көлемді тобын (электрлік, гравитатциялық, т. б. ) және физикалық шамалардың векторымен көрсетілген өрістерін(сұйықтық жылдамдығының өрісі, т. б. ) сипаттайтын ұғым. Әрбір векторлық шама а өзінің потенциалының градиентіне тең а=gradj. Мұндай жағдайда векторлық өрісті потенциялдық деп атайды. Векторлық өріс кестесінің әрбір нүктесінде вектор болатын функциямен сипаттайтын физикалық өріс.

Нүктелік зарядтар системасының потенциалын табу шін нүктелік заряд потенциалының формуласын және суперпозиция принципін пайдалану керек:𝜑= 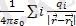. Мұндағы -потенциалы анықталып отырған нүктенің радиус-векторы, -i-ші нүктелік заряд орналасқан нүктенің радиус-векторы. Заряд белгілі бір көлем бойынша 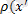, , 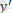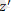) тығыздықпен үзіліссіз таралған болса, заряд таралған көлемнің әрбір бөлігін нүктелік заряд ретінде қарастыруға боларлықтай етіп өте кішкентай бөліктерге бөлеміз. 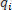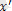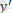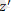Сонда әр бөлігінің заряды d =𝛒( , , ) d 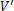болады. Енді суперпозиция бойынша және өте кішкентай көлемдер бойынша алынған қосындының шегі интегралға тең екенін ескерсек, 𝜑= 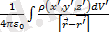болып шығады.

1. 2. Қос қабатты потенциалдар түсінігі

Қос қабатты потенциалдар түсінігінде электрлік қасиетіне байланысты барлық заттар полярлы молекула немесе полярлы емес болып бөлінеді. Молеуланың бірінші типінде жағымды және жағымсыз электр зарядтары кездеспейді, су молекуласына байланысты тиімді келеді. Полярлы молекула орталығында жағымды және қалыпты зарядтар кезігеді, олар азот қосылысында, сутегіде, бензолда, көміртегілерде кездеседі.

Молекула арасындағы әсер етулер ван дер вальсовты әсер етулермен анықталады. Ван дер вальс күшінің табиғаты электрлік молекулаға әсер етеді. Полярлы емес молеуланың әсері олардың арасында ғана болады. осындай типтегі молекуланың потенциалды энергиясы қос қабатты әсерлесуді құрайды. Ол мынадай болып өріледі:

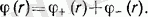
Заттың электрондық теориясы екінші құрастырушы молеулаларлдың арасындағы екінші тартуды құрайды. Молеула арасындағы тартылу күші, эмпирикалық тәуелсіздікте жазылады және де қос қабатты потенциал полярлы емес молекулаға әсерлеседі:

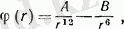
Мұнда тұрақты маңыздылық табылады, молеула құрылысында. Мұндай формадағы потенциал Леннард-Джонс потенциалына негізделген, оның потенциалының 6-12 сі деп аталады. Полярлы молекула үшін қосымша үшінші қабат ұсынылады, дипольды әсерлесу мен арақашықтығы бар, температураға да байланысты.

Оң потенциалды энергияда екі молекула арақашықтық арқылы өзгерісте болады, жағымды энергия тартылады. Графикалық маңыздылығы:

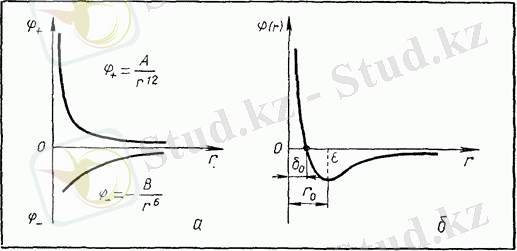
«Потенциальды шұқыр молекула арасында анықталады да екі параметрлі болады: терең және нолдік диаметрлі молекула. Бұл параметрлер химиялық табиғатта молекулаға сипатталады.

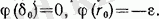
Қисық сызықтар және оське жақындау асимпты жақындау болады, яғни ол нолдік негізден басталғанда:

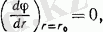
Бұл теңдікте тұрақты және потенциалдың басқа түрін алуға болады:

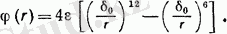
Молекула арасындағы әсер ету өндірістік потенциалға келеді:

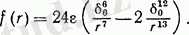
Күш арасындағы молекула аралық әсерлесу жағ, ымды болады, күштің оң әсер етуі беріледі. Тербеліс күші сығылады. Күштің сығылуын пайдалану арқылы жеңіл табуға болады:

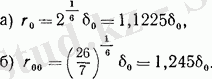
Тәуелділік негізіндегі процесте молекуланың жақындауы мен соқтығуы көрінеді. Молекуланың басталуы орталықтан басталады да, ал екінші молекула орталығында осьтік тиімсіздік пен кинетикалық энрегиядағы бастақы жазбаға бағытталады:

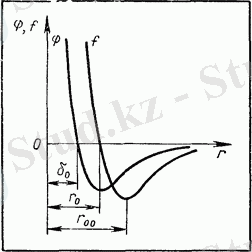
6. 13. сурет

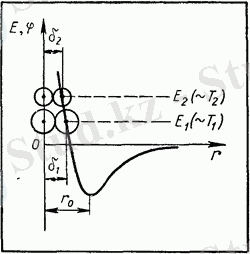
6. 14. сурет

Бірінші молекулаға жақындау, екінші күшті сығымдау жылдамдығы өсе түседі, ол үшін толық екі молекулалы энергия болады, сондықтан да ол өзгеріссіз қалады.

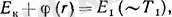
мұнда -жиілік массасы) .

2. Қос қабатты потенциалдардың физикалық сипаттамасы

2. 1. Қос қабатты потенциалдардың қасиеттері

Қос қабатты потенциалдардың көптеген қасиеттері бар. Жалпы дене электростатикалық өрісте потенциалдық энергияға ие, потенциалдық энергиялардын айырымы консервативті күштердің жұмысына тең. Сондықтан жұмысты зарядтардың потенциалдық энергияларының айырымы ретінде алуға болады.

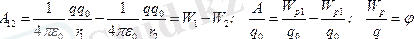
Біраттас зарядтар үшін потенциалдық әсерлесу энергиясы оң, әр аттас зарядтар потенциалдық әсерлесу энергиясы теріс. Электростатикалық өріс потенциалы қатынасы, зарядына байланысты емес, өрістің энергетикалық сипаттамасы . Потенциал скалярлық физикалық шама, бірлік оң зарядтың потенциалдық энергиясымен анықталады.

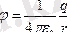
; зарядты 1-ші нүктеден 2-ші нүктеге орын ауыстырғандағы электростатикалық өріс күштерімен

, шексіз алыс нүктеде өріс жоқ.

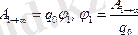
Бірінші нүктеде өріс потенциалы бірлік зарядты өріс бірінші нүктесінен шексіз алыс нүктеге дейін орын ауыстырганда жасалатын жұмысына тең.

. Нүктелік заряд потенциалы .

Егер өріс нүктелік зарядтар жуйесінен тудырса, онда зарядтын потенциалдық энергиясы, потенциалдық энергиялардын қосындысына тең.

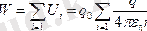
Қос қабатты потенциалдарда өріс болады, бір тракекториядан екінші траекторияға форма арқылы тәуелді болады. Потенциалдар ауырлық күші мен электростатикалық өріске негізделеді. Потенциалды өріс жұмысы теңдік негізде потенциалды энергия жүйесіне өзгеріспен қарама қарсы белгімен беріледі:

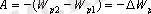
Потенциал - отношение потенциальной энергии заряда в поле к величине этого заряда:

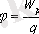
Тең болған біртекті өріс Потенциалы

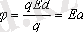
мұнда d - қашықтық, нол деңгейден басталған. 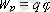теңдігі шығады.

Сондықтан да өріс жұмысы нүктенің φ ₁ потенциалы φ ₂ потенциалымен әрекеттеседі:

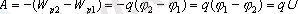
Мөлшер 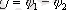потенциал деп аталады немесе қысым.

Қысым немесе түрлі потенциал екі нүкте арасына негізделеді бұл электрлік өрістің заряды мен мөлшерлі зарядтың бастапқы нүктесіндегі мөлшерген негізделген:

U=A/q

[U] =1Дж/Кл=1В

Егер де потенциалды энергия болмаса онда өрісте болмайды, оны шақыратын күште болмайды. Электр қызметі тиімді зарядталған бөлікте болады және де жағымды. Электрстатитикалық энергия түрлі белгілерді береді.

Потенциалды өзгертуді анықтауда оның нүктесі нолден басталады. Қалған маңыздары осы координатта болады. мысалы, электр техникада нолдік потенциал жердің бетінен алу анықталынған. Электростатикалық өрісте векторлық шама арқылы қысым мен скалярлы потенциалдың мөлшеріне негізделеді. Сондықтан да, олардың арасында анықталған байланыс бар. Егер де L траекториясының өндірістік жолында тиімсіз тесіктер кесілсе оны дифференциал деп қажет: dA = F * dL. Қысым-бұл мөлшер, пропорционал күште жылжымалы емес зарядта және қайтымды пропорциональда энергияның жиілікті маңызы табылады: E = F / q. Мұнда dA = Ei * q * dL. Электронға толық келетін күш Лоренц формуласына негізделген: F = qE + qV * B, мұнда B - магнитті индукция.

Өріс кернеулігі мен потенциаларасындағы байланыстың болуы электр күштерінің жұмысы кернеулік арқылы да өріс нүктерлерінің потенциалдар айырмасы арқылы да өрнектелетіндігінен байқалады. Кернеулік потенциалдың деңгей бетіне перпендикуляр болып келеді. Кернеулік оң зарядка әсер ететін күшпен бағыттас яғни потенциалдың кему жағына бағытталады. Кернеулік сан жағынан алғанда деңгей бетіне перпендикуляр жөнімен есептелген ұзындық бірлігіне келетін потенциалдың өзгерісіне тең болады да, потенциалдың кему жағына карай бағытталады. Потенциалдың деңгей бетіне перпендикуляр жөнімен оның өсу жағына карай орын ауыстырғанда потенциалдың өзгеру жылдамдығын көрсететін шама потенциал градиенті деп аталады. Кернеулік сан жағынан потенциал градиентіне тең. E= - Өрістің кернеулігі зарядталған жазықтықтар арасындағы нүктелердің бәрінде бірдей ж\е сол жазықтықтарға перпендикуляр болып келеді. Кернеуліктің сан мәнін деңгей беттерге перпендикуляр бағыттағы ұзындықтың бірлігіне келетін потенциалдың өзгерісі арқылы табамыз: E= 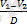кернеулік потенциалдың кему жағына карай бағытталған белгілі бір потенциалдары бар екі жазықтың арасындағы өрістің кернеулігі олардың потенциалдар айырмасына тура пропорционал ал олардың ара кашықтығына кері пропорционал. =-grad𝜑. - таңбасы өрістің кернеулігі әр уақытта, оның потенциалының кему бағытына қарай бағытталғандығын көрсетеді.

Қос қабатты потенциалдың мөлшері полярлы әсерлесу қатынасын береді. D* и Dq маңыздылығына ие.

мұнда D* - қос қабатты потенциалдың энергия мөлшері, потенциал шұқырынан пайда болған. Қос қабатты потенциалдың энергия мөлшері ролярлы әсерлесу қатынасын береді:

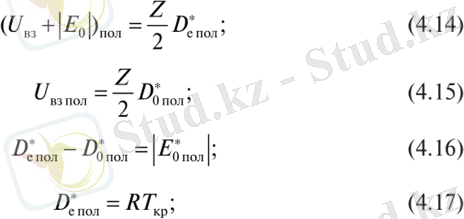
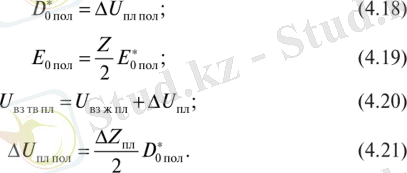
2. 2. Қос қабатты потенциалдардың математикалық үлгісі

Қос қабатты потенциалдар 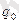зарядын 1-ші нүктеден 2-ші нүктеге көшіру үшін электростатикалық өрістің күштерінің жасайтын жұмысы мына түрде берілуі мүмкін.

яғни орын ауыстыратын зарядтың бастапқы және соңғы нүктедегі потенциалдар айырымына көбейтіндісіне тең. Электростатикалық өрістегі 1 және 2 екі нүктелердің потенциалдар айырымы бірлік оң зарядты 1 нүктеден 2-ші нүктеге орын ауыстырғандағы өріс күштерінің жасайтын жұмысымен анықталады.

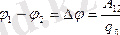
Электростатикалық өрістің кернеулігінің анықтамасын пайдаланып жұмысты мына түрде жаза аламыз.

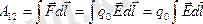
Осыдан

.

Электростатикалық өріс күшінің жұмысы орын ауыстыру траекториясына байланыссыз болғандықтан, мұндағы интегралдауды бастапқы және соңғы нүктелерді қосатын кез келген сызық бойымен алуға болады. Егер зарядын кез келген нүктеден өрістен тыс (шексіздікке) орын ауыстырсақ, онда потенциалдық энергия, олай болса потенциал нольге тең болады. Онда электростатикалық өріс күштерінің жұмысы

осыдан .

Сонымен, потенциалдың тағы бір анықтамасы шығады: потенциал дегеніміз бірлік оң зарядты берілген нүктеден шексіздікке орын ауыстырғандағы жұмыспен анықталатын физикалық шама. Жалпры потенциалдың өлшем бірлігі - вольт (В) ; 1В дегеніміз 1Кл заряд 1Дж потенциалдық энергияға ие болатын өрістің нүктесінің потенциалы (1В =1дж/1Кл) Егер өріс бірнеше зарядпен жасалса, онда зарядтар жүйенің өрісінің потенциалы осы зарядтардың өрістерінің потенциалдарының алгебралық қосындысына тең.

---

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс