Гравитациялық тұрақтылық

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 18 бет
Таңдаулыға:

ҒЫЛЫМИ ЖОБА
ГРАФИТАЦИЯЛЫҚ ТАРТЫЛЫС КҮШТЕРІ

Дайындаған:
Ғылыми жетекшісі:

2021-2022 оқу жылы
Ғылыми жобаның мазмұны
І. Кіріспе
ІІ. Негізгі бөлім
2.1 Бүкіләлемдік тартылыс заңы. Гравитациялық күштер
2.2 Гравитациялық тұрақтылық
2.3 Кеплер заңы
ІІІ. Зерттеу бөлімі
3.1 Бүкіләлемдік тартылыс заңы менің жеке тәжірибемде, есептер жинағы
ІҮ.Қортынды
Ү.Қолданылған әдебиеттер тізімі

Аннотация
Табиғаттағы күштердің бірі -- тартылыс күші. Ол кез келген денеге әрекет ете алады .Тартылыс күші өзара өзара тартымдылық ретінде көрінеді.Бүкіләлемдік тартылыс барлық денелердің бір-біріне дененің массасына және дене арасындағы қашықтыққа байланысты күшпен тартылатындығымен көрінеді. Тартылыс күші адам мен алма арасында да әрекет етеді , алайда оның мәнінің кішілігі соншалық, біз оны сезе алмаймыз. Тартылыс күшін анық сезу үшін денелердің бірі үлкен массаға ие болуы тиіс . Мысалы , Жердің массасы өте үлкен (6*1024 кг) , сондықтан ол Жерде жатқан барлық нәрселерді қатты тартады , ол мұхиттардағы суларды өзіне тартып , Айға ғарышқа ұшып кетуге жол бермейді .Ғылыми жобада графитациялық тартылыс күші кең көлемді тақырыпта, жан-жақты зерттеледі.

Аннотация
Одна из сил природы - гравитация. Он может воздействовать на любое тело. Гравитация рассматривается как взаимное притяжение. Вселенская гравитация проявляется в том, что все тела притягиваются друг к другу силой, зависящей от массы тела и расстояния между телами. Гравитация также действует между человеком и яблоком, но ее сущность настолько мала, что мы не можем ее почувствовать. Одно из тел должно иметь большую массу, чтобы отчетливо ощущать силу тяжести. Например, Земля имеет очень большую массу (6 * 1024 кг), поэтому она сильно притягивает все на Земле, что притягивает воду из океанов и мешает Луне улететь в космос. В исследовательском проекте сила тяжести подробно изучается по широкому кругу тем.

Аnnotation
One of the forces of nature is gravity. It can affect any body. Gravity is seen as mutual attraction. Universal gravity is manifested in the fact that all bodies are attracted to each other by a force that depends on the mass of the body and the distance between the bodies. Gravity also acts between a person and an apple, but its essence is so small that we cannot feel it. One of the bodies must have a large mass in order to clearly feel the force of gravity. For example, the Earth has a very large mass (6 * 1024 kg), so it strongly attracts everything on Earth, which attracts water from the oceans and prevents the Moon from flying into space. The research project explores gravity in detail across a wide range of topics.

Тақырыптың өзектілігі. Қазіргі теориялық физика Ньютонның гравитация заңымен басталғандығы жиі айтылады. Гравитация - табиғаттың негізгі күштерінің бірі. Ол астрономиялық құбылыстардың көбіне - мұхит толқындарынан бастап ғаламның кеңеюіне әкеледі. Ньютон қашықтықтың
квадратына кері пропорционалдылық туралы қарапайым заңмен ауырлықты сипаттады. Эйнштейн оны тереңірек көріп, ғарыштық уақытпен байланыстырды. Адамзат дамуында ғасырлар бойы адамдар денелерді өзара тартудың феноменін байқап, оның шамасын өлшеді; олар бұл тереңірек Әлемнің алғашқы қадамдарының барысында дәлдікпен санау, сайып келгенде, олардың қызметіне осы құбылысты қоюға өз ықпалын тигізді. Егер ауырлық болмаса, әлем қалай көрінетіні туралы ойлануға қызықты. Гравитация болмаса, Күн де, басқа жұлдыздар да, галактикалар сияқты үлкен жүйелер де өмір сүре алмайды. Бұл маңызды болуына қарамастан, гравитация әлі күнге дейін құпияда қалады. Сондықтан гравитацияға байланысты түрлі теорияларды сыни талдау әсіресе өзекті болып табылады. Шешілмеген мәселелер арасында гравитациялық толқындар проблемасы ғалымдар, теоретиктер мен экспериментаторлардың назарын аудартты. Гравитация тақырыбы басқа ғылымдармен тығыз байланысты, сондықтан оны теориялық және эксперименттік зерттеу көптеген ғылымдардың мәселелерін жеңілдетеді. Зерттеу мақсаттарына байланысты гравитациялық толқындардың теориялық сипаттамасы мәселесі, ең өзекті және қызықты, қазіргі заманғы физиканың бір бөлімі болды. (Осы мәселені бірінші 1916-1918 жылы Эйнштейн жүргізді.) Эйнштейн теориясы бір мезгілде дерлік пайда болмады, және бұл қазіргі уақытта әлі толық қанағаттанарлық шешімі жоқ. Соңғы он бес жылдан (шамамен 1957 жылдан бастап) астам уақытта оған қызығушылықтың артуына байланысты қуатты жаңа математикалық аппарат айтарлықтай өсті - Петровтың гравитациялық өріс классификациясын,теориялық тұрғысын ан проблемаларды жаңа тәсілдермен шешуге мүмкіндік берді. Екіншіден, соңғы жылдары қол жеткізген, эксперимент барысы, атап айтқанда, Вебердің тәжірибелері гравитациялық толқындарды зертханалық анықтау үшін мүмкіндік туғызды.

Мақсаты: бүкіләлемдік тартылыс заңының және гравитациялық тұрақтылықтың мәнін түсіну, оқыған теориялық мәліметтерді практикада қолдана білу

Ғылыми жұмыстың мақсатына жету үшін мына төмендегі міндеттерді шешуді қажет деп есептейміз:
+ бүкіләлемдік тартылыс заңының мәнін түсіну;
+ гравитациялық тұрақтылықтың физикалық мағынасын ашу;
+ гравитациялық тұрақтылық тақырыбы бойынша есептер жинақтау

І.Кіріспе
Гравитациялық тартылыс[[1]] - материяның кез келген түрлері арасындағы әмбебап өзара орекеттестік. Бұл әрекеттестік біршама әлсіз болса және денелер баяу жарықтың жылдамдығымен салыстырғанда) қoзғалыста болса, Ньютoнның бүкіләлемдік тартылыс заңына қамтылады.
Тартылыс күші адам мен алма арасында да әрекет етеді , алайда оның мәнінің кішілігі соншалық, біз оны сезе алмаймыз. Тартылыс күшін анық сезу үшін денелердің бірі үлкен массаға ие болуы тиіс . Мысалы , Жердің массасы өте үлкен (6*10[24] кг) , сондықтан ол Жерде жатқан барлық нәрселерді қатты тартады , ол мұхиттардағы суларды өзіне тартып , Айға ғарышқа ұшып кетуге жол бермейді .
Күн жүйесінде ең үлкен тартылыс күшін Күн тудырады , себебі оның массасы Жердің массасынан 300000 есе көп .
Табиғаттағы күштердің бірі -- тартылыс күші. Ол кез келген денеге әрекет ете алады .Тартылыс күші өзара өзара тартымдылық ретінде көрінеді.Бүкіләлемдік тартылыс барлық денелердің бір-біріне дененің массасына және дене арасындағы қашықтыққа байланысты күшпен тартылатындығымен көрінеді.
Ғылыми жобада графитациялық тартылыс кұшін зерттейтін боламын.

ІІ. Негізгі бөлім
2.1 Бүкіләлемдік тартылыс заңы. Гравитациялық күштер
Бүкіл әлемдік тартылыс заңы. Заңды И. Ньютон 1667 жылы ашты. 1665 жылы 23-жасында Ньютон Айды орбитада ұстап тұратын күш, Жерге алманың құлауына септігін тигізетін күш табиғатына ұқсас екендігін болжап айтты. Оның болжамы бойынша Әлемдегі барлық денелер арасында массалар центрін жалғастыратын түзу бойымен тартылыс (гравитациялық күштер) күштері әсер етеді.
Аңыз бойынша Ньютонға бүкіләлемдік тартылыс туралы ой, ол өз бағында демалып отырғанда құлаған алма себеп болған. Ньютонның аяғына дәл уақытында құлаған алманың ағашы елеусіз қалмай, оның бөлшектері Англияда осы уақытқа дейін сақталып келеді деген сөз бар.
Бүкіләлемдік тартылыс заңының ашылуы Ньютонға нақты математикалық дәлелдеулерге негізделген аспан денелерінің қозғалу теориясын жасауға мүмкіндік берді. Осыған дейін ғылымда мұндай жағдай болған емес. Бірақ бұл теорияның Ньютон замандастарына күшті әсері, оларды қанағаттанбағандық сезімінің пайда болуына кедергі бола алмады. Олар көптеген "неге?" - деген сұрақтарды қойды. Неге денелер тартылады? Ньютон бұл сұраққа жауап бермеді. "Тартылу күшінің қасиеттерінің себебін мен ғлі күнге құбылыстардан қорытып шығара алмадым, мен ойдан гипотеза шығармаймын деп жазды ол "Математикалық бастамаларда". Тартылыстың шынында бар екендігі және біз келтірген заңдармен әсер ететіндігі, сондай-ақ аспан денелерінің және теңіздің барлық қозғалыстарын түсіндіретіндігі жеткілікті".
Теңіз туралы айтқанда, Ньютон Ай мен Күннің суды тартуынан теңіздің тасу құбылысын меңзеп отыр. Ньютонға дейін бұл мәселемен екі жыл бұрын Аристотель айналысқан. Бірақ ол бұл мәселені шеше алмады. Аристотельге бұл мәселе қайғылы болды. "Негропонт жарқабағынан осы құбылысты бақылап отырып ол теңізге секіріп, өз еркімен ажал құшты" (Г. Галилей).
Ньютон онан кейінгі жылдары астроном И. Кеплердің XVII ғасыр басында ашқан ғаламшарлардың қозғалыс заңдылығының физикалық түсіндірмесін табуға тырысты және гравитациялық күштердің сан мәні қанша болатынын есептеді.Ғаламшарлардың қалай қозғалатынын біле отырып Ньютон оларға қандай күштер әсер ететіндігін анықтағысы келді. Бұл әдіс механиканың кері есебі деп аталады.
Ньютонның тартылыс заңы -- кез келген материялық бөлшектер арасындағы тартылыс күшінің шамасын анықтайтын заң. Ол И. Ньютонның 1666 ж. шыққан "Натурал философияның математикалық негіздері" деген еңбегінде баяндалған. Бұл заң былай тұжырымдалады: кез келген материялық екі бөлшек бір- біріне өздерінің массаларының (m1, m2) көбейтіндісіне тура пропорционал, ал ара қашықтығының квадратына (r2) кері пропорционал күшпен (F) тартылады: , мұндағы G -- гравитациялық тұрақты. Гравитациялық тұрақтының
(G) сан мәнін 1798 ж. ағылшын ғалымы Г. Кавендиш анықтаған. Қазіргі дерек бойынша G=6,6745(8)Һ Һ10 - 8см3гҺс2=6,6745(8)Һ
Һ10 - 11м3кгҺс2. Айдың Жерді, планеталардың Күнді айнала қозғалуын зерттеу нәтижесінде И. Ньютон ашқан бұл заң табиғаттағы барлық денелерге және олардың барлық бөліктеріне қолданылады. Б. ә. т. з. аспан денелерінің қозғалысы жайындағы ғылым -- аспан механикасының іргетасын қалайды. Осы заңның көмегімен аспан денелерінің қозғалу траекториясы есептелінеді және олардың аспан күмбезіндегі орындары алдын ала анықталады. Уран планетасының осы заңға сәйкес есептелінген орбитадан ауытқуы бойынша 1846 ж. Нептун планетасы ашылды.
Плутон планетасы да 1930 ж. осындай тәсілмен анықталды. 19 -- 20 ғ-ларда бұл заңды алдымен қос жұлдыздарға, сонан соң шалғай орналасқан галактикаларға да пайдалануға болатындығы белгілі болды. Жалпы салыстырмалық теориясының ашылуы (1916) нәтижесінде тартылыс күшінің табиғаты онан әрі айқындала түсті. Шындығында кез келген дене кеңістікте тартылыс өрісін туғызады. Денелердің арасындағы тартылыс күші осы өріс арқылы беріледі. Өте майда бөлшектерден тұратын микродүниедегі (атом, атом ядросы, элементар бөлшектер, т.б.) құбылыстарда Б. ә. т. з-ның әсері сезілмейді. Өйткені онда күшті, әлсіз және электр магниттік өзара әсерлер (қ. Әлсіз өзара әсер, Күшті өзара әсер, Электр магниттік өзара әсер) тәрізді өрістік әсерлер басым болып келеді.
Табиғаттағы барлық денелер бір-біріне тартылады. Осы тартылыс бағынатын заңды Ньютон анықтап, бүкіл әлемдік тартылыс заңы деп аталған.
Ньютон алғашында еркін құлау үдеуінің ара қашықтыққа тғуелділігін анықтады. Ол Жер бетінде, демек оның ортасынан 6400 км қашықтықта еркін түсу үдеуі 9,8 мс[2], ал 60 есе үлкен қашықтықтағы Айда: 3600 = 60[2]. Демек, еркін түсу үдеуі Жер ортасынан ара қашықтықтың квадратына кері пропорционал азаяды. Ньютонның екінші заңына сәйкес үдеу күшке пропорционал. ‡деудің осылай азаюы тартылу күшінің ара қашықтықтан тура сондай тғуелділігінен.
Тарту күшінің толық формуласын, бұл күштің әсерлесуші денелердің гравитациялық зарядтарына, демек олардың m1 және m2 массаларына пропорционал екендігін ескергенде анықтауға болады.
Ньютон Жердің оған тартылатын денелермен гравитациялық әсерлесу күшін анықтайтын өрнекті тапты. Өз интуициясына сенген ол анықталған формуламен өзара ара қашықтығымен r салыстырғанда өлшемі аз болатын Әлемдегі кез-келген денелер арасындағы тартылу күшін есептеуге болады деп ойлады. Сондықтан ол өзі анықтаған өрнекті аспан денелеріне де, Жер бетіндегі денелер үшін де дұрыс болатын бүкіләлемдік тартылыс заңы ретінде қарастырды. Ғылымның әрі қарай дамуы Ньютон заңының дұрыстығын, бұл заңды атомдар мен молекулалардан бастап керемет үлкен жұлдыздар шоғына да қолдануға болатындығын көрсетті.
Осы заң бойынша, екі дененің бір-біріне тартылатын күші осы денелердің массаларына тура пропорционал, ал олардың ара қашықтығының квадратына кері пропорционал болады:

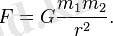
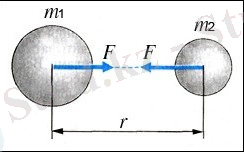
мұндағы, G - гравитациялық тұрақты деп аталатын пропорционалдық коэффициент. Бұл күш бір-біріне әсер ететін денелер арқылы өтетін түзудің бойымен бағытталған. Формула шамасы бойынша бір-біріне тең F12 және F21 күштердің сандық мәнін береді. Cуреттегі өзара әсерлесетін денелер біртекті шарлар болса, m1 және m2 - шар массалары, r - олардың центрінің ара қашықтығы. Сонымен, шарлар материялық нүктелер ретінде өзара әсерлеседі , ал олардың массалары шар массаларына тең және олардың центрлерінде орналасқан. Гравитациялық тұрақтының сандық мәні, массалары белгілі денелердің бір-біріне тартылатын күшін өлшеу жолымен анықталған. Осындай өлшеу кезінде көп қиыншылықтар кездеседі, өйткені массалары тікелей өлшенетін денелер үшін тартылыс күштері өте-мөте аз болып шығады. Мысалы, әрқайсысының массасы 100 кг, бір-бірінен қашықтығы 1 метр болатын екі дене бір-біріне шамамен 10[−6] Н, яғни 10[−4] Г күшпен өзара әсер етеді.
Механиканың негізгі есебі бойынша массасы мен жылдамдығы белгілі денеге әсер ететін күштің салдарынан кез келген уақыт мезетіндегі дененің орнын анықтау болса ,механиканың кері есебінде дененің қалай қозғалатындығына қарай оған әсер ететін күштерді анықтау болып табылады
Осы есепті шешу арқылы Ньютон бүкіл әлемдік тартылыс заңын ашты. Барлық денелер бір-біріне өздерінің массаларының көбейтіндісіне тура пропорционал және арақашықтығының квадратына кері пропорционал күшпен тартылады:
Пропорционалдық коэфициент G табиғаттағы барлық денелер үшін бірдей және оны бүкіл әлемдік тартылыс тұрақтысы немесе гравитациялық тұрақты деп атайды.
G = 6,67·10-11 Н·м2кг2 (СИ).
Табиғаттағы көптеген құбылыстар бүкіләлемдік тартылыс күшімен түсіндіріледі.
Күн жүйесіндегі ғаламшарлар қозғалысы,
жердің жасанды серігінің қозғалыстары , 3.баллистикалық зымырандардың ұшу траекториясы
4. Жерге жақын денелердің қозғалысы, 5.Денелердің жерге құлауы,
6.Тасу және қайту, 7.Сарқырамалар,
Қол сөмкесінің ауырлығы.
Жер атмосферасының болуы т.б құбылыстар динамика заңдарымен және бүкіләлемдік тартылыс заңы арқылы түсіндіріледі
Егер M - Жер массасы , RЗ - оның радиусы, m - берілген дене массасы болса , онда ауырлық күші
мұндағы g - Жер бетіндегі еркін түсу үдеуі.:
Бүкіләлемдік тартылыс заңының бір байқалуы ауырлық күші болып табылады.
Жер бетіне жақын денелердің тарту күшін осылай атау қабылданған
Ауырлық күші жер центріне қарай бағытталған.Басқа күштер болмағанда дене Жерге еркін түсу үдеуімен құлайды. Жердің әр түрлі нүктелеріндегі еркін түсу үдеуінің орташа мәні 9,81 мс2. Жердің радиусы мен еркін түсу үдеуінің мәнін біле отырып(Rз = 6,38·106 м), Жер массасын М есептеп шығаруға болады.:
Ауырлық күші жер центріне қарай бағытталған.Басқа күштер болмағанда дене Жерге еркін түсу үдеуімен құлайды. Жердің әр түрлі нүктелеріндегі еркін түсу үдеуінің орташа мәні 9,81 мс2. Жердің радиусы мен еркін түсу үдеуінің мәнін біле отырып(Rз = 6,38·106 м), Жер массасын М есептеп шығаруға болады.:
Жерден қашықтаған сайын Жердің тарту күші мен еркін түсу үдеуі Жер центріне дейінгі ара қашықтықтың квадратына кері пропорционал өзгереді. Жерден қашықтап бара жатырған ғарыш кемесінің ішіндегі ғарышкерге әсер ететін тартылыс күшінің өзгеруі бейнеленген. Жерге жақын маңда ғарышкерге әсер ететін тарту күші 700 Н-ғатең деп алсақ:
Жерден қашықтап бара жатырған ғарышкерге әсер ететін тарту күшінің өзгерісі.
Сонымен, Ньютон ашқан бүкіләлемдік тартылыс заңы былай тұжырымдалады:
Кез-келген екі бөлшектің гравитациялық тартылу күші олардың массаларының көбейтіндісіне тура пропорционал, ал олардың ара қашықтығының квадратына кері пропорционал. Бұл заң математикалық түрде формуламен өрнектеледі. Бұл формуладағы G - пропорционалдық коэфициенті гравитациялық тұрақты деп аталады. Бұл жерде бүкіләлемдік тартылыс заңы бөлшектер үшін,
демек, өлшемдері r ара қашықтығынан ғлдеқайда аз денелер үшін тұжырымдалған. Алайда бұл заңның керемет бір ерекшілігі оны басқа да жағдайларда қолдануға мүмкіндік береді. Тартылу күшінің бөлшектерден ара қашықтығының үшінші немесе төртінші дәрежесіне емес, тек квадратына тғуелділігі бұл заңның аталған ерекшілігі. Есептеулер көрсеткеніндей тура осыған байланысты - формуланы ішіндегі заты сфералық- симметриялы таралған шар тәрізді дғнелердің арасындағы ара қашықтықтың кез-келген мәні үшін қолдануға болады. Бұл жағдайды r -денелер арасындағы қашықтық емес, сол денелердің орталықтары арасындағы қашықтық. формула аралық жағдайда да дұрыс, мысалы өлшемі кез- келген сфералық дене материаялық нүктемен әсерлескенде. Осы жағдай бүкіләлемдік тартылу формуласын Жер шарының заттарды тарту күшін есептеуге мүмкіндік береді

2.2 Гравитациялық тұрақтылық
Табиғаттағы барлық денелер бір-біріне тартылады. Осы тартылыс бағынатын заңды Ньютон ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.